8.6: الأطياف الذرية والأشعة السينية
- Page ID
- 196723
في نهاية هذا القسم، ستكون قادرًا على:
- وصف امتصاص وانبعاث الإشعاع من حيث مستويات الطاقة الذرية واختلافات الطاقة
- استخدم الأرقام الكمومية لتقدير الطاقة والتردد والطول الموجي للفوتونات الناتجة عن التحولات الذرية في ذرات الإلكترونات المتعددة
- شرح مفاهيم الإشعاع في سياق الفلورة الذرية والأشعة السينية
توفر دراسة الأطياف الذرية معظم معرفتنا بالذرات. في العلوم الحديثة، تُستخدم الأطياف الذرية لتحديد أنواع الذرات في مجموعة من الأجسام، من المجرات البعيدة إلى عينات الدم في مسرح الجريمة.
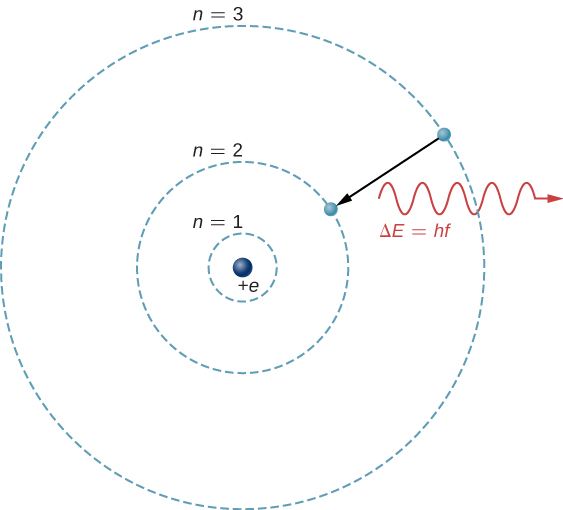
الأساس النظري للتحليل الطيفي الذري هو انتقال الإلكترونات بين مستويات الطاقة في الذرات. على سبيل المثال، إذا قام إلكترون في ذرة هيدروجين بالانتقال من الغلاف\(n = 3\) إلى\(n = 2\) الغلاف، فإن الذرة تصدر فوتون بطول موجة
\[\lambda = \frac{c}{f} = \frac{h \cdot c}{h \cdot f} = \frac{hc}{E_3 - E_2}, \nonumber \]
أين\(\Delta E = E_3 - E_2\) يتم نقل الطاقة بواسطة الفوتون و\(hc = 1240 \, eV \cdot nm\). بعد مرور هذا الإشعاع عبر مقياس الطيف، يظهر كخط طيفي حاد على الشاشة. يظهر نموذج Bohr لهذه العملية في الشكل\(\PageIndex{1}\). إذا امتص الإلكترون لاحقًا الفوتون بالطاقة\(\Delta E\)، يعود الإلكترون إلى\(n = 3\) الغلاف (قمنا بفحص نموذج Bohr سابقًا).
لفهم التحولات الذرية في ذرات الإلكترونات المتعددة، من الضروري النظر في العديد من التأثيرات، بما في ذلك تنافر كولوم بين الإلكترونات والتفاعلات المغناطيسية الداخلية (وصلات الدوران والمدار والدوران). لحسن الحظ، يمكن فهم العديد من خصائص هذه الأنظمة من خلال إهمال التفاعلات بين الإلكترونات وتمثيل كل إلكترون من خلال وظيفة الموجة أحادية الجسيم الخاصة به\(ψ_{nlm}\).
يجب أن تخضع التحولات الذرية لقواعد الاختيار. تنبع هذه القواعد من مبادئ ميكانيكا الكم والتماثل. تصنف قواعد التحديد الانتقالات على أنها مسموح بها أو محظورة. (تحدث الانتقالات المحرمة، ولكن احتمال الانتقال المعتاد المحظور صغير جدًا.) بالنسبة للذرة الشبيهة بالهيدروجين، تخضع التحولات الذرية التي تنطوي على تفاعلات كهرومغناطيسية (انبعاث وامتصاص الفوتونات) لقاعدة الاختيار التالية:
\[\Delta l = \pm 1, \label{select1} \]
حيث\(l\) يرتبط بحجم الزخم الزاوي المداري،
\[L = \sqrt{l(l + 1)}\hbar. \nonumber \]
بالنسبة للذرات متعددة الإلكترون، تنطبق قواعد مماثلة. لتوضيح هذه القاعدة، ضع في اعتبارك التحولات الذرية المرصودة في الهيدروجين (H) والصوديوم (Na) والزئبق (Hg) (الشكل\(\PageIndex{2}\)). تتوافق الخطوط الأفقية في هذا المخطط مع مستويات الطاقة الذرية، وتظهر التحولات التي تسمح بها قاعدة التحديد هذه بخطوط مرسومة بين هذه المستويات. وتتراوح طاقات هذه الحالات بين بضعة فولتات إلكترونية، وتقع الفوتونات المنبعثة في التحولات في النطاق المرئي. من الناحية الفنية، يمكن أن تنتهك التحولات الذرية قاعدة الاختيار، ولكن مثل هذه التحولات غير شائعة.
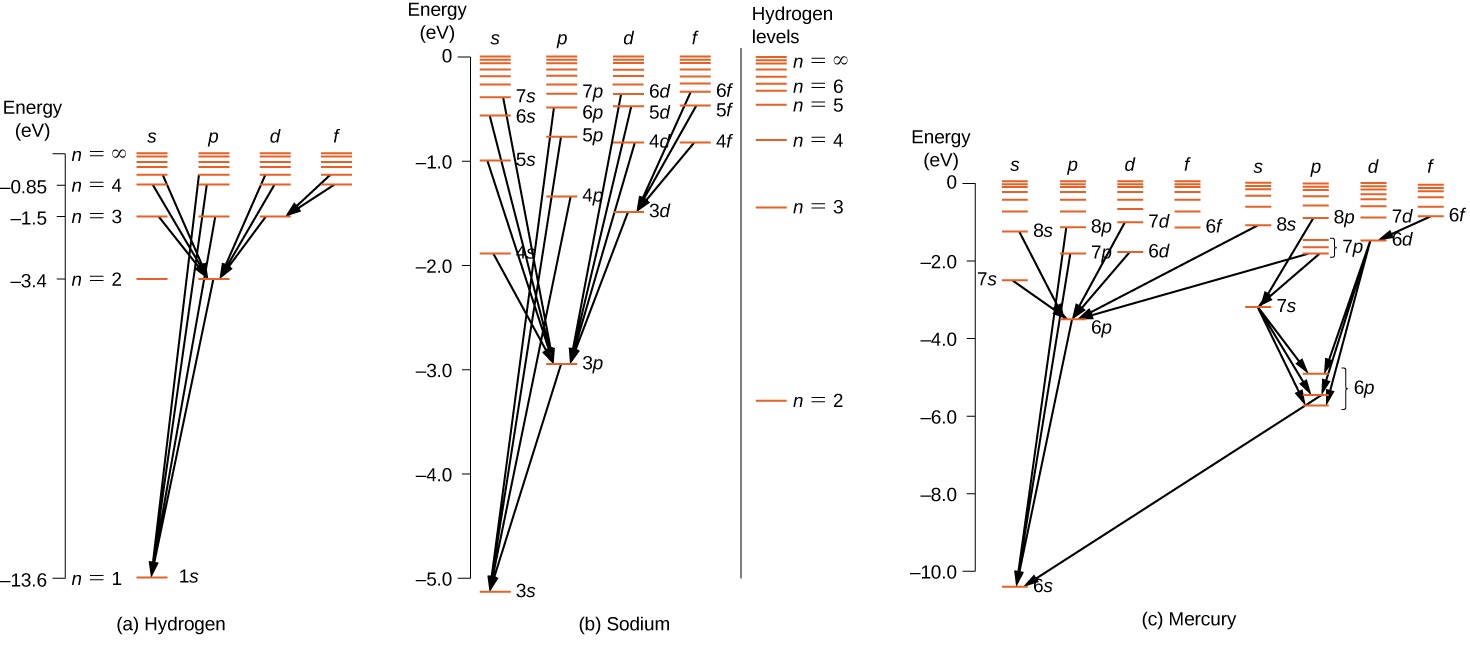
تحتوي ذرة الهيدروجين على أبسط رسم تخطيطي لمستوى الطاقة. إذا أهملنا دوران الإلكترون، فإن جميع الحالات التي لها نفس قيمة n لها نفس الطاقة الكلية. ومع ذلك، فإن الاقتران بين الدوران والمدار يقسم\(n = 2\) الحالات إلى حالتي زخم زاويتين (درجات و p) من الطاقات المختلفة قليلاً. (لا يتم إزاحة هذه المستويات عموديًا، لأن تقسيم الطاقة صغير جدًا بحيث لا يمكن ظهوره في هذا الرسم التخطيطي.) وبالمثل، يؤدي اقتران الدوران والمدار إلى تقسيم الحالات إلى ثلاث حالات زخم زاوي (s و p و d).\(n = 3\)
يشبه مخطط مستوى الطاقة للهيدروجين الصوديوم، لأن كلتا الذرتين تحتويان على إلكترون واحد في الغلاف الخارجي. يتحرك إلكترون التكافؤ الخاص بالصوديوم في المجال الكهربائي لنواة محمية بالإلكترونات في الأصداف الداخلية، لذلك لا يواجه جهدًا بسيطًا قدره 1/ r Coulomb وتعتمد طاقته الإجمالية على كل من n و l. ومن المثير للاهتمام أن الزئبق يحتوي على رسمين تخطيطيين منفصلين لمستوى الطاقة؛ وتتوافق هذه المخططات مع حالتي دوران صافيتين لإلكتروناته ذات الستة ثوانٍ (التكافؤ).
يتم تحليل طيف الصوديوم باستخدام مطياف. لوحظ وجود خطين متباعدين بأطوال موجية 589.00 نانومتر و 589.59 نانومتر.
- إذا كان الصمام المزدوج يتوافق مع الإلكترون المثير (التكافؤ) الذي ينتقل من حالة مُثارة إلى حالة ٣ ث، فما مقدار الزخم الزاوي للإلكترون الأصلي؟
- ما هو فرق الطاقة بين هاتين الحالتين المتحمستين؟
إستراتيجية
ينتمي الصوديوم والهيدروجين إلى نفس العمود أو المجموعة الكيميائية من الجدول الدوري، لذا فإن الصوديوم «يشبه الهيدروجين». يقع الإلكترون الخارجي في الصوديوم في الغلاف الفرعي 3 s (\(l=0\)) ويمكن تحفيزه لمستويات طاقة أعلى. بالنسبة للهيدروجين، يجب أن تخضع الانتقالات اللاحقة إلى مستويات الطاقة المنخفضة لقاعدة الاختيار (المعادلة\ ref {select1}):
\[\Delta l = \pm 1 \nonumber \]
يجب علينا أولاً تحديد الرقم الكمي للحالة الأولية التي تفي بقاعدة الاختيار. بعد ذلك، يمكننا استخدام هذا الرقم لتحديد حجم الزخم الزاوي المداري للحالة الأولية.
الحل
- يجب أن تخضع الانتقالات المسموح بها لقاعدة التحديد. إذا كان الرقم الكمي للحالة الأولية هو\(l = 0\)، فإن الانتقال محظور بسبب\(\Delta l = 0\). إذا كان الرقم الكمي للحالة الأولية هو\(l = 2,3,4,...\) أن الانتقال محظور بسبب\(\Delta l > 1\). لذلك، يجب أن يكون مقدار الحالة الأولية\(l=1\). الزخم الزاوي المداري للحالة الأولية هو\[L = \sqrt{l(l + 1)}\hbar = 1.41 \hbar. \nonumber \]
- نظرًا لأن الحالة النهائية لكلا الانتقالين هي نفسها (3 ثوان)، فإن الفرق في طاقات الفوتونات يساوي الفرق في طاقات الحالتين المتحمستين. باستخدام المعادلة\[\Delta e = hf = h\left(\frac{c}{\lambda}\right), \nonumber \] التي لدينا\[\begin{align*} E &= hc\left(\frac{1}{\lambda_1} - \frac{1}{\lambda_2}\right) \\[4pt] &=(4.14 \times 10^{-15} eVs)(3.00 \times 10^8 m/s) \times \left(\frac{1}{589.00 \times 10^{-9} m} - \frac{1}{589.59 \times 10^{-9} m}\right) \\[4pt] &= 2.11 \times 10^{-3} eV. \end{align*} \nonumber \]
الدلالة
لفهم صعوبة قياس فرق الطاقة هذا، نقارن هذا الاختلاف بمتوسط طاقة الفوتونين المنبعثين في المرحلة الانتقالية. إذا كان متوسط طول الموجة 589.30 nm، فإن متوسط طاقة الفوتونات هو
\[E = \frac{hc}{\lambda} = \frac{(4.14 \times 10^{-15} eVs) (3.00 \times 10^8 m/s)}{589.30 \times 10^{-9} m} = 2.11 \, eV. \nonumber \]
يبلغ فرق الطاقة\(\Delta E\) حوالي 0.1٪ (جزء واحد في 1000) من متوسط الطاقة هذا. ومع ذلك، يمكن لمقياس الطيف الحساس قياس الفرق.
الفلورسينية الذرية
يحدث التألق عندما يتم تحفيز إلكترون في الذرة بعدة خطوات فوق الحالة الأرضية عن طريق امتصاص الفوتون فوق البنفسجي عالي الطاقة (UV). بمجرد الإثارة، «يزيل الإلكترون الإثارة» بطريقتين. يمكن للإلكترون العودة إلى الحالة الأرضية، حيث ينبعث منه فوتون من نفس الطاقة التي أثارتها، أو يمكن أن ينخفض في سلسلة من الخطوات الصغيرة، وينبعث منه عدة فوتونات منخفضة الطاقة. قد تكون بعض هذه الفوتونات في النطاق المرئي. يمكن للصبغة الفلورية في الملابس أن تجعل الألوان تبدو أكثر إشراقًا في ضوء الشمس عن طريق تحويل الأشعة فوق البنفسجية إلى ضوء مرئي. تعتبر مصابيح الفلورسنت أكثر كفاءة في تحويل الطاقة الكهربائية إلى ضوء مرئي من الشعيرات المتوهجة (حوالي أربعة أضعاف الكفاءة). \(\PageIndex{3}\)يُظهر الشكل عقرب مضاء بمصباح الأشعة فوق البنفسجية. تصدر البروتينات القريبة من سطح الجلد ضوءًا أزرقًا مميزًا.

الأشعة السينية
تمكننا دراسة تحولات الطاقة الذرية من فهم الأشعة السينية وتكنولوجيا الأشعة السينية. مثل كل الإشعاع الكهرومغناطيسي، فإن الأشعة السينية مصنوعة من الفوتونات. يتم إنتاج فوتونات الأشعة السينية عندما تنخفض الإلكترونات الموجودة في الأصداف الخارجية للذرة إلى الأصداف الداخلية. (لا تصدر ذرات الهيدروجين أشعة سينية، لأن مستويات طاقة الإلكترون متباعدة جدًا معًا للسماح بانبعاث إشعاع عالي التردد.) عادةً ما يتم حظر الانتقالات من هذا النوع لأن الولايات الدنيا ممتلئة بالفعل. ومع ذلك، إذا كان هناك فراغ في الغلاف الداخلي (الإلكترون الداخلي مفقود، ربما بسبب تعرضه للإلكترون عالي السرعة)، يمكن للإلكترون من أحد الأغلفة الخارجية أن ينخفض طاقته لملء الفراغ. فجوة الطاقة لمثل هذا الانتقال كبيرة نسبيًا، لذا فإن الطول الموجي لفوتون الأشعة السينية المشع قصير نسبيًا.
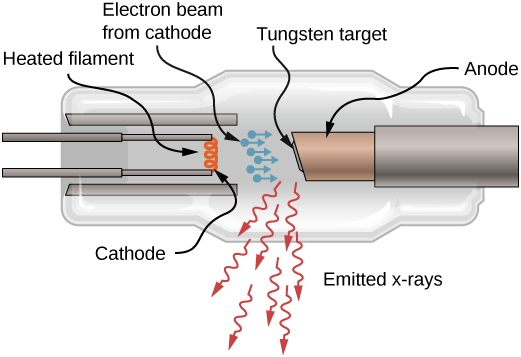
يمكن أيضًا إنتاج الأشعة السينية عن طريق قصف هدف معدني بإلكترونات عالية الطاقة، كما هو موضح في الشكل\(\PageIndex{4}\). في الشكل، يتم غلي الإلكترونات من الفتيل ويتم تسريعها بواسطة مجال كهربائي إلى هدف التنغستن. وفقًا للنظرية الكلاسيكية للكهرومغناطيسية، فإن أي جسيم مشحون يسرع يصدر إشعاعًا. وهكذا، عندما يضرب الإلكترون هدف التنغستن، ويتباطأ فجأة، يصدر الإلكترون إشعاع الكبح (غالبًا ما يستخدم المصطلح باللغة الألمانية: Bremsstrahlung). يشير إشعاع الكبح إلى الإشعاع الناتج عن أي جسيم مشحون يتباطأ بواسطة وسيط. في هذه الحالة، يحتوي إشعاع الكبح على نطاق مستمر من الترددات، لأن الإلكترونات سوف تصطدم بالذرات المستهدفة بطرق مختلفة قليلاً.
إشعاع الكبح ليس النوع الوحيد من الإشعاع الناتج عن هذا التفاعل. في بعض الحالات، يصطدم الإلكترون بإلكترون آخر ذو غلاف داخلي للذرة المستهدفة، ويخرج الإلكترون من الذرة - بأسلوب كرة البلياردو. يتم ملء الحالة الفارغة عندما ينخفض إلكترون في غلاف أعلى إلى الحالة (انخفاض مستوى الطاقة) وينبعث منه فوتون بالأشعة السينية.
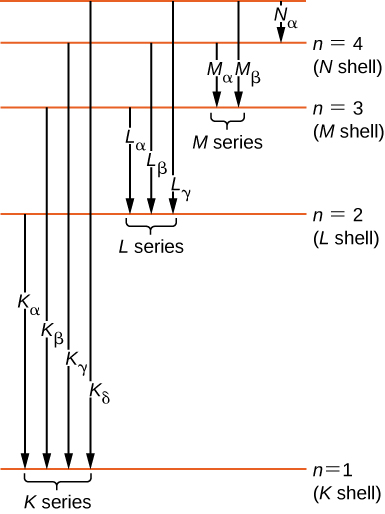
تاريخيًا، تم تصنيف الخطوط الطيفية للأشعة السينية بأحرف (K، L، M، N،...). تتوافق هذه الحروف مع الأصداف الذرية (\(n = 1,2,3,4,...\)). يتم تصنيف الأشعة السينية الناتجة عن الانتقال من أي غلاف أعلى إلى غلاف K (\(n = 1\)) بالأشعة السينية K. تسمى الأشعة السينية التي يتم إنتاجها في مرحلة انتقالية من الغلاف L (\(n = 2\))\(K_{\alpha}\) بالأشعة السينية؛ وتسمى الأشعة السينية المنتجة في مرحلة انتقالية من غلاف M (\(n = 3\)) بالأشعة\(K_{\beta}\) السينية؛ وتسمى الأشعة السينية المنتجة في الانتقال من الغلاف N (\(n = 4\)) \(K_{\gamma}\)الأشعة السينية؛ وهكذا دواليك. يتم تصنيف التحولات من الأصداف الأعلى إلى قذائف L و M بالمثل. يتم تمثيل هذه التحولات من خلال رسم تخطيطي لمستوى الطاقة في الشكل\(\PageIndex{5}\).
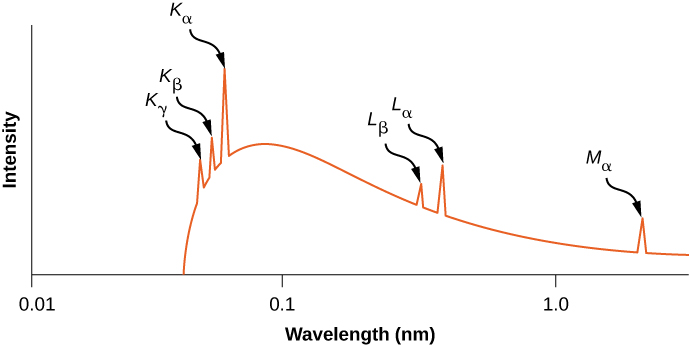
يوضح الشكل توزيع الأطوال الموجية للأشعة السينية الناتجة عن ضرب المعدن بشعاع من الإلكترونات\(\PageIndex{6}\). تظهر انتقالات الأشعة السينية في المعدن المستهدف كقمم أعلى منحنى إشعاع الكبح. تسمى ترددات الفوتون المقابلة للطفرات في توزيع الأشعة السينية بالترددات المميزة، لأنها يمكن استخدامها لتحديد المعدن المستهدف. يتوافق الطول الموجي للقطع الحاد (أقل بقليل من\(K_{\gamma}\) الذروة) مع الإلكترون الذي يفقد كل طاقته لصالح فوتون واحد. يحظر الإشعاع ذي الأطوال الموجية الأقصر من خلال الحفاظ على الطاقة.
تقدير الطاقة المميزة وتردد\(K_{\alpha}\) الأشعة السينية للألمنيوم (\(Z = 13\)).
إستراتيجية
يتم إنتاج\(K_{\alpha}\) الأشعة السينية من خلال انتقال الإلكترون في الغلاف L (\(n=2\)) إلى الغلاف K (\(n = 1\)). الإلكترون الموجود في الغلاف L «يرى» شحنة فعالة\(Z = 13 - 1 = 12\)، لأن إلكترون واحد في الغلاف K يحمي الشحنة النووية. (تذكر أن إلكترونين ليسا في غلاف K لأن حالة الإلكترون الأخرى خالية.) يمكن تقدير تردد الفوتون المنبعث من فرق الطاقة بين قذائف L و K.
الحل
فرق الطاقة بين قذائف L و K في ذرة الهيدروجين هو 10.2 eV. بافتراض أن الإلكترونات الأخرى في الغلاف L أو في الأصداف ذات الطاقة العالية لا تحمي الشحنة النووية، فإن فرق الطاقة بين قذائف L و K في الذرة مع\(Z = 13\)
\[\begin{align*} E_{L \rightarrow K} &\approx (Z - 1)^2 (10.2 \, eV) \\[4pt] &\approx (13 - 1)^2(10.2 \, eV) \\[4pt] &\approx 1.47 \times 10^3 eV. \end{align*} \nonumber \]
بناءً على العلاقة\(f = (\Delta E_{L \rightarrow K})/h\)، يكون تردد الأشعة السينية هو
\[f = \frac{1.47 \times 10^3 eV}{4.14 \times 10^{-15} eV \cdot s} = 3.55 \times 10^{17} Hz. \nonumber \]
الدلالة
الطول الموجي للأشعة السينية النموذجية هو 0.1-10 نانومتر. في هذه الحالة، يكون الطول الموجي هو:
\[\lambda = \frac{c}{f} = \frac{3.0 \times 10^8 m/s}{3.55 \times 10^{17} Hz} = 8.5 \times 10^{-10} = 0.85 \, nm. \nonumber \]
وبالتالي، فإن الانتقال L → K في الألومنيوم ينتج أشعة سينية.
يوفر إنتاج الأشعة السينية اختبارًا مهمًا لميكانيكا الكم. وفقًا لنموذج Bohr، تعتمد طاقة\(K_{\alpha}\) الأشعة السينية على الشحنة النووية أو الرقم الذري Z. إذا كانت Z كبيرة، تكون قوى الكولوم في الذرة كبيرة، وفروق الطاقة (\(\Delta E\)) كبيرة، وبالتالي فإن طاقة الفوتونات المشعة كبيرة. للتوضيح، ضع في اعتبارك إلكترون واحد في ذرة متعددة الإلكترون. عند إهمال التفاعلات بين الإلكترونات، تكون مستويات الطاقة المسموح بها هي
\[E_n = -\frac{Z^2(13.6 \, eV)}{n^2}, \nonumber \]
حيث n = 1، 2،... و Z هو العدد الذري للنواة. ومع ذلك، فإن الإلكترون الموجود في الغلاف L (\(n = 2\)) «يرى» الشحنة\(Z - 1\)، لأن إلكترون واحد في الغلاف K يحمي الشحنة النووية. (تذكر أن هناك إلكترون واحد فقط في غلاف K لأن الإلكترون الآخر «تم طرده».) لذلك، فإن الطاقات التقريبية للإلكترون في قذائف L و K هي
\[E_L \approx - \frac{(Z - 1)^2(13.6 \, eV)}{2^2} \nonumber \]
\[E_K \approx - \frac{(Z - 1)^2(13.6 \, eV)}{1^2}. \nonumber \]
وبالتالي فإن الطاقة التي يحملها الفوتون في الانتقال من الغلاف L إلى غلاف K هي
\[ \begin{align*} \Delta E_{L \rightarrow K} &= (Z - 1)^2 (13.6 \, eV)\left(\frac{1}{1^2} - \frac{1}{2^2} \right) \\[4pt] &= (Z - 1)^2 (10.2 \, eV), \end{align*} \nonumber \]
حيث Z هو الرقم الذري. بشكل عام، تكون طاقة الفوتون بالأشعة السينية للانتقال من الغلاف الخارجي إلى الغلاف K
\[E_{L\rightarrow K} = hf = constant \times (Z - 1)^2, \nonumber \]
أو
\[(Z - 1) = constant \sqrt{f}, \nonumber \]
\(f\)أين تردد الأشعة\(K_{\alpha}\) السينية. هذه المعادلة هي قانون موسلي. بالنسبة للقيم الكبيرة\(Z\)، لدينا ما يقرب من
\[Z \approx constant \sqrt{f}. \nonumber \]
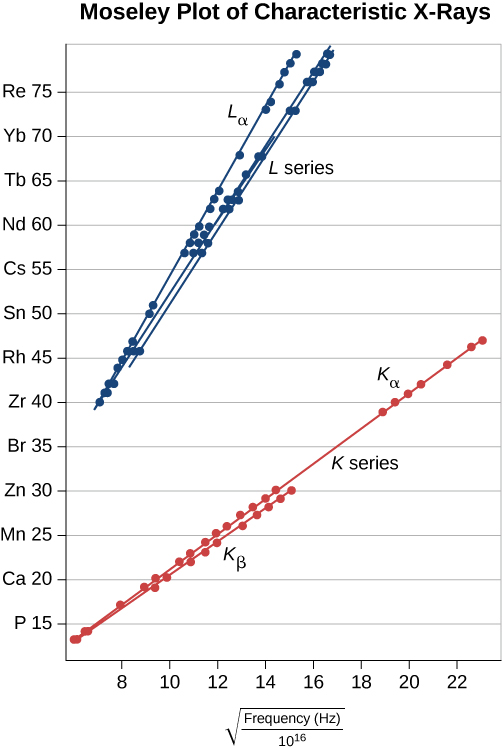
يمكن التحقق من هذا التوقع من خلال قياس\(f\) مجموعة متنوعة من الأهداف المعدنية. يتم دعم هذا النموذج إذا كانت قطعة Z مقابل\(\sqrt{f}\) البيانات (تسمى مخطط Moseley) خطية. تظهر مقارنة تنبؤات النماذج والنتائج التجريبية لكل من سلسلتي K و L في الشكل\(\PageIndex{7}\). تدعم البيانات النموذج الذي يتم فيه إنتاج الأشعة السينية عندما ينخفض إلكترون الغلاف الخارجي في الطاقة لملء الفراغ في الغلاف الداخلي.
يتم إنتاج الأشعة السينية عن طريق قصف هدف معدني بإلكترونات عالية الطاقة. إذا تم استبدال الهدف بآخر بضعفي العدد الذري، فماذا يحدث لتردد الأشعة السينية؟
- إجابة
-
أربعة أضعاف التردد
احسب الطاقة التقريبية\(K_{\alpha}\) للأشعة السينية من أنود التنجستن في أنبوب الأشعة السينية.
إستراتيجية
يحتل إلكترونان غلاف K مملوء. سيؤدي الفراغ الموجود في هذه القشرة إلى ترك إلكترون واحد، وبالتالي فإن الشحنة الفعالة للإلكترون في الغلاف L ستكون Z − 1 بدلاً من Z. بالنسبة للتنجستن، Z = 74، وبالتالي فإن الشحنة الفعالة هي 73. يمكن استخدام هذا الرقم لحساب فرق مستوى الطاقة بين قذائف L و K، وبالتالي الطاقة التي يحملها الفوتون في المرحلة الانتقالية L←K.
الحل
Z الفعال هو 73، لذلك يتم إعطاء طاقة\(K_{\alpha}\) الأشعة السينية بواسطة
\[E_{K_{\alpha}} = \Delta E = E_i - E_f = E_2 - E_1, \nonumber \]
حيث
\[E_1 = - \frac{Z^2}{1^2}E_0 = - \frac{73^2}{1}(13.6 \, eV) = - 72.5 \, keV \nonumber \]
و
\[E_2 = - \frac{Z^2}{2^2}E_0 = - \frac{73^2}{4}(13.6 \, eV) = -18.1 \, keV. \nonumber \]
وهكذا،
\[E_{K_{\alpha}} = - 18.1 \, keV - (- 72.5 \, keV) = 54.4 \, keV. \nonumber \]
الدلالة
تعتبر طاقة الفوتون الكبيرة هذه نموذجية للأشعة السينية. تصبح طاقات الأشعة السينية أكبر تدريجيًا بالنسبة للعناصر الثقيلة لأن طاقتها تزداد تقريبًا\(Z^2\). هناك حاجة إلى جهد تسارع يزيد عن 50000 فولت «لإخراج» إلكترون داخلي من ذرة التنغستن.
تقنية الأشعة السينية
الأشعة السينية لها العديد من التطبيقات، مثل التشخيص الطبي (الشكل\(\PageIndex{8}\))، وفحص الأمتعة في المطارات (الشكل\(\PageIndex{9}\))، وحتى الكشف عن الشقوق في مكونات الطائرات الهامة. تعود صور الأشعة السينية الأكثر شيوعًا إلى الظلال. نظرًا لأن فوتونات الأشعة السينية تتمتع بطاقة عالية، فإنها تخترق المواد غير الشفافة للضوء المرئي. كلما زادت طاقة فوتون الأشعة السينية، زادت المواد التي يخترقها. يرتبط عمق الاختراق بكثافة المادة، وكذلك بطاقة الفوتون. كلما زادت كثافة المادة، قل عدد فوتونات الأشعة السينية التي تمر بها وزاد لون الظل. تعتبر الأشعة السينية فعالة في تحديد كسور العظام والأورام؛ ومع ذلك، يمكن أن يؤدي التعرض المفرط للأشعة السينية إلى تلف الخلايا في الكائنات البيولوجية.
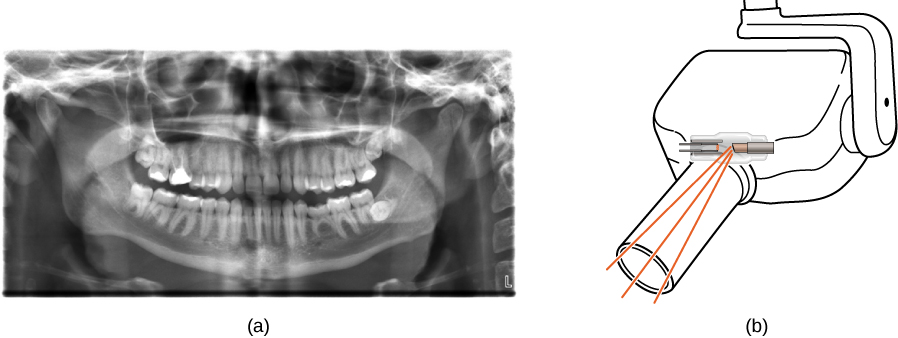

توفر صورة الأشعة السينية القياسية عرضًا ثنائي الأبعاد للكائن. ومع ذلك، في التطبيقات الطبية، لا توفر وجهة النظر هذه في كثير من الأحيان معلومات كافية لاستخلاص استنتاجات ثابتة. على سبيل المثال، في صورة الأشعة السينية ثنائية الأبعاد للجسم، يمكن للعظام إخفاء الأنسجة الرخوة أو الأعضاء بسهولة. يعالج ماسح CAT (التصوير المقطعي المحوري) هذه المشكلة من خلال جمع العديد من صور الأشعة السينية في «شرائح» في جميع أنحاء الجسم. يمكن أن تؤدي المعالجة المعقدة للصور الحاسوبية للامتصاص النسبي للأشعة السينية، في اتجاهات مختلفة، إلى إنتاج صورة أشعة سينية ثلاثية الأبعاد مفصلة للغاية للجسم.
يمكن أيضًا استخدام الأشعة السينية لاستكشاف هياكل الذرات والجزيئات. ضع في اعتبارك حادثة الأشعة السينية على سطح مادة صلبة بلورية. تنعكس بعض فوتونات الأشعة السينية على السطح، بينما ينعكس البعض الآخر عن «مستوى» الذرات الموجودة أسفل السطح مباشرةً. ينتج التداخل بين هذه الفوتونات، لزوايا الإصابة المختلفة، صورة جميلة على الشاشة (الشكل\(\PageIndex{10}\)). يُطلق على تفاعل الأشعة السينية مع مادة صلبة اسم حيود الأشعة السينية. المثال الأكثر شهرة باستخدام حيود الأشعة السينية هو اكتشاف البنية الحلزونية المزدوجة للحمض النووي.



