8.2: ذرة الهيدروجين
- Page ID
- 196745
في نهاية هذا القسم، ستكون قادرًا على:
- وصف ذرة الهيدروجين بدلالة دالة الموجة وكثافة الاحتمالية والطاقة الكلية والزخم الزاوي المداري
- حدد الأهمية الفيزيائية لكل من الأرقام الكمومية (n، l، m) لذرة الهيدروجين
- قم بالتمييز بين نماذج Bohr و Schrödinger للذرة
- استخدم الأرقام الكمومية لحساب المعلومات المهمة حول ذرة الهيدروجين
ذرة الهيدروجين هي أبسط ذرة في الطبيعة، وبالتالي فهي نقطة انطلاق جيدة لدراسة الذرات والبنية الذرية. تتكون ذرة الهيدروجين من إلكترون واحد سالب الشحنة يتحرك حول بروتون موجبة الشحنة (الشكل\(\PageIndex{1}\)). في نموذج Bohr، يتم سحب الإلكترون حول البروتون في مدار دائري تمامًا بواسطة قوة كولوم الجذابة. يبلغ حجم البروتون حوالي 1800 مرة أكبر من الإلكترون، لذلك يتحرك البروتون قليلاً جدًا استجابة لقوة الإلكترون على البروتون. (وهذا مشابه لنظام الأرض والشمس، حيث تتحرك الشمس قليلاً جدًا استجابة للقوة التي تمارسها الأرض عليها.) ويرد شرح لهذا التأثير باستخدام قوانين نيوتن في الفوتونات وموجات المادة.
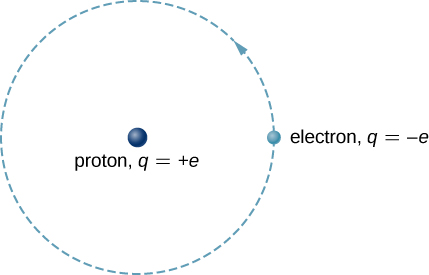
مع افتراض وجود بروتون ثابت، نركز على حركة الإلكترون.
في المجال الكهربائي للبروتون، تكون الطاقة الكامنة للإلكترون
\[U(r) = -k\frac{e^2}{r}, \nonumber \]
أين\(k = 1/4\pi\epsilon_0\)\(r\) هي المسافة بين الإلكترون والبروتون. كما رأينا سابقًا، القوة المؤثرة على جسم ما تساوي سالب التدرج (أو المنحدر) لدالة الطاقة الكامنة. بالنسبة للحالة الخاصة لذرة الهيدروجين، فإن القوة بين الإلكترون والبروتون هي قوة كولوم الجذابة.
لاحظ أن وظيفة الطاقة المحتملة\(U(r)\) لا تختلف في الوقت. ونتيجة لذلك، تنخفض معادلة شرودنغر لذرة الهيدروجين إلى معادلتين أبسط: واحدة تعتمد فقط على الفضاء (x، y، z) والأخرى تعتمد فقط على الوقت (t). (تمت مناقشة فصل دالة الموجة إلى أجزاء تعتمد على الفضاء والوقت لوظائف الطاقة المحتملة المستقلة عن الوقت في ميكانيكا الكم.) نحن مهتمون أكثر بالمعادلة المعتمدة على الفضاء:
\[\frac{-\hbar}{2m_e}\left(\frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2}\right) - k\frac{e^2}{r}\psi = E\psi, \nonumber \]
أين\(\psi = psi (x,y,z)\) هي وظيفة الموجة ثلاثية الأبعاد للإلكترون، والميم هي كتلة الإلكترون،\(E\) وهي الطاقة الكلية للإلكترون. تذكر أن دالة\(\Psi (x,y,z,t)\) الموجة الكلية هي نتاج وظيفة الموجة المعتمدة على الفضاء\(\psi = \psi(x,y,z)\) ووظيفة الموجة المعتمدة على الوقت\(\varphi = \varphi(t)\).
بالإضافة إلى كونها مستقلة عن الوقت،\(U(r)\) فهي أيضًا متماثلة كرويًا. يشير هذا إلى أننا قد نحل معادلة شرودنغر بسهولة أكبر إذا عبرنا عنها من حيث الإحداثيات الكروية (\(r, \theta, \phi\)) بدلاً من الإحداثيات المستطيلة (\(x,y,z\)). يظهر نظام الإحداثيات الكروية في الشكل\(\PageIndex{2}\). في الإحداثيات الكروية،\(r\) يكون المتغير هو الإحداثيات الشعاعية،\(\theta\) وهي الزاوية القطبية (بالنسبة إلى المحور z الرأسي)،\(\phi\) وهي الزاوية السمتي (بالنسبة إلى المحور x). العلاقة بين الإحداثيات الكروية والمستطيلة هي\(x = r \, \sin \, \theta \, \cos \, \phi\)،\(y = r \, \sin \theta \, \sin \, \phi\)،\(z = r \, \cos \, \theta\).
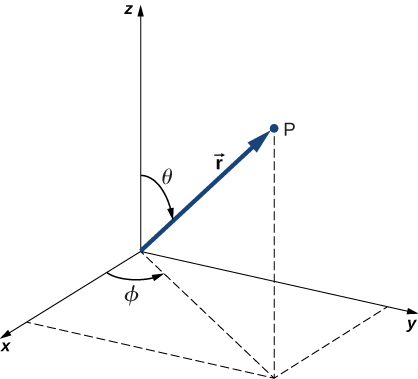
العامل\(r \, \sin \, \theta\) هو حجم المتجه الذي يتكون من إسقاط المتجه القطبي على المستوى xy. أيضًا، يتم الحصول على إحداثيات x و y عن طريق إسقاط هذا المتجه على المحاور x - و y، على التوالي. يعطي التحول العكسي
\[\begin{align*} r &= \sqrt{x^2 + y^2 + z^2} \\[4pt] \theta &= \cos^{-1} \left(\frac{z}{r}\right), \\[4pt] \phi &= \cos^{-1} \left( \frac{x}{\sqrt{x^2 + y^2}}\right) \end{align*} \nonumber \]
تمت مناقشة معادلة الموجة لشرودنجر لذرة الهيدروجين في الإحداثيات الكروية في دورات أكثر تقدمًا في الفيزياء الحديثة، لذلك لا نعتبرها بالتفصيل هنا. ومع ذلك، وبسبب التماثل الكروي لـ\(U(r)\)، تنخفض هذه المعادلة إلى ثلاث معادلات أبسط: واحدة لكل من الإحداثيات الثلاثة (\(r\)،\(θ\)، و\(ϕ\)). تتم كتابة حلول وظيفة الموجة المستقلة عن الوقت كمنتج لثلاث وظائف:
\[\psi (r, \theta, \phi) = R(r) \Theta(\theta) \Phi (\phi), \nonumber \]
\(R\)أين تعتمد الوظيفة الشعاعية على الإحداثيات الشعاعية\(r\) فقط؛\(Θ\) هل تعتمد الوظيفة القطبية على الإحداثيات القطبية\(θ\) فقط؛\(Φ\) وهي وظيفة phi\(ϕ\) فقط. \(ψ(r, θ, ϕ)\)يتم تصنيف الحلول الصالحة لمعادلة شرودنغر بالأرقام الكمومية\(n\)\(l\) و و\(m\).
- \(n\): رقم الكم الرئيسي
- \(l\): العدد الكمي للزخم الزاوي
- \(m\): الرقم الكمي للإسقاط الزاوي للزخم
(سيتم شرح أسباب هذه الأسماء في القسم التالي.) \(R\)تعتمد الوظيفة الشعاعية فقط على\(n\) و\(l\)؛\(\Theta\) تعتمد الوظيفة القطبية فقط على\(l\) و\(m\)؛\(\Phi\) وتعتمد وظيفة phi فقط على\(m\). يُشار إلى اعتماد كل دالة على الأرقام الكمومية باستخدام الرموز الفرعية:
\[\psi_{nlm}(r, \theta, \phi) = R_{nl}(r)\Theta_{lm}(\theta)\Phi_m(\phi). \nonumber \]
ليست كل مجموعات الأرقام الكمومية (\(n\)\(l\)،،\(m\)) ممكنة. على سبيل المثال، لا\(l\) يمكن أبدًا أن يكون الرقم الكمي الزاوي المداري أكبر أو مساويًا للرقم الكمي الرئيسي\(n(l < n)\). على وجه التحديد، لدينا
- \(n = 1,2,3,...\)
- \(l = 0,1,2,...,(n-1)\)
- \(m = -l, (-l+1), . . ., 0, . . ., (+l - 1), +l\)
لاحظ أنه بالنسبة للحالة الأرضية، و\(n = 1\)\(l = 0\)، و\(m = 0\). بعبارة أخرى، هناك حالة كمية واحدة فقط مع دالة الموجة لـ\(n = 1\)، وهي كذلك\(\psi_{100}\). ومع ذلك\(n = 2\)، لدينا
\[l = 0, \, m = 0 \nonumber \]
و
\[l = 1, \, m = -1, 0, 1. \nonumber \]
لذلك، فإن الحالات المسموح بها\(n = 2\) للدولة هي\(\psi_{200}\)\(\psi_{21-1}\) و\(\psi_{210}\) و و\(\psi_{211}\). يتم إعطاء أمثلة لوظائف الموجة لذرة الهيدروجين في الجدول\(\PageIndex{1}\). لاحظ أن بعض هذه التعبيرات تحتوي على الحرف\(i\) الذي يمثل\(\sqrt{-1}\). عند حساب الاحتمالات، لا تظهر هذه الأرقام المعقدة في الإجابة النهائية.
| \(n = 1, \, l = 0, \, m_l = 0\) | \(\displaystyle \psi_{100} = \frac{1}{\sqrt{\pi}} \frac{1}{a_0^{3/2}}e^{-r/a_0}\) |
| \(n = 2, \, l = 0, \, m_l = 0\) | \(\displaystyle\psi_{200} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}(2 - \frac{r}{a_0})e^{-r/2a_0}\) |
| \(n = 2, \, l = 1, \, m_l = -1\) | \(\displaystyle\psi_{21-1} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{-i\phi}\) |
| \(n = 2, \, l = 1, \, m_l = 0\) | \( \displaystyle \psi_{210} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\cos \, \theta\) |
| \(n = 2, \, l = 1, \, m_l = 1\) | \( \displaystyle\psi_{211} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{i\phi}\) |
الأهمية الفيزيائية للأعداد الكمومية
يرتبط كل رقم من الأرقام الكمومية الثلاثة لذرة الهيدروجين (\(n\)\(l\)،،\(m\)) بكمية فيزيائية مختلفة.
رقم الكم الرئيسي
\(n\)يرتبط الرقم الكمي الرئيسي بالطاقة الكلية للإلكترون،\(E_n\). وفقًا لمعادلة شرودنغر:
\[E_n = - \left(\frac{m_ek^2e^4}{2\hbar^2}\right)\left(\frac{1}{n^2}\right) = - E_0 \left(\frac{1}{n^2}\right), \label{8.3} \]
أين\(E_0 = -13.6 \, eV\). لاحظ أن هذا التعبير مطابق لتعبير نموذج Bohr. كما هو الحال في نموذج Bohr، لا يشع الإلكترون في حالة معينة من الطاقة.
بالنسبة لذرة الهيدروجين، ما عدد الحالات الكمومية الممكنة التي تتوافق مع الرقم الأساسي\(n = 3\)؟ ما هي طاقات هذه الدول؟
إستراتيجية
بالنسبة لذرة الهيدروجين لطاقة معينة، يعتمد عدد الحالات المسموح بها على زخمها الزاوي المداري. يمكننا حساب هذه الحالات لكل قيمة من العدد الكمي الأساسي،\(n = 1,2,3\). ومع ذلك، تعتمد الطاقة الإجمالية على الرقم الكمي الرئيسي فقط، مما يعني أنه يمكننا استخدام المعادلة\ ref {8.3} وعدد الحالات المحسوبة.
الحل
إذا كانت\(n = 3\) القيم المسموح بها\(l\) هي 0 و1 و2. إذا\(l = 0\)،\(m = 0\) (ولاية واحدة). إذا\(l = 1\)،\(m = -1, 0, 1\) (3 ولايات)؛ وإذا\(l = 2\)،\(m = -2, -1, 0, 1, 2\) (5 ولايات). في المجموع، هناك 1 + 3 + 5 = 9 حالات مسموح بها. نظرًا لأن إجمالي الطاقة يعتمد فقط على العدد الكمي الرئيسي\(n = 3\)، فإن طاقة كل من هذه الحالات هي
\[E_{n3} = -E_0 \left(\frac{1}{n^2}\right) = \frac{-13.6 \, eV}{9} = - 1.51 \, eV. \nonumber \]
الأهمية
يمكن للإلكترون في ذرة الهيدروجين أن يشغل العديد من حالات الزخم الزاوي المختلفة بنفس الطاقة. مع زيادة الزخم الزاوي المداري، يزداد عدد الحالات المسموح بها بنفس الطاقة.
العدد الكمي المداري للزخم الزاوي
\(l\)يرتبط الرقم الكمي المداري للزخم الزاوي بالزخم الزاوي المداري للإلكترون في ذرة الهيدروجين. تخبرنا نظرية الكم أنه عندما تكون ذرة الهيدروجين في الحالة\(\psi_{nlm}\)، يكون حجم زخمها الزاوي المداري
\[L = \sqrt{l(l + 1)}\hbar, \nonumber \]
أين\(l = 0, 1, 2, . . . , (n - 1)\).
تختلف هذه النتيجة قليلاً عن تلك الموجودة في نظرية بوهر، التي تحدد كمية الزخم الزاوي وفقًا للقاعدة\(L = n\)، حيث\(n = 1,2,3, ...\)
يتم تمييز الحالات الكمومية ذات القيم المختلفة للزخم الزاوي المداري باستخدام الترميز الطيفي (الجدول\(\PageIndex{2}\)). نتجت التسميات s و p و d و f عن محاولات تاريخية مبكرة لتصنيف الخطوط الطيفية الذرية. (تشير الحروف إلى الحروف الحادة والأساسية والمنتشرة والأساسية، على التوالي.) بعد f، تستمر الحروف أبجديًا.
يتم تحديد الحالة الأرضية للهيدروجين كحالة 1 ثانية، حيث تشير «1" إلى مستوى الطاقة (\(n = 1\)) وتشير «s» إلى حالة الزخم الزاوي المداري (\(l = 0\)). متى\(n = 2\)،\(l\) يمكن أن يكون إما 0 أو 1. يتم\(n = 2\) تسمية\(l = 0\) الدولة بـ «2 ثانية». تم\(n = 2\) تسمية\(l = 1\) الدولة بـ «2 ص». عندما\(n = 3\)،\(l\) يمكن أن تكون 0 أو 1 أو 2، والحالات هي 3 ثوان، 3 ص، و 3 د، على التوالي. يتم إعطاء الترميز للحالات الكمومية الأخرى في الجدول\(\PageIndex{3}\).
| رقم الكم المداري\(l\) | الزخم الزاوي | حالة | الاسم الطيفي |
|---|---|---|---|
| \ (l\) ">0 | 0 | ثانية | شارب |
| \ (l\) ">1 | \(\sqrt{2}h\) | ص | المالك |
| \ (l\) ">2 | \(\sqrt{6}h\) | د | منتشر |
| \ (l\) ">3 | \(\sqrt{12}h\) | و | أساسي |
| \ (l\) ">4 | \(\sqrt{20}h\) | ز | |
| \ (l\) ">5 | \(\sqrt{30}h\) | ح |
العدد الكمي للإسقاط الزاوي للزخم
\(m\)يرتبط الرقم الكمي لإسقاط الزخم الزاوي بزاوية السمت\(\phi\) (انظر الشكل\(\PageIndex{2}\)) ويرتبط بالمكون z للزخم الزاوي المداري للإلكترون في ذرة الهيدروجين. يتم تقديم هذا المكون من خلال
\[L_z = m\hbar, \nonumber \]
أين\(m = -l, -l + 1, ..., 0, ..., +l - 1, l\).
يرتبط مكون z للزخم الزاوي بحجم الزخم الزاوي بمقدار الزخم الزاوي
\[L_z = L \, \cos \theta, \nonumber \]
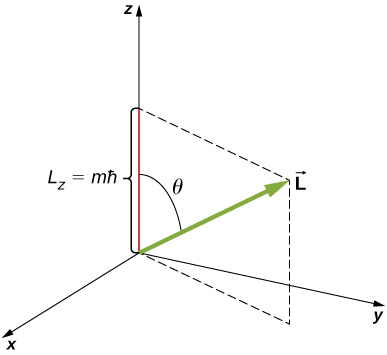
\(\theta\)أين الزاوية بين متجه الزخم الزاوي والمحور z. لاحظ أن اتجاه المحور z يتم تحديده من خلال التجربة - أي على أي اتجاه، يقرر المجرب قياس الزخم الزاوي. على سبيل المثال، قد يتوافق اتجاه z مع اتجاه المجال المغناطيسي الخارجي. العلاقة بين\(L_z\) و\(L\) موضحة في الشكل\(\PageIndex{3}\).
| \(l = 0\) | \(l = 1\) | \(l = 2\) | \(l = 3\) | \(l = 4\) | \(l = 5\) | |
| \(n = 1\) | 1 ثانية | |||||
| \(n = 2\) | 2 ثانية | 2 ص | ||||
| \(n = 3\) | 3 ثانية | 3 ص | 3 د | |||
| \(n = 4\) | 4 ثانية | 4 ص | 4 د | 4 غرام | ||
| \(n = 5\) | 5 ثانية | 5 ص | 5 د | 5 غرام | 5 جرام | |
| \(n = 6\) | 6 ثانية | 6 ص | 6 د | 6 غرام | 6 جرام | 6 ساعة |
إن التحديد الكمي\(L_z\) يعادل التحديد الكمي لـ\(\theta\). \(L\)\(m\)وبالتعويض\(\sqrt{l(l + 1)}\hbar\) عن هذه المعادلة وإدراجها، نجد\(L_z\)
\[m\hbar = \sqrt{l(l + 1)}\hbar \, \cos \, \theta. \nonumber \]
وبالتالي،\(\theta\) يتم تحديد الزاوية بالقيم الخاصة
\[\theta = \cos^{-1}\left(\frac{m}{\sqrt{l(l + 1)}}\right). \nonumber \]
لاحظ أنه تم تحديد كل من الزاوية القطبية (\(θ\)) وإسقاط متجه الزخم الزاوي على محور z -عشوائي (\(L_z\)).
يظهر تحديد مقدار الزاوية القطبية\(l = 3\) للحالة في الشكل\(\PageIndex{4}\). يقع متجه الزخم الزاوي المداري في مكان ما على سطح مخروط بزاوية فتح\(\theta\) بالنسبة إلى المحور z (ما لم تكن\(m = 0\) نقاط المتجه في هذه الحالة\(θ = 90^o\) متعامدة مع المحور z).
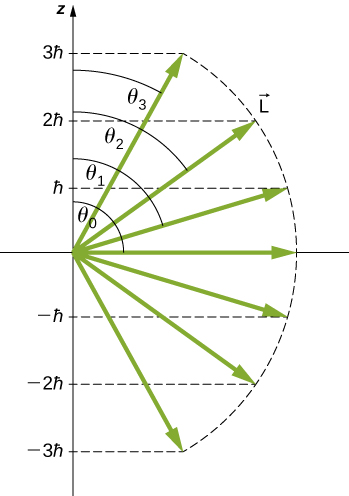
تكشف دراسة مفصلة للزخم الزاوي أننا لا نستطيع معرفة المكونات الثلاثة في وقت واحد. في القسم السابق، يحتوي المكون z في الزخم الزاوي المداري على قيم محددة تعتمد على الرقم الكمي\(m\). هذا يعني أننا لا نستطيع معرفة كل من مكونات x- و y للزخم الزاوي\(L_y\)،\(L_x\) وبشكل مؤكد. ونتيجة لذلك، فإن الاتجاه الدقيق لمتجه الزخم الزاوي المداري غير معروف.
احسب الزوايا التي\(\vec{L}\) يمكن لمتجه الزخم الزاوي تكوينها باستخدام المحور z\(l = 1\)، كما هو موضح في الشكل\(\PageIndex{5}\).
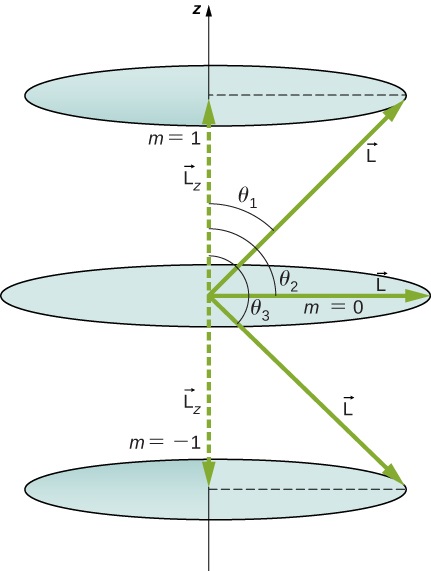
إستراتيجية
تشكل المتجهات\(\vec{L}\) و\(\vec{L_z}\) (في الاتجاه z) مثلثًا قائمًا، حيث\(\vec{L}\) يوجد الوتر\(\vec{L_z}\) وهو الجانب المجاور. النسبة\(L_z\) إلى |\(\vec{L}\) | هي جيب التمام لزاوية الاهتمام. المقادير\(L = |\vec{L}|\)\(L_z\) ويتم إعطاؤها بواسطة
\[L = \sqrt{l(l + 1)} \hbar \nonumber \]
و
\[L_z = m\hbar. \nonumber \]
الحل
يتم إعطاؤنا\(l = 1\)، لذلك\(m\) يمكن أن نكون +1 أو 0 أو +1. وبالتالي،\(L\) لديه القيمة المعطاة من
\[L = \sqrt{l(l + 1)}\hbar = \sqrt{2}\hbar. \nonumber \]
\(L_z\)يمكن أن تحتوي الكمية على ثلاث قيم، معطاة بـ\(L_z = m_l\hbar\).
\[L_z = \begin{cases} \hbar, & \text{if } m_l=+1 \\ 0, & \text{if } m_l=0 \\ \hbar, & \text{if } m_l=-1 \end{cases} \nonumber \]
كما ترون في الشكل\(\PageIndex{5}\)\(\cosθ=Lz/L\)\(m=+1\)، لذلك لدينا
\[\cos \, \theta_1 = \frac{L_z}{L} = \frac{\hbar}{\sqrt{2}\hbar} = \frac{1}{\sqrt{2}} = 0.707 \nonumber \]
وهكذا،
\[\theta_1 = \cos^{-1}0.707 = 45.0°. \nonumber \]
وبالمثل\(m = 0\)، نجد\(\cos \, \theta_2 = 0\)؛ هذا يعطي
\[\theta_2 = \cos^{-1}0 = 90.0°. \nonumber \]
ثم من أجل\(m_l = -1\):
\[\cos \, \theta_3 = \frac{L_Z}{L} = \frac{-\hbar}{\sqrt{2}\hbar} = -\frac{1}{\sqrt{2}} = -0.707, \nonumber \]
بحيث
\[\theta_3 = \cos^{-1}(-0.707) = 135.0°. \nonumber \]
الأهمية
تتوافق الزوايا مع الشكل. يتم تحديد الزاوية بالنسبة للمحور z فقط. \(L\)يمكن أن يشير في أي اتجاه طالما أنه يصنع الزاوية المناسبة مع المحور z. وهكذا، تقع متجهات الزخم الزاوي على الأقماع، كما هو موضح. لمعرفة كيفية ثبات مبدأ المراسلات هنا، ضع في اعتبارك أن أصغر زاوية (\(\theta_1\)في المثال) هي القيمة القصوى لـ\(m_l\)، أي\(m_l = l\). لتلك الزاوية الأصغر،
\[\cos \, \theta = \dfrac{L_z}{L} = \dfrac{l}{\sqrt{l(l + 1)}}, \nonumber \]
الذي يقترب من 1 عندما\(l\) يصبح كبيرًا جدًا. إذا\(cos \, \theta = 1\)، إذن\(\theta = 0º\). علاوة على ذلك\(l\)، بالنسبة للحجم الكبير، هناك العديد من القيم\(m_l\)، بحيث تصبح جميع الزوايا ممكنة\(l\) كلما أصبحت كبيرة جدًا.
هل يمكن أن يكون الحجم\(L_z\) مساويًا لـ\(L\)؟
- إجابة
-
لا. الرقم الكمي\(m = -l, -l + l, ..., 0, ..., l -1, l\). وبالتالي، يكون حجمه\(L_z\) دائمًا أقل من\(L\) السبب\(<\sqrt{l(l + 1)}\)
استخدام دالة الموجة لعمل تنبؤات
كما رأينا سابقًا، يمكننا استخدام ميكانيكا الكم لعمل تنبؤات حول الأحداث المادية باستخدام بيانات الاحتمالات. لذلك من المناسب ذكر أن «الإلكترون موجود داخل هذا المجلد مع وجود هذا الاحتمال في هذا الوقت»، ولكن ليس «يوجد الإلكترون في الموضع (x، y، z) في هذا الوقت.» لتحديد احتمال العثور على إلكترون في ذرة الهيدروجين في منطقة معينة من الفضاء، من الضروري دمج الكثافة الاحتمالية\ (|_ {nlm} |^2) _ فوق تلك المنطقة:
\[\text{Probability} = \int_{volume} |\psi_{nlm}|^2 dV, \nonumber \]
أين\(dV\) يوجد عنصر حجم متناهي الصغر. إذا تم حساب هذا التكامل لكل المساحة، تكون النتيجة 1، لأن احتمال وجود الجسيم في مكان ما هو 100٪ (حالة التطبيع). في دورة أكثر تقدمًا في الفيزياء الحديثة\(|\psi_{nlm}|^2 = \psi_{nlm}^* \psi_{nlm}\)، ستجد\(\psi_{nlm}^*\) أين المترافق المعقد. هذا يزيل التكرارات\(i = \sqrt{-1}\) في الحساب أعلاه.
ضع في اعتبارك الإلكترون في حالة الزخم الزاوي الصفري (\(l = 0\)). في هذه الحالة، تعتمد وظيفة موجة الإلكترون فقط على الإحداثيات الشعاعية\(r\). (راجع الولايات\(\psi_{100}\)\(\psi_{200}\) وفي الجدول\(\PageIndex{1}\).) يتوافق عنصر الحجم المتناهي الصغر مع غلاف كروي نصف قطره\(r\) وسمك متناهي الصغر\(dr\)، مكتوب كـ
\[dV = 4\pi r^2dr. \nonumber \]
احتمال العثور على الإلكترون في المنطقة\(r\) إلى\(r + dr\) («عند r تقريبًا») هو
\[P(r)dr = |\psi_{n00}|^2 4\pi r^2 dr. \nonumber \]
هنا\(P(r)\) تسمى دالة الكثافة الاحتمالية الشعاعية (احتمال لكل وحدة طول). بالنسبة لإلكترون في الحالة الأرضية للهيدروجين، فإن احتمال العثور على إلكترون في المنطقة\(r\)\(r + dr\) هو
\[|\psi_{n00}|^2 4\pi r^2 dr = (4/a_)^3)r^2 exp(-2r/a_0)dr, \nonumber \]
أين\(a_0 = 0.5\) أنجسترومز. تم رسم دالة\(P(r)\) الكثافة الاحتمالية الشعاعية في الشكل\(\PageIndex{6}\). تعطي المساحة الموجودة أسفل المنحنى بين أي موقعين شعاعيين، على سبيل المثال\(r_1\) و\(r_2\)، احتمال العثور على الإلكترون في هذا النطاق الشعاعي. للعثور على الموضع الشعاعي الأكثر احتمالاً، قمنا بتعيين المشتق الأول من هذه الدالة إلى الصفر (\(dP/dr = 0\)) وحل المشكلة\(r\). لا يساوي الموضع الشعاعي الأكثر احتمالاً متوسط أو قيمة التوقع للموضع الشعاعي لأنه\(|\psi_{n00}|^2\) غير متماثل حول قيمة الذروة.
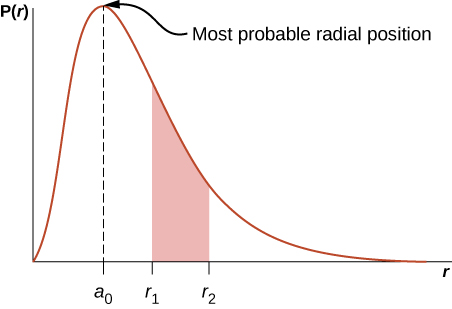
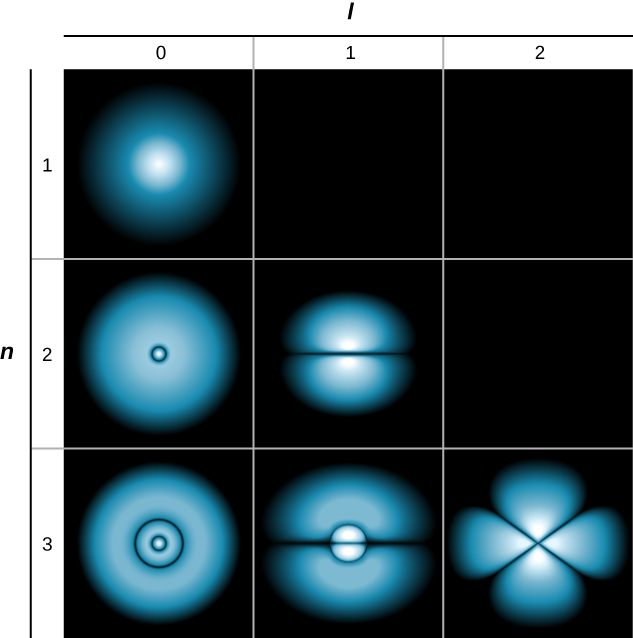
إذا كان للإلكترون زخم زاوي مداري (\(l \neq 0\))، فإن وظائف الموجة التي تمثل الإلكترون تعتمد على الزوايا\(\theta\) و\(\phi\)؛ أي\(\psi_{nlm} = \psi_{nlm}(r, \theta, \phi)\). المدارات الذرية لثلاث ولايات مع\(n = 2\)\(l = 1\) وتظهر في الشكل\(\PageIndex{7}\). المدار الذري هو منطقة في الفضاء تضم نسبة معينة (عادة 90٪) من احتمال الإلكترون. (يشار أحيانًا إلى المدارات الذرية باسم «غيوم» الاحتمالات.) لاحظ أن هذه التوزيعات واضحة في اتجاهات معينة. هذه الاتجاهية مهمة للكيميائيين عندما يحللون كيفية ارتباط الذرات معًا لتكوين الجزيئات.
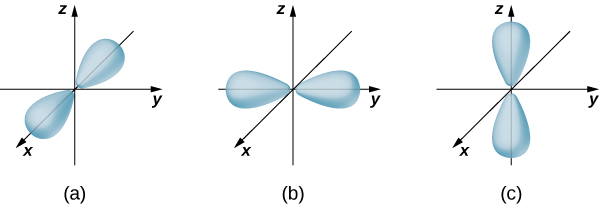
يوجد تمثيل مختلف قليلاً لدالة الموجة في الشكل\(\PageIndex{8}\). في هذه الحالة، تشير المناطق الفاتحة والمظلمة إلى مواقع ذات احتمالية عالية ومنخفضة نسبيًا، على التوالي. على عكس نموذج Bohr لذرة الهيدروجين، لا يتحرك الإلكترون حول نواة البروتون في مسار محدد جيدًا. في الواقع، فإن مبدأ عدم اليقين يجعل من المستحيل معرفة كيفية انتقال الإلكترون من مكان إلى آخر.