Skip to main content
Global

3.2: تدخل يونغ ذو الشق المزدوج

  1. Last updated
  2. Save as PDF
  • Page ID
    196808

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • شرح ظاهرة التداخل
    • تعريف التداخل البناء والمدمر للشق المزدوج

    اعتقد الفيزيائي الهولندي كريستيان هويغنز (1629-1695) أن الضوء عبارة عن موجة، لكن إسحاق نيوتن لم يفعل ذلك. اعتقد نيوتن أن هناك تفسيرات أخرى للون وتأثيرات التداخل والانحراف التي كانت ملحوظة في ذلك الوقت. نظرًا لسمعة نيوتن الهائلة، سادت وجهة نظره بشكل عام؛ لم تعتبر حقيقة نجاح مبدأ Huygens دليلًا مباشرًا يثبت أن الضوء عبارة عن موجة. جاء قبول الطابع الموجي للضوء بعد سنوات عديدة في عام 1801، عندما أظهر الفيزيائي والطبيب الإنجليزي توماس يونغ (1773—1829) تداخلًا بصريًا في تجربته الكلاسيكية ذات الشق المزدوج.

    إذا لم يكن هناك مصدر واحد بل مصدران للموجات، فيمكن جعل الموجات تتداخل، كما هو الحال في الأمواج على الماء (الشكل\(\PageIndex{1}\)). إذا كان الضوء عبارة عن موجة كهرومغناطيسية، فيجب أن يُظهر تأثيرات التداخل في ظل الظروف المناسبة. في تجربة يونغ، تم تمرير ضوء الشمس من خلال ثقب على اللوح. سقط الشعاع الناشئ على فتحتين على لوحة ثانية. ثم سقط الضوء المنبعث من الفتحتين على شاشة حيث لوحظ نمط من البقع الساطعة والمظلمة. لا يمكن تفسير هذا النمط، المسمى بالهامش، إلا من خلال التداخل، وهو ظاهرة موجية.

    تظهر صورة لنمط التداخل. تنبثق الموجات المرئية كدوائر بيضاء على السطح الأزرق من مركزين وتتقاطع عند العديد من النقاط.
    الشكل\(\PageIndex{1}\): صورة لنمط التداخل الناتج عن موجات المياه الدائرية في خزان تموج. يتم اهتزاز غطاسين رقيقين لأعلى ولأسفل على سطح الماء. يتم إنتاج موجات المياه الدائرية وتنبعث من كل مكبس.

    يمكننا تحليل تداخل الشق المزدوج بمساعدة الشكل الذي يصور جهازًا مشابهًا لجهاز يونج\(\PageIndex{2}\)، حيث يسقط الضوء المنبعث من مصدر أحادي اللون على الشق\(S_0\). يسقط الضوء المنبعث\(S_0\) من\(S_1\) شقين\(S_2\) آخرين على مسافة متساوية من\(S_0\). يتم بعد ذلك إنتاج نمط من هامش التداخل على الشاشة بواسطة الضوء المنبعث من\(S_1\) و\(S_2\). يُفترض أن تكون جميع الشقوق ضيقة جدًا بحيث يمكن اعتبارها مصادر نقطية ثانوية لموجات Huygens (طبيعة الضوء). تقع الشقوق\(S_1\) على مسافة d (\(d≤1\,mm\))، والمسافة بين الشاشة والشقوق هي D (≈ 1m)، وهي أكبر بكثير من d.\(S_2\)

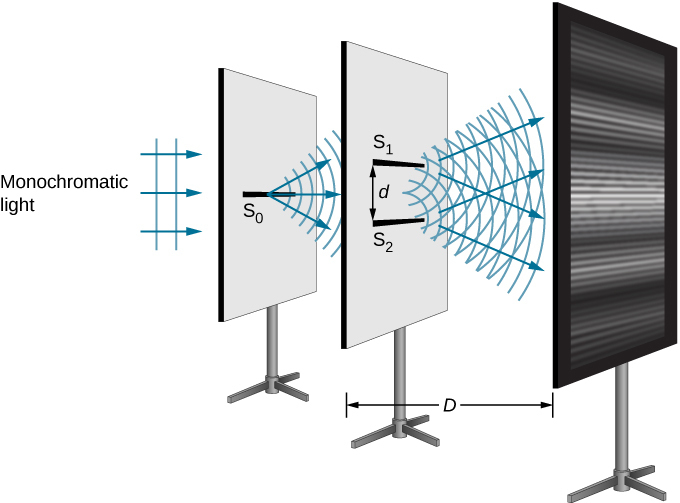
    الصورة عبارة عن رسم تخطيطي لتجربة الشق المزدوج. ينتقل الضوء أحادي اللون أولاً عبر الشق الضيق S0. ثم ينتقل الضوء عبر الفتحتين S1 وS2 الموضعين أحدهما فوق الآخر ويفصل بينهما المسافة d. وأخيرًا، يصل الضوء إلى الشاشة حيث يتشكل نمط التداخل. المسافة بين الشاشة ذات الشق المزدوج والشاشة النهائية هي D.
    الشكل\(\PageIndex{2}\): تجربة التداخل ثنائي الشق باستخدام ضوء أحادي اللون وشقوق ضيقة. يتم ملاحظة الهوامش الناتجة عن تداخل موجات Huygens من الشقوق\(S_1\)\(S_2\) ويتم ملاحظتها على الشاشة.

    نظرًا لأنه\(S_0\) يُفترض أنه مصدر نقطي للضوء أحادي اللون، فإن موجات Huygens الثانوية تغادر\(S_1\) وتحافظ\(S_2\) دائمًا على فرق الطور الثابت (صفر في هذه الحالة لأنها\(S_1\)\(S_2\) متساوية البعد عن\(S_0\)) ولها نفس الشيء التردد. \(S_1\)ثم\(S_2\) يُقال إن المصادر متماسكة. نعني بالموجات المتماسكة أن الموجات في طور أو لها علاقة طورية محددة. يعني مصطلح «غير مترابط» أن الموجات لها علاقات طورية عشوائية، وهو ما سيكون عليه الحال إذا\(S_1\)\(S_2\) تمت إضاءتها بواسطة مصدري ضوء مستقلين، بدلاً من مصدر واحد\(S_0\). إن مصدري الضوء المستقلين (اللذين قد يكونان منطقتين منفصلتين داخل نفس المصباح أو الشمس) لن يصدرا ضوءهما بشكل عام في انسجام تام، أي ليس متماسكًا. أيضًا، نظرًا\(S_1\)\(S_2\) لوجود نفس المسافة\(S_0\) بينهما، فإن سعة موجتي Huygens متساوية.

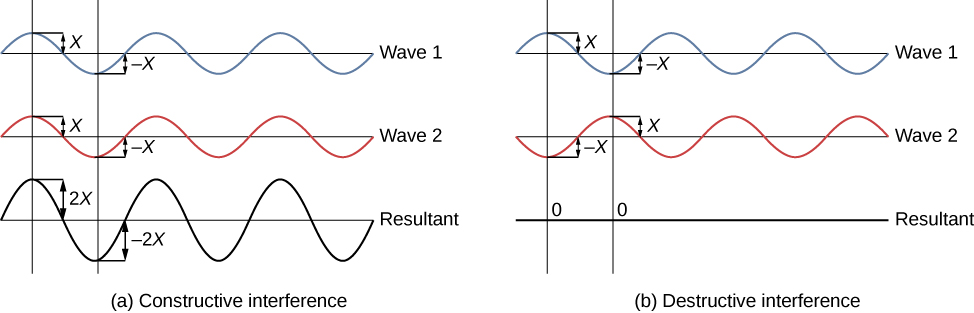
    يستخدم الشباب ضوء الشمس، حيث يشكل كل طول موجة نمطه الخاص، مما يجعل رؤية التأثير أكثر صعوبة. في المناقشة التالية، نوضح تجربة الشق المزدوج باستخدام ضوء أحادي اللون (مفرد) لتوضيح التأثير. \(\PageIndex{3}\)يوضح الشكل التداخل البنائي والمدمر النقي لموجتين لهما نفس الطول الموجي والسعة.

    الصورة اليسرى هي رسم تخطيطي للتداخل البناء. توجد موجتان متطابقتان في الطور مما يؤدي إلى موجة ذات سعة مضاعفة. الصورة الصحيحة هي رسم تخطيطي للتداخل المدمر. يتم إخراج موجتين متطابقتين - تم تحويلهما بمقدار نصف طول موجة - مما يؤدي إلى موجة بسعة صفرية.
    الشكل\(\PageIndex{3}\): تضيف سعات الموجات. (أ) يتم الحصول على التداخل البنائي النقي عندما تكون الموجات المتطابقة في الطور. (ب) يحدث التداخل التدميري النقي عندما تكون الموجات المتطابقة خارج الطور تمامًا، أو تتغير بمقدار نصف طول موجة.

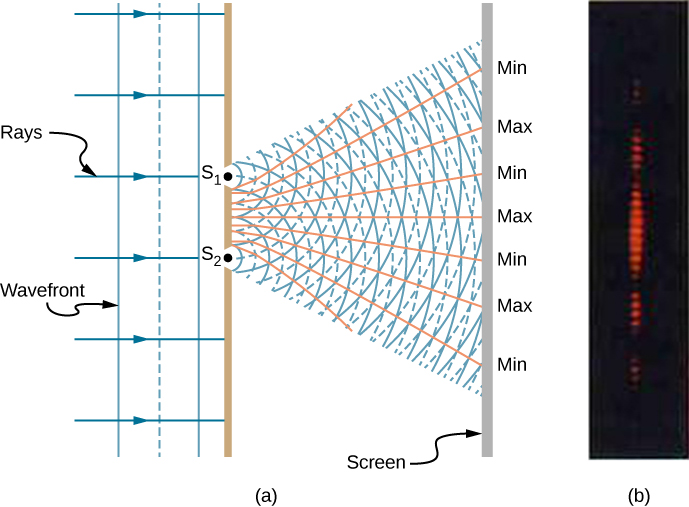
    عندما يمر الضوء عبر الشقوق الضيقة، تعمل الشقوق كمصادر للموجات المتماسكة وينتشر الضوء على شكل موجات نصف دائرية، كما هو موضح في الشكل\(\PageIndex{1a}\). يحدث التداخل البنائي النقي عندما تكون الموجات من القمة إلى القمة أو من الحوض إلى الحوض الصغير. يحدث التداخل المدمر النقي حيث يتم نقلها من القمة إلى الحوض الصغير. يجب أن يسقط الضوء على الشاشة وينتشر في أعيننا حتى نرى النمط. يظهر نمط مماثل لموجات الماء في الشكل\(\PageIndex{1}\). لاحظ أن مناطق التداخل البناء والمدمر تنتقل من الشقوق بزوايا محددة جيدًا إلى الشعاع الأصلي. تعتمد هذه الزوايا على الطول الموجي والمسافة بين الشقوق، كما سنرى أدناه.

    الصورة اليسرى عبارة عن رسم تخطيطي لتجربة الشق المزدوج. يدخل الضوء أحادي اللون الشقين S1 و S2. ينتشر الضوء بعد الانتقال عبر الشقوق مع تداخل الأمواج بشكل بناء ومدمر. الصورة اليمنى هي صورة للنمط الهامشي الذي يُظهر النقاط المضيئة المحاذية كخط.
    الشكل\(\PageIndex{4}\): تنتج الشقوق المزدوجة مصدرين متماسكين للموجات التي تتداخل. (أ) ينتشر الضوء (ينحرف) عن كل شق، لأن الشقوق ضيقة. تتداخل هذه الموجات وتتداخل بشكل بناء (خطوط مشرقة) ومدمرة (المناطق المظلمة). لا يمكننا رؤية ذلك إلا إذا سقط الضوء على الشاشة وانتشر في أعيننا. (ب) عندما يسقط الضوء الذي يمر عبر الشقوق المزدوجة على الشاشة، نرى نمطًا كهذا.

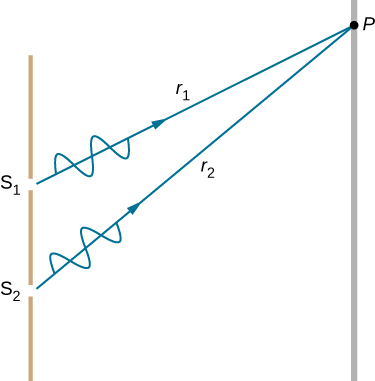
    لفهم نمط التداخل ذي الشق المزدوج، ضع في اعتبارك كيفية انتقال موجتين من الشقوق إلى الشاشة (الشكل\(\PageIndex{5}\)). كل شق هو مسافة مختلفة عن نقطة معينة على الشاشة. وبالتالي، تتناسب أعداد مختلفة من الأطوال الموجية مع كل مسار. تبدأ الموجات من الشقوق في الطور (من القمة إلى القمة)، ولكنها قد تنتهي خارج الطور (من القمة إلى القاع) عند الشاشة إذا اختلفت المسارات في الطول بمقدار نصف طول موجة، مما يؤدي إلى التداخل بشكل مدمر. إذا اختلفت المسارات بطول موجة كامل، فإن الموجات تصل في الطور (من القمة إلى القمة) إلى الشاشة، وتتداخل بشكل بناء. وبشكل عام، إذا كان فرق طول المسار\(\Delta l\) بين الموجتين هو أي عدد نصف متكامل من الأطوال الموجية [(1/2)، (3/2)، (5/2) ▼، وما إلى ذلك]، يحدث تداخل مدمر. وبالمثل، إذا كان فرق طول المسار هو أي عدد لا يتجزأ من الأطوال الموجية (، 2، 3، إلخ)، يحدث التداخل البنائي. يمكن التعبير عن هذه الشروط كمعادلات:

    \[\underbrace{\Delta l = m \lambda}_{\text{constructive interference}} \nonumber \]

    من أجل\(m = 0, \, ±1, \, ±2, \, ±3…\)

    \[\underbrace{\Delta l = \left(m + \frac{1}{2}\right)\lambda }_{\text{destructuve interference}} \nonumber \]

    من أجل\(m = 0, \, ±1, \, ±2, \, ±3…\)

    الصورة عبارة عن رسم تخطيطي يُظهر الموجات r1 و r2 التي تمر عبر الشقين S1 و S2. تلتقي الموجات في نقطة مشتركة P على الشاشة.
    الشكل\(\PageIndex{5}\): تتبع الموجات مسارات مختلفة من الشقوق إلى النقطة الشائعة P على الشاشة. يحدث التداخل المدمر عندما يكون أحد المسارات أطول بنصف طول موجة من الآخر - تبدأ الموجات في الطور ولكنها تخرج من الطور. يحدث التداخل البنائي عندما يكون أحد المسارات بطول موجة كامل أطول من الآخر - تبدأ الموجات وتصل في الطور.