1.2: انتشار الضوء
- Page ID
- 196634
في نهاية هذا القسم، ستكون قادرًا على:
- أوجد معامل الانكسار، بمعلومية سرعة الضوء في الوسط
- ضع قائمة بالطرق التي ينتقل بها الضوء من مصدر إلى موقع آخر
سرعة الضوء: القياسات المبكرة
أجرى عالم الفلك الدنماركي أولي رومر (1644-1710) أول قياس لسرعة الضوء في عام 1675. ودرس مدار أيو، أحد أقمار المشتري الأربعة الكبيرة، ووجد أنه شهد فترة ثورة بلغت 42.5 ساعة حول كوكب المشتري. كما اكتشف أن هذه القيمة تذبذبت بضع ثوان، اعتمادًا على موقع الأرض في مدارها حول الشمس. أدرك رويمر أن هذا التذبذب كان بسبب السرعة المحدودة للضوء ويمكن استخدامه لتحديد c.
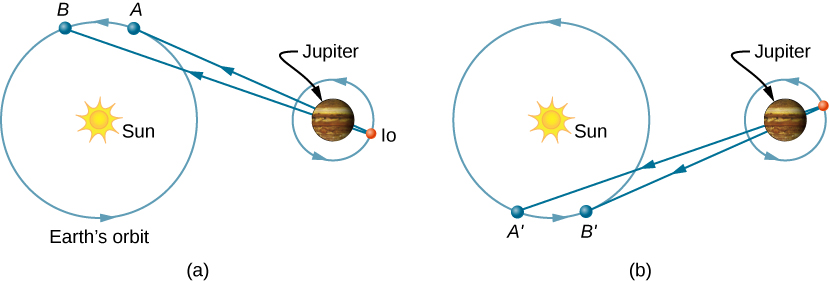
وجد رويمر فترة ثورة Io من خلال قياس الفترة الزمنية بين الكسوف المتتابع لكوكب المشتري. \(\PageIndex{1a}\)يوضح الشكل تكوينات الكواكب عندما يتم إجراء مثل هذا القياس من الأرض في جزء من مدارها حيث ينحسر عن كوكب المشتري. عندما تكون الأرض عند النقطة A، تتم محاذاة الأرض والمشتري وIo. في المرة التالية التي تحدث فيها هذه المحاذاة، تكون الأرض عند النقطة B، ويجب أن ينتقل الضوء الذي يحمل هذه المعلومات إلى الأرض إلى تلك النقطة. نظرًا لأن B أبعد عن المشتري عن A، يستغرق الضوء وقتًا أطول للوصول إلى الأرض عندما تكون الأرض عند B. تخيل الآن أنه بعد حوالي 6 أشهر، وتم ترتيب الكواكب كما في الشكل \(\PageIndex{1b}\). يبدأ قياس فترة Io بالأرض عند النقطة A وكسوف Io بواسطة المشتري. ثم يحدث الكسوف التالي عندما تكون الأرض عند النقطة B '، والتي يجب أن ينتقل إليها الضوء الذي يحمل معلومات هذا الكسوف. نظرًا لأن B 'أقرب إلى المشتري من A'، يستغرق الضوء وقتًا أقل للوصول إلى الأرض عندما يكون عند B'. وبالتالي فإن هذه الفترة الزمنية بين الكسوف المتتابع لـ Io التي تظهر في A و B هي أقل من الفترة الزمنية بين الكسوف المرئي في A و B. من خلال قياس الفرق في هذه الفترات الزمنية والمعرفة المناسبة بالمسافة بين المشتري والأرض، حسب رويمر أن سرعة الضوء كانت\(2.0 \times 10^8\,m/s\)، وهي أقل بنسبة 33٪ فقط من القيمة المقبولة اليوم.
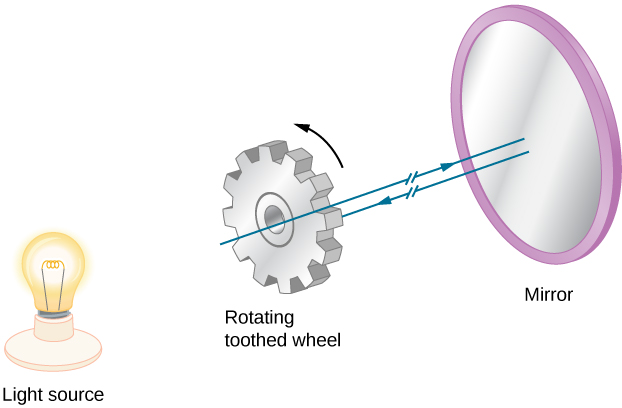
تم إجراء أول قياس أرضي ناجح لسرعة الضوء بواسطة أرماند فيزو (1819-1896) في عام 1849. لقد وضع عجلة مسننة يمكن تدويرها بسرعة كبيرة على قمة تل واحد ومرآة على قمة تل ثانية على بعد 8 كم (الشكل\(\PageIndex{2}\)). تم وضع مصدر ضوء مكثف خلف عجلة القيادة، بحيث عندما تدور العجلة، تقوم بتقطيع شعاع الضوء إلى سلسلة من النبضات. ثم تم ضبط سرعة العجلة حتى لا يعود أي ضوء إلى المراقب الموجود خلف العجلة. يمكن أن يحدث هذا فقط إذا كانت العجلة تدور بزاوية تقابل إزاحة الأسنان (n+½)، بينما تنتقل النبضات إلى المرآة والعكس. بمعرفة سرعة دوران العجلة وعدد الأسنان الموجودة على العجلة والمسافة إلى المرآة، حدد Fizeau سرعة الضوء لتكون\ (3.15\ مرات 10 ^ 8\، m/s\)، وهي نسبة مرتفعة جدًا بنسبة 5٪ فقط.
قام الفيزيائي الفرنسي جان برنارد ليون فوكو (1819-1868) بتعديل جهاز Fizeau باستبدال العجلة المسننة بمرآة دوارة. في عام 1862، قام بقياس سرعة الضوء لتكون 2.98×10 8 متر/ثانية، أي في حدود 0.6% من القيمة المقبولة حاليًا. استخدم ألبرت ميشيلسون (1852-1931) أيضًا طريقة فوكو في عدة مناسبات لقياس سرعة الضوء. أجريت تجاربه الأولى في عام 1878؛ وبحلول عام 1926، قام بتحسين هذه التقنية جيدًا لدرجة أنه وجد c (2.99796 ± 4) × 10 8 م/ث.
اليوم، أصبحت سرعة الضوء معروفة بدقة كبيرة. في الواقع، تعد سرعة الضوء في الفراغ c مهمة جدًا لدرجة أنها مقبولة كواحدة من الكميات الفيزيائية الأساسية ولها القيمة
\ [c=2.99792458\ مرات 10 ^ 8 متر/ثانية\ تساوي 3.00\ مرات 10 ^ 8 م/ث \ التسمية {السرعة}\]
حيث يتم استخدام القيمة التقريبية 3.00×10 8 m/s عندما تكون الدقة المكونة من ثلاثة أرقام كافية.
سرعة الضوء في المادة
سرعة الضوء عبر المادة أقل مما هي عليه في الفراغ، لأن الضوء يتفاعل مع الذرات في المادة. تعتمد سرعة الضوء بشدة على نوع المادة، حيث يختلف تفاعلها مع الذرات المختلفة والشبكات البلورية والبنى التحتية الأخرى. يمكننا تحديد ثابت لمادة تصف سرعة الضوء فيها، ويسمى مؤشر الانكسار n:
\[n=\dfrac{c}{v} \label{index} \]
\(v\)أين سرعة الضوء المرصودة في المادة.
نظرًا لأن سرعة الضوء دائمًا أقل من c في المادة وتساوي c فقط في الفراغ، يكون معامل الانكسار دائمًا أكبر من أو يساوي واحد؛ أي n≥1. \(\PageIndex{1}\)يعطي الجدول مؤشرات الانكسار لبعض المواد التمثيلية. يتم سرد القيم لطول موجة معين من الضوء، لأنها تختلف قليلاً مع الطول الموجي. (يمكن أن يكون لهذا تأثيرات مهمة، مثل الألوان المفصولة بالمنشور، كما سنرى في التشتت.) لاحظ أنه بالنسبة للغازات، يكون n قريبًا من 1.0. يبدو هذا معقولًا، حيث يتم فصل الذرات في الغازات على نطاق واسع، وينتقل الضوء عند درجة مئوية في الفراغ بين الذرات. من الشائع تناول\(n=1\) الغازات ما لم تكن هناك حاجة إلى دقة كبيرة. على الرغم من أن سرعة الضوء v في الوسط تختلف اختلافًا كبيرًا عن قيمته c في الفراغ، إلا أنها لا تزال سرعة كبيرة.
مثال\(\PageIndex{1}\): سرعة الضوء في المجوهرات
احسب سرعة الضوء في الزركون، وهو مادة تستخدم في المجوهرات لتقليد الماس.
إستراتيجية
يمكننا حساب سرعة الضوء في مادة ما\(v\) من معامل انكسار\(n\) المادة، باستخدام المعادلة \ الحمراء {index}
الحل
إعادة ترتيب المعادلة\ ref {index} لـ\(v\) يعطينا
\[v=\dfrac{c}{n}. \nonumber \]
معامل الانكسار للزركون هو 1.923 في الجدول \(\PageIndex{1}\)،\(c\) ويرد في المعادلة\ ref {speed}. يؤدي إدخال هذه القيم في المعادلة إلى:
\ [\ ابدأ {محاذاة *} v &=\ dfrac {3.00×10^8m/s} {1.923}\\ [4pt] &=1.56×10^8m/ثانية.\ النهاية {محاذاة}\ لا يوجد رقم\]
الدلالة
هذه السرعة أكبر قليلاً من نصف سرعة الضوء في الفراغ ولا تزال عالية مقارنة بالسرعات التي نمر بها عادةً . المادة الوحيدة المدرجة في الجدول\(\PageIndex{1}\) التي لها معامل انكسار أكبر من الزركون هي الماس. سنرى لاحقًا أن معامل الانكسار الكبير للزركون يجعله يتألق أكثر من الزجاج، ولكن أقل من الماس.
\(\PageIndex{1}\)يوضح الجدول أن الإيثانول والمياه العذبة لهما مؤشرات انكسار متشابهة جدًا. ما النسبة المئوية التي تختلف بها سرعات الضوء في هذه السوائل؟
- إجابة
-
2.1% (إلى رقمين مهمين)
نموذج راي للضوء
لقد درست بالفعل بعض الخصائص الموجية للضوء في الفصل السابق عن الموجات الكهرومغناطيسية. في هذا الفصل، نبدأ بشكل أساسي بخصائص الأشعة. هناك ثلاث طرق يمكن للضوء من خلالها الانتقال من مصدر إلى موقع آخر (الشكل \(\PageIndex{1}\)). يمكن أن تأتي مباشرة من المصدر من خلال مساحة فارغة، مثل من الشمس إلى الأرض. أو يمكن للضوء أن ينتقل عبر وسائط مختلفة، مثل الهواء والزجاج، إلى المراقب. يمكن أن يصل الضوء أيضًا بعد الانعكاس، مثل المرآة. في كل هذه الحالات، يمكننا تمثيل مسار الضوء كخط مستقيم يسمى الشعاع.
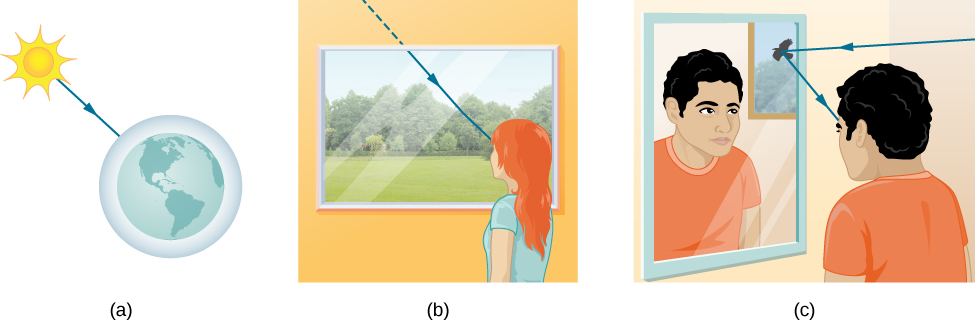
تُظهر التجارب أنه عندما يتفاعل الضوء مع جسم أكبر بعدة مرات من طوله الموجي، فإنه ينتقل في خطوط مستقيمة ويعمل مثل الشعاع. لا تظهر خصائص الموجة الخاصة بها في مثل هذه الحالات. نظرًا لأن الطول الموجي للضوء المرئي أقل من ميكرون (جزء من ألف من المليمتر)، فإنه يعمل مثل الشعاع في العديد من الحالات الشائعة التي يصادف فيها أجسامًا أكبر من ميكرون. على سبيل المثال، عندما يواجه الضوء المرئي أي شيء كبير بما يكفي بحيث يمكننا ملاحظته بعيون غير مساعدة، مثل العملة، فإنه يعمل مثل الشعاع، بخصائص موجية ضئيلة بشكل عام.
في كل هذه الحالات، يمكننا نمذجة مسار الضوء كخطوط مستقيمة. قد يغير الضوء اتجاهه عندما يواجه أشياء (مثل المرآة) أو عند مروره من مادة إلى أخرى (مثل المرور من الهواء إلى الزجاج)، ولكنه يستمر بعد ذلك في خط مستقيم أو كشعاع. تأتي كلمة «ray» من الرياضيات وتعني هنا خطًا مستقيمًا ينشأ في مرحلة ما. من المقبول تصور أشعة الضوء كأشعة ليزر. يصف نموذج أشعة الضوء مسار الضوء كخطوط مستقيمة.
نظرًا لأن الضوء يتحرك في خطوط مستقيمة، ويغير الاتجاهات عندما يتفاعل مع المواد، فإن مساره يوصف بالهندسة وعلم المثلثات البسيط. لذلك يُطلق على هذا الجزء من البصريات، حيث يهيمن جانب أشعة الضوء، اسم البصريات الهندسية. هناك قانونان يحكمان كيفية تغيير الضوء لاتجاهه عندما يتفاعل مع المادة. هذا هو قانون الانعكاس، للحالات التي يرتد فيها الضوء عن المادة، وقانون الانكسار، للحالات التي يمر فيها الضوء عبر المادة. سوف ندرس المزيد حول كل من هذه القوانين في الأقسام القادمة من هذا الفصل.


