1.3: الوحدات والمعايير

Last updated
Save as PDF

Page ID: 199972

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

وصف كيفية تعريف وحدات SI الأساسية.
وصف كيفية إنشاء الوحدات المشتقة من الوحدات الأساسية.
قم بالتعبير عن الكميات المعطاة بوحدات SI باستخدام البادئات المترية.

كما رأينا سابقًا، فإن نطاق الأشياء والظواهر التي تمت دراستها في الفيزياء هائل. من العمر القصير للغاية للنواة إلى عمر الأرض، من الأحجام الصغيرة للجسيمات دون النووية إلى المسافة الشاسعة إلى حواف الكون المعروف، من القوة التي يمارسها البرغوث القافز إلى القوة بين الأرض والشمس، هناك عوامل كافية بمقدار 10 لتحدي خيال حتى أكثر العلماء خبرة. إن إعطاء القيم العددية للكميات الفيزيائية والمعادلات للمبادئ الفيزيائية يسمح لنا بفهم الطبيعة بشكل أعمق بكثير من الأوصاف النوعية وحدها. لفهم هذه النطاقات الواسعة، يجب أن يكون لدينا أيضًا وحدات مقبولة للتعبير عنها. سنجد أنه حتى في المناقشة العادية المحتملة للعدادات والكيلوغرامات والثواني، تظهر بساطة عميقة للطبيعة: يمكن التعبير عن جميع الكميات الفيزيائية كمجموعات من سبع كميات فيزيائية أساسية فقط.

نحدد الكمية المادية إما عن طريق تحديد كيفية قياسها أو من خلال تحديد كيفية حسابها من القياسات الأخرى. على سبيل المثال، قد نحدد المسافة والوقت من خلال تحديد طرق قياسهما، مثل استخدام عصا القياس وساعة التوقيت. بعد ذلك، يمكننا تحديد متوسط السرعة من خلال الإشارة إلى أنه يتم حسابه على أنه المسافة الإجمالية المقطوعة مقسومًا على وقت السفر.

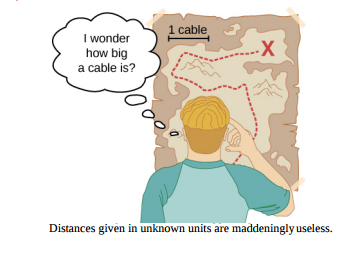
يتم التعبير عن قياسات الكميات الفيزيائية من حيث الوحدات، وهي قيم موحدة. على سبيل المثال، يمكن التعبير عن طول السباق، وهو عبارة عن كمية مادية، بوحدات الأمتار (للعدائين) أو الكيلومترات (لعدائي المسافات). بدون وحدات معيارية، سيكون من الصعب للغاية على العلماء التعبير عن القيم المقاسة ومقارنتها بطريقة ذات معنى (الشكل\(\PageIndex{1}\)).

رسم لشخص ينظر إلى خريطة تحمل مقياس المسافة المسمى ككبل واحد ويتساءل عن حجم الكبل. — الشكل\(\PageIndex{1}\): المسافات المعطاة بوحدات غير معروفة عديمة الفائدة بشكل جنوني.

يتم استخدام نظامين رئيسيين من الوحدات في العالم: وحدات SI (للنظام الفرنسي الدولي للوحدة)، المعروف أيضًا باسم النظام المتري، والوحدات الإنجليزية (المعروفة أيضًا باسم النظام العرفي أو الإمبراطوري). تم استخدام الوحدات الإنجليزية تاريخيًا في الدول التي كانت تحكمها الإمبراطورية البريطانية ولا تزال تستخدم على نطاق واسع في الولايات المتحدة. يمكن أيضًا الإشارة إلى الوحدات الإنجليزية بنظام foot-pound-cond (fps)، بدلاً من نظام السنتيمتر - غرام - الثانية (cgs). قد تصادف أيضًا مصطلح وحدات SAE، الذي سمي على اسم جمعية مهندسي السيارات. يُشار إلى المنتجات مثل أدوات التثبيت وأدوات السيارات (على سبيل المثال، مفاتيح الربط) التي يتم قياسها بالبوصة بدلاً من الوحدات المترية باسم مثبتات SAE أو مفاتيح SAE.

تقريبًا كل بلد آخر في العالم (باستثناء الولايات المتحدة) يستخدم الآن وحدات SI كمعيار. النظام المتري هو أيضًا النظام القياسي المتفق عليه من قبل العلماء وعلماء الرياضيات.

وحدات SI: الوحدات الأساسية والمستمدة

في أي نظام من الوحدات، يجب تحديد وحدات بعض الكميات الفيزيائية من خلال عملية قياس. تسمى هذه الكميات الأساسية لهذا النظام ووحداتها هي الوحدات الأساسية للنظام. يمكن بعد ذلك التعبير عن جميع الكميات الفيزيائية الأخرى كمجموعات جبرية للكميات الأساسية. ثم تُعرف كل من هذه الكميات الفيزيائية بالكمية المشتقة وتسمى كل وحدة وحدة وحدة مشتقة. يعد اختيار الكميات الأساسية تعسفيًا إلى حد ما، طالما أنها مستقلة عن بعضها البعض ويمكن اشتقاق جميع الكميات الأخرى منها. عادةً ما يكون الهدف هو اختيار الكميات المادية التي يمكن قياسها بدقة بدقة عالية مثل الكميات الأساسية. السبب في ذلك بسيط. نظرًا لأنه يمكن التعبير عن الوحدات المشتقة كتركيبات جبرية للوحدات الأساسية، فلا يمكن أن تكون دقيقة ودقيقة إلا مثل الوحدات الأساسية التي اشتقت منها.

بناءً على هذه الاعتبارات، توصي منظمة المعايير الدولية باستخدام سبع كميات أساسية تشكل النظام الدولي للكميات (ISQ). هذه هي الكميات الأساسية المستخدمة لتعريف وحدات SI الأساسية. \(\PageIndex{1}\)يسرد الجدول هذه الكميات الأساسية السبعة لـ ISQ والوحدات الأساسية لـ SI المقابلة.

الجدول\(\PageIndex{1}\): الكميات الأساسية لـ ISQ ووحدات SI الخاصة بها
كمية ISQ الأساسية	وحدة قاعدة SI
الطول	متر (م)
الكتلة	كيلوغرام (كجم)
الوقت	ثانية (ثانية)
تيار كهربي	أمبير (A)
درجة حرارة الديناميكا الحرارية	كلفن (K)
كمية المادة	مول (مول)
كثافة الإضاءة	كانديلا (سي دي)

ربما تكون على دراية بالفعل ببعض الكميات المشتقة التي يمكن تشكيلها من الكميات الأساسية في الجدول\(\PageIndex{1}\). على سبيل المثال، يتم حساب المفهوم الهندسي للمنطقة دائمًا كمنتج لطولين. وبالتالي، فإن المساحة هي كمية مشتقة يمكن التعبير عنها بوحدات SI الأساسية باستخدام الأمتار المربعة (m x m = m ²). وبالمثل، فإن الحجم هو كمية مشتقة يمكن التعبير عنها بالمتر المكعب (m ³). السرعة هي الطول لكل مرة؛ لذلك من حيث وحدات SI الأساسية، يمكننا قياسها بالأمتار في الثانية (م/ث). كثافة كتلة الحجم (أو الكثافة فقط) هي الكتلة لكل حجم، والتي يتم التعبير عنها بوحدات SI الأساسية مثل الكيلوجرام لكل متر مكعب (kg/m ³). يمكن أيضًا اعتبار الزوايا ككميات مشتقة لأنه يمكن تعريفها على أنها نسبة طول القوس المقابل بنصف قطر الدائرة إلى نصف قطر الدائرة. هذه هي الطريقة التي يتم بها تعريف الراديان. اعتمادًا على خلفيتك واهتماماتك، قد تتمكن من التوصل إلى كميات مشتقة أخرى، مثل معدل تدفق الكتلة (كجم/ثانية) أو معدل تدفق الحجم (م ^3/s) للسائل، والشحنة الكهربائية (A • s)، وكثافة تدفق الكتلة [kg/ (m ² • s)]، وما إلى ذلك. سنرى العديد من الأمثلة في هذا النص. في الوقت الحالي، تكمن النقطة في أنه يمكن اشتقاق كل كمية فيزيائية من الكميات الأساسية السبع في الجدول\(\PageIndex{1}\)، ويمكن اشتقاق وحدات كل كمية فيزيائية من وحدات SI الأساسية السبع.

بالنسبة للجزء الأكبر، نستخدم وحدات SI في هذا النص. تُستخدم الوحدات غير SI في عدد قليل من التطبيقات التي يشيع استخدامها فيها، مثل قياس درجة الحرارة بالدرجات المئوية (° C)، وقياس حجم السائل باللترات (L)، وقياس طاقات الجسيمات الأولية في الإلكترون فولت (eV). عندما تتم مناقشة الوحدات غير الخاصة بـ SI، يتم ربطها بوحدات SI من خلال التحويلات. على سبيل المثال، 1 لتر يساوي 10 ⁻³ م ³.

تحقق من مصدر شامل للمعلومات حول وحدات SI في مرجع المعهد الوطني للمعايير والتكنولوجيا (NIST) حول الثوابت والوحدات وعدم اليقين.

وحدات الوقت والطول والكتلة: الثانية والمتر والكيلوجرام

تهتم الفصول الأولية في هذا النص بالميكانيكا والسوائل والأمواج. في هذه الموضوعات، يمكن التعبير عن جميع الكميات الفيزيائية ذات الصلة من حيث الوحدات الأساسية للطول والكتلة والوقت. لذلك، ننتقل الآن إلى مناقشة هذه الوحدات الأساسية الثلاث، مع ترك مناقشة الوحدات الأخرى حتى يتم الاحتياج إليها لاحقًا.

الثانية

وحدة SI للوقت، الثانية (المختصرة)، لها تاريخ طويل. لسنوات عديدة تم تعريفه على أنه 1/86400 من متوسط اليوم الشمسي. في الآونة الأخيرة، تم اعتماد معيار جديد للحصول على دقة أكبر ولتحديد الثاني من حيث ظاهرة فيزيائية غير متغيرة أو ثابتة (لأن اليوم الشمسي يزداد طولًا نتيجة التباطؤ التدريجي جدًا في دوران الأرض). يمكن جعل ذرات السيزيوم تهتز بطريقة ثابتة للغاية، ويمكن ملاحظة هذه الاهتزازات بسهولة وإحصائها. في عام 1967، تم إعادة تعريف الثانية على أنها الوقت اللازم لحدوث 9,192,631,770 من هذه الاهتزازات (الشكل\(\PageIndex{2}\)). لاحظ أن هذا قد يبدو أكثر دقة مما قد تحتاجه في أي وقت مضى، ولكنه ليس كذلك - تعتمد أجهزة تحديد المواقع على دقة الساعات الذرية لتتمكن من إعطائك توجيهات خطوة بخطوة على سطح الأرض، بعيدًا عن الأقمار الصناعية التي تبث موقعها.

منظر علوي لنافورة ذرية. — الشكل\(\PageIndex{2}\): تستخدم الساعة الذرية مثل هذه اهتزازات ذرات السيزيوم للحفاظ على دقة الوقت بشكل أفضل من ميكروثانية في السنة. تعتمد الوحدة الأساسية للوقت، الثانية، على مثل هذه الساعات. تبدو هذه الصورة لأسفل من أعلى نافورة ذرية يبلغ ارتفاعها 30 قدمًا تقريبًا. (تصوير: ستيف جورفيتسون)

ذا ميتر

وحدة SI للطول هي العداد (اختصار m)؛ كما تغير تعريفه بمرور الوقت ليصبح أكثر دقة. تم تعريف المقياس لأول مرة في عام 1791 على أنه 1/10,000,000 من المسافة من خط الاستواء إلى القطب الشمالي. تم تحسين هذا القياس في عام 1889 من خلال إعادة تعريف العداد ليكون المسافة بين خطين محفورين على شريط بلاتينيوم - إيريديوم محفوظ الآن بالقرب من باريس. بحلول عام 1960، أصبح من الممكن تحديد المقياس بشكل أكثر دقة من حيث الطول الموجي للضوء، لذلك تم إعادة تعريفه مرة أخرى على أنه 1,650,763.73 أطوال موجية من الضوء البرتقالي المنبعث من ذرات الكريبتون. في عام 1983، تم إعطاء المقياس تعريفه الحالي (جزئيًا لمزيد من الدقة) حيث ينتقل الضوء المسافة في الفراغ في 1/299,792,458 من الثانية (الشكل\(\PageIndex{3}\)). جاء هذا التغيير بعد معرفة سرعة الضوء التي تبلغ بالضبط 299.792.458 متر/ثانية، وسيتغير طول العداد إذا تم قياس سرعة الضوء يومًا ما بدقة أكبر.

رسم لعصا عداد ومصباح يضيء شعاعًا من الضوء. يشير السهم إلى أن الشعاع يمتد بطول عصا العداد. يُطلق على الرسم اسم «ينتقل الضوء لمسافة متر واحد في 1 خلال 299,792,458 ثانية. — الشكل\(\PageIndex{3}\): يُعرّف المقياس بأنه المسافة التي يقطعها الضوء في 1/299,792,458 من الثانية في الفراغ. المسافة المقطوعة هي السرعة مضروبة في الوقت.

ذا كيلوجرام

وحدة SI للكتلة هي الكيلوغرام (كجم المختصر)؛ من 1795 إلى 2018 تم تعريفها على أنها كتلة أسطوانة بلاتينيوم-إيريديوم محفوظة بمعيار العداد القديم في المكتب الدولي للأوزان والمقاييس بالقرب من باريس. ومع ذلك، فقد فقدت هذه الأسطوانة ما يقرب من 50 ميكروغرامًا منذ إنشائها. نظرًا لأن هذا هو المعيار، فقد أدى هذا إلى تغيير طريقة تعريفنا للكيلوغرام. لذلك، تم اعتماد تعريف جديد في مايو 2019 استنادًا إلى ثابت بلانك والثوابت الأخرى التي لن تتغير أبدًا في القيمة. سوف ندرس ثابت بلانك في ميكانيكا الكم، وهو مجال من الفيزياء يصف كيفية عمل أصغر قطع الكون. يتم قياس الكيلوغرام على ميزان كيبل (انظر\(\PageIndex{4}\)). عندما يتم وضع وزن على ميزان كيبل، يتم إنتاج تيار كهربائي يتناسب مع ثابت بلانك. وبما أن ثابت بلانك محدد، فإن القياسات الحالية الدقيقة في الميزان تحدد الكيلوغرام.

الشكل\(\PageIndex{4}\): إعادة تعريف وحدة SI للكتلة. ميزان Kibble التابع للمعهد الوطني الأمريكي للمعايير والتكنولوجيا هو آلة توازن وزن كتلة الاختبار مع التيار الكهربائي الناتج المطلوب لقوة لموازنتها.

البادئات المترية

تعد وحدات SI جزءًا من النظام المتري، وهو مناسب للحسابات العلمية والهندسية لأن الوحدات مصنفة حسب عوامل 10. \(\PageIndex{1}\)يسرد الجدول البادئات المترية والرموز المستخدمة للإشارة إلى عوامل مختلفة من 10 في وحدات SI. على سبيل المثال، السنتيمتر هو جزء من مائة متر (بالرموز، 1 سم = 10 ^—2 م) والكيلومتر هو ألف متر (1 كم = 10 ³ م). وبالمثل، فإن الميغرام هو مليون جرام (1 مجم = 10 ⁶ جم)، والنانو ثانية هو جزء من مليار من الثانية (1 نانوثانية = 10 ^—9 ثانية)، والمقياس التيراميتر هو تريليون متر (1 طن متري = 10 ¹² م).

جدول\(\PageIndex{2}\): البادئات المترية لقوى العدد ١٠ ورموزها
بادئة	الرمز	المعنى	بادئة	الرمز	المعنى
يوتا-	ص	10 ²⁴	يوكتو-	ص	10 ^- ²⁴
زيتا-	ض	10 ²¹	زيبتو-	ض	10 ^- ²¹
امتحان-	ه	10 ¹⁸	كاتو-	ه	10 ^-18
بيتا-	ص	10 ¹⁵	فيمتو-	ص	10 ^-15
تيرا-	إلى	10 ¹²	بيكو-	إلى	10 ^-12
جيجا-	ز	10 ⁹	نانو-	ز	10 ^-9
ميجا-	م	10 ⁶	مايكرو-	م	10 ^-6
كيلو-	ك	10 ³	ميلي-	ك	10 ^-3
هيكتو-	ح	10 ²	سنتي-	ح	10 ^-2
ديكا-	دا	10 ¹	ديسي-	دا	10 ^-1

القاعدة الوحيدة عند استخدام البادئات المترية هي أنه لا يمكنك «مضاعفتها». على سبيل المثال، إذا كانت لديك قياسات بمقاييس البيتامترات (1 Pm = 10 ¹⁵ m)، فليس من المناسب التحدث عن المقاييس الضخمة، على الرغم من أن 10 ⁶ × 10 ⁹ = 10 ¹⁵. في الممارسة العملية، المرة الوحيدة التي يصبح فيها هذا مربكًا بعض الشيء هي عند مناقشة الجماهير. كما رأينا، وحدة كتلة SI الأساسية هي الكيلوغرام (kg)، ولكن يجب تطبيق البادئات المترية على الجرام (g)، لأنه لا يُسمح لنا بـ «مضاعفة» البادئات. وهكذا، يتم كتابة ألف كيلوغرام (10 ^{- 3} كجم) في صورة ميغرام (1 ملغ) منذ ذلك الحين

\[10^{3}\; kg = 10^{3} \times 10^{3}\; g = 10^{6}\; g = 1\; Mg \ldotp\]

بالمناسبة، يُطلق على 10 ³ كجم أيضًا اسم الطن المتري، ويتم اختصاره بـ t، وهي إحدى الوحدات خارج نظام SI التي تعتبر مقبولة للاستخدام مع وحدات SI.

كما نرى في القسم التالي، تتمتع الأنظمة المترية بميزة أن تحويلات الوحدات تنطوي فقط على قوى 10. هناك 100 سم في 1 متر، 1000 متر في 1 كم، وهلم جرا. في الأنظمة غير المترية، مثل نظام الوحدات الإنجليزي، لا تكون العلاقات بهذه البساطة - فهناك 12 بوصة في 1 قدم، و5280 قدمًا في 1 ميل، وهكذا.

ميزة أخرى للأنظمة المترية هي أنه يمكن استخدام نفس الوحدة على نطاقات كبيرة جدًا من القيم ببساطة عن طريق تحجيمها باستخدام بادئة مترية مناسبة. يتم اختيار البادئة بترتيب حجم الكميات الفيزيائية الشائعة في المهمة قيد البحث. على سبيل المثال، تعتبر المسافات بالأمتار مناسبة في البناء، في حين أن المسافات بالكيلومترات مناسبة للسفر الجوي، والنانومتر ملائمة في التصميم البصري. مع النظام المتري، ليست هناك حاجة لابتكار وحدات جديدة لتطبيقات معينة. بدلاً من ذلك، نقوم بإعادة قياس الوحدات التي نعرفها بالفعل.

مثال\(\PageIndex{1}\): Using Metric Prefixes

أعد تحديد الكتلة 1.93 × 10 ¹³ kg باستخدام بادئة مترية بحيث تكون القيمة العددية الناتجة أكبر من واحد ولكن أقل من 1000.

إستراتيجية

نظرًا لأنه لا يُسمح لنا بـ «مضاعفة» البادئات، نحتاج أولاً إلى إعادة صياغة الكتلة بالجرام عن طريق استبدال رمز البادئة k بعامل 10 ³ (الجدول\(\PageIndex{2}\)). بعد ذلك، يجب أن نرى أي البادئات في الجدول\(\PageIndex{2}\) هي الأقرب إلى القوة الناتجة وهي 10 عند كتابة الرقم بالتدوين العلمي. نحن نستخدم أيًا من هاتين البادئتين يعطينا رقمًا بين واحد و 1000.

الحل

باستبدال k بالكيلوغرام بعامل 10 ³، نجد ذلك

\[1.93 \times 10^{13}\; kg = 1.93 \times 10^{13} \times 10^{3}\; g = 1.93 \times 10^{16}\; g \ldotp \nonumber\]

من الجدول\(\PageIndex{2}\)، نرى أن 10 ^{16 تقع} بين «peta-» (10 ¹⁵) و «exa-» (10 ¹⁸). إذا استخدمنا بادئة «peta-»، فسنجد أن 1.93 × 10 ¹⁶ g = 1.93 × 10 ¹ Pg، لأن 16 = 1 + 15. بدلاً من ذلك، إذا استخدمنا بادئة «exa-» نجد أن 1.93 × 10 ¹⁶ g = 1.93 × 10 ^{−2 Eg}، لأن 16 = −2 + 18. نظرًا لأن المشكلة تتطلب القيمة العددية بين واحد و 1000، فإننا نستخدم بادئة «peta-» والإجابة هي 19.3 Pg.

الدلالة

من السهل ارتكاب أخطاء حسابية سخيفة عند التبديل من بادئة إلى أخرى، لذلك من الجيد دائمًا التحقق من تطابق إجابتنا النهائية مع الرقم الذي بدأنا به. طريقة سهلة للقيام بذلك هي وضع كلا الرقمين في الترميز العلمي وقوى العد 10، بما في ذلك تلك المخفية في البادئات. إذا لم نخطئ، يجب أن تتطابق قوى 10. في هذه المشكلة، بدأنا بـ 1.93 × 10 ¹³ كجم، لذلك لدينا 13 + 3 = 16 قوة من 10. إجابتنا النهائية في الترميز العلمي هي 1.93 × 10 ¹ Pg، لذلك لدينا 1 + 15 = 16 قوة من 10. لذلك، يتم فحص كل شيء.

إذا نشأت هذه الكتلة من الحساب، فإننا نرغب أيضًا في التحقق لتحديد ما إذا كانت الكتلة بهذا الحجم لها أي معنى في سياق المشكلة. لهذا، قد يكون الشكل 1.4 مفيدًا.

التمارين\(\PageIndex{1}\)

أعد صياغة 4.79 × 10 ⁵ كجم باستخدام بادئة مترية بحيث يكون الرقم الناتج أكبر من واحد ولكن أقل من 1000.

إجابة: أضف نصوصًا هنا. لا تحذف هذا النص أولاً.