5.6: تأثير دوبلر
- Page ID
- 197298
أهداف التعلم
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح لماذا ستتغير الخطوط الطيفية للفوتونات التي نلاحظها من جسم نتيجة لحركة الجسم نحونا أو بعيدًا عنا
- وصف كيف يمكننا استخدام تأثير دوبلر لاستنتاج كيفية تحرك الأجسام الفلكية عبر الفضاء
قدم لك القسمان الأخيران العديد من المفاهيم الجديدة، ونأمل أن ترى من خلال ذلك فكرة رئيسية واحدة تظهر. يمكن لعلماء الفلك التعرف على العناصر الموجودة في النجوم والمجرات من خلال فك تشفير المعلومات في خطوطها الطيفية. ومع ذلك، هناك عامل معقد في تعلم كيفية فك شفرة رسالة ضوء النجوم. إذا كان النجم يتحرك نحونا أو بعيدًا عنا، فستكون خطوطه في مكان مختلف قليلاً في الطيف عن المكان الذي ستكون فيه في النجم أثناء الراحة. ومعظم الأجسام في الكون لديها بعض الحركة بالنسبة للشمس.
تؤثر الحركة على الموجات
في عام 1842، قام كريستيان دوبلر أولاً بقياس تأثير الحركة على الأمواج من خلال استئجار مجموعة من الموسيقيين للعب على عربة سكة حديد مفتوحة أثناء تحركها على طول المسار. ثم طبق ما تعلمه على جميع الموجات، بما في ذلك الضوء، وأشار إلى أنه إذا كان مصدر الضوء يقترب أو ينحسر من الراصد، فإن موجات الضوء ستكون، على التوالي، مزدحمة بشكل أوثق أو منتشرة. المبدأ العام، المعروف الآن باسم تأثير دوبلر، موضح في الشكل\(\PageIndex{1}\).
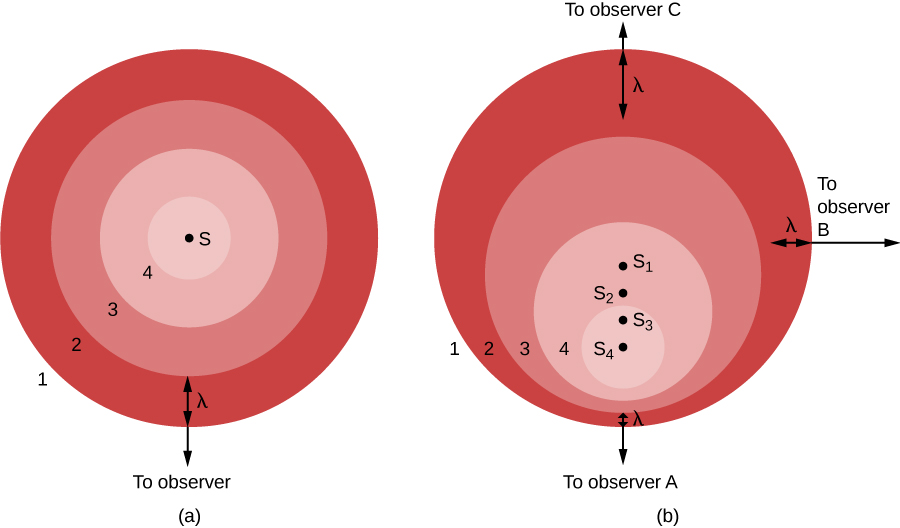
في الشكل\(\PageIndex{1a}\)، يكون مصدر الضوء (S) في حالة سكون بالنسبة للمراقب. يعطي المصدر سلسلة من الموجات، التي قمنا بتسمية قممها 1 و 2 و 3 و 4. تنتشر موجات الضوء بالتساوي في جميع الاتجاهات، مثل التموجات من رذاذ الماء في البركة. يتم فصل القمم بمسافة،، حيث هو الطول الموجي. يرى الراصد، الذي يقع في اتجاه الجزء السفلي من الصورة، موجات الضوء تقترب بشكل جميل ومتساوي، بفارق طول موجي واحد. سيرى المراقبون الموجودون في أي مكان آخر نفس الشيء.
من ناحية أخرى، إذا كان مصدر الضوء يتحرك بالنسبة للمراقب، كما هو موضح في الشكل\(\PageIndex{1b}\)، فإن الموقف أكثر تعقيدًا. بين الوقت الذي تنبعث فيه إحدى الشعارات وتكون العلامة التالية جاهزة للخروج، تحرك المصدر قليلاً نحو أسفل الصفحة. من وجهة نظر الراصد أ، أدت حركة المصدر هذه إلى تقليل المسافة بين القمم - إنها تضغط على القمم معًا، كما قد يقول هذا المراقب.
في الشكل\(\PageIndex{1b}\)، نعرض الموقف من منظور ثلاثة مراقبين. يظهر المصدر في أربعة مواضع، وهي\(S_1\)\(S_2\)،\(S_3\)،\(S_4\)، وكل منها يتوافق مع انبعاث قمة موجة واحدة. بالنسبة للمراقب A، يبدو أن الموجات تتبع بعضها البعض عن كثب، بطول موجة منخفض وبالتالي زيادة التردد. (تذكر أن جميع موجات الضوء تنتقل بسرعة الضوء عبر الفضاء الفارغ، بغض النظر عن السبب. هذا يعني أن الحركة لا يمكن أن تؤثر على السرعة، ولكن فقط على الطول الموجي والتردد. مع انخفاض الطول الموجي، يجب زيادة التردد. إذا كانت الموجات أقصر، فسيتمكن المزيد من التحرك خلال كل ثانية.)
الوضع ليس هو نفسه بالنسبة للمراقبين الآخرين. دعونا ننظر إلى الموقف من وجهة نظر المراقب C، الموجود مقابل المراقب A في الشكل\(\PageIndex{1}\). بالنسبة لها، فإن المصدر يبتعد عن موقعها. ونتيجة لذلك، لا يتم ضغط الموجات معًا ولكن بدلاً من ذلك تنتشر بحركة المصدر. تصل القمم بطول موجة متزايد وتردد منخفض. بالنسبة للمراقب B، في اتجاه بزاوية قائمة لحركة المصدر، لم يُلاحظ أي تأثير. يظل الطول الموجي والتردد كما كانا في الجزء (أ) من الشكل.
يمكننا أن نرى من هذا الرسم التوضيحي أن تأثير دوبلر ينتج فقط عن طريق حركة باتجاه الراصد أو بعيدًا عنه، وهي حركة تسمى السرعة الشعاعية. الحركة الجانبية لا تنتج مثل هذا التأثير. سيلاحظ المراقبون بين A و B بعض تقصير موجات الضوء لهذا الجزء من حركة المصدر الذي يقع على طول خط رؤيتهم. سيلاحظ المراقبون بين B و C إطالة موجات الضوء الموجودة على طول خط رؤيتهم.
ربما سمعت تأثير دوبلر بموجات صوتية. عندما تقترب منك صافرة القطار أو صفارات الشرطة ثم تبتعد، ستلاحظ انخفاضًا في درجة الصوت (وهي الطريقة التي تفسر بها الحواس البشرية تردد الموجة الصوتية) للموجات الصوتية. مقارنة بالموجات أثناء الراحة، فقد تغيرت من أكثر تكرارًا قليلاً عند القدوم نحوك، إلى أقل تكرارًا قليلاً عند الابتعاد عنك.
يمكن سماع مثال جميل لهذا التغيير في صوت صافرة القطار في نهاية أغنية Beach Boys الكلاسيكية «Caroline, No» على ألبومهم Pet Sounds. لسماع هذا الصوت، انتقل إلى إصدار YouTube هذا من الأغنية. يبدأ صوت القطار في حوالي الساعة 2:20.
تحولات اللون
عندما يتحرك مصدر الموجات نحوك، ينخفض الطول الموجي قليلاً. إذا كانت الموجات المعنية عبارة عن ضوء مرئي، فإن ألوان الضوء تتغير قليلاً. مع انخفاض الطول الموجي، فإنها تتحول نحو الطرف الأزرق من الطيف: يسمي علماء الفلك هذا التحول الأزرق (نظرًا لأن نهاية الطيف بنفسجية حقًا، فمن المحتمل أن يكون المصطلح هو التحول البنفسجي، لكن اللون الأزرق هو اللون الأكثر شيوعًا). عندما يبتعد المصدر عنك ويصبح الطول الموجي أطول، فإننا نسمي التغيير في الألوان باللون الأحمر. نظرًا لاستخدام تأثير دوبلر لأول مرة مع الضوء المرئي في علم الفلك، أصبح مصطلحا «التحول الأزرق» و «الانزياح الأحمر» راسخين جيدًا. اليوم، يستخدم علماء الفلك هذه الكلمات لوصف التغيرات في الأطوال الموجية للموجات الراديوية أو الأشعة السينية بشكل مريح كما يستخدمونها لوصف التغيرات في الضوء المرئي.
كلما زادت الحركة نحونا أو بعيدًا عنا، زاد تحول دوبلر. إذا كانت الحركة النسبية على طول خط الرؤية بالكامل، فإن صيغة تحول دوبلر للضوء هي
\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]
أين\(\lambda\) الطول الموجي المنبعث من المصدر،\(\Delta \lambda\) هو الفرق\(\lambda\) بين الطول الموجي الذي يقيسه\(c\) الراصد،\(v\) هو سرعة الضوء، وهو السرعة النسبية للراصد والمصدر في خط الرؤية. يُحسب المتغير\(v\) على أنه موجب إذا كانت السرعة هي سرعة الركود، وسالبًا إذا كان متغيرًا مقتربًا. نجد حل هذه المعادلة الخاصة بالسرعة
\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]
إذا اقترب نجم منا أو انحسر، فإن الأطوال الموجية للضوء في طيفه المستمر تبدو قصيرة أو مطولة، على التوالي، كما هو الحال بالنسبة للخطوط المظلمة. ومع ذلك، ما لم تكن سرعته عشرات الآلاف من الكيلومترات في الثانية، لا يبدو النجم أكثر زرقة أو احمرارًا بشكل ملحوظ من المعتاد. وبالتالي لا يمكن اكتشاف تحول دوبلر بسهولة في طيف مستمر ولا يمكن قياسه بدقة في مثل هذا الطيف. ومع ذلك، يمكن قياس الأطوال الموجية لخطوط الامتصاص بدقة، ومن السهل نسبيًا اكتشاف تحول دوبلر.
مثال\(\PageIndex{1}\): تأثير دوبلر
يمكننا استخدام معادلة تأثير دوبلر لحساب السرعة الشعاعية لجسم ما إذا كنا نعرف ثلاثة أشياء: سرعة الضوء، والطول الموجي الأصلي (غير المتغير) للضوء المنبعث، والفرق بين الطول الموجي للضوء المنبعث والطول الموجي الذي نلاحظه. بالنسبة لخطوط الامتصاص أو الانبعاث الخاصة، عادة ما نعرف بالضبط الطول الموجي للخط في مختبراتنا على الأرض، حيث لا يتحرك مصدر الضوء. يمكننا قياس الطول الموجي الجديد بأدواتنا في التلسكوب، وهكذا نعرف الفرق في الطول الموجي بسبب تحول دوبلر. نظرًا لأن سرعة الضوء هي ثابت عالمي، يمكننا بعد ذلك حساب السرعة الشعاعية للنجم.
ينبعث خط انبعاث معين من الهيدروجين في الأصل بطول موجة 656.3 nm من سحابة غازية. في التلسكوب الخاص بنا، نلاحظ أن الطول الموجي لخط الانبعاثات هو 656.6 nm. ما مدى سرعة تحرك سحابة الغاز هذه نحو الأرض أو بعيدًا عنها؟
الحل
نظرًا لأن الضوء يتحول إلى طول موجة أطول (يتحول إلى اللون الأحمر)، فإننا نعلم أن سحابة الغاز هذه تبتعد عنا. يمكن حساب السرعة باستخدام صيغة Doppler shift:
\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]
التمارين\(\PageIndex{1}\)
لنفترض أن خطًا طيفيًا من الهيدروجين، عادةً عند 500 نانومتر، لوحظ في طيف النجم عند 500.1 نانومتر. ما مدى سرعة تحرك النجم نحو الأرض أو بعيدًا عنها؟
- إجابة
-
نظرًا لأن الضوء يتحول إلى طول موجة أطول، فإن النجم يتحرك بعيدًا عنا:
\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]
تبلغ سرعته 60،000 متر/ثانية.
قد تسأل الآن: إذا كانت جميع النجوم تتحرك والحركة تغير الطول الموجي لكل خط طيفي، أليس هذا كارثة لعلماء الفلك الذين يحاولون معرفة العناصر الموجودة في النجوم؟ بعد كل شيء، فإن الطول الموجي الدقيق (أو اللون) هو الذي يخبر علماء الفلك عن الخطوط التي تنتمي إلى أي عنصر. ونقوم أولاً بقياس هذه الأطوال الموجية في حاويات الغاز في مختبراتنا، والتي لا تتحرك. إذا كان كل خط في طيف النجم قد تحول الآن بحركته إلى طول موجة مختلف (لون)، فكيف يمكننا التأكد من الخطوط والعناصر التي ننظر إليها في نجم لا نعرف سرعته؟
خذ القلب. يبدو هذا الوضع أسوأ مما هو عليه بالفعل. نادرًا ما يحكم علماء الفلك على وجود عنصر في كائن فلكي بخط واحد. إن نمط الخطوط الفريدة للهيدروجين أو الكالسيوم هو الذي يمكننا من تحديد أن هذه العناصر هي جزء من النجم أو المجرة التي نلاحظها. لا يغير تأثير دوبلر نمط الخطوط من عنصر معين - بل يقوم فقط بتحويل النمط بأكمله قليلاً نحو الأطوال الموجية الأكثر احمرارًا أو زرقة. لا يزال من السهل جدًا التعرف على النمط المتغير. أفضل ما في الأمر أنه عندما نتعرف على نمط عنصر مألوف، نحصل على مكافأة: مقدار تغيير النمط يمكن أن يمكّننا من تحديد سرعة الكائنات في خط رؤيتنا.
يشمل تدريب علماء الفلك الكثير من العمل على تعلم فك شفرة الضوء (والإشعاع الكهرومغناطيسي الآخر). يمكن لـ «وحدة فك التشفير» الماهرة معرفة درجة حرارة النجم، والعناصر الموجودة فيه، وحتى سرعته في اتجاه نحونا أو بعيدًا عنا. هذه حقًا كمية رائعة من المعلومات للنجوم التي تبعد سنوات ضوئية.
ملخص
إذا كانت الذرة تتحرك نحونا عندما يغير الإلكترون مداره وينتج خطًا طيفيًا، فإننا نرى هذا الخط يتحول قليلاً نحو اللون الأزرق لطوله الموجي الطبيعي في الطيف. إذا كانت الذرة تتحرك بعيدًا، فإننا نرى الخط يتحول نحو اللون الأحمر. يُعرف هذا التحول باسم تأثير دوبلر ويمكن استخدامه لقياس السرعات الشعاعية للأجسام البعيدة.
مسرد المصطلحات
- تأثير دوبلر
- التغيير الواضح في الطول الموجي أو تردد الإشعاع من المصدر بسبب حركته النسبية بعيدًا عن أو باتجاه الراصد
- سرعة شعاعية
- الحركة نحو الراصد أو بعيدًا عنه؛ مكون السرعة النسبية الذي يقع في خط الرؤية


