5.1: سلوك الضوء
- Page ID
- 197290
أهداف التعلم
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح الدليل على نموذج ماكسويل الكهرومغناطيسي للضوء
- وصف العلاقة بين الطول الموجي والتردد وسرعة الضوء
- ناقش النموذج الجسيمي للضوء وتعريف الفوتون
- اشرح كيف ولماذا تعتمد كمية الضوء التي نراها من جسم ما على بعده
يتم ترميز مجموعة واسعة من المعلومات في الضوء وأنواع الإشعاع الأخرى التي تصلنا من الأجسام الموجودة في الكون حول شكل هذه الأشياء وكيفية عملها. إذا تمكنا من فك شفرة هذا الرمز وقراءة الرسائل التي يحتوي عليها، فيمكننا معرفة قدر هائل عن الكون دون الحاجة إلى مغادرة الأرض أو بيئتها المباشرة.
يتم إنشاء الضوء المرئي والإشعاع الآخر الذي نتلقاه من النجوم والكواكب من خلال العمليات على المستوى الذري - من خلال التغييرات في طريقة تفاعل أجزاء الذرة وتحريكها. وبالتالي، لتقدير كيفية توليد الضوء، يجب علينا استكشاف كيفية عمل الذرات. هناك القليل من السخرية في حقيقة أنه من أجل فهم بعض أكبر الهياكل في الكون، يجب أن نتعرف على بعض أصغرها.
لاحظ أننا استخدمنا مرتين عبارة «الضوء والإشعاع الآخر». إحدى الأفكار الرئيسية التي تم استكشافها في هذا الفصل هي أن الضوء المرئي ليس فريدًا؛ إنه مجرد المثال الأكثر شيوعًا لعائلة أكبر من الإشعاع يمكنها نقل المعلومات إلينا.
سيتم استخدام كلمة «الإشعاع» بشكل متكرر في هذا الكتاب، لذلك من المهم فهم معناها. في اللغة اليومية، غالبًا ما يستخدم «الإشعاع» لوصف أنواع معينة من الجسيمات دون الذرية النشطة المنبعثة من المواد المشعة في بيئتنا. (مثال على ذلك هو نوع الإشعاع المستخدم لعلاج بعض أنواع السرطان.) لكن هذا ليس ما نعنيه عندما نستخدم كلمة «الإشعاع» في نص علم الفلك. الإشعاع، كما هو مستخدم في هذا الكتاب، هو مصطلح عام للموجات (بما في ذلك موجات الضوء) التي تشع إلى الخارج من المصدر.
كما رأينا في المدارات والجاذبية، تفسر نظرية نيوتن للجاذبية حركات الكواكب وكذلك الأجسام على الأرض. سيطر تطبيق هذه النظرية على مجموعة متنوعة من المشكلات على عمل العلماء لما يقرب من قرنين من الزمان. في القرن التاسع عشر، تحول العديد من علماء الفيزياء إلى دراسة الكهرباء والمغناطيسية، والتي ترتبط ارتباطًا وثيقًا بإنتاج الضوء.
كان العالم الذي لعب دورًا في هذا المجال مشابهًا لدور نيوتن في دراسة الجاذبية هو الفيزيائي جيمس كليرك ماكسويل، الذي ولد وتلقى تعليمه في اسكتلندا (الشكل\(\PageIndex{1}\)). مستوحى من عدد من التجارب المبتكرة التي أظهرت وجود علاقة حميمة بين الكهرباء والمغناطيسية، طور ماكسويل نظرية تصف كلاً من الكهرباء والمغناطيسية بعدد صغير فقط من المعادلات الأنيقة. هذه النظرية هي التي تعطينا رؤى مهمة حول طبيعة وسلوك الضوء.

نظرية ماكسويل للكهرومغناطيسية
سننظر في بنية الذرة بمزيد من التفصيل لاحقًا، لكننا نبدأ بملاحظة أن الذرة النموذجية تتكون من عدة أنواع من الجسيمات، لا يحتوي عدد منها على كتلة فحسب، بل خاصية إضافية تسمى الشحنة الكهربائية. في النواة (الجزء المركزي) من كل ذرة توجد بروتونات ذات شحنة موجبة؛ وخارج النواة توجد إلكترونات لها شحنة سالبة.
تتناول نظرية ماكسويل هذه الشحنات الكهربائية وتأثيراتها، خاصة عندما تتحرك. وفي المنطقة المجاورة لشحنة الإلكترون، تشعر شحنة أخرى بقوة جذب أو تنافر: فالشحنات المتقابلة تتجاذب، كما تتنافر الشحنات. عندما لا تتحرك الشحنات، نلاحظ فقط هذا الجذب الكهربائي أو التنافر. ولكن إذا كانت الشحنات تتحرك (كما هي داخل كل ذرة وفي سلك يحمل تيارًا)، فإننا نقيس قوة أخرى تسمى المغناطيسية.
كانت المغناطيسية معروفة جيدًا بالكثير من التاريخ البشري المسجل، لكن سببها لم يكن مفهومًا حتى القرن التاسع عشر. أظهرت التجارب على الشحنات الكهربائية أن المغناطيسية كانت نتيجة تحريك الجسيمات المشحونة. في بعض الأحيان، تكون الحركة واضحة، كما هو الحال في لفائف الأسلاك الثقيلة التي تصنع مغناطيسًا كهربائيًا صناعيًا. في أحيان أخرى، يكون الأمر أكثر دقة، كما هو الحال في نوع المغناطيس الذي تشتريه من متجر لاجهزة الكمبيوتر، حيث تدور العديد من الإلكترونات داخل الذرات في نفس الاتجاه تقريبًا؛ إن محاذاة حركتها هي التي تجعل المادة تصبح مغناطيسية.
يستخدم الفيزيائيون حقل الكلمة لوصف عمل القوى التي يمارسها كائن ما على الأجسام البعيدة الأخرى. على سبيل المثال، نقول إن الشمس تنتج مجال جاذبية يتحكم في مدار الأرض، على الرغم من عدم ملامسة الشمس والأرض بشكل مباشر. باستخدام هذه المصطلحات، يمكننا القول أن الشحنات الكهربائية الثابتة تنتج مجالات كهربائية، كما تنتج الشحنات الكهربائية المتحركة مجالات مغناطيسية.
في الواقع، العلاقة بين الظواهر الكهربائية والمغناطيسية أكثر عمقًا. أظهرت التجارب أن تغيير المجالات المغناطيسية يمكن أن ينتج تيارات كهربائية (وبالتالي تغيير المجالات الكهربائية)، ويمكن أن يؤدي تغيير التيارات الكهربائية بدوره إلى مجالات مغناطيسية متغيرة. لذلك بمجرد البدء، يمكن أن تستمر تغييرات المجال الكهربائي والمغناطيسي في تحفيز بعضها البعض.
حلل ماكسويل ما سيحدث إذا كانت الشحنات الكهربائية تتأرجح (تتحرك باستمرار ذهابًا وإيابًا) ووجد أن النمط الناتج من المجالات الكهربائية والمغناطيسية سينتشر وينتقل بسرعة عبر الفضاء. يحدث شيء مشابه عندما تضرب قطرة مطر سطح الماء أو يقفز الضفدع إلى البركة. يتحرك الاضطراب إلى الخارج ويخلق نمطًا نسميه موجة في الماء (الشكل\(\PageIndex{2}\)). قد تعتقد، في البداية، أنه يجب أن تكون هناك حالات قليلة جدًا في الطبيعة تتأرجح فيها الشحنات الكهربائية، ولكن هذا ليس هو الحال على الإطلاق. كما سنرى، تتأرجح الذرات والجزيئات (التي تتكون من جزيئات مشحونة) ذهابًا وإيابًا طوال الوقت. تعد الاضطرابات الكهرومغناطيسية الناتجة من أكثر الظواهر شيوعًا في الكون.

كان ماكسويل قادرًا على حساب السرعة التي يتحرك بها الاضطراب الكهرومغناطيسي عبر الفضاء؛ ووجد أنها تساوي سرعة الضوء، والتي تم قياسها تجريبيًا. على هذا الأساس، تكهن بأن الضوء هو أحد أشكال عائلة الاضطرابات الكهرومغناطيسية المحتملة التي تسمى الإشعاع الكهرومغناطيسي، وهو استنتاج تم تأكيده مرة أخرى في التجارب المعملية. عندما يدخل الضوء (المنعكس من صفحات كتاب علم الفلك، على سبيل المثال) إلى عين الإنسان، فإن مجالاته الكهربائية والمغناطيسية المتغيرة تحفز النهايات العصبية، والتي تنقل بعد ذلك المعلومات الواردة في هذه المجالات المتغيرة إلى الدماغ. يدور علم الفلك في المقام الأول حول تحليل الإشعاع من الأجسام البعيدة لفهم ماهيتها وكيفية عملها.
خصائص الضوء الشبيهة بالموجة
تتشابه المجالات الكهربائية والمغناطيسية المتغيرة في الضوء مع الموجات التي يمكن تركيبها في بركة مياه هادئة. في كلتا الحالتين، ينتقل الاضطراب بسرعة إلى الخارج من نقطة المنشأ ويمكن أن يستخدم طاقته لإزعاج أشياء أخرى بعيدة. (على سبيل المثال، في الماء، يمكن للتموجات المتوسعة التي تتحرك بعيدًا عن الضفدع أن تزعج سلام اليعسوب الذي يستريح على ورقة في نفس حوض السباحة.) في حالة الموجات الكهرومغناطيسية، يمكن للإشعاع الناتج عن هوائي الإرسال المليء بالجسيمات المشحونة والإلكترونات المتحركة في محطة الراديو المحلية، في وقت لاحق، أن يزعج مجموعة من الإلكترونات في هوائي راديو سيارتك وينقل لك الأخبار والطقس أثناء القيادة إلى الفصل أو العمل في الصباح.
لكن الموجات الناتجة عن الجسيمات المشحونة تختلف عن موجات الماء في بعض النواحي العميقة. تتطلب موجات الماء الماء لتنتقل إليها. الموجات الصوتية التي نسمعها، على سبيل المثال، هي اضطرابات الضغط التي تتطلب الهواء للتنقل رغم ذلك. لكن الموجات الكهرومغناطيسية لا تتطلب الماء أو الهواء: تولد الحقول بعضها البعض وبالتالي يمكن أن تتحرك عبر الفراغ (مثل الفضاء الخارجي). كانت هذه فكرة مزعجة لعلماء القرن التاسع عشر لدرجة أنهم صنعوا بالفعل مادة لملء كل المساحة - مادة لم يكن هناك دليل واحد عليها - فقط حتى تتمكن موجات الضوء من المرور عبرها: أطلقوا عليها اسم الأثير. نعلم اليوم أنه لا يوجد أثير وأن الموجات الكهرومغناطيسية لا تواجه أي مشكلة على الإطلاق في التحرك عبر الفضاء الفارغ (كما يجب أن تفعل كل النجوم المرئية في ليلة صافية بالتأكيد).
والفرق الآخر هو أن جميع الموجات الكهرومغناطيسية تتحرك بنفس السرعة في الفضاء الفارغ (سرعة الضوء - حوالي 300,000 كيلومتر في الثانية، أو 300,000,000 متر في الثانية، والتي يمكن كتابتها أيضًا بـ 3 × 108 م/ث)، والتي تبين أنها أسرع سرعة ممكنة في الكون. بغض النظر عن المكان الذي تتولد منه الموجات الكهرومغناطيسية وبغض النظر عن الخصائص الأخرى التي تمتلكها، عندما تتحرك (ولا تتفاعل مع المادة)، فإنها تتحرك بسرعة الضوء. ومع ذلك، فأنت تعلم من التجربة اليومية أن هناك أنواعًا مختلفة من الضوء. على سبيل المثال، ندرك أن موجات الضوء تختلف عن بعضها البعض في خاصية نسميها اللون. دعونا نرى كيف يمكننا الإشارة إلى الاختلافات بين عائلة واسعة من الموجات الكهرومغناطيسية.
الشيء الجميل في الموجة هو أنها ظاهرة متكررة. سواء كانت الحركة صعودًا وهبوطًا لموجة مائية أو المجالات الكهربائية والمغناطيسية المتغيرة في موجة الضوء، فإن نمط الاضطراب يتكرر بطريقة دورية. وبالتالي، يمكن وصف أي حركة موجية بسلسلة من القمم والأحواض (الشكل\(\PageIndex{3}\)). الانتقال من قمة واحدة عبر حوض إلى القمة التالية يكمل دورة واحدة. الطول الأفقي الذي تغطيه دورة واحدة يسمى الطول الموجي. توفر موجات المحيط تشبيهًا: الطول الموجي هو المسافة التي تفصل بين قمم الموجات المتتالية.
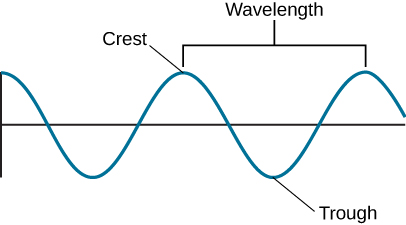
بالنسبة للضوء المرئي، ترى أعيننا أطوال موجية مختلفة كألوان مختلفة: الأحمر، على سبيل المثال، هو أطول طول موجي مرئي، والبنفسجي هو الأقصر. يمكن تذكر الألوان الرئيسية للضوء المرئي من الطول الموجي الأطول إلى الأقصر باستخدام الذاكرة ROY G Biv - للأحمر R، والبرتقالي O، والأصفر Y، والأخضر G، والأزرق B، والنيلي I، والبنفسجي. الأشكال الأخرى غير المرئية للإشعاع الكهرومغناطيسي لها أطوال موجية مختلفة، كما سنرى في القسم التالي.
يمكننا أيضًا تمييز الموجات المختلفة من خلال ترددها، وهو عدد دورات الموجة التي تمر في الثانية. إذا قمت بحساب 10 قمم تتحرك كل ثانية، على سبيل المثال، فإن التردد هو 10 دورات في الثانية (cps). تكريمًا لهاينريش هيرتز، الفيزيائي الذي اكتشف موجات الراديو، المستوحى من عمل ماكسويل، يُطلق على cps أيضًا اسم هيرتز (Hz). ألقِ نظرة على الراديو الخاص بك، على سبيل المثال، وسترى القناة المخصصة لكل محطة راديو تتميز بترددها، عادةً بوحدات كيلوهرتز (كيلوهرتز، أو آلاف الهيرتز) أو ميجاهرتز (ميغا هرتز، أو ملايين الهيرتز).
يرتبط الطول الموجي (\(\lambda\)\(f\)) والتردد () لأن جميع الموجات الكهرومغناطيسية تنتقل بنفس السرعة. لمعرفة كيفية عمل ذلك، تخيل عرضًا يضطر فيه الجميع بسبب ظروف حركة المرور السائدة إلى التحرك بنفس السرعة تمامًا. أنت تقف على زاوية وتشاهد موجات المتظاهرين وهي تأتي. ترى أولاً صفًا تلو الآخر من المهور المصغرة. نظرًا لأنها ليست كبيرة جدًا وبالتالي لها طول موجي أقصر، يمكن لعدد كبير من المهور أن يتجاوزك كل دقيقة؛ يمكننا القول أن لها ترددًا عاليًا. لكن بعد ذلك تأتي عدة صفوف من أفيال السيرك. الفيلة كبيرة الحجم وتسير بنفس سرعة المهور، لذا فإن عددًا أقل بكثير منها يمكنه تجاوزك في الدقيقة: نظرًا لامتلاكها مسافات أوسع (طول موجي أطول)، فإنها تمثل ترددًا أقل.
يمكن التعبير عن صيغة هذه العلاقة على النحو التالي: بالنسبة لأي حركة موجية، فإن السرعة التي تتحرك بها الموجة تساوي التردد مضروبًا في الطول الموجي. الموجات ذات الأطوال الموجية الأطول لها ترددات أقل. رياضياً، يمكننا التعبير عن هذا كـ
\[c=λf \nonumber\]
حيث يُستخدم الحرف اليوناني لـ «l»\(\lambda\) —lambda، للدلالة على الطول الموجي وc هو الرمز العلمي لسرعة الضوء. عند حل الطول الموجي، يتم التعبير عن ذلك على النحو التالي:
\[λ=cf. \nonumber\]
مثال\(\PageIndex{1}\): اشتقاق معادلة الموجة واستخدامها
يمكن اشتقاق معادلة العلاقة بين السرعة والخصائص الأخرى للموجة من فهمنا الأساسي للحركة. متوسط سرعة أي شيء يتحرك هو:
\[\text{average speed}= \text{distance} \times \text{time} \nonumber\]
(لذلك، على سبيل المثال، تغطي سيارة على الطريق السريع تسير بسرعة 100 كم/ساعة 100 كيلومتر خلال فترة ساعة واحدة.) لكي تقطع الموجة الكهرومغناطيسية مسافة أحد أطوال\(\lambda\) موجاتها، بسرعة الضوء\(c\)، لدينا\(c = \lambda /t\). تردد الموجة هو عدد الدورات في الثانية. إذا كان تردد الموجة مليون دورة في الثانية، فإن الوقت الذي تمر فيه كل دورة هو جزء من مليون من الثانية. لذلك، بشكل عام،\(t = 1/f\). وبالاستبدال في معادلة الموجة الخاصة بنا، نحصل على\(c = \lambda \times f\). الآن دعونا نستخدم هذا لحساب مثال. ما الطول الموجي للضوء المرئي الذي تردده 5.66 × 1014 Hz؟
الحل
عند حل معادلة الموجة للطول الموجي، نجد:
\[λ=cf \nonumber\]
استبدال قيمنا يعطي:
\[λ=3.00×10^8\, \text{ m/s} = 5.66×10^{14} \text{ Hz}=5.30×10^{–7}\, \text{ m} \nonumber\]
يمكن أيضًا كتابة هذه الإجابة على النحو 530 نانومتر، وهو في الجزء الأصفر-الأخضر من الطيف المرئي (nm تعني النانومترات، حيث يعني مصطلح «nano» «المليارات»).
التمارين\(\PageIndex{1}\)
«موجات المد والجزر»، أو التسونامي، هي موجات تسببها الزلازل التي تنتقل بسرعة عبر المحيط. إذا انتقل تسونامي بسرعة 600 كم/ساعة واقترب من الشاطئ بمعدل قمة موجة واحدة كل 15 دقيقة (4 موجة/ساعة)، فما هي المسافة بين قمم الأمواج في البحر؟
- إجابة
-
\[ \lambda = \frac{600 \text{ km/h}}{4 \text{ waves/h}} =150 \text{ km} \nonumber\]
ضوء كفوتون
كان نموذج الموجة الكهرومغناطيسية للضوء (كما صاغه ماكسويل) أحد الانتصارات العظيمة لعلوم القرن التاسع عشر. في عام 1887، عندما صنع هاينريش هيرتز فعليًا موجات كهرومغناطيسية غير مرئية (ما يسمى اليوم موجات الراديو) على جانب واحد من الغرفة واكتشفها على الجانب الآخر، كان ذلك إيذانًا بعصر جديد أدى إلى العصر الحديث للاتصالات. أدت تجربته في النهاية إلى تقنيات التلفزيون والهواتف المحمولة والشبكات اللاسلكية الحالية في جميع أنحاء العالم.
ومع ذلك، بحلول بداية القرن العشرين، كشفت تجارب أكثر تعقيدًا أن الضوء يتصرف بطرق معينة لا يمكن تفسيرها بنموذج الموجة. على مضض، كان على علماء الفيزياء أن يتقبلوا أن الضوء يتصرف أحيانًا مثل «الجسيم» - أو على الأقل حزمة طاقة قائمة بذاتها - أكثر من الموجة. نسمي هذه الحزمة من الطاقة الكهرومغناطيسية بالفوتون.
كانت حقيقة أن الضوء يتصرف كموجة في تجارب معينة ومثل جسيم في تجارب أخرى فكرة مفاجئة للغاية وغير محتملة. بعد كل شيء، يقول الفطرة السليمة لدينا أن الموجات والجسيمات هي مفاهيم معاكسة. من ناحية، تعتبر الموجة اضطرابًا متكررًا لا يوجد بطبيعته في مكان واحد فقط، ولكنه ينتشر. الجسيم، من ناحية أخرى، هو شيء يمكن أن يكون في مكان واحد فقط في أي وقت. على الرغم من غرابة الأمر، فإن التجارب التي لا تعد ولا تحصى تؤكد الآن أن الإشعاع الكهرومغناطيسي يمكن أن يتصرف أحيانًا مثل الموجة وفي أوقات أخرى مثل الجسيمات.
ثم مرة أخرى، ربما لا ينبغي أن نتفاجأ من أن شيئًا ما ينتقل دائمًا عند «الحد الأقصى لسرعة» الكون ولا يحتاج إلى وسيط للتنقل عبره قد لا يخضع لأفكارنا المنطقية اليومية. تم حل الارتباك الذي تسببت فيه ثنائية الموجة والجسيمات للضوء في الفيزياء في نهاية المطاف من خلال إدخال نظرية أكثر تعقيدًا للموجات والجسيمات، تسمى الآن ميكانيكا الكم. (هذا هو أحد أكثر مجالات العلوم الحديثة إثارة للاهتمام، ولكنه في الغالب خارج نطاق كتابنا. إذا كنت مهتمًا بها، فراجع بعض الموارد المقترحة في نهاية هذا الفصل.)
على أي حال، يجب أن تكون مستعدًا الآن عندما يناقش العلماء (أو مؤلفو هذا الكتاب) أحيانًا الإشعاع الكهرومغناطيسي كما لو كان يتكون من موجات وفي أوقات أخرى يشيرون إليه على أنه تيار من الفوتونات. يحمل الفوتون (حزمة طاقة) كمية محددة من الطاقة. يمكننا استخدام فكرة الطاقة لتوصيل نماذج الفوتون والموجة. يعتمد مقدار الطاقة التي يمتلكها الفوتون على تردده عندما تفكر فيه كموجة. تحتوي الموجة الراديوية منخفضة الطاقة على تردد منخفض كموجة، في حين أن الأشعة السينية عالية الطاقة في عيادة طبيب الأسنان هي موجة عالية التردد. من بين ألوان الضوء المرئي، تتمتع فوتونات الضوء البنفسجي بأعلى طاقة، بينما تتمتع فوتونات الضوء الأحمر بأدنى مستوى.
اختبر ما إذا كان الاتصال بين الفوتونات والموجات واضحًا لك. في المثال أعلاه، ما الفوتون الذي سيكون له الطول الموجي الأطول كموجة: الموجة الراديوية أم الأشعة السينية؟ إذا أجبت على موجة الراديو، فأنت على صواب. تحتوي موجات الراديو على تردد أقل، وبالتالي فإن دورات الموجة أطول (فهي أفيال وليست مهور مصغرة).
انتشار الضوء
دعونا نفكر للحظة في كيفية انتقال الضوء من المصباح الكهربائي عبر الفضاء. مع تمدد الأمواج، تنتقل بعيدًا عن المصباح، ليس فقط نحو عينيك ولكن في جميع الاتجاهات. لذلك يجب أن تغطي مساحة متزايدة الاتساع. ومع ذلك، لا يمكن تغيير إجمالي كمية الضوء المتاحة بمجرد مغادرة الضوء للمصباح. وهذا يعني أنه نظرًا لأن نفس غلاف الضوء المتوسع يغطي مساحة أكبر وأكبر، يجب أن يكون هناك القليل منه في أي مكان معين. يصبح الضوء (وجميع الإشعاعات الكهرومغناطيسية الأخرى) أضعف وأضعف كلما ابتعد عن مصدره.
تتناسب الزيادة في المساحة التي يجب أن يغطيها الضوء مع مربع المسافة التي قطعها الضوء (الشكل\(\PageIndex{4}\)). إذا وقفنا بعيدًا مرتين عن المصدر، فستواجه أعيننا ضوءًا مربعًا (2 × 2)، أو أقل بأربع مرات من الضوء. إذا وقفنا بعيدًا عن المصدر بعشر مرات، نحصل على إضاءة مربعة بمقدار 10 أضعاف، أو أقل بـ 100 مرة. يمكنك أن ترى كيف يعني هذا الضعف مشكلة لمصادر الضوء على مسافات فلكية. واحدة من أقرب النجوم، Alpha Centauri A، تنبعث منها نفس الطاقة الكلية للشمس. لكنها أبعد بحوالي 270,000 مرة، وبالتالي يبدو أنها أضعف بحوالي 73 مليار مرة. لا عجب في أن النجوم، التي ستبدو عن قرب تشبه الشمس إلى حد ما، تبدو وكأنها نقاط ضوئية خافتة من بعيد.
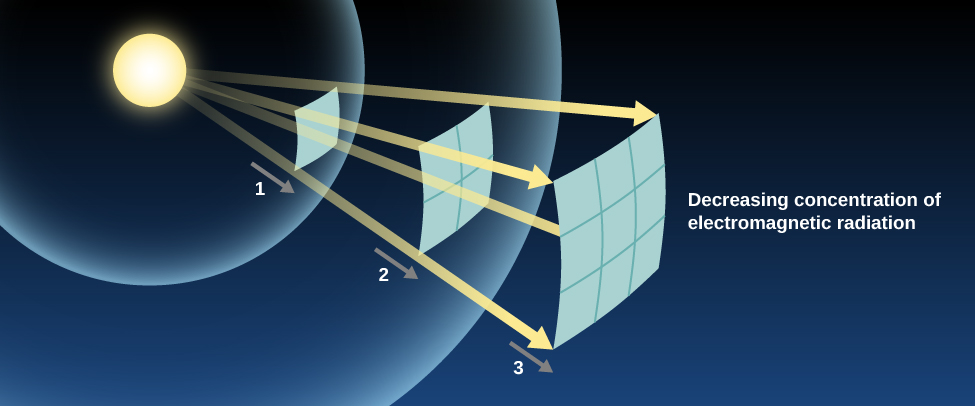
تُعرف هذه الفكرة - وهي أن السطوع الظاهري للمصدر (مدى سطوعه بالنسبة لنا) يزداد ضعفًا مع المسافة بالطريقة التي وصفناها - باسم قانون المربع العكسي لانتشار الضوء. في هذا الصدد، يشبه انتشار الضوء تأثيرات الجاذبية. تذكر أن قوة الجاذبية بين كتلتين جاذبيتين تتناسب أيضًا عكسيًا مع مربع الفصل بينهما.
مثال\(\PageIndex{2}\): قانون المربع العكسي للضوء
تبلغ شدة المصباح 120 واط الذي تمت ملاحظته من مسافة 2 متر 2.4 واط/م 2. ماذا ستكون الكثافة إذا تضاعفت هذه المسافة؟
الحل
إذا ابتعدنا بمقدار الضعف، فستتغير الإجابة وفقًا للمربع العكسي للمسافة، وبالتالي ستكون\((1/2)^2 = 1/4\) الكثافة الجديدة بالكثافة الأصلية، أو 0.6 واط/م 2.
التمارين\(\PageIndex{2}\)
كم مرة سيظهر النجم أكثر سطوعًا أو خافتًا إذا تم نقله إلى:
- ضعف المسافة الحالية؟
- عشرة أضعاف المسافة الحالية؟
- نصف المسافة الحالية؟
- إجابة
-
\[\text{a. } \left( \frac{1}{2} \right)^2= \frac{1}{4}; ~ \text{b. } \left( \frac{1}{10} \right)^2= \frac{1}{100} \left( \frac{1}{10} \right)^2= \frac{1}{100}; ~ \text{c. } \left( \frac{1}{1/2} \right)^2= 4 \nonumber\]
المفاهيم الأساسية والملخص
أظهر جيمس كليرك ماكسويل أنه عندما تغير الجسيمات المشحونة حركتها، كما يحدث في كل ذرة وجزيء، فإنها تطلق موجات من الطاقة. الضوء هو أحد أشكال هذا الإشعاع الكهرومغناطيسي. يحدد الطول الموجي للضوء لون الإشعاع المرئي. يرتبط الطول الموجي (\(\lambda\)) بالتردد (\(f\)) وسرعة الضوء (\(c\)) بالمعادلة\(c = \lambda f\). يتصرف الإشعاع الكهرومغناطيسي أحيانًا مثل الموجات، ولكن في أوقات أخرى، يتصرف كما لو كان جسيمًا - حزمة صغيرة من الطاقة تسمى الفوتون. يتناقص السطوع الظاهري لمصدر الطاقة الكهرومغناطيسية مع زيادة المسافة من هذا المصدر بما يتناسب مع مربع المسافة - وهي علاقة تعرف باسم قانون المربع العكسي.
مسرد المصطلحات
- إشعاع كهرومغناطيسي
- يتكون الإشعاع من موجات تنتشر عبر مجالات كهربائية ومغناطيسية متغيرة بانتظام وتتحرك بسرعة الضوء
- التردد
- عدد الموجات التي تعبر نقطة معينة لكل وحدة زمنية (في الإشعاع)
- قانون التربيع العكسي
- (للضوء) تقل كمية الطاقة (الضوء) المتدفقة عبر منطقة معينة في وقت معين بما يتناسب مع مربع المسافة من مصدر الطاقة أو الضوء
- فوتون
- وحدة منفصلة (أو «حزمة») من الطاقة الكهرومغناطيسية
- الطول الموجي
- المسافة من القمة إلى القمة أو من الحوض إلى الحوض الصغير في الموجة


