3.1: قوانين حركة الكواكب

أهداف التعلم

في نهاية القسم، ستكون قادرًا على:

• وصف كيف ساهم تايكو براهي ويوهانس كيبلر في فهمنا لكيفية تحرك الكواكب حول الشمس
• شرح قوانين كيبلر الثلاثة لحركة الكواكب

في الوقت الذي بدأ فيه غاليليو تجاربه مع الأجسام الساقطة، أدت جهود عالمين آخرين إلى تعزيز فهمنا لحركات الكواكب بشكل كبير. كان هذان الفلكيون هما المراقب تايكو براهي وعالم الرياضيات يوهانس كيبلر. لقد وضعوا معًا تكهنات كوبرنيكوس على أساس رياضي سليم ومهدوا الطريق لعمل إسحاق نيوتن في القرن التالي.

مرصد تايكو براهي

بعد ثلاث سنوات من نشر كتاب كوبرنيكوس De Revolutionibus، وُلد تايكو براهي لعائلة من طبقة النبلاء الدنماركية. لقد طور اهتمامًا مبكرًا بعلم الفلك، وعندما كان شابًا، قدم ملاحظات فلكية مهمة. كان من بين هذه الدراسات دراسة متأنية لما نعرفه الآن عن نجم متفجر اشتعل لتألق كبير في سماء الليل. أكسبته شهرته المتنامية رعاية الملك الدنماركي فريدريك الثاني، وفي سن الثلاثين، تمكن براهي من إنشاء مرصد فلكي جيد في جزيرة هفين في بحر الشمال (الشكل$\PageIndex{1}$). كان Brahe آخر وأعظم المراقبين قبل التلسكوبيين في أوروبا.

الشكل$\PageIndex{1}$: تايكو براهي (1546-1601) ويوهانس كيبلر (1571-1630). (أ) يُظهر نقش منمق تايكو براهي وهو يستخدم أدواته لقياس ارتفاع الأجرام السماوية فوق الأفق. سمحت له الأداة المنحنية الكبيرة في المقدمة بقياس الزوايا الدقيقة في السماء. لاحظ أن المشهد يتضمن تلميحات عن عظمة مرصد Brahe في Hven. (ب) كان كيبلر عالم رياضيات وفلك ألماني. أدى اكتشافه للقوانين الأساسية التي تصف حركة الكواكب إلى وضع علم الكونيات الشمسي لكوبرنيكوس على أساس رياضي ثابت.

في Hven، سجل Brahe سجلاً مستمرًا لمواقع الشمس والقمر والكواكب لمدة 20 عامًا تقريبًا. مكنته ملاحظاته الواسعة والدقيقة من ملاحظة أن مواقع الكواكب تختلف عن تلك الواردة في الجداول المنشورة، والتي استندت إلى عمل بطليموس. كانت هذه البيانات ذات قيمة كبيرة، ولكن لم يكن لدى براهي القدرة على تحليلها وتطوير نموذج أفضل مما نشره بطليموس. تم منعه أكثر من ذلك لأنه كان زميلًا فخمًا وشديدًا، وتراكمت لديه أعداء بين المسؤولين الحكوميين. عندما توفي راعيه فريدريك الثاني عام 1597، فقد براهي قاعدته السياسية وقرر مغادرة الدنمارك. استقر في براغ، حيث أصبح عالم فلك البلاط للإمبراطور رودولف من بوهيميا. هناك، في السنة التي سبقت وفاته، وجد براهي عالم الرياضيات الشاب الأكثر قدرة، يوهانس كيبلر، لمساعدته في تحليل بياناته الكوكبية الواسعة.

يوهانس كيبلر

ولد يوهانس كيبلر لعائلة فقيرة في مقاطعة فورتمبيرغ الألمانية وعاش معظم حياته وسط اضطرابات حرب الثلاثين عامًا (انظر الشكل$\PageIndex{1}$). التحق بالجامعة في توبنغن ودرس في مهنة لاهوتية. هناك، تعلم مبادئ نظام كوبرنيكان وتحول إلى فرضية مركزية الشمس. في النهاية، ذهب كيبلر إلى براغ للعمل كمساعد لبراهي، الذي جعله يعمل محاولًا إيجاد نظرية مرضية لحركة الكواكب - نظرية متوافقة مع السلسلة الطويلة من الملاحظات التي تمت في Hven. كان براهي مترددًا في تزويد كيبلر بالكثير من المواد في أي وقت خوفًا من أن يكتشف كيبلر أسرار الحركة العالمية بنفسه، وبالتالي يسلب براهي بعضًا من المجد. فقط بعد وفاة براهي في عام 1601، حصل كيبلر على حيازة كاملة للسجلات التي لا تقدر بثمن. استغرقت دراستهم معظم وقت كيبلر لأكثر من 20 عامًا.

من خلال تحليله لحركات الكواكب، طور كيبلر سلسلة من المبادئ، المعروفة الآن باسم قوانين كيبلر الثلاثة، والتي تصف سلوك الكواكب بناءً على مساراتها عبر الفضاء. تم نشر أول قانونين لحركة الكواكب في عام 1609 في The New Astronomy. كان اكتشافهم خطوة عميقة في تطوير العلوم الحديثة.

أول قانونين لحركة الكواكب

يُطلق على مسار الجسم عبر الفضاء اسم مداره. افترض كيبلر في البداية أن مدارات الكواكب عبارة عن دوائر، لكن القيام بذلك لم يسمح له بالعثور على مدارات تتفق مع ملاحظات براهي. وبالعمل مع البيانات الخاصة بالمريخ، اكتشف في النهاية أن مدار هذا الكوكب له شكل دائرة مسطحة إلى حد ما، أو شكل بيضاوي. بجانب الدائرة، يعتبر الشكل البيضاوي أبسط أنواع المنحنيات المغلقة، وينتمي إلى عائلة من المنحنيات تعرف باسم المقاطع المخروطية (الشكل$\PageIndex{2}$).

الشكل: المقاطع$\PageIndex{2}$ المخروطية. تتكون كل من الدائرة والقطع الناقص والقطع المكافئ والمفرط من خلال تقاطع مستوى مع مخروط. هذا هو السبب في أن هذه المنحنيات تسمى الأقسام المخروطية.

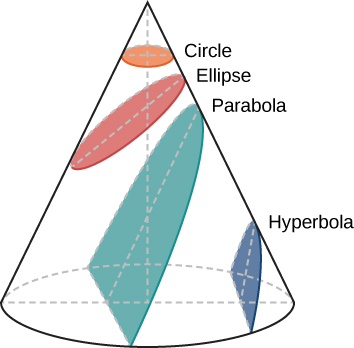
قد تتذكر من دروس الرياضيات أن المركز يمثل نقطة خاصة في الدائرة. المسافة من المركز إلى أي مكان في الدائرة هي نفسها تمامًا. في الشكل البيضاوي، يكون مجموع المسافة من نقطتين خاصتين داخل الشكل البيضاوي إلى أي نقطة على الشكل البيضاوي هو نفسه دائمًا. تسمى هاتان النقطتان داخل الشكل البيضاوي بؤره (المفرد: التركيز)، وهي كلمة اخترعها كيبلر لهذا الغرض.

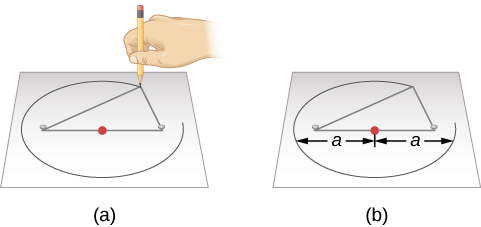
تقترح هذه الخاصية طريقة بسيطة لرسم شكل بيضاوي (الشكل$\PageIndex{3}$). نلف طرفي حلقة من الخيط حول مسندين يتم دفعهما عبر ورقة إلى لوحة رسم، بحيث تكون السلسلة متراخية. إذا ضغطنا قلم رصاص على الخيط، مما جعل الخيط مشدودًا، ثم حرّكنا القلم الرصاص على الخيط في جميع أنحاء المسامير، فإن المنحنى الناتج هو شكل بيضاوي. في أي نقطة يكون فيها القلم الرصاص، يكون مجموع المسافات من القلم الرصاص إلى المسندين طولًا ثابتًا - طول الخيط. تقع المسامير في بؤري الشكل البيضاوي.

يُطلق على أكبر قطر للقطع الناقص محوره الرئيسي. نصف هذه المسافة - أي المسافة من مركز القطع الناقص إلى أحد طرفيه - هي المحور شبه الرئيسي، والذي يُستخدم عادةً لتحديد حجم القطع الناقص. على سبيل المثال، يبلغ المحور شبه الرئيسي لمدار المريخ، وهو أيضًا متوسط مسافة الكوكب من الشمس، 228 مليون كيلومتر.

الشكل:$\PageIndex{3}$ رسم القطع الناقص. (أ) يمكننا إنشاء شكل بيضاوي عن طريق دفع مسندين (الأجسام البيضاء) إلى قطعة من الورق على لوحة رسم، ثم تحريك خيط حول المسامير. يمثل كل مسار محور الشكل البيضاوي، وأحد المسامير هو الشمس. قم بتمديد الخيط بإحكام باستخدام قلم رصاص، ثم حرك القلم الرصاص حول المسامير. يظل طول السلسلة كما هو، بحيث يكون مجموع المسافات من أي نقطة على الشكل البيضاوي إلى البؤر ثابتًا دائمًا. (ب) في هذا الرسم التوضيحي، يُشار إلى كل محور شبه رئيسي بـ a. وتُسمى المسافة 2a بالمحور الرئيسي للقطع الناقص.

يعتمد شكل (استدارة) الشكل البيضاوي على مدى قرب البؤرتين، مقارنة بالمحور الرئيسي. وتسمى نسبة المسافة بين البؤر إلى طول المحور شبه الرئيسي بانحراف الشكل البيضاوي.

إذا تم نقل البؤر (أو المسامير) إلى نفس الموقع، فستكون المسافة بين البؤر صفرًا. هذا يعني أن الانحراف المركزي هو صفر والقطع الناقص هو مجرد دائرة؛ وبالتالي، يمكن تسمية الدائرة بقطع بيضاوي من الانحراف الصفري. في الدائرة، سيكون المحور شبه الرئيسي هو نصف القطر.

بعد ذلك، يمكننا عمل أشكال بيضاوية ذات استطالات مختلفة (أو أطوال ممتدة) عن طريق تغيير تباعد المسامير (طالما أنها ليست بعيدة عن طول السلسلة). كلما زاد الانحراف، زاد طول الشكل البيضاوي، حتى أقصى انحراف مركزي يبلغ 1.0، عندما يصبح القطع الناقص «مسطحًا»، بينما يكون الطرف الآخر متطرفًا من الدائرة.

يتم تحديد حجم وشكل القطع الناقص تمامًا من خلال محوره شبه الرئيسي وانحرافه. باستخدام بيانات براهي، وجد كيبلر أن المريخ له مدار بيضاوي، مع تركيز الشمس على تركيز واحد (التركيز الآخر فارغ). يبلغ الانحراف المركزي لمدار المريخ حوالي 0.1 فقط؛ مداره، المرسوم على نطاق واسع، لن يكون من الممكن تمييزه عمليًا عن الدائرة، ولكن تبين أن الاختلاف أمر بالغ الأهمية لفهم حركات الكواكب.

عمم كيبلر هذه النتيجة في قانونه الأول وقال إن مدارات جميع الكواكب عبارة عن أشكال بيضاوية. كانت هذه لحظة حاسمة في تاريخ الفكر الإنساني: لم يكن من الضروري وجود دوائر فقط من أجل الحصول على كون مقبول. يمكن أن يكون الكون أكثر تعقيدًا قليلاً مما أراده الفلاسفة اليونانيون.

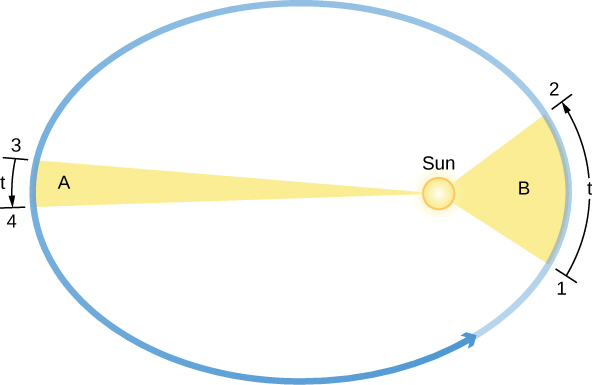
يتناول قانون كيبلر الثاني السرعة التي يتحرك بها كل كوكب على طول شكله البيضاوي، والمعروف أيضًا باسم سرعته المدارية. من خلال العمل على ملاحظات براهي للمريخ، اكتشف كيبلر أن الكوكب يتسارع مع اقترابه من الشمس ويتباطأ مع ابتعاده عن الشمس. عبّر عن الشكل الدقيق لهذه العلاقة من خلال تخيل أن الشمس والمريخ متصلتان بخط مستقيم ومرن. عندما يكون المريخ أقرب إلى الشمس (الموقعان 1 و 2 في الشكل$\PageIndex{4}$)، لا يمتد الخط المرن كثيرًا، ويتحرك الكوكب بسرعة. بعيدًا عن الشمس، كما هو الحال في المواضع 3 و 4، يمتد الخط كثيرًا، ولا يتحرك الكوكب بسرعة كبيرة. أثناء انتقال المريخ في مداره الإهليلجي حول الشمس، يكتسح الخط المرن مناطق الشكل البيضاوي أثناء تحركه (المناطق الملونة في الشكل الخاص بنا). وجد كيبلر أنه في فترات متساوية من الوقت (t)، تكون المساحات التي تم اجتياحها في الفضاء بواسطة هذا الخط التخيلي متساوية دائمًا؛ أي أن مساحة المنطقة B من 1 إلى 2 هي نفس مساحة المنطقة A من 3 إلى 4.

إذا تحرك كوكب في مدار دائري، فإن الخط المرن يمتد دائمًا بنفس المقدار ويتحرك الكوكب بسرعة ثابتة حول مداره. ولكن، كما اكتشف كيبلر، في معظم المدارات، تميل سرعة الكوكب الذي يدور حول نجمه (أو القمر الذي يدور حول كوكبه) إلى التباين لأن المدار بيضاوي الشكل.

الشكل: قانون$\PageIndex{4}$ كيبلر الثاني: قانون المناطق المتساوية. تختلف السرعة المدارية لكوكب يسافر حول الشمس (الجسم الدائري داخل الشكل البيضاوي) بطريقة تجعل الخط الفاصل بين الشمس والكوكب يجتاح مناطق متساوية (A و B) في فترات زمنية متساوية (t). لاحظ أن الانحرافات في مدارات الكواكب في مجموعتنا الشمسية أقل بكثير مما هو موضح هنا.

قانون كبلر الثالث

يصف أول قانونين لحركة الكواكب في كيبلر شكل مدار الكوكب ويسمحون لنا بحساب سرعة حركته في أي نقطة في المدار. كان كيبلر سعيدًا باكتشاف مثل هذه القواعد الأساسية، لكنها لم ترضي سعيه لفهم حركات الكواكب بشكل كامل. أراد أن يعرف سبب تباعد مدارات الكواكب كما هي وإيجاد نمط رياضي في حركاتها - «تناغم الكرات» كما سماها. عمل لسنوات عديدة على اكتشاف العلاقات الرياضية التي تحكم تباعد الكواكب والوقت الذي يستغرقه كل كوكب للالتفاف حول الشمس.

في عام 1619، اكتشف كيبلر علاقة أساسية لربط مدارات الكواكب بمسافاتها النسبية من الشمس. نحن نحدد الفترة المدارية للكوكب، ($P$)، على أنها الوقت الذي يستغرقه الكوكب للسفر مرة واحدة حول الشمس. تذكر أيضًا أن المحور شبه الرئيسي للكوكب، a، يساوي متوسط المسافة من الشمس. تشير العلاقة، المعروفة الآن باسم قانون كيبلر الثالث، إلى أن الفترة المدارية المربعة للكوكب تتناسب مع المحور شبه الرئيسي لمداره المكعب، أو

$$P^2 \propto a^3 \nonumber$$

عندما يتم قياس$P$ (الفترة المدارية) بالسنوات، ويتم التعبير عن a بكمية تعرف باسم الوحدة الفلكية (AU)، فإن جانبي الصيغة لا يكونان متناسبين فحسب، بل متساويين أيضًا. واحد AU هو متوسط المسافة بين الأرض والشمس ويساوي تقريبًا 1.5 × 108 كيلومترًا. في هذه الوحدات،

$$P^2=a^3 \nonumber$$

ينطبق قانون كيبلر الثالث على جميع الأجسام التي تدور حول الشمس، بما في ذلك الأرض، ويوفر وسيلة لحساب المسافات النسبية بينها وبين الشمس من الوقت الذي تستغرقه في المدار. دعونا ننظر إلى مثال محدد لتوضيح مدى فائدة قانون كبلر الثالث.

على سبيل المثال، لنفترض أنك تستغرق الوقت الذي يستغرقه المريخ للالتفاف حول الشمس (في سنوات الأرض). يمكن بعد ذلك استخدام قانون كبلر الثالث لحساب متوسط مسافة المريخ من الشمس. الفترة المدارية للمريخ (1.88 سنة أرضية) مربعة$P^2$، أو هي 1.882 = 3.53، ووفقًا لمعادلة قانون كيبلر الثالث، فإن هذا يساوي مكعب محوره شبه الرئيسي، أو$a^3$. إذن ما العدد الذي يجب تكبيره لإعطاء 3.53؟ الجواب هو 1.52 (منذ$1.52 \times 1.52 \times 1.52 = 3.53$). وبالتالي، يجب أن يكون محور المريخ شبه الرئيسي في الوحدات الفلكية هو 1.52 AU. بعبارة أخرى، للالتفاف حول الشمس في أقل من عامين بقليل، يجب أن يكون المريخ بعيدًا عن الشمس مثل الأرض بحوالي 50٪ (النصف مرة أخرى).

مثال$\PageIndex{1}$: حساب الفترات

تخيل أن شيئًا ما يسافر حول الشمس. ماذا ستكون الفترة المدارية للجسم إذا كان مداره يحتوي على محور شبه رئيسي قدره 50 AU؟

الحل

من قانون كيبلر الثالث، نعلم ذلك (عندما نستخدم وحدات السنوات والاتحاد الأفريقي)

$$P^2=a^3 \nonumber$$

إذا كان مدار الجسم يحتوي على محور شبه رئيسي قدره 4 AU (a = 50)، فيمكننا تكعيب 50 ثم أخذ الجذر التربيعي للنتيجة للحصول على P:

$$\begin{array}{l} P = \sqrt{a^3} \\ P = \sqrt{50 \times 50 \times 50} = \sqrt{125,000} = 353.6 \text{ years} \end{array}$$

لذلك، تبلغ الفترة المدارية للجسم حوالي 350 عامًا. هذا من شأنه أن يضع كائننا الافتراضي خارج مدار بلوتو.

التمارين$\PageIndex{1}$

ماذا ستكون الفترة المدارية لكويكب (قطعة صخرية بين المريخ والمشتري) بمحور شبه رئيسي قدره 3 AU؟

إجابة

$$P = \sqrt{3 \times 3 \times 3} = \sqrt{27} = 5.2 \text{ years}$$

يمكن تلخيص قوانين كبلر الثلاثة لحركة الكواكب على النحو التالي:

• قانون كيبلر الأول: يتحرك كل كوكب حول الشمس في مدار بيضاوي، مع تركيز الشمس في أحد محاور الشكل البيضاوي.
• قانون كبلر الثاني: الخط المستقيم الذي يربط الكوكب والشمس يجتاح مناطق متساوية في الفضاء على فترات زمنية متساوية.
• قانون كبلر الثالث: يتناسب مربع الفترة المدارية للكوكب بشكل مباشر مع مكعب المحور شبه الرئيسي لمداره.

توفر قوانين كيبلر الثلاثة وصفًا هندسيًا دقيقًا لحركة الكواكب في إطار نظام كوبرنيكان. باستخدام هذه الأدوات، كان من الممكن حساب مواقع الكواكب بدقة محسنة بشكل كبير. ومع ذلك، فإن قوانين كيبلر وصفية بحتة: فهي لا تساعدنا على فهم قوى الطبيعة التي تقيد الكواكب لاتباع هذه المجموعة المحددة من القواعد. تم ترك هذه الخطوة لإسحاق نيوتن.

مثال$\PageIndex{2}$: تطبيق قانون كبلر الثالث

باستخدام الفترات المدارية والمحاور شبه الرئيسية لكوكب الزهرة والأرض المتوفرة هنا، احسب$P^2$ وتحقق$a^3$ من أنها تخضع لقانون كيبلر الثالث. الفترة المدارية لكوكب الزهرة هي 0.62 سنة، ومحورها شبه الرئيسي هو 0.72 AU. الفترة المدارية للأرض هي 1.00 عام، ومحورها شبه الرئيسي هو 1.00 AU.

الحل

يمكننا استخدام معادلة قانون كيبلر الثالث,$P^2 \propto a^3$. بالنسبة لكوكب الزهرة،$P^2 = 0.62 \times 0.62 = 0.38 \text{ years}$ و$a^3 = 0.72 \times 0.72 \times 0.72 = 0.37 \text{ AU}$ (يؤدي تقريب الأرقام أحيانًا إلى اختلافات طفيفة مثل هذه). تقترب الفترة المدارية (0.38 سنة) من المحور شبه الرئيسي (0.37 AU).

لذلك، تخضع فينوس لقانون كيبلر الثالث. من أجل الأرض,$P^2 = 1.00 \times 1.00 = 1.00 \text{ year}$ و$a^3 = 1.00 \times 1.00 \times 1.00 = 1.00 \text{ AU}$. تقارب الفترة المدارية (1.00 سنة) (في هذه الحالة، تساوي) المحور شبه الرئيسي (1.00 AU). لذلك، تخضع الأرض لقانون كيبلر الثالث.

التمارين$\PageIndex{1}$

باستخدام الفترات المدارية والمحاور شبه الرئيسية لزحل والمشتري المتوفرة هنا، احسب$P^2$ وتحقق$a^3$ من أنها تخضع لقانون كيبلر الثالث. تبلغ الفترة المدارية لزحل 29.46 عامًا، ومحوره شبه الرئيسي هو 9.54 AU. تبلغ الفترة المدارية لكوكب المشتري 11.86 عامًا، ومحوره شبه الرئيسي هو 5.20 AU.

إجابة

من أجل زحل,$P^2 = 29.46 \times 29.46 = 867.9 \text{ years}$ و$a^3 = 9.54 \times 9.54 \times 9.54 = 868.3 \text{ AU}$. تقترب الفترة المدارية (867.9 سنة) من المحور شبه الرئيسي (868.3 AU). لذلك، يخضع زحل لقانون كيبلر الثالث.

تكريمًا للعالم الذي ابتكر لأول مرة القوانين التي تحكم حركات الكواكب، قرر الفريق الذي بنى أول مركبة فضائية للبحث عن كواكب تدور حول نجوم أخرى تسمية المسبار «كيبلر». لمعرفة المزيد عن حياة يوهانس كيبلر وقوانينه لحركة الكواكب، بالإضافة إلى الكثير من المعلومات حول مهمة كيبلر، قم بزيارة موقع Kepler التابع لناسا واتبع الروابط التي تهمك.

المفاهيم الأساسية والملخص

قدمت ملاحظات تايكو براهي الدقيقة لمواقع الكواكب البيانات التي استخدمها يوهانس كيبلر لاشتقاق قوانينه الأساسية الثلاثة لحركة الكواكب. تصف قوانين كيبلر سلوك الكواكب في مداراتها على النحو التالي: (1) المدارات الكوكبية عبارة عن كتل مع تركيز الشمس على تركيز واحد؛ (2) في فترات متساوية، يكتسح مدار الكوكب مناطق متساوية؛ و (3) العلاقة بين الفترة المدارية ($P$) والمحور شبه الرئيسي ($a$) يتم تحديد المدار بواسطة$P^2 = a^3$ (عندما يكون$a$ بوحدات AU$P$ ويكون بوحدات سنوات الأرض).

مسرد المصطلحات

الوحدة الفلكية (AU)

وحدة الطول المحددة على أنها متوسط المسافة بين الأرض والشمس؛ هذه المسافة حوالي 1.5 × 108 كيلومتر

الانحراف

في الشكل البيضاوي، نسبة المسافة بين البؤر إلى المحور الرئيسي

الشكل البيضاوي

منحنى مغلق يكون فيه مجموع المسافات من أي نقطة على الشكل البيضاوي إلى نقطتين بداخله (تسمى البؤر) هو نفسه دائمًا

التركيز

(صيغة الجمع: البؤر) واحدة من نقطتين ثابتتين داخل الشكل البيضاوي يكون مجموع المسافات إلى أي نقطة على الشكل البيضاوي ثابتًا منها

قانون كيبلر الأول

يتحرك كل كوكب حول الشمس في مدار بيضاوي، مع تركيز الشمس في أحد محاور الشكل البيضاوي

قانون كيبلر الثاني

الخط المستقيم الذي يربط الكوكب والشمس يجتاح مساحات متساوية في الفضاء على فترات زمنية متساوية

قانون كبلر الثالث

يتناسب مربع الفترة المدارية للكوكب بشكل مباشر مع مكعب المحور شبه الرئيسي لمداره

المحور الرئيسي

الحد الأقصى لقطر الشكل البيضاوي

مدار

مسار كائن يدور حول كائن أو نقطة أخرى

الفترة المدارية (P)

الوقت الذي يستغرقه الجسم للسفر مرة واحدة حول الشمس

السرعة المدارية

السرعة التي يدور بها جسم (عادة ما يكون كوكبًا) حول كتلة جسم آخر؛ في حالة الكوكب، السرعة التي يتحرك بها كل كوكب على طول شكله البيضاوي

محور شبه رئيسي

نصف المحور الرئيسي للقسم المخروطي، مثل القطع الناقص