Skip to main content
Global

5.3: גידול אוכלוסייה ורגולציה

  1. Last updated
  2. Save as PDF
  • Page ID
    209200

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    אקולוגים של אוכלוסיות עושים שימוש במגוון שיטות למודל דינמיקת האוכלוסייה. מודל מדויק אמור להיות מסוגל לתאר את השינויים המתרחשים באוכלוסייה ולחזות שינויים עתידיים. שני המודלים הפשוטים ביותר של גידול האוכלוסייה משתמשים במשוואות דטרמיניסטיות (משוואות שאינן מתייחסות לאירועים אקראיים) כדי לתאר את קצב השינוי בגודל האוכלוסייה לאורך זמן. הראשון מבין המודלים הללו, צמיחה אקספוננציאלית, מתאר אוכלוסיות הגדלות במספרים ללא כל הגבלה לצמיחתן. המודל השני, צמיחה לוגיסטית, מציג גבולות לצמיחת הרבייה ההולכים ומתעצמים ככל שגודל האוכלוסייה גדל. אף מודל לא מתאר כראוי אוכלוסיות טבעיות, אך הם מספקים נקודות השוואה.

    קצב גידול האוכלוסייה (r)

    קצב גידול האוכלוסייה (המכונה לפעמים קצב הגידול או קצב הגידול לנפש, ר) שווה לשיעור הילודה (ב) מינוס שיעור התמותה (ד) חלקי גודל האוכלוסייה הראשוני (נ 0).

    r שווה ל- b מינוס d חלקי N קשר

    שיטה נוספת לחישוב קצב גידול האוכלוסייה כוללת גודל אוכלוסייה סופי וראשוני (איור\(\PageIndex{a}\)). במקרה זה, קצב גידול האוכלוסייה (r) שווה לגודל האוכלוסייה הסופי (N) פחות גודל האוכלוסייה ההתחלתי (N 0) ומחולק בגודל האוכלוסייה הראשוני (N 0).

    r שווה קשר N מינוס N מחולק על ידי קשר N

    קאריבו הולך לאורך גוף מים עם שיחים ברקע
    איור\(\PageIndex{a}\): כיצד נוכל לחשב את קצב הגידול של אוכלוסיית הקאריבו הזו בשנה אם היו 200 פרטים בשנת 2016 ו -300 פרטים בשנת 2018? תמונה מאת ק 'ג'ולי/NPS (נחלת הכלל).

    זמן הכפלה

    זמן ההכפלה הוא כמה זמן ייקח לאוכלוסייה להפוך לכפליים מגודלה הראשוני. זמן ההכפלה (t) שווה ל 0.69 חלקי קצב גידול האוכלוסייה (r), שנכתב כפרופורציה.

    t שווה 0.69 חלקי r

    אקולוגים של אוכלוסיות לעיתים מעגלים את המשוואה הזו ומחשבים את זמן ההכפלה באמצעות "כלל 70" (חלוקת 70 בקצב גידול האוכלוסייה, כתוב באחוזים). כדי לבטא את קצב גידול האוכלוסייה כאחוז, הוא מוכפל ב 100%. לפיכך, 0.69 במשוואת זמן ההכפלה המקורית מוכפל גם הוא ב 100. ערך זה (69) מעוגל ל -70 לשם הפשטות.

    צמיחה מעריכית

    צ'ארלס דרווין, בפיתוח תיאוריית הברירה הטבעית שלו, הושפע מהכמורה האנגלי תומאס מלתוס. מלתוס פרסם את ספרו בשנת 1798 וקבע כי אוכלוסיות עם משאבי טבע בשפע גדלות במהירות רבה. עם זאת, הם מגבילים צמיחה נוספת על ידי דלדול המשאבים שלהם. הדפוס המוקדם של האצת גודל האוכלוסייה נקרא גידול מעריכי (איור\(\PageIndex{b}\)).

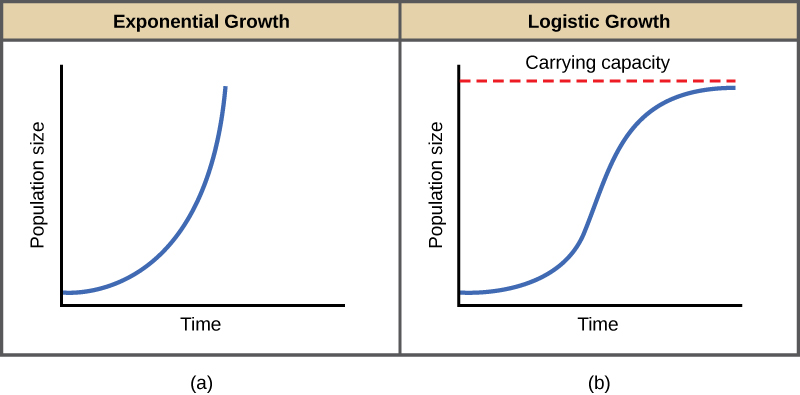
    גרפים של גידול אוכלוסייה מעריכי ולוגיסטי
    איור\(\PageIndex{b}\): גרפים אלה מראים צמיחה מעריכית ולוגיסטית, עם גודל האוכלוסייה על ציר ה- y וזמן על ציר ה- x. כאשר המשאבים אינם מוגבלים, אוכלוסיות מציגות (א) צמיחה מעריכית, המוצגת בעקומה בצורת J. כאשר המשאבים מוגבלים, אוכלוסיות מציגות (ב) צמיחה לוגיסטית. בצמיחה לוגיסטית, התרחבות האוכלוסייה פוחתת ככל שהמשאבים נעשים נדירים, והיא מתיישרת כאשר מגיעים לכושר הנשיאה של הסביבה. עקומת הצמיחה הלוגיסטית היא בצורת S.

    הדוגמה הטובה ביותר לצמיחה מעריכית באורגניזמים נראית בחיידקים. חיידקים הם פרוקריוטים המתרבים במהירות, כשעה עבור מינים רבים. אם מניחים 1000 חיידקים בבקבוק גדול עם אספקה בשפע של חומרים מזינים (כך שהחומרים המזינים לא יתדלדלו במהירות), מספר החיידקים יוכפל מ-1000 ל-2000 לאחר שעה בלבד (איור\(\PageIndex{c}\)). בעוד שעה, כל אחד מ -2000 החיידקים יתחלק וייצר 4000 חיידקים. לאחר השעה השלישית, צריך להיות 8000 חיידקים בבקבוק. התפיסה החשובה של צמיחה מעריכית היא שקצב הגידול - מספר האורגניזמים שנוספו בכל דור רבייה - גדל בעצמו; כלומר, גודל האוכלוסייה גדל בקצב גדול יותר ויותר. לאחר 24 מהמחזורים הללו, האוכלוסייה הייתה גדלה מ -1000 ליותר מ -16 מיליארד חיידקים. כאשר גודל האוכלוסייה, N, משורטט לאורך זמן, נוצרת עקומת צמיחה בצורת J (איור\(\PageIndex{b}\)).

    שתי צלוחיות גדולות עם מרק כהה בתחתית במעבדה
    איור\(\PageIndex{c}\): חיידקים הגדלים עם חומרים מזינים בשפע בבקבוק יציגו צמיחה מעריכית. תמונה מאת סולדד מירנד-רוטמן (CC-BY-SA).

    הדוגמה של חיידקים בבקבוק אינה מייצגת באמת את העולם האמיתי שבו המשאבים בדרך כלל מוגבלים. עם זאת, כאשר מין מוחדר לבית גידול חדש שנראה לו מתאים, הוא עשוי להראות צמיחה מעריכית לזמן מה. במקרה של החיידקים בבקבוק, חלק מהחיידקים ימותו במהלך הניסוי וכך לא יתרבו; לפיכך, קצב הגידול יורד מקצב מקסימלי בו אין תמותה.

    צמיחה לוגיסטית

    צמיחה מעריכית מורחבת אפשרית רק כאשר קיימים משאבי טבע אינסופיים; זה לא המקרה בעולם האמיתי. צ'ארלס דרווין זיהה עובדה זו בתיאורו של "מאבק הקיום", הקובע כי יחידים יתחרו, עם בני מינים משלהם או אחרים, על משאבים מוגבלים. המצליחים נוטים יותר לשרוד ולהעביר את התכונות שגרמו להם להצליח לדור הבא בקצב גדול יותר (ברירה טבעית). כדי לדגמן את המציאות של משאבים מוגבלים, אקולוגים של אוכלוסיות פיתחו את מודל הצמיחה הלוגיסטי.

    בעולם האמיתי, עם המשאבים המוגבלים שלו, הצמיחה האקספוננציאלית לא יכולה להימשך ללא הגבלת זמן. צמיחה אקספוננציאלית עשויה להתרחש בסביבות שבהן יש מעט פרטים ומשאבים בשפע, אך כאשר מספר הפרטים יגדל מספיק, המשאבים יתדלדלו וקצב הצמיחה יאט. בסופו של דבר, קצב הצמיחה יתיישר או יתיישר (איור\(\PageIndex{b}\)). גודל אוכלוסייה זה, שנקבע על ידי גודל האוכלוסייה המרבי שסביבה מסוימת יכולה לקיים, נקרא כושר הנשיאה, המסומל כ - K. באוכלוסיות אמיתיות, אוכלוסייה הולכת וגדלה עולה לעתים קרובות על כושר הנשיאה שלה ושיעור התמותה עולה מעבר לשיעור הילודה וגורם לגודל האוכלוסייה לרדת בחזרה לכושר הנשיאה או מתחתיו. רוב האוכלוסיות בדרך כלל משתנות סביב כושר הנשיאה בצורה גלית ולא קיימות ממש בה.

    גרף של צמיחה לוגיסטית מניב את העקומה בצורת S (איור\(\PageIndex{b}\)). זהו מודל מציאותי יותר של גידול אוכלוסייה מאשר גידול מעריכי. ישנם שלושה חלקים שונים לעקומה בצורת S. בתחילה, הצמיחה היא אקספוננציאלית מכיוון שיש מעט אנשים ומשאבים רבים זמינים. ואז, ככל שהמשאבים מתחילים להיות מוגבלים, קצב הצמיחה יורד. לבסוף, קצב הגידול מתיישר בכושר הנשיאה של הסביבה, עם מעט שינוי במספר האוכלוסייה לאורך זמן.

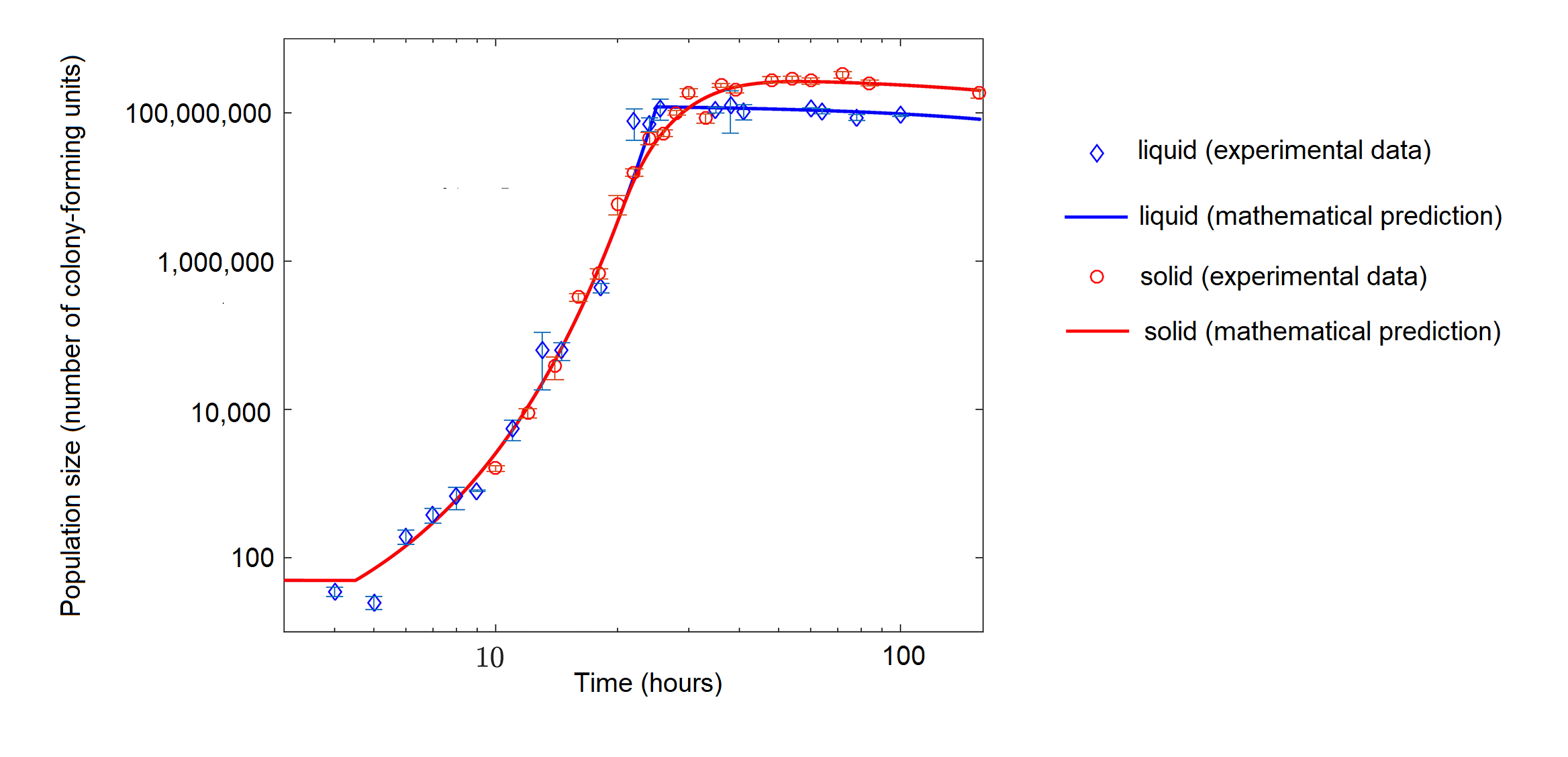
    בעוד שחיידקים בבקבוק עם חומרים מזינים בשפע עשויים להפגין בתחילה צמיחה מעריכית, חיידקים הגדלים עם חומרים מזינים מוגבלים יכולים להפגין צמיחה לוגיסטית (איור\(\PageIndex{d}\)).

    גרף של גודל האוכלוסייה לאורך זמן ב אי - קולי במדיה נוזלית ומוצקה. שניהם נמצאים בסולם יומן.
    איור\(\PageIndex{d}\): צמיחת החיידק Escherichia coli (E. coli) עם חומרים מזינים מוגבלים לאורך זמן בשעות. גודל האוכלוסייה הוא במספר יחידות יוצרות מושבה, שהוא תא המסוגל להתחלק כדי לייצר מושבה של תאים. החיידקים גודלו בנוזל (יהלומים כחולים) או על מדיום מוצק למחצה (אגר, עיגולים אדומים). הנקודות מייצגות מדידות בפועל של גודל האוכלוסיות, והקווים מייצגים מודל מתמטי, בעצם חיזוי המבוסס על נקודות הנתונים. הנתונים מראים גידול אוכלוסיה לוגיסטי, במיוחד במדיה מוצקה. בתחילה, גודל האוכלוסייה גדל במהירות (חלק קעור של העקומה), אך לאחר מכן קצב הגידול מתייצב (קו ישר) לפני ירידה (חלק קמור של העקומה) ויישור ליד כושר הנשיאה. התמונה שונתה משאו X, מוגלר A, קים ג'יי, ג'ונג HJ, לוין BR, Nemenman I (2017) גידול חיידקים במושבות תלת מימדיות. פלוס קומפוט ביול 13 (7): e1005679 (CC-BY).

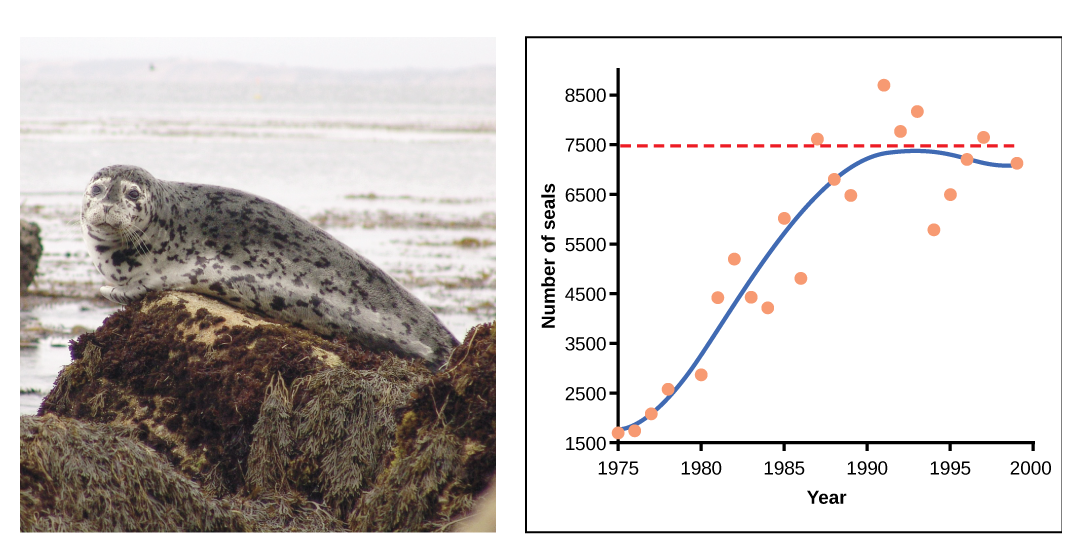
    באוכלוסיות מסוימות, יש וריאציות לעקומה בצורת S. דוגמאות באוכלוסיות בר כוללות כבשים וכלבי ים (איור\(\PageIndex{e}\)). בשתי הדוגמאות, גודל האוכלוסייה עולה על כושר הנשיאה לפרקי זמן קצרים ואז נופל מתחת לכושר הנשיאה לאחר מכן. תנודה זו בגודל האוכלוסייה ממשיכה להתרחש כאשר האוכלוסייה מתנדנדת סביב כושר הנשיאה שלה. ובכל זאת, אפילו עם תנודה זו המודל הלוגיסטי מאושר.

    חותם (משמאל) וגרף של גידול אוכלוסייה לוגיסטי (מימין)
    איור\(\PageIndex{e}\): אוכלוסייה טבעית של כלבי ים מראה צמיחה לוגיסטית. מספר החותמות, שנע בין 1500 ל 8500, הוא על ציר ה- y, והשנה, שנעה בין 1975-2000, נמצאת על ציר ה- x. נקודות כתומות מייצגות את גודל האוכלוסייה הנצפה מדי שנה, והקו הכחול מייצג את המגמה. בשנים 1975 עד 1983, הקו הכחול מתעקל כלפי מעלה, המייצג עלייה הן בגודל האוכלוסייה והן בקצב גידול האוכלוסייה. משנת 1983 עד 1992 העקומה משתטחת, מה שמייצג שגודל האוכלוסייה עדיין גדל, אך קצב גידול האוכלוסייה יורד. לאחר 1992, האוכלוסייה משתנה ליד כושר הנשיאה (קו מקווקו, אופקי).

    מודל גידול האוכלוסייה הלוגיסטי אינו הדרך היחידה שבה אוכלוסיות מגיבות למשאבים מוגבלים. באוכלוסיות מסוימות, הצמיחה היא אקספוננציאלית עד שהמשאבים אוזלים, הפסולת מצטברת או התפשטות המחלה (ראה גורמים מגבילים להלן), ואז האוכלוסייה מתרסקת. לפיכך, קצב גידול האוכלוסייה (וגודל) עשוי לצנוח במהירות במקום להתחדד ככל שהוא מתקרב לכושר הנשיאה.

    דינמיקת אוכלוסייה ורגולציה

    המודל הלוגיסטי של גידול האוכלוסייה, למרות שהוא תקף באוכלוסיות טבעיות רבות ומודל שימושי, הוא פישוט של דינמיקת האוכלוסייה בעולם האמיתי. המשתמע במודל הוא שיכולת הנשיאה של הסביבה אינה משתנה, וזה לא המקרה. כושר הנשיאה משתנה מדי שנה. לדוגמה, חלק מהקיצים חמים ויבשים ואילו אחרים קרים ורטובים; באזורים רבים כושר הנשיאה במהלך החורף נמוך בהרבה מאשר בקיץ. יתר על כן, גורמים מסוימים (גורמי גדילה) מגדילים את קצב גידול האוכלוסייה בעוד שגורמים אחרים (גורמים מגבילים) מאטים את גידול האוכלוסייה. דוגמאות לגורמי גדילה הם משאבים כמו מזון, מים וחלל. ניתן לסווג גורמים מגבילים כתלויים בצפיפות או בלתי תלויים בצפיפות.

    תקנה תלויה בצפיפות

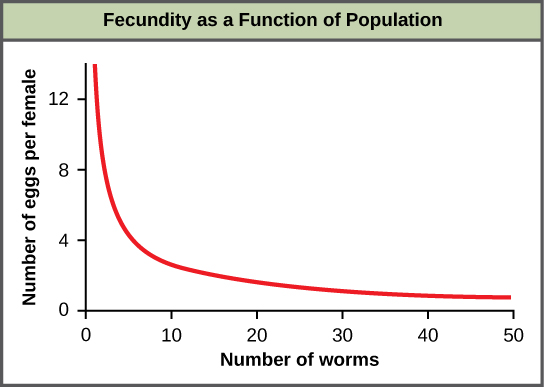
    רוב הגורמים התלויים בצפיפות הם ביולוגיים באופיים (ביוטיים). בדרך כלל, ככל שהאוכלוסייה צפופה יותר, כך שיעור התמותה שלה גדול יותר. דוגמה לוויסות תלוי צפיפות מוצגת באיור \(\PageIndex{f}\) עם תוצאות ממחקר המתמקד בתולעת המעי העגולה הענקית (Ascaris lumbricoides), טפיל של בני אדם ויונקים אחרים. אוכלוסיות צפופות יותר של הטפיל הפגינו פוריות נמוכה יותר: הן הכילו פחות ביצים. הסבר אפשרי לכך הוא שהנקבות יהיו קטנות יותר באוכלוסיות צפופות יותר (בגלל משאבים מוגבלים) וכי לנקבות קטנות יותר יהיו פחות ביציות. השערה זו נבדקה והופרכה במחקר משנת 2009 שהראה כי למשקל הנשי אין השפעה. הסיבה האמיתית לתלות בצפיפות הפריון באורגניזם זה עדיין לא ברורה וממתינה להמשך חקירה.

    גרף הפריון כפונקציה של חלקות אוכלוסייה מספר ביציות לנקבה לעומת מספר תולעים.
    איור\(\PageIndex{f}\): באוכלוסייה זו של תולעים עגולות, הפריון (מספר הביציות לנקבה) יורד עם גודל האוכלוסייה (מספר התולעים). (שים לב שגודל האוכלוסייה ולא צפיפות האוכלוסייה מוצג כאן, אך צפיפות האוכלוסייה אכן מתואמת עם גודל האוכלוסייה.) מספר הביציות יורד במהירות בהתחלה, ואז יורד בין 30 ל -50 תולעים.

    גורמים תלויי צפיפות כוללים טריפה, טפילות, אוכלי עשב, תחרות והצטברות פסולת. ככל שהאוכלוסייה גדלה, טורפיה מסוגלים לקצור אותה ביתר קלות. צפיפות הטרף משפיעה גם על קצב גידול האוכלוסייה של טורפים: צפיפות טרף נמוכה מגדילה את התמותה של הטורף שלו מכיוון שהוא מתקשה יותר לאתר את מקורות המזון שלו.

    טפילים מסוגלים לעבור ממארח למארח ביתר קלות ככל שצפיפות האוכלוסייה של המארח עולה. מסיבה זו, מגיפות בקרב בני אדם חמורות במיוחד בערים. למעשה, במשך רוב התקופה מאז החלו בני האדם להתגורר בערים, אוכלוסיות הערים נשמרו רק באמצעות הגירה מתמשכת מהכפר. רק לאחר התפתחות התברואה הקהילתית, החיסונים ואמצעי בריאות הציבור האחרים נמנעו ערים מירידות חדות תקופתיות באוכלוסייה כתוצאה ממגפות. המגיפות החוזרות ונשנות של "המוות השחור" באירופה שהחלו במאה הארבע עשרה גרמו לירידה חדה באוכלוסייה. בתוך שלוש שנים בלבד (1348—1350), לפחות רבע מאוכלוסיית אירופה מתה מהמחלה (כנראה מגיפה).

    באופן דומה, אוכלי עשב יכולים להתפשט ביתר קלות בין צמחים בודדים באוכלוסייה צפופה. זו הסיבה שחיתוך רצועות (ראה חקלאות בת קיימא) מסייע בהדברת מזיקים. אוכלי עשב או פתוגן צמחי עשויים להדביק שורה אחת של צמחים, אך יש פחות סיכוי להתפשט לשורות רחוקות יותר מאותו מין.

    בעוד שמתרחשת תחרות בין-ספציפית בין מינים שונים, תחרות תוך-ספציפית מתרחשת כאשר בני אותו מין פוגעים זה בזה על ידי שימוש באותם משאבים. לדוגמה, בקיץ 1980, חלק גדול מדרום ניו אינגלנד נפגע מהתפשטות של עש הצועני (איור\(\PageIndex{g}\)). ככל שהקיץ חלף, הזחלים (הזחלים) התגלמו, המבוגרים שבקעו הזדווגו, הנקבות הטילו המוני ביצים (כל מסה מכילה כמה מאות ביצים) כמעט על כל עץ באזור. בתחילת מאי 1981 החלו הזחלים הצעירים שבקעו מביצים אלה להאכיל ולהתמוסס.

    זחל עש צועני על גזע עץ
    איור\(\PageIndex{g}\): זחלי עש צועני מתמודדים עם תחרות תוך ספציפית בצפיפות גבוהה. תמונה על ידי עורך בגדול (CC-BY-SA).

    התוצאות היו דרמטיות: תוך 72 שעות, עץ אשור בגובה 50 רגל או עץ אורן לבן בגובה 25 רגל יפורק לחלוטין. כתמי יער גדולים החלו לקבל מראה חורפי עם שלדי הענפים החשופים שלהם. למעשה, הנגיעות הייתה כה כבדה עד שעצים רבים התפזרו לחלוטין לפני שהזחלים הצליחו להשלים את התפתחות הזחל שלהם. התוצאה: מוות מסיבי של בעלי החיים; מעטים מאוד הצליחו להשלים מטמורפוזה. כאן, אם כן, הייתה דוגמה דרמטית לאופן שבו התחרות בין בני מין אחד על משאב סופי - במקרה זה, מזון - גרמה לירידה חדה באוכלוסייה. ההשפעה הייתה תלויה בבירור בצפיפות. צפיפות האוכלוסייה הנמוכה יותר בקיץ הקודם אפשרה לרוב בעלי החיים להשלים את מחזור חייהם.

    תקנה בלתי תלויה בצפיפות

    גורמים בלתי תלויים בצפיפות, בדרך כלל פיזיים או כימיים באופיים (אביוטי), משפיעים על תמותה של אוכלוסייה ללא קשר לצפיפותה, כולל מזג אוויר (איור\(\PageIndex{h}\)), אסונות טבע (רעידות אדמה, הרי געש, שריפות וכו ') וזיהום. צבי בודד עלול להיהרג בשריפת יער ללא קשר לכמה צבאים נמצאים באזור זה. סיכויי ההישרדות שלה זהים בין אם צפיפות האוכלוסייה גבוהה או נמוכה. הדבר נכון גם לגבי מזג אוויר חורפי קר.

    נוף לוויני של הוריקן פירנצה, המופיע כספירלה לבנה
    איור\(\PageIndex{h}\): מזג אוויר קשה, כמו הוריקן פירנצה משנת 2018, יכול להפחית את גודל האוכלוסייה ללא קשר לצפיפות. תמונה על ידי מרכז טיסות החלל גודארד של נאס"א (CC-BY)

    במצבים אמיתיים, ויסות האוכלוסייה מסובך מאוד וגורמים תלויי צפיפות ועצמאיים יכולים לקיים אינטראקציה. אוכלוסייה צפופה המופחתת באופן בלתי תלוי בצפיפות על ידי גורמים סביבתיים כלשהם תוכל להתאושש בצורה שונה מאוכלוסייה דלילה. לדוגמה, אוכלוסיית צבאים שנפגעו מחורף קשה תתאושש מהר יותר אם יישארו עוד צבאים להתרבות.

    ייחוסים

    שונה על ידי מליסה הא מהמקורות הבאים: