Skip to main content
Global

8.2: להבין את הנתונים

  1. Last updated
  2. Save as PDF
  • Page ID
    207096

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    מטרות למידה

    בסוף פרק זה, תוכל:

    • זיהוי סוגים שונים של גרפים
    • הסבר את מדדי הנטייה המרכזית, כולל מצב, חציון וממוצע
    • להבין מדדי פיזור, כולל סטייה, שונות וסטיית תקן

    במחקר מדעי המדינה, כמה חוקרים מתעניינים בעיקר בתיאור העולם בעוד שאחרים מעוניינים להסביר תופעה מסוימת בעולם. במילים אחרות, מחקר מדעי המדינה כולל מטרות כפולות של תיאור והסבר. חשוב לציין כי מלאכת התיאור וההסבר הינה אינטראקטיבית באופייה, ולעתים קרובות הם ניזונים זה מזה. עם זאת, ברוב המקרים, ראשית עלינו לדעת משהו על העולם לפני שנצא למשימה להסביר משהו שקורה בעולם ההוא. בחלק זה נחקור את הטכניקות השונות לסיכום הנתונים.

    בין אם אוספים נתונים מקוריים או מרכיבים מערך נתונים המבוסס על מקורות נתונים קיימים, הצעד הראשון הוא לארגן את הנתונים הגולמיים לפורמט הניתן לניהול יותר. ג'ונסון, ריינולדס ומיקוף (2020) מציעים להמיר תחילה נתונים גולמיים למטריצת נתונים שבה כל שורה מייצגת ערך ייחודי וכל עמודה מייצגת משתנים שונים (ראה טבלה 8-2). בעוד פורמט זה של ארגון נתונים מאפשר לחוקרים לראות בבירור מידע על כל תצפית ולהשוות כמה תצפיות, הוא אינו הפורמט המתאים ביותר לסיכום הנתונים כך שהחוקר יוכל לתפוס את המידע הכללי על העולם בו היא מעוניינת.. אז מהו הפורמט הנכון בהצגת נתונים מספריים לתיאור המידע שחוקר מעוניין בו? הכל תלוי ברמת המדידה של המשתנים (כלומר, נומינלי, סדיר, מרווח ויחס) שמערך הנתונים שלך כולל.

    טבלה 8.1
    מחוז שיעור אבטלה תוחלת חיים טמפרטורה גבוהה ממוצעת (צלזיוס) השפה הנפוצה ביותר

    בלגיה

    		 7 81 6 הולנדית
    צרפת 10 82 7 צרפתי
    אירלנד 6 81 8 אנגלי
    לוקסמבורג 6 82 2 לוקסמבורגית
    מונקו 2 89 13 צרפתי
    הולנד 5 81 6 הולנדית
    הממלכה המאוחדת 4 81 8 אנגלי

    חשוב לציין כי ייצוג נתונים בפורמט טבלה כשלעצמו לא היה החסרונות של טבלה 8-2. זה היה סוג המידע הכלול בטבלה היה הנושא כאן במטרה של הטבלה היה להציג מידע סיכום על הנתונים שנצפו כאן. לעתים קרובות, אנו מתייחסים לזה כאל סטטיסטיקה תיאורית, או ייצוג מספרי של מאפיינים ומאפיינים מסוימים של כל הנתונים שנאספו. מטרת טבלת הסטטיסטיקה התיאורית היא פשוט להציג מספרים המתארים את המקרים, או את המאפיינים הבסיסיים של הנתונים במחקר. תסתכל על טבלה 8-3 להלן. זוהי דוגמה לטבלת תדרים הכוללת תדירות, פרופורציה, אחוז ואחוז מצטבר של תצפית מסוימת. אפילו בטבלה זו, חלקם שימושיים יותר מבחינת הבנת תצפית מסוימת אחת ביחס לשאר העולם שמעוניינים לתאר ולהסביר. פרופורציה ואחוז (מדדי תדירות יחסית) מאפשרים לנו לבצע השוואה בקלות בין תצפיות שונות על אותו משתנה.

    טבלה 8.2: חלוקת תדרים: שדה תעופה במדינות מערב אירופה
    מחוז תדירות פרופורציה אחוז אחוז מצטבר
    בלגיה 41 0.04 4 4
    צרפת 464 0.45 45 49
    אירלנד 40 0.04 4 53
    לוקסמבורג 2 0.00 0 53
    מונקו 0 0.00 0 53
    הולנד 29 0.03 3 56
    הממלכה המאוחדת 460 0.44 44 100
    סך הכל 1036 1.00 100  

    מקור: ג'ונסון, ריינולדס ומיקוף (2015) 020)

    ניתן להציג התפלגות תדרים עבור משתנה כמותי בפורמט גרף הנקרא היסטוגרמה. זהו סוג של גרף כאן הגובה והשטח של הסורגים פרופורציונליים לתדרים בכל קטגוריה של משתנה. ניתן להשתמש בהיסטוגרמה למשתנה מרווח או יחס עם מספר גדול יחסית של מקרים. עבור משתנים קטגוריים (סדירים או נומינליים), חוקר יכול להציג את התאריך בצורה דומה עם גרף עמודות. גרף עמודות הוא ייצוג חזותי של הנתונים, המצויר בדרך כלל באמצעות פסים מלבניים כדי להראות עד כמה כל ערך גדול. הסורגים יכולים להיות אנכיים או אופקיים. בהתחשב באופי הנתונים הסדירים או הנומינליים, גרף עמודות עוסק במספר קטן בהרבה של קטגוריות מאשר בן דודו ההיסטוגרמה העוסק בנתוני מרווחים או יחס.

    צילום מסך 2020-11-16 בשעה 2.00.13 PM.png

    אם חוקר מעוניין להציג קשר בין שני משתנים בפורמט גרפי, פיזור יהיה בחירה מצוינת. צורת גרף זו משתמשת בקואורדינטות קרטזיות (כלומר, מישור המורכב מציר x וציר y) כדי להציג ערכים לשני משתנים ממערך נתונים כדי להציג כיצד משתנה אחד עשוי להשפיע על המשתנה השני.

    צילום מסך 2020-11-16 בשעה 2.00.31 PM.png

    מדעני החברה, באופן כללי, ומדענים וכלכלנים פוליטיים מתעניינים לעתים קרובות במגמה של משתנה לאורך זמן. ניתן להשתמש בעלילת סדרת זמן כדי להציג את השינויים בערכים של משתנה הנמדד בנקודה אחרת בהיסטוריה. עבור גרף זה, ציר ה- x מייצג את משתנה הזמן (למשל, חודשים, שנה וכו ') וציר ה- y מייצג את משתנה הריבית. בניגוד לפיזור, כל נקודה (תצפית) מחוברת זו לזו כדי להציג את השינויים בערך משתנה העניין. אנו יכולים, למשל, להציג את מספר התיקונים החוקתיים המוצעים בארצות הברית מאז מציאתה או את מספר הנשים בקונגרס האמריקאי לאורך השנים. בדוגמה האחרונה, אנו יכולים להשתמש בשני קווים כדי להבדיל בין נוכחותן של נציגות בבית הנבחרים ובסנאט באמצעות שני קווים נפרדים באותו מישור גרפי.

    צילום מסך 2020-11-16 בשעה 3.03.46 PM.png

    כאמור, חוקרים יכולים לתאר את הנתונים על ידי הסתמכות על נתונים סטטיסטיים תיאוריים. נתונים סטטיסטיים תיאוריים הם הייצוג המספרי של מאפיינים ומאפיינים מסוימים של כל הנתונים שנאספו. אחת המטרות העיקריות של סטטיסטיקה תיאורית היא "לחקור את הנתונים ולצמצם אותם למונחים פשוטים ומובנים יותר מבלי לעוות או לאבד חלק ניכר מהמידע הזמין". (אגרסטי ופינליי 1997). הנתונים הסטטיסטיים התיאוריים הנפוצים ביותר הם מידע שמאתר את מרכז או אמצע הפצת הנתונים ומידע על אופן הפצת הנתונים ביחס למרכז הממוקם.

    מדדים של נטייה מרכזית - המצב, החציון והממוצע - מאתרים את מרכז ההתפלגות של מערך נתונים מסוים. במילים אחרות, מדד לנטייה מרכזית מזהה את "המקרה האופייני ביותר" באותה הפצת נתונים. ראשית, המצב הוא הקטגוריה עם התדר הגבוה ביותר. שנית, החציון הוא הנקודה בהתפלגות המפצלת את התצפיות לשני חלקים שווים. זוהי נקודת האמצע של חלוקת הנתונים כאשר התצפיות מסודרות לפי הערכים המספריים שלהן. אם יש מספרים מוזרים של תצפיות בנתונים, המדידה היחידה באמצע היא החציון. במקרה של מספר זוגי של תצפיות, הערך הממוצע של שתי המדידות האמצעיות הוא החציון. לבסוף, הממוצע או הממוצע הם אולי הדרך הנפוצה ביותר לזהות את מרכז ההתפלגות. זהו סכום הערך הנצפה של כל נושא חלקי מספר הנבדקים. זה יכול לבוא לידי ביטוי באופן רשמי יותר:

    \[Y_underbar = \dfrac{ΣY_i}{n} \label{8.1}\]

    כאשר \(Y_underbar\) מייצג את הממוצע (הממוצע), \(Σ\) האמצעים \(Y_1 + Y_2 + ... Y_n\) \(Y\) הם מדידות של כל תצפית \(n\) ומייצג את מספר התצפיות. לדוגמה, אם ישנם 5 תלמידים עם ציוני בחינות אמצע טווח של 80, 77, 91, 62 ו- 85, n = 5 ו- = 395 (הוסף את כל ציון המבחן). הציון הממוצע לבחינת אמצע זה הוא 3955, שהוא 79.

    בנוסף למדדים של נטיות מרכזיות, חוקרים מסתמכים לעתים קרובות על מדד השתנות הנתונים כדי להבין היטב את הנתונים המשמשים במחקר שלהם. אולי המדידה הפשוטה ביותר של שונות הנתונים היא הטווח. הטווח הוא ההפרש בערך בין הערך המקסימלי למינימום. לדוגמה, אם ציון מבחן האמצע הגבוה ביותר בכיתה היה 100 והציון הנמוך ביותר היה 70, הטווח עבור מערך הנתונים הספציפי הזה הוא 100 - 70 = 30. מדידה נוספת הקשורה לשונות נקראת הטווח הבין-רבעוני או IQR. ה- IQR הוא ההבדל בין האחוזון ה -75 (כאשר 75% מהערכים ממוקמים מתחת לאותה נקודה) לבין האחוזון ה -25 (כאשר 25% מהתצפיות נמצאות מתחת לנקודה זו). במילים אחרות, ה- IQR הוא הטווח בו הערכים המקסימליים הוא הרבעון השלישי (Q3) והערכים המינימליים הם הרבעון הראשון (Q1) מדידה זו מספרת לנו עד כמה התפשטות 50% האמצעיים מהתצפיות. כמה חוקרים משתמשים בעלילת קופסה כדי להציג בצורה גרפית, רבעונים והחציון

    דרך נוספת למדידת פיזור הנתונים היא לבחון עד כמה התצפיות הכלולות רחוקות מהממוצע. המרחק של תצפית מהממוצע נקרא סטייה. השונות מוגדרת בפשטות כממוצע הסטייה בריבוע. כדי לחשב שונות, תחילה מודדים את המרחק של כל תצפית מהממוצע ומרובעים אותם. הוסף את כל הסטיות בריבוע וחלק אותה במספר התצפיות (לשונות האוכלוסייה) או חלק אותה במספר התצפיות מינוס אחת (לשונות מדגם). אנו מציינים שונות באמצעות σ 2 (מבוטא sigma בריבוע).

    שונות אוכלוסין:

    \[σ^2 = \dfrac{Σ(Y_i - μ)^2}{N} \label{8.2}\]

    שונות לדוגמא:

    \[σ^2= \dfrac{ΣY_i Y_underbar}{n-1} \label{8.3}\]

    במשוואה\ ref {8.2}, μ (מבוטא mu) הוא ממוצע האוכלוסייה (או הממוצע) של משתנה \(Y\) \(Y_i\) ומייצג כל תצפית. המשוואה שונה במקצת עבור שונות המדגם (משוואה\ ref {8.3}). לעשות זאת ביד זה מייגע למדי עבור נתונים עם אוכלוסייה גדולה או מדגם. כתוצאה מכך חוקרים רבים מסתמכים על תוכנות ניתוח סטטיסטיות שונות או גיליונות אלקטרוניים כמו Excel.

    סטיית התקן היא השורש הריבועי של השונות. הוא מייצג את סטיית התצפית האופיינית לעומת המרחק הממוצע בריבוע מהממוצע.

    שונות אוכלוסין:

    \[σ^2 = \dfrac{Σ(Y_i - μ)^2}{N} \label{8.4}\]

    שונות לדוגמא:

    \[σ^2= \dfrac{ΣY_i Y_underbar}{n-1} \label{8.5}\]

    סטיית התקן שימושית בפירוש נוסף של הנתונים העומדים על הפרק. בדרך כלל, כ -68% מהתצפיות נופלות בסטייה הראשונה מהממוצע. מה זה אומר? ובכן, הבה נבחן את הדוגמה הבאה. הפרופסור שלך למדעי המדינה אומר לך שהציון הממוצע/ממוצע לבחינה שעשית זה עתה היה 85 עם סטיית התקן של 5. המשמעות היא שהציונים של 68% מהתלמידים נופלים בין 80 - הממוצע של 85 פחות סטיית התקן של 5 - ו 90 - הממוצע של 85 פלוס סטיית התקן של 5. חשוב לציין כי תצפית חורגת מהממוצע בכיוונים חיוביים ושליליים כאחד.

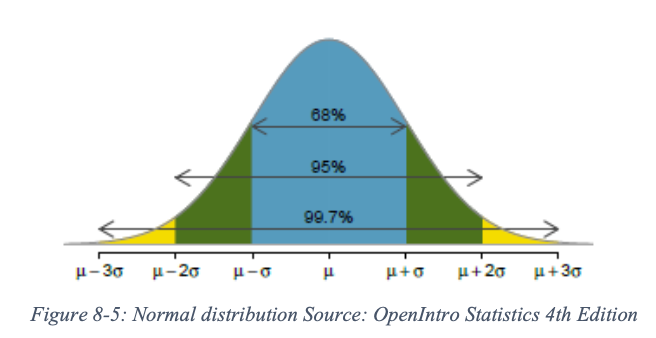
    צילום מסך 2020-11-16 בשעה 3.16.49 PM.png

    כפי שמראה איור 8.1, כ -95% מהנתונים נופלים בסטיית התקן השנייה. המשמעות היא שאז 95% מציוני הבחינה צריכים לרדת בין 75 ל 95. אז אם קלעתם 96 בבחינה זו, מה נוכל לומר על הציון שלכם? ובכן, אתה יכול לומר שעשית טוב מאוד מכיוון שהציון שלך הוא מעבר לסטייה השנייה, מה שאומר שיש רק פחות מ -5% מהאנשים שקיבלו ציון גבוה ממך. במילים אחרות, ישנם כ -95% מבני גילך שקיבלו ציון נמוך מהציון שלך.

    בחלק הבא, נבנה על התוכן של סעיף זה ונחקור את האמצעים לבדיקת הקשר.