4.1: עקרונות בסיסיים של קטליזה
- Page ID
- 207572
גרסה להדפסה של סעיף זה נמצאת כאן: BiochemFFA_4_1.pdf. ספר הלימוד כולו זמין בחינם מהמחברים בכתובת http://biochem.science.oregonstate.edu/content/biochemistry-free-and-easy
אם יש מרכיב קסום לחיים, בוודאי ניתן לטעון שמדובר בקטליזה. הודות לקטליזה, תגובות שיכולות להימשך מאות שנים להשלים ב"עולם האמיתי "הבלתי מזורז, מתרחשות תוך שניות בנוכחות זרז. זרזים כימיים, כגון פלטינה, יכולים להאיץ תגובות, אך אנזימים (שהם פשוט זרזים-על עם "טוויסט", כפי שנראה) מבייש זרזים כימיים (איור 4.1). כדי להבין קטליזה אנזימטית, יש צורך קודם להבין אנרגיה. תגובות כימיות עוקבות אחר המגמה האוניברסלית של התקדמות לעבר אנרגיה נמוכה יותר, אך לעיתים קרובות יש להן מחסום שיש להתגבר עליו. הסוד לפעולה קטליטית הוא הפחתת גודל המחסום הזה.
לפני דיון באנזימים, ראוי להשהות ולדון במושג חשוב הנוגע לתגובות כימיות/ביוכימיות. מושג זה הוא שיווי משקל ולעתים קרובות הוא לא מובן. החלק "equi" של המילה מתייחס לשווה, כפי שניתן לצפות, אך הוא אינו מתייחס לריכוזים מוחלטים. מה שקורה כאשר תגובה ביוכימית נמצאת בשיווי משקל הוא שריכוזי המגיבים והתוצרים אינם משתנים עם הזמן. זה לא אומר שהתגובות נפסקו. זכור שהתגובות הן הפיכות, כך שיש תגובה קדימה ותגובה הפוכה: אם היו לך 8 מולקולות של A, ו -4 של B בהתחלה, ו-2 מולקולות של A הומרו ל-B, בעוד ש-2 מולקולות של B הומרו בו זמנית בחזרה ל-A, מספר המולקולות של A ו-B נשאר ללא שינוי, כלומר, התגובה נמצאת בשיווי משקל. עם זאת, תבחין כי אין זה אומר שיש מספר שווה של מולקולות A ו- B.
ענייני ריכוז
לכן, בניגוד לתפיסתם של תלמידים רבים, ריכוזי המוצרים והמגיבים אינם שווים בשיווי משקל, אלא אם כן ΔG °' לתגובה הוא אפס, כי כשזה המקרה,
\[ΔG = \ln \left(\dfrac{[\rm{Products}]}{[\rm{Reactants}]} \right)\]
מכיוון שה- ΔG° 'הוא אפס. מכיוון ש- ΔG עצמו הוא אפס בשיווי משקל, אם כן
\[[Products] = [Reactants].\]
זה המצב היחיד שבו
\[[Products] = [Reactants]\]
בשיווי משקל. חוזרים על עצמם, בשיווי משקל, ריכוזי המגיב והמוצר אינם משתנים עם הזמן. כלומר, עבור תגובה \(A \rightleftharpoons B [A]\) בזמן אפס כאשר מגיעים לשיווי משקל,\([A]_{T_0}\), תהיה זהה כעבור 5 דקות (בהנחה ש- A ו- B יציבים כימית). לפיכך,
\[[A]_{T_0} = [A]_{T+5}\]
באופן דומה,
\[[B]_{T_0} = [B]_{T+5}\]
לצורך העניין, בכל פרק זמן X לאחר שהושג שיווי המשקל,
\[[A]T0 = [A]T+5 = [A]TX\]
ו
\[[B]T0 = [B] T+5 = [B]TX\]
עם זאת, אלא אם כן ΔG°' = 0, לא נכון לומר [A] T0 = [B] T0 כאשר אנו חוקרים תגובות ביוכימיות ושיעורי תגובה, חשוב לזכור כי 1) תגובות אינן מתחילות בדרך כלל בשיווי משקל; 2) כל התגובות נעות לכיוון שיווי המשקל; ו-3) תגובות בתאים מתנהגות בדיוק כמו אלה שבמבחנות - הן לא מתחילות בשיווי משקל, אלא הן נעות לעברו. תגובות דינמיות התגובות המתרחשות בתאים, עם זאת, הן דינמיות ומורכבות מאוד. במבחנה ניתן ללמוד אותם אחד בכל פעם. בתאים, התוצר של תגובה אחת הוא לרוב המצע לתגובה אחרת. תגובות בתאים קשורות זו בזו זו, מה שמוליד את מה שמכונה מסלולים מטבוליים. יש, למעשה, אלפי תגובות מקושרות שונות המתרחשות ברציפות בתאים.
ניסיונות לחקור תגובה אחת בתוהו ובוהו של תא מרתיעים בלשון המעטה. מסיבה זו, ביוכימאים מבודדים אנזימים מהתאים וחוקרים תגובות בנפרד. מתוך מחשבה זו אנו מתחילים את שיקולנו את תופעת הקטליזה על ידי תיאור, ראשית, את אופן הפעולה של אנזימים.
אנרגיית הפעלה
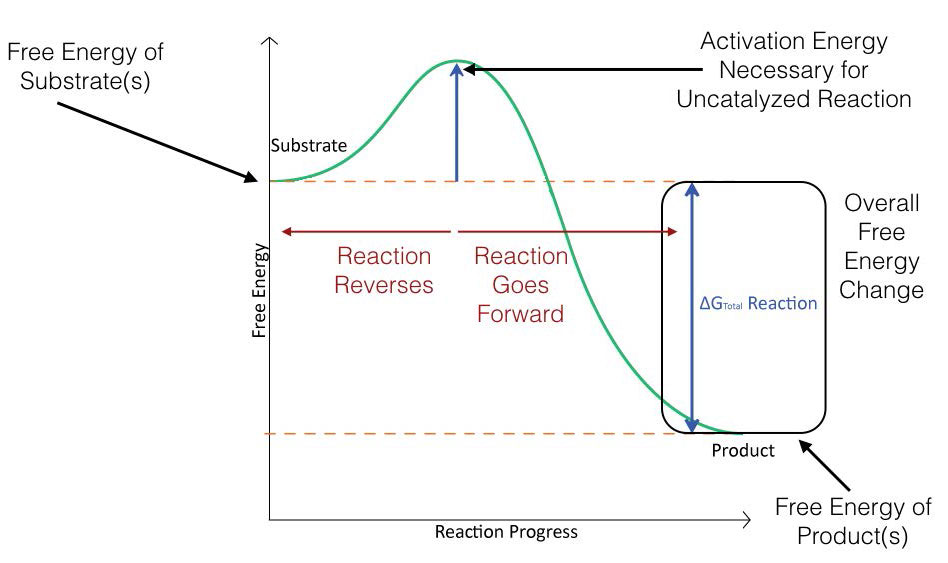
איור 4.2 מתאר באופן סכמטי את שינויי האנרגיה המתרחשים במהלך התקדמות תגובה פשוטה. על מנת שהתגובה תמשיך, יש להתגבר על אנרגיית הפעלה על מנת שהתגובה תתרחש.
באיור 4.3, אנרגיית ההפעלה לתגובה מזורזת מכוסה. כפי שאתה יכול לראות, המגיבים מתחילים באותה רמת אנרגיה הן לתגובות מזורזות והן לתגובות לא מזורזות וכי התוצרים מסתיימים באותה אנרגיה גם עבור שניהם. לתגובה המזורזת, לעומת זאת, יש אנרגיית הפעלה נמוכה יותר (קו מקווקו) מאשר התגובה הבלתי מזורזת. זהו סוד הקטליזה - ΔG הכולל לתגובה אינו משתנה עם קטליזה, אך אנרגיית ההפעלה יורדת.
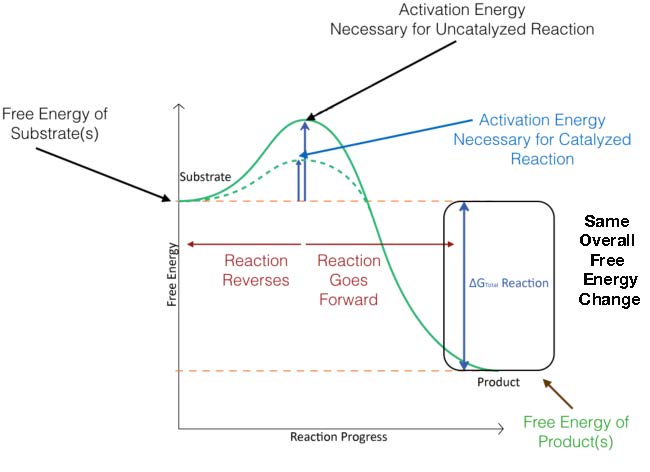
איור 4.3 - שינויים באנרגיה במהלך תגובה לא מזורזת (קו ירוק מלא) ותגובה מזורזת (קו ירוק מנוקד). תמונה על ידי אליה קים
הפיכות
המידה שבה התגובות יתקדמו קדימה היא פונקציה של גודל הפרש האנרגיה בין המוצר למצבי המגיבים. ככל שהאנרגיה של המוצרים נמוכה יותר בהשוואה למגיבים, כך גדל אחוז המולקולות שיהיו כמוצרים בשיווי משקל. ראוי לציין שמכיוון שאנזים מוריד את אנרגיית ההפעלה לתגובה הוא יכול להאיץ את היפוך התגובה בדיוק כפי שהוא מאיץ תגובה בכיוון קדימה. בשיווי משקל, כמובן, לא מתרחש שינוי בריכוז המגיבים והתוצרים. לפיכך, אנזימים מאיצים את הזמן הנדרש כדי להגיע לשיווי משקל, אך אינם משפיעים על מאזן המוצרים והמגיבים בשיווי משקל.
חריגים
הפיכות התגובות האנזימטיות היא שיקול חשוב לשיווי משקל, למדידת קינטיקה של האנזים, לאנרגיה החופשית של גיבס, למסלולים מטבוליים ולפיזיולוגיה. עם זאת, ישנם כמה חריגים קלים להפיכות התגובות. הם קשורים להיעלמות מצע או תוצר של תגובה. שקול את התגובה הראשונה שמתחתיה מזורזת על ידי האנזים פחמן אנהידראז:
\[CO_2 + H_2O \rightleftharpoons H_2CO_3 \rightleftharpoons HCO_3^- + H^+\]
בכיוון קדימה, חומצה פחמנית מופקת ממים ופחמן דו חמצני. זה יכול להישאר שלם בתמיסה או ליינן כדי לייצר יון ביקרבונט ופרוטון. בכיוון ההפוך, מים ופחמן דו חמצני מיוצרים. פחמן דו חמצני, כמובן, הוא גז ויכול לעזוב את התמיסה ולברוח.
כאשר מולקולות תגובה מוסרות, כפי שיהיו אם פחמן דו חמצני בורח, התגובה נמשכת לכיוון המולקולה שאובדת והיפוך לא יכול להתרחש אלא אם כן מוחלפת המולקולה החסרה. בתגובה השנייה המתרחשת מימין, חומצה פחמנית (H2שיתוף3) "מוסרת" על ידי יינון. גם זה יגביל את התגובה חזרה לפחמן דו חמצני במים. סוג אחרון זה של "הסרה" הוא המתרחש במסלולים מטבוליים. במקרה זה, תוצר של תגובה אחת (חומצה פחמנית) הוא המצע הבא (היווצרות של ביקרבונט ופרוטון).
במסלול המטבולי של הגליקוליזה, עשר תגובות מחוברות בצורה זו והיפוך התהליך הרבה יותר מסובך מאשר אם נשקלת רק תגובה אחת.
מנגנוני פעולה כלליים
כפי שצוין לעיל, תגובות מזורזות אנזימטית הן בסדרי גודל מהירים יותר מתגובות לא מזורזות וכימיות. סוד הצלחתם טמון בהבדל מהותי במנגנוני הפעולה שלהם.
כל סטודנט לכימיה לימד שזרז מזרז תגובה מבלי שנצרך על ידה. במילים אחרות, הזרז מסתיים לאחר תגובה בדיוק כפי שהתחיל כך שהוא יכול לזרז גם תגובות אחרות. אנזימים חולקים תכונה זו, אך באמצע, במהלך הפעולה הקטליטית, אנזים משתנה באופן זמני. למעשה, יכולתו של אנזים להשתנות היא שמובילה ליעילותו המדהימה כזרז.
שינויים
שינויים אלה עשויים להיות אלקטרוניים עדינים, שינויים קוולנטיים משמעותיים יותר או שינויים מבניים הנובעים מהגמישות הגלומה באנזימים, אך אינם קיימים בזרזים כימיים. גמישות מאפשרת תנועה ותנועה מקלה על שינוי של סביבות אלקטרוניות הנחוצות לקטליזה. אנזימים, אם כן, יעילים בהרבה מזרזים כימיים קשיחים כתוצאה מיכולותיהם להקל על השינויים הדרושים לייעול התהליך הקטליטי.
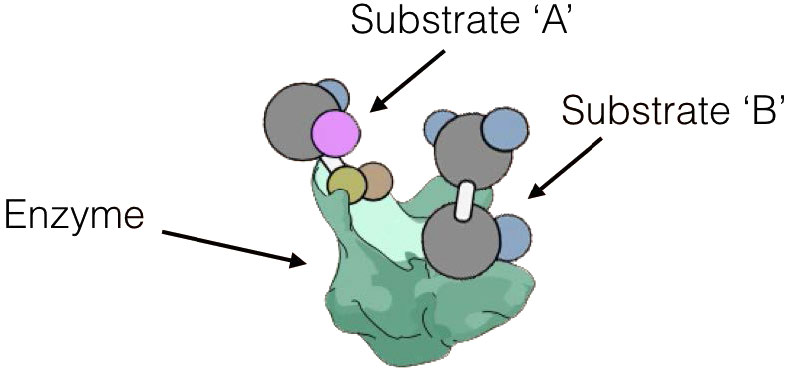
כריכת מצע
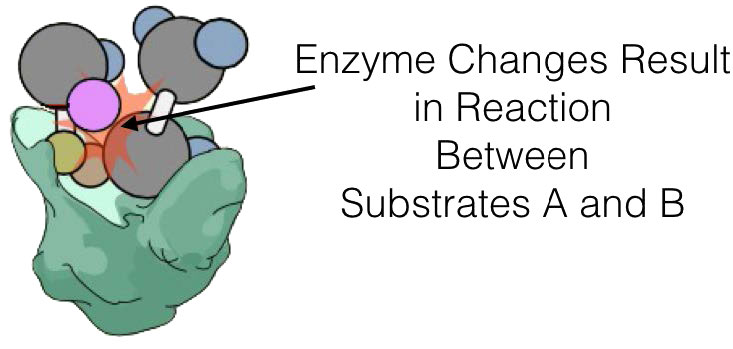
הבדל חשוב נוסף בין מנגנון הפעולה של אנזים לזרז כימי הוא שלאנזים יש אתרי קישור שלא רק 'תופסים' את המצע (מולקולה המעורבת בתגובה המזרזת), אלא גם ממקמים אותו במצב שבו ניתן לגרום אלקטרונית להגיב, בתוך עצמו או עם מצע אחר.
האנזים עצמו עשוי למלא תפקיד באינדוקציה האלקטרונית או שהאינדוקציה עלולה להתרחש כתוצאה מהצבת מצעים בסמיכות רבה זה לזה. לזרזים כימיים אין יכולת כזו לקשור מצעים והם תלויים בהתנגשותם בכיוון הנכון במשטחים שלהם או בקרבתם.
אתר פעיל
תגובות באנזים מזורזות במיקום ספציפי בתוכו המכונה 'האתר הפעיל'. מצעים נקשרים באתר הפעיל ומכוונים לספק גישה לחלק הרלוונטי של המולקולה לסביבה האלקטרונית של האנזים שבו מתרחשת קטליזה.
גמישות אנזים
כפי שהוזכר קודם לכן, ההבדל בין אנזים לזרז כימי הוא שאנזים גמיש. השינויים הקלים בצורתו (הנובעים לעתים קרובות מקשירת המצע עצמו) עוזרים למקם מצעים בצורה אופטימלית לתגובה לאחר שהם נקשרים.
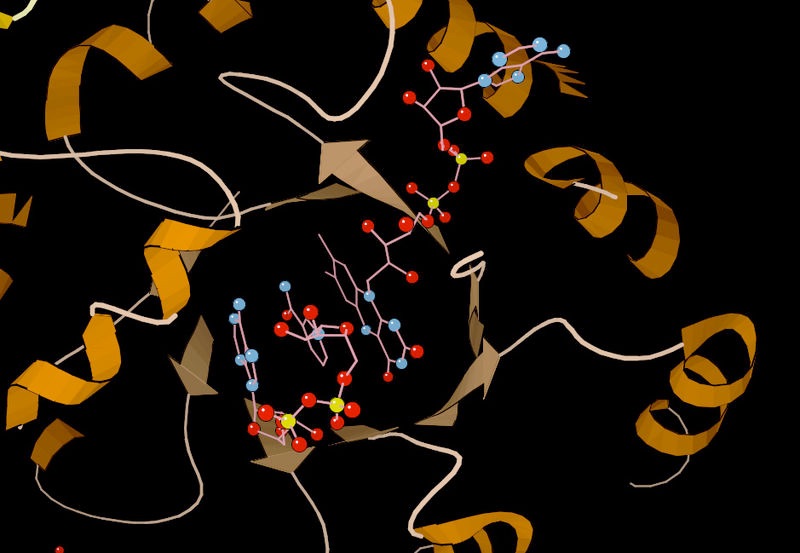
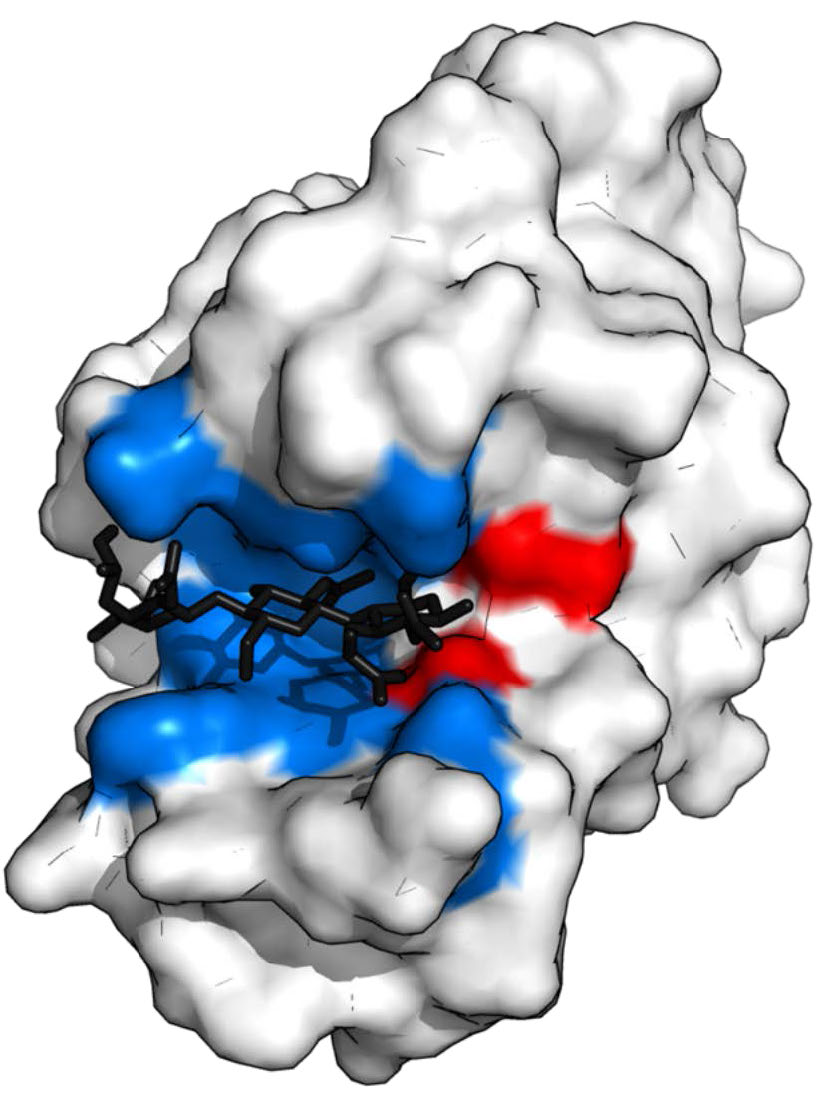
איור 4.5 - ליזוזים עם אתר מחייב מצע (כחול), אתר פעיל (אדום) ומצע קשור (שחור). ויקיפדיה
התאמה מושרה
שינויים אלה בצורתם מוסברים, בחלקם, על ידי מודל הקטליזה המושרה של קושלנד (איור 4.6), הממחיש כי לא רק אנזימים משנים מצעים, אלא שמצעים גם משנים באופן זמני את מבנה האנזים. בסוף הקטליזה, האנזים מוחזר למצבו המקורי. המודל של קושלנד עומד בניגוד למודל Fischer Lock and Key, שאומר בפשטות שלאנזים יש צורה קבועה המותאמת באופן מושלם לקשירת המצע (ים) שלו. גמישות האנזים חשובה גם לשליטה בפעילות האנזים. אנזימים מתחלפים בין מצב T (הדוק), שהוא מצב פעילות נמוך יותר למצב R (רגוע), בעל פעילות רבה יותר.
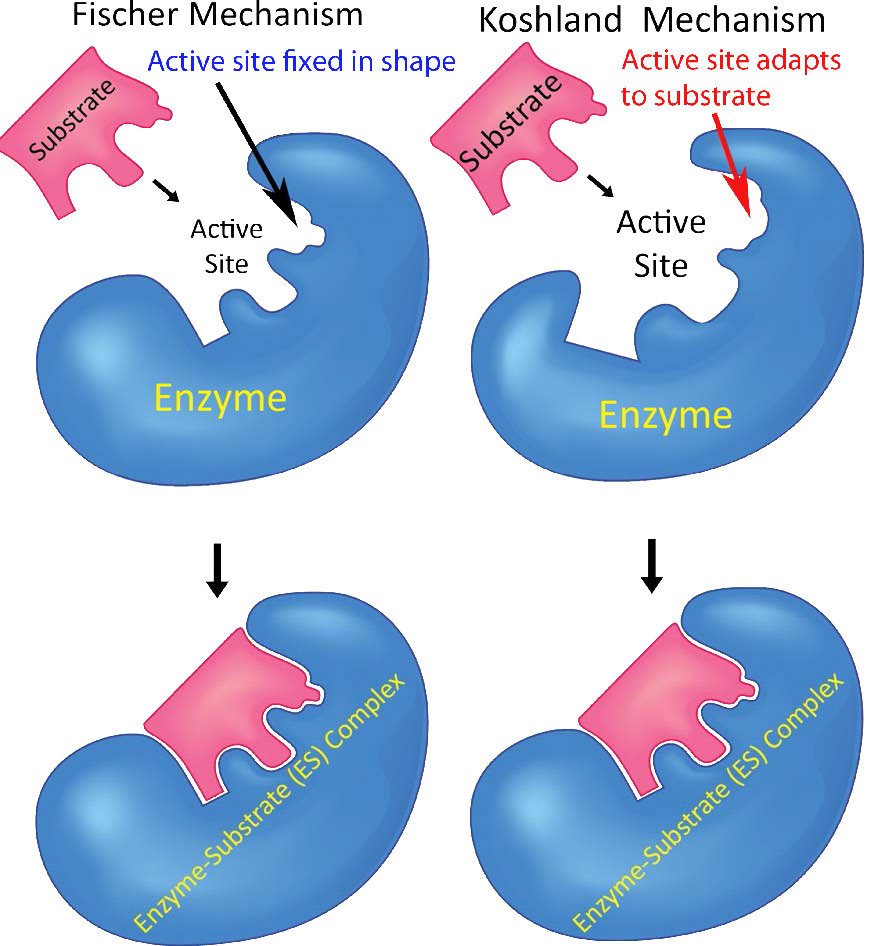
התאמה מושרה
מודל הקטליזה של Koshland Induced Fit מניח שאנזימים גמישים ומשנים צורה על מצע מחייב. שינויים בצורה עוזרים 1) לסייע בקשירה של מצעים נוספים בתגובות הכוללות יותר ממצע אחד ו/או 2) להקל על יצירת סביבה אלקטרונית באנזים המעדיפה קטליזה. מודל זה מנוגד למודל הקטליזה של פישר לוק והמפתח הרואה באנזימים אתרי קישור מצע שנוצרו מראש.
כריכה מסודרת
מודל קושלנד עולה בקנה אחד עם אנזימים קושרים מרובי סובסטרט המציגים קישור מסודר של מצעים. עבור מערכות אלו, קישור המצע הראשון גורם לשינויים מבניים באנזים הדרושים לקשירת המצע השני.
ישנן עדויות ניסיוניות ניכרות התומכות במודל קושלנד. הקסוקינאז, למשל, הוא אחד מאנזימים רבים הידועים כמי שעוברים שינוי מבני משמעותי לאחר קשירת המצע. במקרה זה, שני המצעים מובאים לקרבה מאוד על ידי ההתאמה המושרה והקטליזה מתאפשרת כתוצאה מכך.
סוגי תגובה
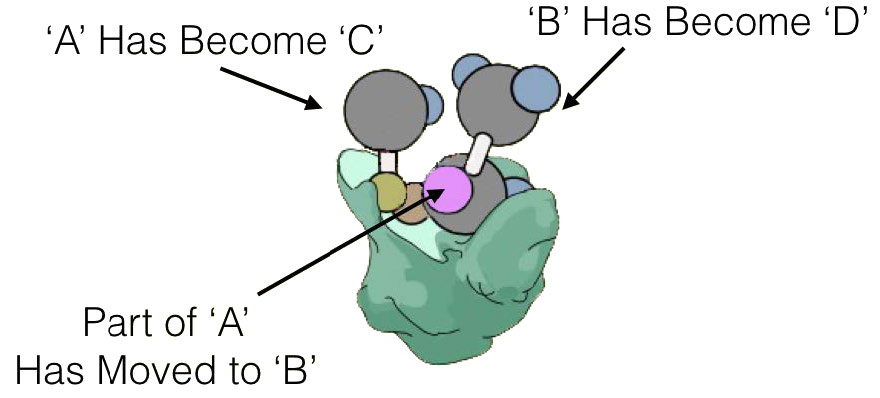
אנזימים המזרזים תגובות הכוללות יותר ממצע אחד, כגון
\[A + B \rightleftharpoons C + D\]
יכול לפעול בשתי דרכים שונות. תגובות אנזימטיות יכולות להיות מכמה סוגים, כפי שמוצג באיור 4.7. במנגנון אחד, הנקרא תגובות עוקבות, בשלב כלשהו בתגובה, שני המצעים יהיו קשורים לאנזים. יש, בתורו, שתי דרכים שונות שבהן זה יכול להתרחש - אקראי ומסודר.
| סוגי תגובות | |
|---|---|
| מצע יחיד - מוצר יחיד | א ב |
| מצע יחיד - מוצרים מרובים | א ב + ג |
| מצעים מרובים - מוצרים בודדים | א + ב ג |
| מצעים מרובים - מוצרים מרובים | א + ב ג + ד |
שקול לקטט דהידרוגנאז, המזרז את התגובה שלהלן:
\[NADH + Pyruvate → Lactate + NAD^+\]
אנזים זה דורש ש-NADH חייב להיקשר לפני הקישור של פירובט. כפי שצוין קודם לכן, זה עולה בקנה אחד עם מודל התאמה מושרה של קטליזה. במקרה זה, קישור ה- NADH משנה את צורה/הסביבה של האנזים כך שפירובט יכול להיקשר וללא קישור של NADH, המצע אינו יכול לגשת לאתר הקישור לפירובאט. סוג זה של תגובת מצע מרובה נקרא כריכה מסודרת רציפה, מכיוון שקשירת המצעים חייבת להתרחש בסדר הנכון כדי שהתגובה תמשיך.
כריכה אקראית
מנגנון שני של קשירה/קטליזה מוצג על ידי קריאטין קינאז המזרז את התגובה הבאה:
\[Creatine + ATP → \text{Creatine phosphate} + ADP\]
עבור אנזים זה, מצעים יכולים להיקשר אליו בכל סדר. קריאטין קינאז מציג כריכה אקראית רציפה. ראוי להזכיר כי כריכה אקראית אינה עולה בקנה אחד עם מודל ההתאמה המושרה של קושלנד. במקום זאת, קישור אקראי פשוט אומר שההתאמה המושרה של האנזים אינה משפיעה על אתרי קישור המצע וכוללת חלקים אחרים של האנזים. לסיכום, כריכה רציפה יכולה להתרחש ככריכה מסודרת או ככריכה אקראית.
תגובות עקירה כפולות
עם זאת, לא כל האנזימים המזרזים תגובות מרובות סובסטרט, קושרים את A ו-B על ידי המנגנונים העוקבים שלמעלה. קטגוריה אחרת זו של אנזים כוללת את אלה המציגים את מה שמכונה מנגנוני "פינג-פונג" (או תזוזה כפולה). באנזימים אלו האנזים מתפקד הן כזרז והן כנשא של קבוצה בין מצעים הקשורים בנפרד. דוגמאות לסוג זה של אנזים כוללות את סוג האנזימים המכונה טרנסמינזות. צורה כללית של התגובות המזרזות על ידי אנזימים אלה מוצגת באיור 4.8.
בתגובות טרנסמינאז הפיכות, חמצן ואמין מתחלפים בין המולקולות. ניתן לייצג אותו באופן הבא (כאשר N הוא האמין ו- O הוא החמצן).
A=O + C = N B-N + ד=O
תגובה זו מתרחשת לא כתגובת העברה אחת המחליפה את ה- N וה- O, אלא כקבוצה של שתי תגובות חצי. במקרה זה, האנזים הוא תורם וגם נשא של הקבוצה המוחלפת. חצי התגובה הראשונה הולכת כדלקמן
A = O + אנץ-נ ב-נ+אנז=O
לאחר מכן חצי תגובה שנייה הולכת כמו
C-N + אנז=O ד=או+אנז=נ
סכום חצאי התגובות הללו הוא אז
A=O + C = N B-N + ד=O
שימו לב שבשום זמן לא נקשר האנזים גם A וגם C בו זמנית. חשוב גם להכיר בכך שהאנזים היה קיים בשני מצבים - Enz = O ו- Enz-N. דשדוש האנזים בין שני המצבים הללו הוא מה שמוליד את שם הפינג-פונג של המנגנון הזה - הוא ממש הולך קדימה ואחורה כמו כדור פינג-פונג במשחק טניס שולחן.
קינטיקה של אנזים
כדי להבין כיצד אנזים משפר את קצב התגובה, עלינו להבין את קינטיקה של האנזים. אנו מציגים כאן מודל שהוצע על ידי ליאונור מיכאליס ומוד מנטן. כדי להבין את המודל, יש צורך להבין כמה פרמטרים.
ראשית, אנו מתארים תגובה במונחים פשוטים המתנהלת כדלקמן
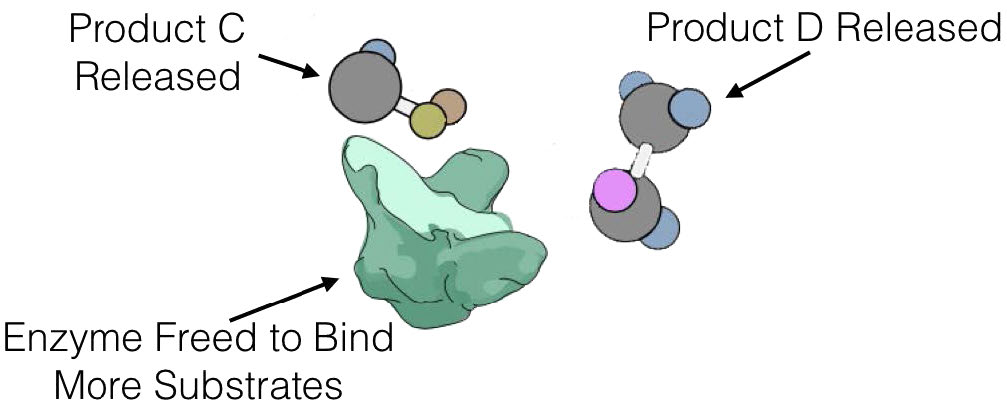
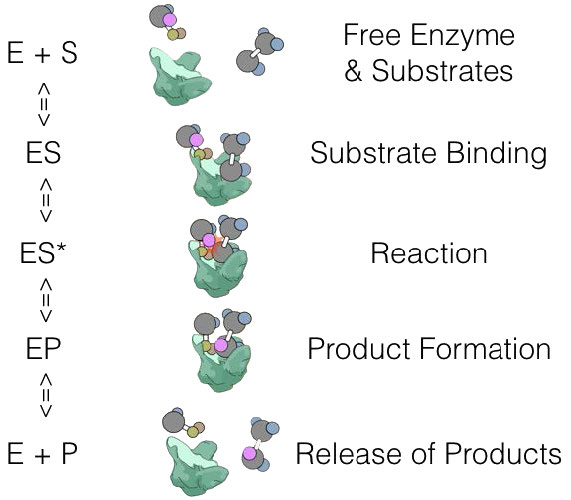
E + S ES -> E + P
כאשר E הוא אנזים, S הוא מצע ו- P הוא תוצר. בתכנית זו, ES הוא קומפלקס האנזים-מצע, שהוא פשוט האנזים הקשור למצע שלו.
נוכל להגדיר את מצב ES קצת יותר עם
E + S ES -> ES* -> EP -> E + P
כאשר ES* הוא המצב המופעל ו- EP הוא קומפלקס מוצר האנזים לפני שחרור המוצר.
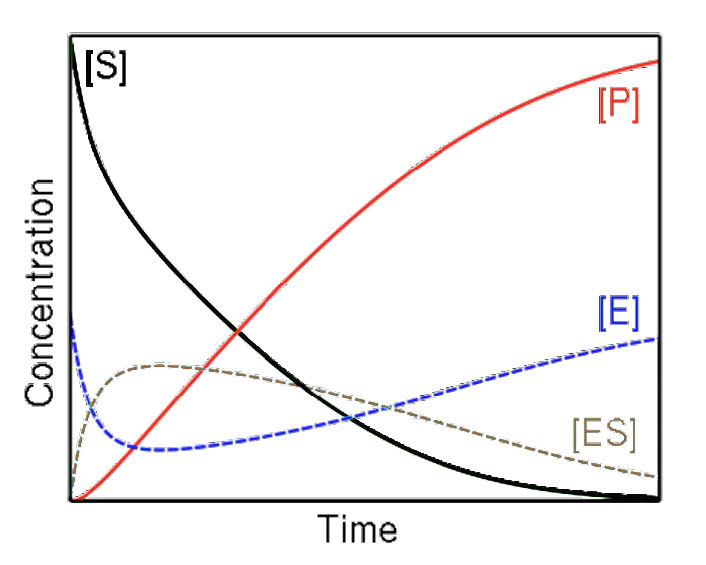
השיקול הראשון שיש לנו הוא מהירות. מהירות התגובה היא קצב יצירת המוצר לאורך זמן, הנמדד כריכוז המוצר בכל פעם. הזמן הוא שיקול קריטי בעת מדידת המהירות. במערכת סגורה (שבה פועל אנזים), כל התגובות יתקדמו לעבר שיווי משקל. תגובות מזורזות אנזימטית אינן שונות בתוצאה הסופית מתגובות לא אנזימטיות, אלא שהן מגיעות לשיווי משקל מהר יותר.
שיווי משקל
בשיווי משקל, היחס בין מוצר למגיב אינו משתנה. זה מאפיין של שיווי משקל. מכיוון שהמערכת סגורה, ריכוז המוצר לאורך זמן לא ישתנה. המהירות תהיה אפוא אפס בתנאים אלה ולא נלמד דבר על התגובה אם נחכה יותר מדי זמן ללמוד אותה.
מהירות
כתוצאה מכך, בקינטיקה של מיכאליס-מנטן, המהירות נמדדת כמהירות התחלתית (V0). זה מושג על ידי מדידת קצב היווצרות המוצר בשלב מוקדם של התגובה לפני קביעת שיווי המשקל ובתנאים אלה, יש מעט מאוד אם בכלל מהתגובה ההפוכה המתרחשת.
שתי ההנחות האחרות קשורות זו לזו. ראשית, אנו משתמשים בתנאים שבהם יש הרבה יותר מצע מאשר אנזים. זה הגיוני. אם המצע אינו בעודף גדול, אז ההמרה של האנזים של המצע למוצר תתרחש הרבה יותר מהר ממה שהאנזים יכול לקשור מצע.
מחכה למצע
לפיכך, האנזים "יחכה" למצע להיקשר אם לא היו כמויות מספיקות שלו כדי להיקשר לאנזים בזמן (כאשר ריכוז המצע נמוך). זה לא ייתן מדד מדויק של מהירות, מכיוון שהאנזים לא יהיה פעיל חלק ניכר מהזמן. בגלל זה, אנו מניחים שרוויה של האנזים במצע תיתן מהירות מקסימלית של התגובה.
מצב יציב
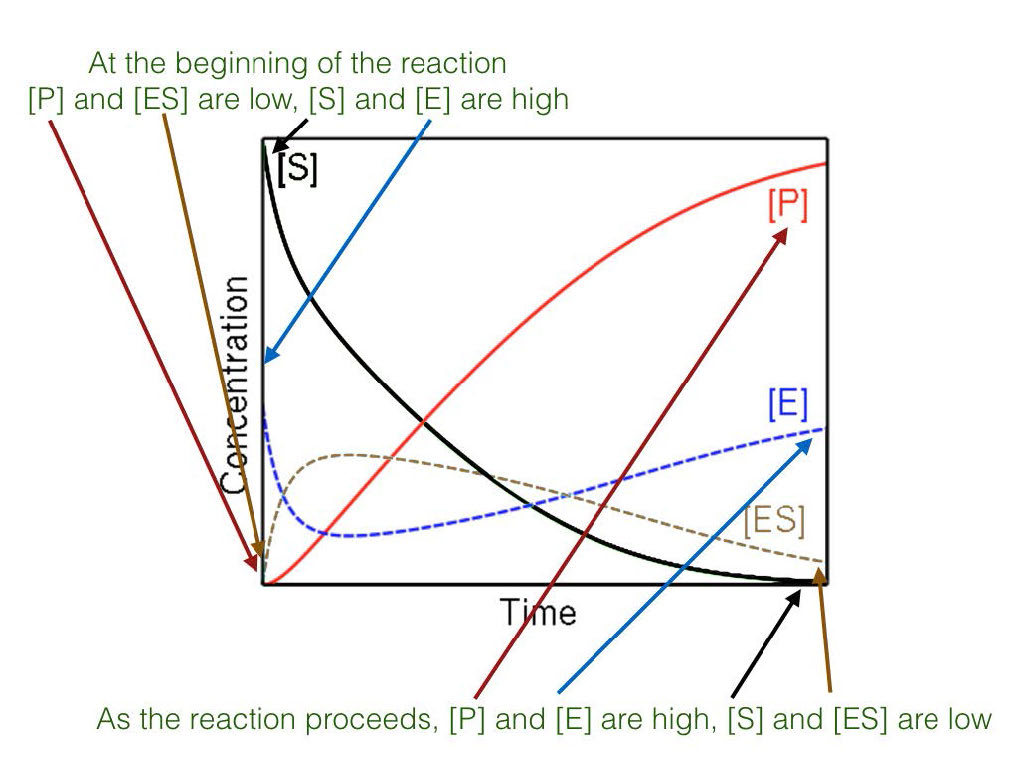
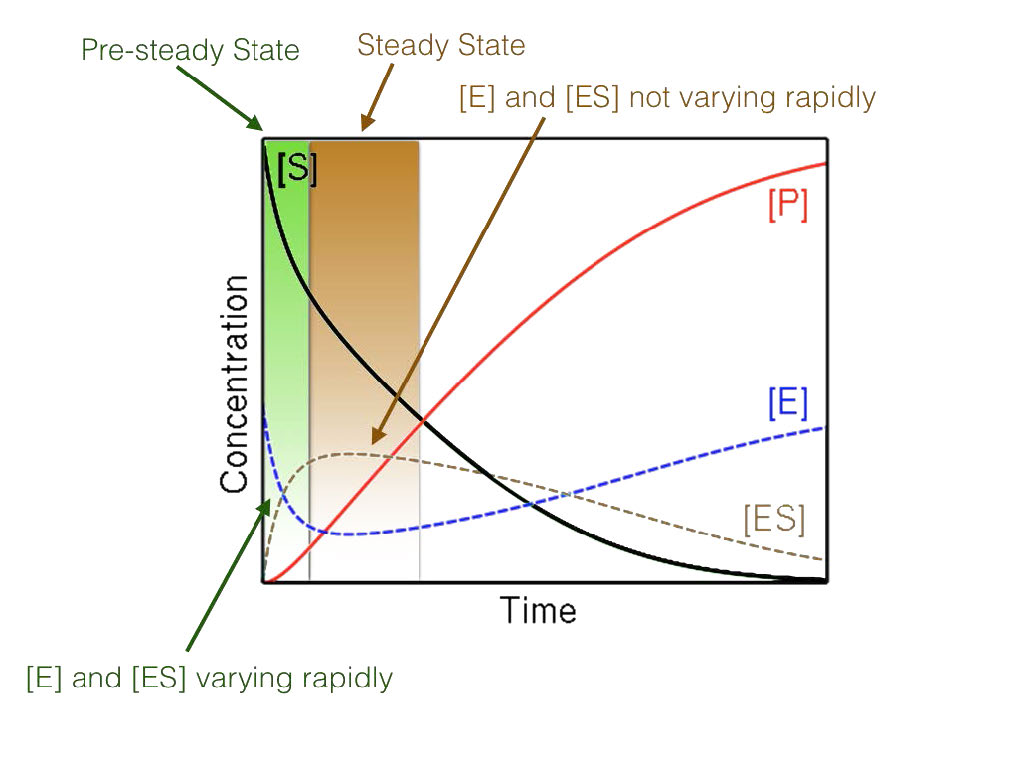
איור 4.17 - מצב יציב לעומת תנאי מצב לא יציב
לבסוף, הריכוז הגבוה של המצע בשילוב עם מדידת תנאים ראשוניים מביא לחקר תגובות שנמצאות בתנאי מצב יציב כביכול (איור 4.17). כאשר מתרחש מצב יציב, הריכוז של קומפלקס ES לאורך זמן אינו משתנה באופן משמעותי במהלך תקופת הניתוח.
חוזר ומדגיש, שלוש ההנחות לקינטיקה של מיכאליס-מנטן הן
- מדידת המהירות ההתחלתית של תגובה
- מצע בעודף רב בהשוואה לאנזים
- תנאי תגובה המתרחשים במצב יציב
שיקולים ניסיוניים
כעת אנו מפנים את תשומת ליבנו לאופן בו נערכים מחקרים על התכונות הקינטיות של אנזים. כדי לבצע ניתוח, אפשר היה לעשות את הניסוי הבא - 20 צינורות שונים יוקמו עם מאגר אנזים (כדי לשמור על יציבות האנזים), אותה כמות אנזים, ולאחר מכן כמות שונה של מצע בכל צינור, החל מזעיר כמויות בצינורות הראשונים לכמויות גדולות מאוד בצינורות האחרונים. התגובה תתאפשר להמשיך לפרק זמן קבוע וקצר ואז התגובה תיעצר ותיקבע כמות המוצר הכלולה בכל צינור.
המהירות ההתחלתית (V0) של התגובה אז תהיה ריכוז המוצר שנמצא בכל צינור חלקי הזמן שהתגובה הורשה לפעול. נתונים מהניסוי יתווטו על גרף באמצעות מהירות התחלתית (V0) על ציר Y וריכוז המצע על ציר ה- X, לכל צינור, כמובן שיש מהירות תגובה ייחודית המתאימה לריכוז מצע ייחודי.
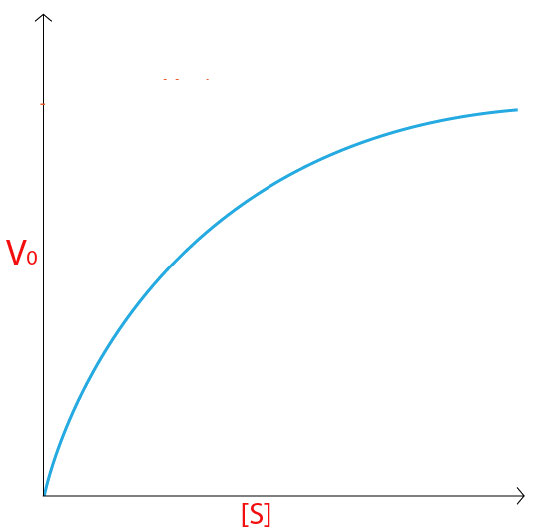
עבור אנזים העוקב אחר קינטיקה של מיכאליס-מנטן, תיווצר עקומה כמו זו המוצגת באיור 4.18 או 4.19. בריכוז נמוך של מצע, הוא מגביל והאנזים ממיר אותו למוצר ברגע שהוא יכול לקשור אותו. כתוצאה מכך, בריכוזים נמוכים של מצע, קצב העלייה של [P] כמעט ליניארי עם [S] (איור 4.19).
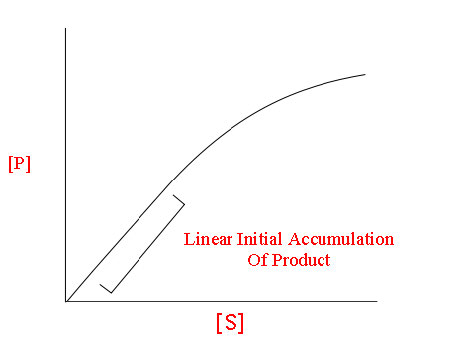
איור 4.19 - קשר לינארי בין [P] ו- [S] ב- [S] נמוך
עלייה לא ליניארית
עם זאת, ככל שריכוז המצע עולה, מהירות התגובה בצינורות עם ריכוז מצע גבוה יותר מפסיקה לעלות באופן ליניארי ובמקום זאת מתחילה להשתטח החוצה, מה שמצביע על כך שככל שריכוז הסובסטרט עולה יותר ויותר, לאנזים קשה יותר לעמוד בקצב להמיר את המצע למוצר.
רוויה
באופן לא מפתיע, כאשר האנזים הופך רווי לחלוטין במצע, הוא לא יצטרך לחכות למצע שיתפזר אליו ולכן יפעל במהירות מרבית.
עבור אנזים העוקב אחר קינטיקה של מיכאליס-מנטן תהיה מהירותו (v) בכל ריכוז מצע נתון שניתן על ידי המשוואה הבאה:
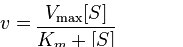
מקסימום V
שני מונחים במשוואה לעיל דורשים הסבר. הראשון הוא V max. זה מתייחס למהירות המרבית של תגובה אנזימטית. מהירות מרבית לתגובה מתרחשת כאשר אנזים רווי במצע. הרוויה חשובה מכיוון שמשמעותה (לפי ההנחה לעיל) שאף אחת ממולקולות האנזים לא "ממתינה" למצע לאחר שחרור המוצר. הרוויה מבטיחה שמצע אחר יהיה זמין תמיד באופן מיידי. היחידה של V max היא ריכוז המוצר לכל זמן = [P] /זמן.
בעלילה של מהירות התחלתית לעומת ריכוז המצע (V0 לעומת [S]), V max הוא הערך על ציר Y אליו העקומה מתקרבת באופן אסימפטוטי (קו מקווקו באיור 4.20). יש לציין כי הערך של V max תלוי בכמות האנזים המשמשת בתגובה. אם תכפיל את כמות האנזים בשימוש, תכפיל את ה-V max. אם רוצים להשוות את המהירויות של שני אנזימים שונים, יהיה צורך להשתמש באותן כמויות של אנזים בתגובה שכל אחד מזרז.
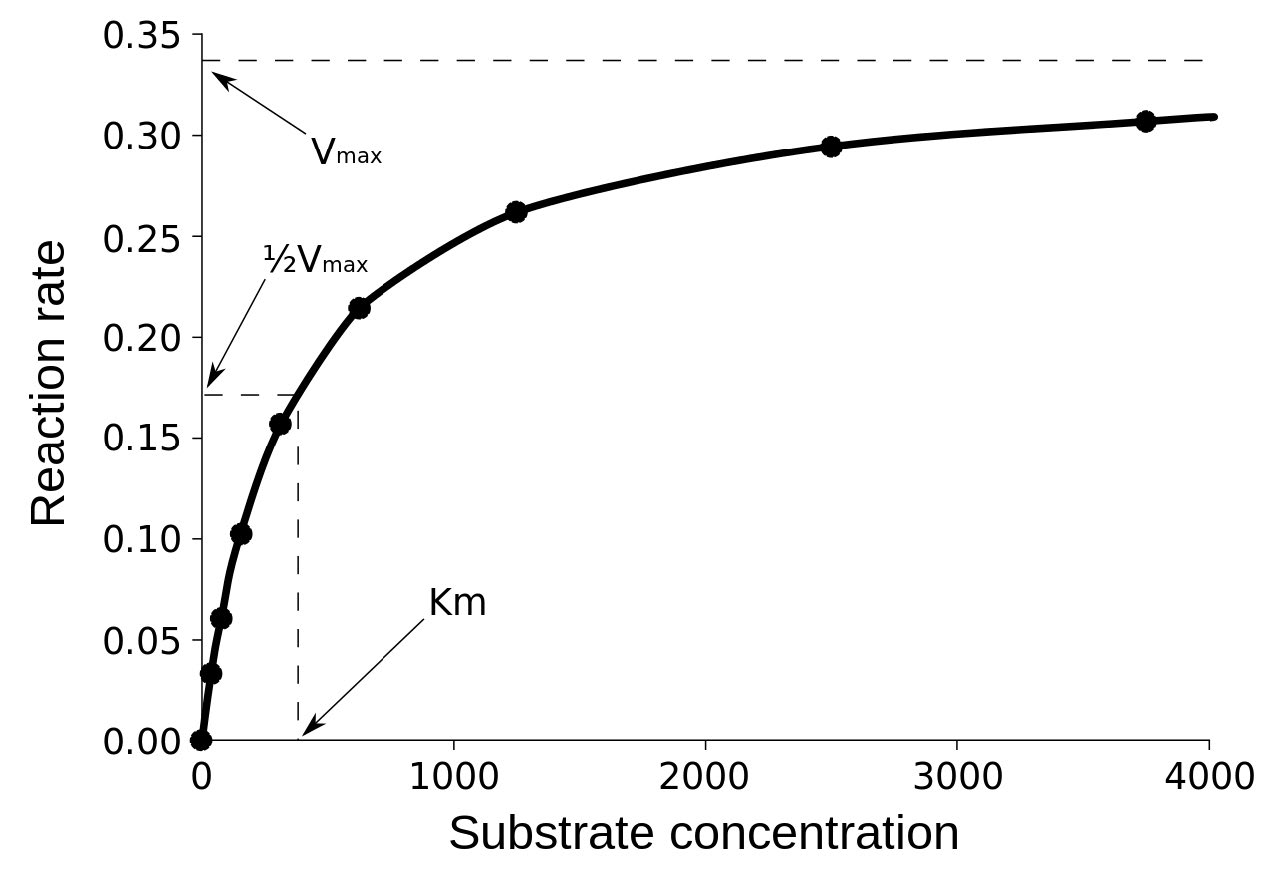
Km
המונח השני הוא Km (הידוע גם בשם Ks). המכונה קבוע מיכאליס, קM הוא ריכוז המצע שגורם לאנזים לעבוד במחצית מהמהירות המרבית (Vmax/2). מה שהוא מודד, במילים פשוטות, הוא הזיקה שיש לאנזים למצע שלו. הערך של Km קשור הפוך לזיקה של האנזים למצע שלו. לאנזימים בעלי ערך Km גבוה תהיה זיקה נמוכה יותר למצע שלהם (ייקח יותר מצע כדי להגיע ל-Vmax/2) בעוד שלבעלי Km נמוך תהיה זיקה גבוהה וייקח פחות מצע כדי להגיע ל-Vmax/2. יחידת Km היא ריכוז.
הזיקה של אנזימים לסובסטרטים משתנה במידה ניכרת, כך שידיעת Km עוזרת לנו להבין עד כמה אנזים מתאים למצע הנמצא בשימוש. מדידת Km תלויה במדידת Vmax.
טעות נפוצה
טעות נפוצה שתלמידים עושים בתיאור Vmax היא לומר ש- Km = Vmax /2. זה, כמובן, לא נכון. Km הוא ריכוז מצע והוא כמות המצע שלוקח לאנזים להגיע ל-Vmax /2. מצד שני Vmax /2 הוא מהירות ומהירות בהחלט לא יכולה להיות שווה לריכוז.
קקאט
רצוי שיהיה מדד מהירות שאינו תלוי בריכוז האנזים. זכור כי Vmax תלוי בכמות האנזים בשימוש. לשם כך אנו משתמשים ב- Kcat, המכונה גם מספר המחזור. Kcat הוא מספר הדורש אחד לקבוע תחילה Vmax עבור אנזים ולאחר מכן לחלק את Vmax בריכוז האנזים המשמש לקביעת Vmax. לפיכך,
Kcat = Vmax/[אנזים]
מכיוון של- Vmax יש יחידות ריכוז בכל פעם ול- [לאנזים] יש יחידות ריכוז, היחידות ב- Kcat הן זמן-1. למרות שזה אולי נראה לא אינטואיטיבי, זה אומר שהערך של Kcat הוא מספר מולקולות המוצר שנוצרו על ידי כל מולקולת אנזים בזמן הנתון. אז, ערך Kcat של 1000/sec פירושו שכל מולקולת אנזים בתגובה ב-Vmax מייצרת 1000 מולקולות של מוצר בשנייה. שים לב שמכיוון ש- Kcat הוא ערך מחושב, לא ניתן לקרוא אותו מגרף V לעומת [S] כפי ש- Vmax ו- Km יכולים.

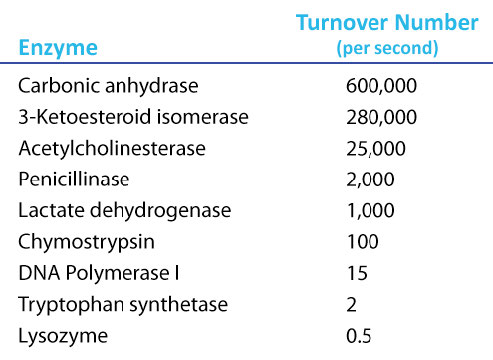
ערכי Kcat מדהימים
ערך Kcat של 1000 מולקולות של מוצר לאנזים לשנייה עשוי להיראות כמו ערך גבוה, אך ישנם אנזימים ידועים (פחמן אנהידראז, למשל) בעלי ערך Kcat של מעל 600,000/שנייה (איור 4.21). ערך מדהים זה ממחיש בבירור מדוע אנזימים נראים כמעט קסומים בפעולתם. בניגוד ל\(V_{max}\), המשתנה עם כמות האנזים בשימוש, Kcat הוא קבוע לאנזים בתנאים נתונים.
כפי שנראה קודם לכן, אנזימים העוקבים אחר קינטיקה של מיכאליס-מנטן מייצרים עלילות היפרבוליות של מהירות (V0) לעומת ריכוז מצע [S] (איור 4.18). עם זאת, לא כל האנזימים עוקבים אחר הקינטיקה של מיכאליס-מנטן. לאנזימים רבים יש תת-יחידות חלבון מרובות ולעיתים אלה מתקיימות באופן שונה עם קישור של מצע או מולקולה חיצונית. ראה בCase (כאן) לדוגמא.
אנזימים מושלמים
עכשיו, אם נחשוב מה יכול להיות אנזים אידיאלי, זה יהיה כזה שיש לו מהירות גבוהה מאוד וזיקה גבוהה מאוד למצע שלו. כלומר, לא יידרש הרבה מצע כדי להגיע ל- Vmax/2 וה- Kcat יהיה גבוה מאוד. לאנזימים כאלה יהיו ערכים של Kcat/Km שהם מקסימליים. מעניין לציין כי ישנם מספר אנזימים בעלי תכונה זו וערכי Kcat/Km המקסימליים שלהם כולם זהים בערך. אנזימים כאלה מכונים "מושלמים" מכיוון שהם הגיעו לערך המרבי האפשרי.
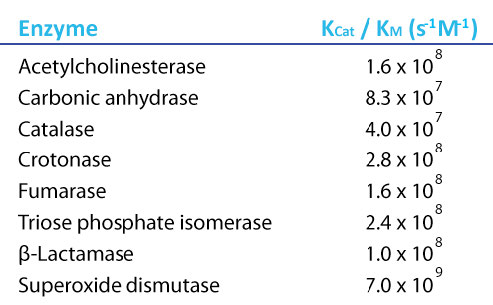
איור 4.22 - ערכי Kcat/Km לאנזימים מושלמים. תמונה על ידי אליה קים


הגבלת דיפוזיה
מדוע צריך להיות ערך מקסימלי אפשרי של Kcat/Km? התשובה היא שתנועת המצע לאנזים הופכת לגורם המגביל לאנזימים מושלמים. לתנועת המצע על ידי דיפוזיה במים יש קצב קבוע בכל טמפרטורה ומגבלה זו קובעת בסופו של דבר את המהירות המרבית בה יכול אנזים לזרז. באנלוגיה עולמית מקרוסקופית, מפעלים לא יכולים לייצר מוצרים מהר יותר ממה שספקים יכולים לספק חומרים. זה בטוח לומר עבור אנזים מושלם שמגבלת המהירות היחידה שיש לו היא קצב דיפוזיה המצע במים.
בהתחשב ב"קסם "האנזימים שנרמז קודם לכן, נראה כי כל האנזימים היו צריכים להתפתח להיות" מושלמים". יש סיבות טובות מאוד לכך שרובם לא עשו זאת.
מהירות
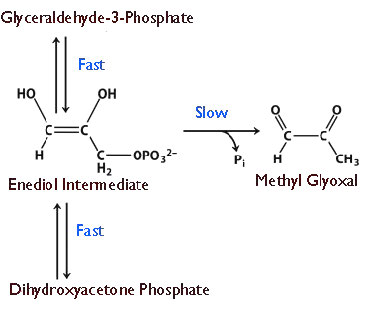
מהירות היא דבר מסוכן. ככל שתגובה מתקדמת מהר יותר בקטליזה על ידי אנזים, כך קשה יותר לשלוט בה. כפי שכולנו יודעים מלימוד נהיגה, מהירות מופרזת גורמת לתאונות. בדיוק כפי שנהגים צריכים להיות בעלי מגבלות מהירות להפעלת מכוניות, כך גם התאים חייבים להפעיל שליטה מסוימת על 'המצערת' של האנזימים שלהם. לאור זאת, אפשר לתהות אז מדוע תאים כלשהם פיתחו אנזימים כלשהם לשלמות. אין תשובה אחת לשאלה, אך תשובה נפוצה מודגמת על ידי איזומראז פוספט טריוז, המזרז תגובה בגליקוליזה המוצגת באיור 4.24.
נראה שהאנזים פיתח יכולת זו מכיוון שבמהירויות נמוכות יותר, יש פירוק של תוצר ביניים אנדיול לא יציב שיוצר אז בקלות מתיל גליוקסל, תרכובת ציטוטוקסית (איור 4.25). האצת התגובה מספקת פחות הזדמנות לתווך הבלתי יציב להצטבר ופחות תוצרי לוואי לא רצויים.
קבוע דיסוציאציה
בחקר חלבונים וליגנדים, חשוב להבין את ה"אטימות" שבה חלבון (P) "אוחז" בליגנד (L). זה נמדד עם קבוע הדיסוציאציה (\(K_d\)). היווצרות קומפלקס ליגנד-חלבון מתרחשת כ \(LP\)
\[L + P \rightleftharpoons LP\]
הדיסוציאציה של המתחם, אם כן, היא ההפך מתגובה זו, או
\[LP \rightleftharpoons L + P\]
כך שקבוע הדיסוציאציה המקביל מוגדר כ
\[K_d = \dfrac{[L][P]}{[LP]}\]
היכן\([L]\),\([P]\), \([LP]\) והם הריכוזים הטוחניים של החלבון, הליגנד והמתחם כאשר הם מחוברים זה לזה.
ערכים קטנים יותר של \(K_d\) מצביעים על כריכה הדוקה, בעוד שערכים גדולים יותר מצביעים על כריכה רופפת. קבוע הדיסוציאציה הוא ההיפוך של קבוע האסוציאציה.
\[K_a = \dfrac{1}{K_d}\]
כאשר מולקולות מרובות נקשרות זו לזו, כגון
\[J_xK_y \rightleftharpoons xJ + yK\]
המתחם \(J_xK_y\) מתפרק ליחידות \(x\) משנה של \(J\) \(y\) ויחידות משנה של. \(K\) קבוע הדיסוציאציה מוגדר אז כ
\[K_d = \dfrac{[J]^x[K]^y}{[J_xK_y]}\]
איפה\([J]\),\([K]\), \([J_xK_y]\) והם הריכוזים של J, K והמתחם\(J_xK_y\), בהתאמה.
חלקות ליינווייבר-בורק
חקר קינטיקה של האנזים הוא בדרך כלל המרכיב האינטנסיבי ביותר במתמטיקה בביוכימיה ואחד ההיבטים המרתיעים ביותר של הנושא עבור תלמידים רבים. למרות שנעשים ניסיונות לפשט את השיקולים המתמטיים, לפעמים הם משמשים רק לבלבל או לתסכל תלמידים. כזה הוא המקרה עם חלקות אנזים שהשתנו, כגון Lineweaver-Burk (איור 4.26).
ואכן, כאשר מוצגים על ידי פרופסורים כדבר נוסף שיש לשנן, מי יכול להאשים את התלמידים? במציאות, שתי המגרשים הללו נועדו לפשט את קביעת הפרמטרים, כגון \(K_m\) ו\(V_{max}\). ביצירת אחת מהעלילות המתוקנות הללו, חשוב להכיר בכך שמשתמשים באותם נתונים כמו ביצירת עלילת V0 לעומת [S]. הנתונים פשוט מנוהלים כדי להקל על העלילה.
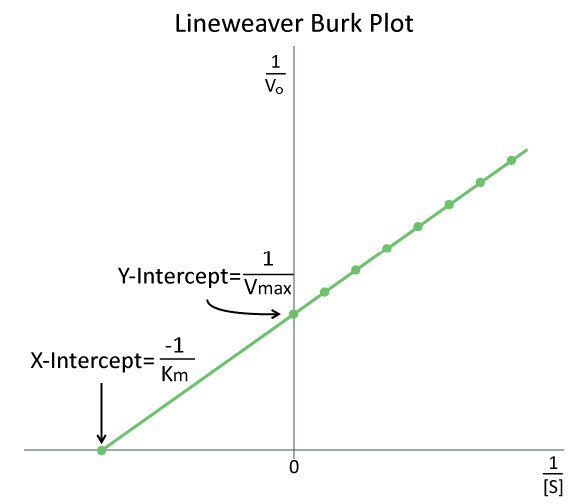
איור 4.26 - עלילת ליינוויבר-בורק של vs. \(1/V_0\) \(1/[S]\) תמונה על ידי אליה קים
הדדי כפול
עבור עלילת LineWeaver-Burk, המניפולציה משתמשת בהדדיות של הערכים הן של המהירות והן של ריכוז המצע. הערכים ההפוכים מתווים לאחר מכן בגרף כ- 1/V0 לעומת 1/ [S]. בגלל היפוכים אלה, מגרשים Lineweaver-Burk מכונים בדרך כלל חלקות 'הדדיות כפולה'. כפי שניתן לראות באיור 4.26, הערך של Km על עלילת Lineweaver Burk נקבע בקלות כהדדיות השלילית של יירוט ה- x, ואילו ה- Vmax הוא ההיפוך של יירוט ה- y. מניפולציה קשורה אחרת של נתונים קינטיים כוללת דיאגרמות Eadie-Hofstee, המתווה V0 לעומת V0/ [S] ונותן Vmax כציר Y יירוט כאשר שיפוע הקו הוא -Km.
מולקולריות של תגובות
המונח מולקולריות מתייחס למספר המולקולות שחייבות להתאחד על מנת שתתרחש תגובה. תגובות מסוג A -> B (כאשר 'A' הוא המגיב ו- 'B' הוא המוצר) הן חד-מולקולריות, שכן A משתנה ישירות ל-B. קצב התגובה קשור רק לריכוז המגיב A. לתגובה דו-מולקולרית שבה A + B C התגובה תלויה בריכוז של A ו-B והקצב שלה יהיה קשור לתוצר של ריכוז A ו-של A ושל B.
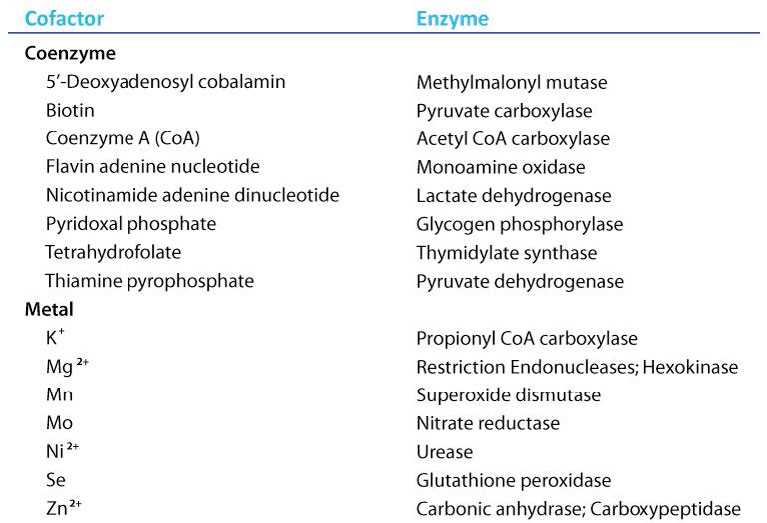
קואנזימים
מולקולות אורגניות המסייעות לאנזימים ומקלות על קטליזה הן גורמים משותפים הנקראים קו-אנזימים. המונח קו-פקטור הוא קטגוריה רחבה המחולקת בדרך כלל ליונים אנאורגניים וקו-אנזימים. אם הקואנזים קשור בצורה הדוקה מאוד או קוולנטית לאנזים, הוא מכונה קבוצה תותבת. אנזימים ללא הגורמים המשותפים שלהם אינם פעילים ומכונים אפואנזימים. אנזימים המכילים את כל הגורמים המשותפים שלהם נקראים הולואנזימים.
מחקרים קינטיים במצב יציב מראש
בחקר השיעורים הקינטיים של תגובות אנזימטיות, זמן אפס הוא נקודה קריטית מאוד. זה קובע מתי מתחיל ערבוב המצע עם האנזים ומדידת היווצרות המוצר. בזמן אפס, אין מוצר. כפי שמוצג באיור 4.29, מראה המוצר (בסולם זמן קצר) עובר שלב פרץ מוקדם עם שיפוע תלול עבור [מוצר] /זמן ולאחר מכן משתנה.
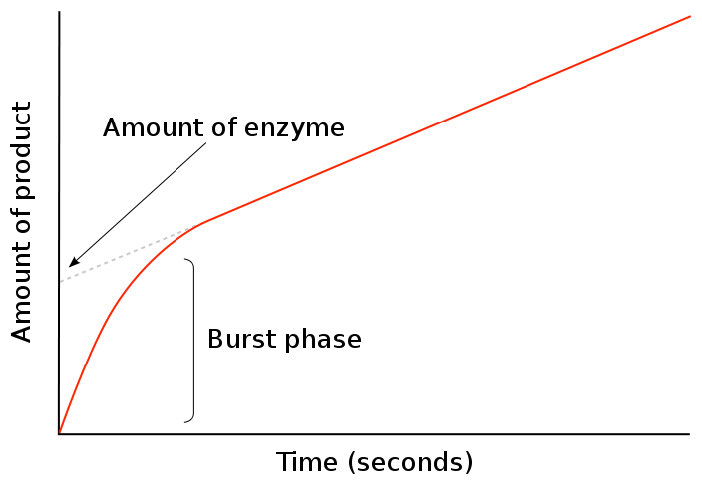
איור 4.29 - שלב פרץ של היווצרות המוצר
שינוי זה מתרחש בתקופה קריטית בתגובה אנזימטית ונותן מידע על קצב מחזורי התגובה. משך שלב ההתפרצות מספר כמה זמן מתרחשת מחזור תגובה בודד, ואילו השלב האיטי של הקו שלאחר הפיצוץ מספר את כמות האנזים ה"פונקציונלי" המבצע את התגובה.
לאחר שלב ההתפרצות, שיפוע הקו של כמות המוצר לעומת הזמן פוחת. הסיבה לכך היא התגובה הנכנסת לתנאים של מצב יציב, המשמשת לחקר קינטיקה של מיכאליס-מנטן. בתנאי מצב יציב, כמות קומפלקס האנזים-סובסטרט (ES) קבועה יחסית לאורך זמן. במילים פשוטות, זה קורה כאשר קצב היווצרות קומפלקס ES שווה לקצב ההמרה של המצע למוצר על ידי האנזים עם שחרור המוצר.
אירועים קודמים
אירועים המתרחשים לפני תנאי המצב היציב מכונים מצב טרום יציב. בהתאם לאנזים, תוך כמה אלפיות השנייה, יכולים להיות תנאי מצב יציב כלומר אם מקווים ללמוד היווצרות של תוצרי ביניים לתגובה במצב טרום יציב, כלים לניתוח זה חייבים לעבוד מהר מאוד. מכשיר אחד המשמש בדרך כלל לחקר קינטיקה של מצב יציב נקרא מכשיר זרימה עצורה.
הוא טוען תמיסת אנזים ומצע למזרקים נפרדים שתפוקתם מכוונת לתא ערבוב. הפתרונות מעורבבים במהירות ומתחילות מדידות ריכוז המוצר. בעזרת מכשיר זרימה עצור, ניתן להשיג זמנים מתים (זמן בין ערבוב לגילוי) של עד 0.3 אלפיות השנייה.

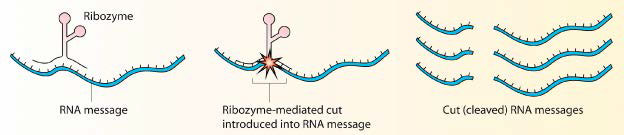
ריבוזימים
לחלבונים אין מונופול על פעולה כזרזים ביולוגיים. חלק ממולקולות ה- RNA מסוגלות גם להאיץ תגובות. המפורסמת מבין המולקולות הללו התגלתה על ידי טום צ'ך בתחילת שנות השמונים בחקר כריתה של אינטרון בטטרהימנה, צ'ך תהה מחוסר יכולתו למצוא חלבונים המזרזים את התהליך. בסופו של דבר, הקטליזה הוכרה כמגיעה מהאינטרון עצמו. זה היה RNA שחבור עצמי ומאז נמצאו דוגמאות רבות אחרות של RNA קטליטי. מולקולות RNA קטליטיות ידועות בשם ריבוזימים.
 359
359
לא יוצא דופן
ריבוזימים, לעומת זאת, אינם נדירים בטבע. הריבוזומים המייצרים חלבון של תאים הם בעצם ריבוזימים ענקיים. ה-23S rRNA של הריבוזום הפרוקריוטי וה-28S rRNA של הריבוזום האוקריוטי מזרזים את היווצרותם של קשרי פפטיד.
ריבוזימים חשובים גם בהבנתנו את התפתחות החיים על פני כדור הארץ. הוכח שהם מסוגלים באמצעות בחירה לפתח שכפול עצמי. ואכן, ריבוזימים למעשה עונים על דילמת עוף/ביצה - שהגיעה ראשונה, אנזימים שעושים את עבודת התא או חומצות גרעין הנושאות את המידע הנדרש לייצור האנזימים. כנשאים של מידע גנטי וזרזים כאחד, ריבוזימים הם ככל הנראה גם העוף וגם הביצה במקור החיים.


