5.1: مرونة سعر الطلب ومرونة سعر العرض
- Last updated
- Save as PDF
- Page ID
- 212218
يوضح كل من منحنى الطلب والعرض العلاقة بين السعر وعدد الوحدات المطلوبة أو الموردة. مرونة السعر هي النسبة بين النسبة المئوية للتغير في الكمية المطلوبة (Qd) أو الموردة (Qs) والنسبة المئوية المقابلة للتغير في السعر. مرونة سعر الطلب هي النسبة المئوية للتغير في الكمية المطلوبة من السلعة أو الخدمة مقسومًا على النسبة المئوية للتغير في السعر. مرونة سعر العرض هي النسبة المئوية للتغير في الكمية الموردة مقسومًا على النسبة المئوية للتغير في السعر.
يمكن تقسيم المرونة بشكل مفيد إلى ثلاث فئات واسعة: مرنة وغير مرنة وموحدة. الطلب المرن أو العرض المرن هو الطلب الذي تكون فيه المرونة أكبر من واحد، مما يشير إلى استجابة عالية للتغيرات في السعر. تشير المرونة التي تقل عن واحدة إلى استجابة منخفضة لتغيرات الأسعار وتتوافق مع الطلب غير المرن أو العرض غير المرن. تشير المرونة الموحدة إلى الاستجابة النسبية للطلب أو العرض، على النحو الملخص في الجدول 1.
| إذا. | ثم. | ويسمى... |
| \(\%\,change\,in\,quantity\,\gt\,\%\,change\,in\,price\) | \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,\gt\,1\) | مرن |
| \(\%\,change\,in\,quantity\,=\,\%\,change\,in\,price\) | \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,=\,1\) | وحدوي |
| \(\%\,change\,in\,quantity\,\lt\,\%\,change\,in\,price\) | \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,\lt\,1\) | غير مرن |
الجدول 1: مرن وغير مرن وموحد: ثلاث حالات من المرونة
ملاحظة
قبل أن ندخل في التفاصيل الدقيقة للمرونة، استمتع بهذه المقالة عن المرونة وأسعار التذاكر في Super Bowl.
لحساب المرونة، بدلاً من استخدام تغييرات النسبة المئوية البسيطة في الكمية والسعر، يستخدم الاقتصاديون متوسط التغير في النسبة المئوية في كل من الكمية والسعر. وهذا ما يسمى طريقة منتصف المدة للمرونة، ويتم تمثيله في المعادلات التالية:
\[\%\,change\,in\,quantity\,=\,\dfrac{Q_2-Q_1}{(Q_2+Q_1)/2}\,\times\,100\]
\[\%\,change\,in\,price\,=\,\dfrac{P_2-P_1}{(P_2+P_1)/2}\,\times\,100\]
تتمثل ميزة طريقة Midpoint في أن المرء يحصل على نفس المرونة بين نقطتي سعر سواء كانت هناك زيادة أو نقصان في السعر. هذا لأن الصيغة تستخدم نفس القاعدة لكلتا الحالتين.
حساب مرونة سعر الطلب
دعونا نحسب المرونة بين النقطتين A و B وبين النقطتين G و H الموضحة في الشكل 1.

أولاً، قم بتطبيق الصيغة لحساب المرونة مع انخفاض السعر من 70 دولارًا عند النقطة B إلى 60 دولارًا عند النقطة A:
\[\%\,change\,in\,quantity\,=\,\dfrac{3000-2800}{(3000+2800)/2}\times100\]
\[=\,\dfrac{200}{2900}\times100\]
\[=\,6.9\]
\[\%\,change\,in\,price\,=\,\dfrac{60-70}{(60+70)/2}\times100\]
\[ =\,\dfrac{-10}{65}\times100\]
\[=\,-15.4\]
\[Price\,Elasticity\,of\,Demand=\,\dfrac{6.9\%}{-15.4%}\]
\[=0.45\]
لذلك، فإن مرونة الطلب بين هاتين النقطتين هي 0.45،\(\dfrac{6.9\%}{-15.4%}\) وهو مبلغ أصغر من واحد، مما يدل على أن الطلب غير مرن في هذه الفترة. دائمًا ما تكون مرونة سعر الطلب سلبية نظرًا لأن السعر والكمية المطلوبة تتحركان دائمًا في اتجاهين متعاكسين (على منحنى الطلب). وفقًا للاتفاقية، نتحدث دائمًا عن المرونة كأرقام موجبة. لذا رياضياً، نأخذ القيمة المطلقة للنتيجة. سوف نتجاهل هذه التفاصيل من الآن فصاعدًا، بينما نتذكر تفسير المرونة كأرقام موجبة.
هذا يعني أنه على طول منحنى الطلب بين النقطة B و A، إذا تغير السعر بنسبة 1٪، فإن الكمية المطلوبة ستتغير بنسبة 0.45٪. سيؤدي التغيير في السعر إلى تغيير نسبة مئوية أقل في الكمية المطلوبة. على سبيل المثال، ستؤدي زيادة السعر بنسبة 10٪ إلى انخفاض بنسبة 4.5٪ فقط في الكمية المطلوبة. سيؤدي انخفاض السعر بنسبة 10٪ إلى زيادة 4.5٪ فقط في الكمية المطلوبة. المرونة السعرية للطلب هي أرقام سلبية تشير إلى أن منحنى الطلب منحدر هبوطيًا، ولكن يتم قراءتها كقيم مطلقة. ستساعدك ميزة Work It Out التالية على حساب مرونة سعر الطلب.
ملاحظة: العثور على مرونة سعر الطلب
احسب مرونة سعر الطلب باستخدام البيانات الواردة في الشكل 1 لزيادة السعر من G إلى H. هل زادت المرونة أو انخفضت؟
الخطوة 1. نحن نعلم أن:
\[Price\,Elasticity\,of\,Demand=\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\]
الخطوة 2. من صيغة Midpoint نعلم ما يلي:
\[\%\,change\,in\,quantity\,=\,\dfrac{Q_2-Q_1}{(Q_2+Q_1)/2}\,\times\,100\]
\[\%\,change\,in\,price\,=\,\dfrac{P_2-P_1}{(P_2+P_1)/2}\,\times\,100\]
الخطوة 3. لذلك يمكننا استخدام القيم الواردة في الشكل في كل معادلة:
\[\%\,change\,in\,quantity\,=\,\dfrac{1600-1800}{(1600+1800)/2}\,\times\,100\]
\[=\,\dfrac{-200}{1700}\,\times\,100\]
\[=\,-11.76\]
\[\%\,change\,in\,price\,= \,\dfrac{130-120}{(130+120)/2}\,\times\,100\]
\[=\,\dfrac{10}{125}\,\times\,100\]
\[=\,8.0\]
الخطوة 4. بعد ذلك، يمكن استخدام هذه القيم لتحديد مرونة سعر الطلب:
\[Price\,Elasticity\,of\,Demand=\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\]
\[=\dfrac{-11.76}{8}\]
\[=1.47\]
لذلك، مرونة الطلب من G إلى H 1.47. زاد حجم المرونة (بالقيمة المطلقة) مع تقدمنا على طول منحنى الطلب من النقاط A إلى B. تذكر أن المرونة بين هاتين النقطتين كانت 0.45. كان الطلب غير مرن بين النقطتين A و B ومرنًا بين النقطتين G و H. وهذا يوضح لنا أن مرونة سعر الطلب تتغير عند نقاط مختلفة على طول منحنى الطلب المستقيم.
حساب مرونة سعر العرض
افترض أن الشقة تستأجر 650 دولارًا شهريًا وبهذا السعر يتم استئجار 10000 وحدة كما هو موضح في الشكل 2. عندما يرتفع السعر إلى 700 دولار شهريًا، يتم توفير 13000 وحدة في السوق. ما هي النسبة المئوية لزيادة المعروض من الشقق؟ ما هي حساسية السعر؟
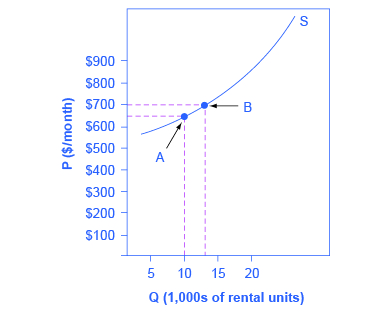
باستخدام طريقة نقطة الوسط،
\[\%\,change\,in\,quantity\,=\,\dfrac{13000-10000}{(13000+10000)/2}\,\times\,100\]
\[=\,\dfrac{3000}{11500}\,\times\,100\]
\[=\,26.1\]
\[\%\,change\,in\,price\,= \,\dfrac{\$700-\$600}{(\$700+\$600)/2}\,\times\,100\]
\[=\,\dfrac{50}{650}\,\times\,100\]
\[=\,7.69\]
\[Price\,Elasticity\,of\,Supply=\dfrac{26.1\%}{7.69\%}\]
\[=3.39\]
مرة أخرى، كما هو الحال مع مرونة الطلب، لا تتبع مرونة العرض أي وحدات. المرونة هي نسبة تغيير بنسبة مئوية واحدة إلى تغيير آخر في النسبة المئوية - لا أكثر - ويتم قراءتها كقيمة مطلقة. في هذه الحالة، يؤدي ارتفاع السعر بنسبة 1٪ إلى زيادة الكمية الموردة بنسبة 3.5٪. تعني مرونة العرض الأكبر من واحد أن النسبة المئوية للتغير في الكمية الموردة ستكون أكبر من تغيير السعر بنسبة واحد بالمائة. إذا بدأت تتساءل عما إذا كان مفهوم المنحدر مناسبًا لهذا الحساب، فاقرأ مربع Clear It Up التالي.
ملاحظة: هل المرونة هي المنحدر؟
من الخطأ الشائع الخلط بين منحدر منحنى العرض أو الطلب ومرونته. المنحدر هو معدل التغير في الوحدات على طول المنحنى، أو الارتفاع/الجري (التغيير في y فوق التغيير في x). على سبيل المثال، في الشكل 1، كل نقطة موضحة في منحنى الطلب، ينخفض السعر بمقدار 10 دولارات ويزيد عدد الوحدات المطلوبة بمقدار 200. لذا فإن المنحدر هو -10/200 على طول منحنى الطلب بالكامل ولا يتغير. ومع ذلك، تتغير مرونة السعر على طول المنحنى. كانت المرونة بين النقطتين A و B 0.45 وزادت إلى 1.47 بين النقطتين G و H. المرونة هي النسبة المئوية للتغير، وهي عملية حسابية مختلفة عن المنحدر ولها معنى مختلف.
عندما نكون في الطرف العلوي من منحنى الطلب، حيث يكون السعر مرتفعًا والكمية المطلوبة منخفضة، فإن التغيير الطفيف في الكمية المطلوبة، حتى في وحدة واحدة، على سبيل المثال، يكون كبيرًا جدًا من حيث النسبة المئوية. سيكون التغيير في سعر الدولار، على سبيل المثال، أقل أهمية بكثير من حيث النسبة المئوية مما كان سيحدث في أسفل منحنى الطلب. وبالمثل، في الجزء السفلي من منحنى الطلب، سيكون تغيير الوحدة الواحدة عندما تكون الكمية المطلوبة عالية صغيرًا كنسبة مئوية.
لذلك، عند أحد طرفي منحنى الطلب، حيث يكون لدينا تغيير كبير في النسبة المئوية في الكمية المطلوبة مقابل تغيير نسبة مئوية صغيرة في السعر، ستكون قيمة المرونة مرتفعة، أو سيكون الطلب مرنًا نسبيًا. حتى مع نفس التغيير في السعر ونفس التغيير في الكمية المطلوبة، في الطرف الآخر من منحنى الطلب تكون الكمية أعلى بكثير، والسعر أقل بكثير، وبالتالي فإن النسبة المئوية للتغير في الكمية المطلوبة تكون أصغر والنسبة المئوية للتغير في السعر أعلى بكثير. وهذا يعني أنه في الجزء السفلي من المنحنى سيكون لدينا بسط صغير فوق قاسم كبير، وبالتالي فإن مقياس المرونة سيكون أقل بكثير، أو غير مرن.
عندما نتحرك على طول منحنى الطلب، ترتفع قيم الكمية والسعر أو تنخفض، اعتمادًا على الطريقة التي نتحرك بها، وبالتالي فإن النسب المئوية، على سبيل المثال، لفرق السعر البالغ 1 دولار أو فرق وحدة واحدة في الكمية، ستتغير أيضًا، مما يعني أن نسب تلك النسب ستتغير.
المفاهيم الأساسية والملخص
تقيس مرونة السعر استجابة الكمية المطلوبة أو الموردة من السلعة للتغير في سعرها. يتم حسابها كنسبة مئوية للتغير في الكمية المطلوبة (أو الموردة) مقسومًا على النسبة المئوية للتغير في السعر. يمكن وصف المرونة بأنها مرنة (أو سريعة الاستجابة)، أو مرنة الوحدة، أو غير مرنة (غير مستجيبة للغاية). تشير منحنيات الطلب أو العرض المرنة إلى أن الكمية المطلوبة أو الموردة تستجيب لتغيرات الأسعار بطريقة أكبر من النسبية. منحنى الطلب أو العرض غير المرن هو المنحنى الذي يؤدي فيه تغير نسبة مئوية معينة في السعر إلى تغيير نسبة مئوية أقل في الكمية المطلوبة أو الموردة. تعني المرونة الموحدة أن تغير النسبة المئوية المعينة في السعر يؤدي إلى تغيير نسبة مئوية متساوية في الكمية المطلوبة أو الموردة.
مسرد المصطلحات
- الطلب المرن
- عندما تكون مرونة الطلب أكبر من واحد، مما يشير إلى استجابة عالية للكمية المطلوبة أو الموردة للتغيرات في الأسعار
- إمدادات مرنة
- عندما تكون مرونة أي من الإمدادات أكبر من واحد، مما يشير إلى استجابة عالية للكمية المطلوبة أو الموردة للتغيرات في الأسعار
- مرونة
- مفهوم اقتصادي يقيس استجابة متغير واحد للتغيرات في متغير آخر
- الطلب غير المرن
- عندما تكون مرونة الطلب أقل من واحد، مما يشير إلى أن الزيادة بنسبة 1 في المائة في السعر الذي يدفعه المستهلك تؤدي إلى تغيير أقل من 1 في المائة في المشتريات (والعكس صحيح)؛ وهذا يشير إلى استجابة منخفضة من قبل المستهلكين لتغيرات الأسعار
- إمدادات غير مرنة
- عندما تكون مرونة العرض أقل من واحد، مما يشير إلى أن الزيادة بنسبة 1 في المائة في السعر المدفوع للشركة ستؤدي إلى زيادة أقل من 1 في المائة في إنتاج الشركة؛ وهذا يشير إلى استجابة منخفضة للشركة لزيادات الأسعار (والعكس صحيح إذا انخفضت الأسعار)
- مرونة السعر
- العلاقة بين النسبة المئوية للتغير في السعر مما يؤدي إلى تغيير النسبة المئوية المقابلة في الكمية المطلوبة أو الموردة
- مرونة سعر الطلب
- النسبة المئوية للتغير في الكمية المطلوبة من السلعة أو الخدمة قسمة النسبة المئوية للتغير في السعر
- مرونة سعر العرض
- النسبة المئوية للتغير في الكمية الموردة مقسومًا على النسبة المئوية للتغير في السعر
- مرونة وحدوية
- عندما تكون المرونة المحسوبة مساوية لتلك التي تشير إلى أن التغيير في سعر السلعة أو الخدمة يؤدي إلى تغيير نسبي في الكمية المطلوبة أو الموردة


