8.3: Hyperbola

Malengo ya kujifunza

• Pata vertices ya hyperbola na foci.
• Andika equations ya hyperbolas katika fomu ya kawaida.
• Grafu hyperbolas katikati ya asili.
• Grafu hyperbolas si katikati ya asili.
• Tatua matatizo yaliyotumika yanayohusisha hyperbolas.

Je! Njia za comets, booms supersonic, nguzo za kale za Kigiriki, na minara ya baridi ya rasimu ya asili ina sawa? Wanaweza wote kutajwa na aina hiyo ya conic. Kwa mfano, wakati kitu kinachoendelea kwa kasi zaidi kuliko kasi ya sauti, wimbi la mshtuko katika fomu ya koni linaundwa. Sehemu ya conic hutengenezwa wakati wimbi linakabiliana na ardhi, na kusababisha boom ya sauti (Kielelezo\(\PageIndex{1}\)).

Kielelezo\(\PageIndex{1}\): Mshtuko wimbi intersecting ardhi aina sehemu ya conic na matokeo katika boom Sonic.

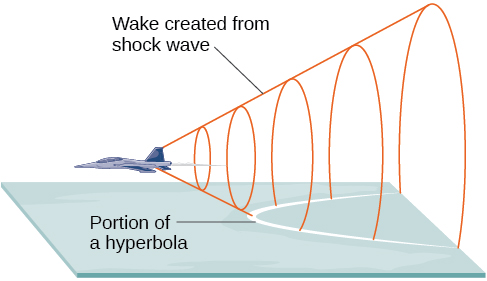
Watu wengi ni ukoo na boom Sonic iliyoundwa na ndege supersonic, lakini binadamu walikuwa kuvunja kizuizi sauti muda mrefu kabla ya ndege ya kwanza supersonic. Ufa wa mjeledi hutokea kwa sababu ncha inazidi kasi ya sauti. Risasi zilizopigwa kutoka kwa silaha nyingi pia huvunja kizuizi cha sauti, ingawa bangili ya bunduki kawaida huzidi sauti ya boom ya sauti.

Kuweka vipeo na Foci ya Hyperbola

Katika jiometri ya uchambuzi, hyperbola ni sehemu ya conic inayoundwa na kuingiliana koni ya mviringo ya mviringo na ndege kwa pembe kama vile nusu zote za koni zimeunganishwa. Mfululizo huu hutoa curves mbili zisizo na mipaka ambazo ni picha za kioo za kila mmoja (Kielelezo\(\PageIndex{2}\)).

Kielelezo\(\PageIndex{2}\): hyperbola

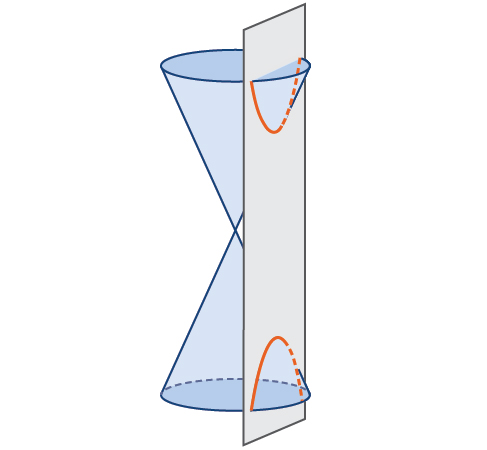
Kama duaradufu, hyperbola pia inaweza kuelezwa kama seti ya pointi katika ndege ya kuratibu. Hyperbola ni seti ya pointi zote\((x,y)\) katika ndege kama kwamba tofauti ya umbali kati\((x,y)\) na foci ni mara kwa mara chanya.

Angalia kwamba ufafanuzi wa hyperbola ni sawa na ule wa ellipse. Tofauti ni kwamba hyperbola inafafanuliwa kulingana na tofauti ya umbali mbili, wakati duaradufu hufafanuliwa kwa suala la jumla ya umbali mbili.

Kama ilivyo na ellipse, kila hyperbola ina shaba mbili za ulinganifu. Mhimili wa transverse ni sehemu ya mstari ambayo hupita katikati ya hyperbola na ina alama kama mwisho wake. The foci uongo juu ya mstari ambayo ina mhimili transverse. Mhimili wa conjugate ni perpendicular kwa mhimili transverse na ina ushirikiano vertices kama mwisho wake. Katikati ya hyperbola ni midpoint ya axes transverse na conjugate, ambapo wao intersect. Kila hyperbola pia ina asymptotes mbili zinazopita katikati yake. Kama hyperbola inapungua kutoka katikati, matawi yake yanakaribia asymptotes hizi. Mstatili wa kati wa hyperbola unazingatia asili na pande zinazopita kila vertex na vertex; ni chombo muhimu cha kuchora hyperbola na asymptotes yake. Ili kuchora asymptotes ya hyperbola, tu mchoro na kupanua diagonals ya mstatili kati (Kielelezo\(\PageIndex{3}\)).

Kielelezo\(\PageIndex{3}\): Vipengele muhimu vya hyperbola

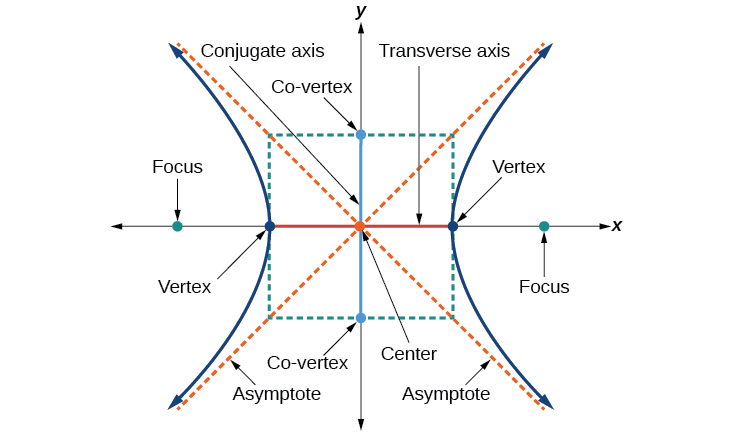
Katika sehemu hii, tutapunguza majadiliano yetu kwa hyperbolas ambazo zimewekwa kwa wima au usawa katika ndege ya kuratibu; axes itakuwa ama kulala au kuwa sawa na\(x\) - na\(y\) -axes. Tutachunguza kesi mbili: wale ambao ni katikati ya asili, na wale ambao ni katikati katika hatua nyingine zaidi ya asili.

Kupata Equation ya Ellipse unaozingatia Mwanzo

Hebu\((−c,0)\) na\((c,0)\) uwe foci ya hyperbola iliyozingatia asili. Hyperbola ni seti ya pointi zote\((x,y)\) kama kwamba tofauti ya umbali kutoka\((x,y)\) kwa foci ni mara kwa mara. Angalia Kielelezo\(\PageIndex{4}\).

Kielelezo\(\PageIndex{4}\)

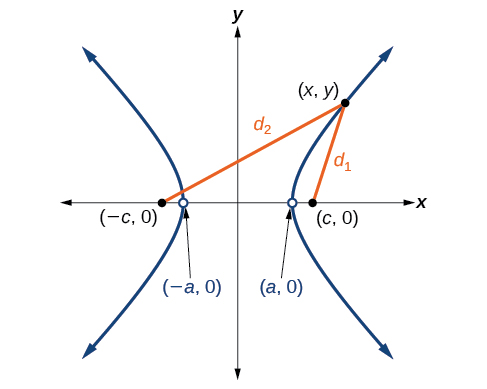
Ikiwa\((a,0)\) ni vertex ya hyperbola, umbali kutoka\((−c,0)\) kwa\((a,0)\) ni\(a−(−c)=a+c\). Umbali kutoka\((c,0)\) kwa\((a,0)\) ni\(c−a\). Jumla ya umbali kutoka foci hadi vertex ni

\((a+c)−(c−a)=2a\)

Kama\((x,y)\) ni hatua juu ya hyperbola, tunaweza kufafanua vigezo zifuatazo:

\(d_2=\)umbali kutoka\((−c,0)\) kwa\((x,y)\)

\(d_1=\)umbali kutoka\((c,0)\) kwa\((x,y)\)

Kwa ufafanuzi wa hyperbola,\(d_2−d_1\) ni mara kwa mara kwa hatua yoyote\((x,y)\) juu ya hyperbola. Tunajua kwamba tofauti ya umbali huu ni\(2a\) kwa vertex\((a,0)\). Inafuata kwamba\(d_2−d_1=2a\) kwa hatua yoyote juu ya hyperbola. Kama ilivyo na kupatikana kwa equation ya ellipse, tutaanza kwa kutumia formula ya umbali. Wengine wa derivation ni algebraic. Linganisha derivation hii na moja kutoka sehemu ya awali ya ellipses.

\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]

Equation hii inafafanua hyperbola unaozingatia asili na vipeo\((\pm a,0)\) na vyeo vya ushirikiano\((0,\pm b)\).

AINA YA KAWAIDA YA EQUATION YA HYPERBOLA NA KITUO\((0,0)\)

Aina ya kawaida ya equation ya hyperbola na katikati\((0,0)\) na mhimili transverse juu ya\(x\) -axis ni

\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)

wapi

• urefu wa mhimili wa transverse ni\(2a\)
• kuratibu za vipeo ni\((\pm a,0)\)
• urefu wa mhimili wa conjugate ni\(2b\)
• kuratibu ya vyeo vya ushirikiano ni\((0,\pm b)\)
• umbali kati ya foci ni\(2c\), wapi\(c^2=a^2+b^2\)
• kuratibu ya foci ni\((\pm c,0)\)
• equations ya asymptotes ni\(y=\pm \dfrac{b}{a}x\)

Angalia Kielelezo\(\PageIndex{5a}\).

Aina ya kawaida ya equation ya hyperbola na katikati\((0,0)\) na mhimili transverse juu ya\(y\) -axis ni

\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)

wapi

• urefu wa mhimili wa transverse ni\(2a\)
• kuratibu za vipeo ni\((0,\pm a)\)
• urefu wa mhimili wa conjugate ni\(2b\)
• kuratibu ya vyeo vya ushirikiano ni\((\pm b,0)\)
• umbali kati ya foci ni\(2c\), wapi\(c^2=a^2+b^2\)
• kuratibu ya foci ni\((0,\pm c)\)
• equations ya asymptotes ni\(y=\pm \dfrac{a}{b}x\)

Angalia Kielelezo\(\PageIndex{5b}\).

Kumbuka kwamba vertices, co-vertices, na foci ni kuhusiana na equation\(c^2=a^2+b^2\). Tunapopewa equation ya hyperbola, tunaweza kutumia uhusiano huu kutambua vipeo na foci zake.

Kielelezo\(\PageIndex{5}\): (a) Hyperbola ya usawa na kituo cha\((0,0)\) (b) hyperbola ya wima na kituo cha\((0,0)\)

Jinsi ya: Kutokana na equation ya hyperbola katika fomu ya kawaida, tafuta vipeo vyake na foci

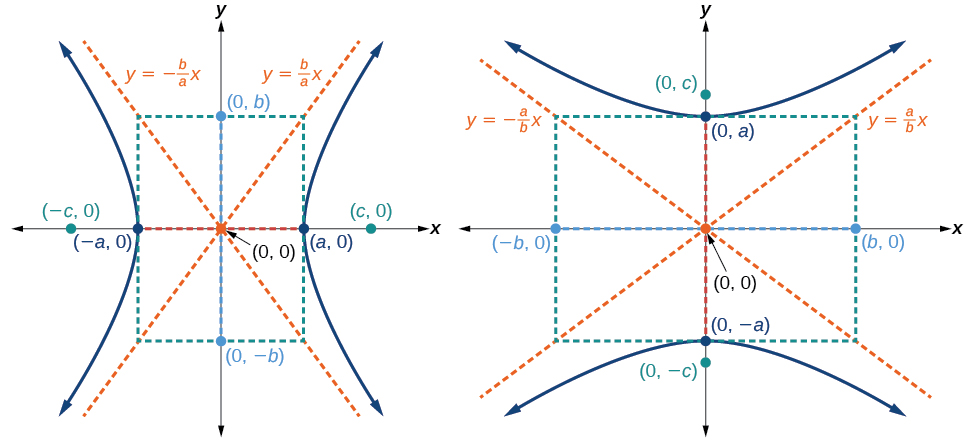
1. Kuamua kama mhimili wa transverse uongo juu ya\(x\) - au\(y\) -axis. Angalia kwamba daima\(a^2\) ni chini ya kutofautiana na mgawo mzuri. Kwa hivyo, ikiwa utaweka variable nyingine sawa na sifuri, unaweza kupata urahisi intercepts. Katika kesi ambapo hyperbola inazingatia asili, intercepts sanjari na vertices.
   • Ikiwa equation ina fomu\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), basi mhimili unaozunguka uongo juu ya\(x\) -axis. Vipande viko\((\pm a,0)\), na foci ziko\((\pm c,0)\).
   • Ikiwa equation ina fomu\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), basi mhimili unaozunguka uongo juu ya\(y\) -axis. Vipande viko\((0,\pm a)\), na foci ziko\((0,\pm c)\).
2. Tatua kwa\(a\) kutumia equation\(a=\sqrt{a^2}\).
3. Tatua kwa\(c\) kutumia equation\(c=\sqrt{a^2+b^2}\).

Mfano\(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci

Tambua vertices na foci ya hyperbola na equation\(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).

Suluhisho

Equation ina fomu\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), hivyo mhimili transverse uongo juu ya\(y\) -axis. Hyperbola inazingatia asili, hivyo vertices hutumikia kama y -intercepts ya grafu. Ili kupata vertices, kuweka\(x=0\), na kutatua kwa\(y\).

\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]

Foci iko katika\((0,\pm c)\). Kutatua kwa\(c\),

\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]

Kwa hiyo, vipeo viko\((0,\pm 7)\), na foci ziko\((0,9)\).

Zoezi\(\PageIndex{1}\)

Tambua vertices na foci ya hyperbola na equation\(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).

Jibu

Vipeo:\((\pm 3,0)\); Foci:\((\pm \sqrt{34},0)\)

Kuandika equations ya Hyperbolas katika Fomu ya Standard

Kama ilivyo kwa ellipses, kuandika equation kwa hyperbola katika fomu ya kawaida inatuwezesha kuhesabu vipengele muhimu: kituo chake, vipeo, co-vertices, foci, asymptots, na urefu na nafasi ya shoka transverse na conjugate. Kinyume chake, equation kwa hyperbola inaweza kupatikana kutokana na sifa zake muhimu. Tunaanza kwa kutafuta usawa wa kawaida wa hyperbolas unaozingatia asili. Kisha tutazingatia kutafuta usawa wa kawaida wa hyperbolas unaozingatia wakati fulani isipokuwa asili.

Hyperbolas Iliyozingatia Mwanzo

Kupitia fomu za kawaida zilizotolewa kwa hyperbolas unaozingatia\((0,0)\), tunaona kwamba vipeo, vyeo vya ushirikiano, na foci vinahusiana na equation\(c^2=a^2+b^2\). Kumbuka kuwa equation hii pia inaweza kuandikwa upya kama\(b^2=c^2−a^2\). Uhusiano huu hutumiwa kuandika equation kwa hyperbola wakati unapopewa kuratibu za foci na vipeo vyake.

Jinsi ya: Kutokana na vertices na foci ya hyperbola unaozingatia\((0,0)\), write its equation in standard form

1. Kuamua kama mhimili wa transverse uongo juu ya\(x\) - au\(y\) -axis.
   • Ikiwa kuratibu zilizopewa za vertices na foci zina fomu\((\pm a,0)\) na\((\pm c,0)\), kwa mtiririko huo, basi mhimili wa transverse ni\(x\) -axis. Tumia fomu ya kawaida\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
   • Ikiwa kuratibu zilizopewa za vertices na foci zina fomu\((0,\pm a)\) na\((0,\pm c)\), kwa mtiririko huo, basi mhimili wa transverse ni\(y\) -axis. Tumia fomu ya kawaida\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
2. Kupata\(b^2\) kutumia equation\(b^2=c^2−a^2\).
3. Badilisha maadili kwa\(a^2\) na\(b^2\) ndani ya fomu ya kiwango cha equation iliyowekwa katika Hatua ya 1.

Mfano\(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices

Je, ni usawa wa fomu ya kawaida ya hyperbola ambayo ina vertices\((\pm 6,0)\) na foci\((\pm 2\sqrt{10},0)\)?

Suluhisho

Vipande na foci ni juu ya\(x\) -axis. Hivyo, equation kwa hyperbola itakuwa na fomu\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).

Vipeo ni\((\pm 6,0)\), hivyo\(a=6\) na\(a^2=36\).

Foci ni\((\pm 2\sqrt{10},0)\), hivyo\(c=2\sqrt{10}\) na\(c^2=40\).

Kutatua kwa\(b^2\), tuna

\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]

Hatimaye, sisi badala\(a^2=36\) na\(b^2=4\) katika hali ya kiwango cha equation,\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). Equation ya hyperbola ni\(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), kama inavyoonekana katika Kielelezo\(\PageIndex{6}\).

Kielelezo\(\PageIndex{6}\)

Zoezi\(\PageIndex{2}\)

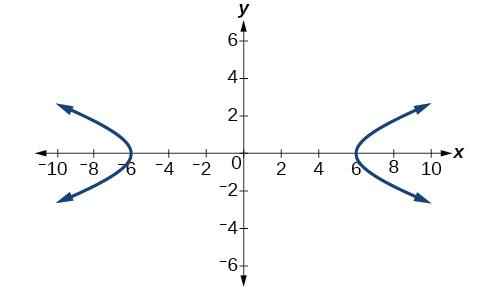
Je, ni usawa wa fomu ya kawaida ya hyperbola ambayo ina vertices\((0,\pm 2)\) na foci\((0,\pm 2\sqrt{5})\)?

Jibu

\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)

Hyperbolas Sio katikati ya Mwanzo

Kama grafu kwa equations nyingine, grafu ya hyperbola inaweza kutafsiriwa. Ikiwa hyperbola hutafsiriwa\(h\) vitengo kwa usawa na\(k\) vitengo kwa wima, katikati ya hyperbola itakuwa\((h,k)\). Matokeo ya tafsiri hii katika hali ya kawaida ya equation tuliyoona hapo awali, na\(x\) kubadilishwa\((x−h)\) na\(y\) kubadilishwa na\((y−k)\).

AINA YA KAWAIDA YA EQUATION YA HYPERBOLA NA KITUO\((H, K)\)

Fomu ya kawaida ya equation ya hyperbola na katikati\((h,k)\) na mhimili unaozunguka sambamba na\(x\) -axis ni

\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]

wapi

• urefu wa mhimili wa transverse ni\(2a\)
• kuratibu za vipeo ni\((h\pm a,k)\)
• urefu wa mhimili wa conjugate ni\(2b\)
• kuratibu ya vyeo vya ushirikiano ni\((h,k\pm b)\)
• umbali kati ya foci ni\(2c\), wapi\(c^2=a^2+b^2\)
• kuratibu ya foci ni\((h\pm c,k)\)

Asymptotes ya hyperbola sanjari na diagonals ya mstatili kati. Urefu wa mstatili ni\(2a\) na upana wake ni\(2b\). Miteremko ya diagonals ni\(\pm \dfrac{b}{a}\), na kila diagonal hupita katikati\((h,k)\). Kutumia formula ya mteremko wa uhakika, ni rahisi kuonyesha kwamba equations ya asymptotes ni\(y=\pm \dfrac{b}{a}(x−h)+k\). Angalia Kielelezo\(\PageIndex{7a}\).

Fomu ya kawaida ya equation ya hyperbola na katikati\((h,k)\) na mhimili unaozunguka sambamba na\(y\) -axis ni

\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]

wapi

• urefu wa mhimili wa transverse ni\(2a\)
• kuratibu za vipeo ni\((h,k\pm a)\)
• urefu wa mhimili wa conjugate ni\(2b\)
• kuratibu ya vyeo vya ushirikiano ni\((h\pm b,k)\)
• umbali kati ya foci ni\(2c\), wapi\(c^2=a^2+b^2\)
• kuratibu ya foci ni\((h,k\pm c)\)

Kutumia hoja hapo juu, usawa wa asymptotes ni\(y=\pm \dfrac{a}{b}(x−h)+k\). Angalia Kielelezo\(\PageIndex{7b}\).

Kielelezo\(\PageIndex{7}\): (a) Hyperbola ya usawa na kituo cha\((h,k)\) (b) hyperbola ya wima na kituo cha\((h,k)\)

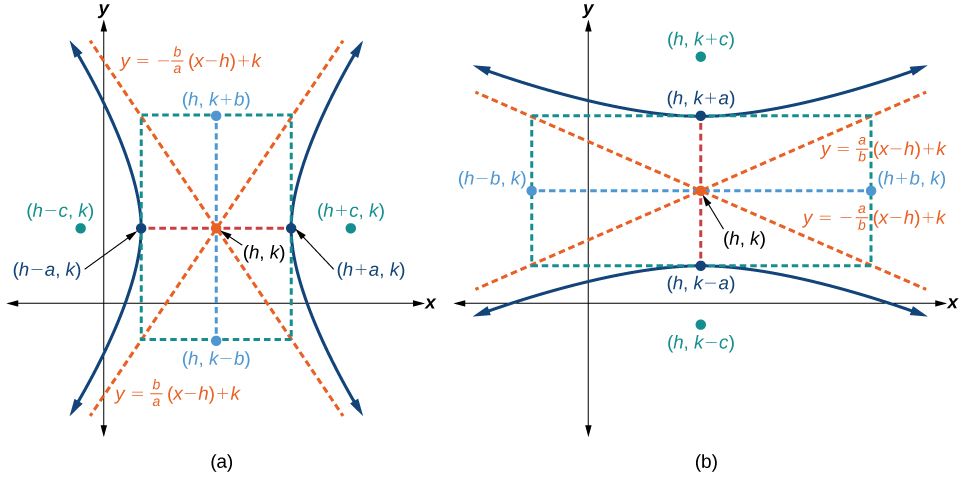
Kama hyperbolas unaozingatia asili, hyperbolas iliyozingatia kwa hatua\((h,k)\) ina vipeo, vyeo vya ushirikiano, na foci zinazohusiana na equation\(c^2=a^2+b^2\). Tunaweza kutumia uhusiano huu pamoja na kanuni za midpoint na umbali ili kupata equation ya kawaida ya hyperbola wakati vipeo na foci vinapewa.

Jinsi ya: Kutokana na vertices na foci ya hyperbola unaozingatia\((h,k)\),write its equation in standard form

1. Kuamua kama mhimili wa transverse ni sawa na\(x\) - au\(y\) -axis.
   • Ikiwa\(y\) -kuratibu ya vertices iliyotolewa na foci ni sawa, basi mhimili wa transverse ni sawa na\(x\) -axis. Tumia fomu ya kawaida\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
   • Ikiwa\(x\) -kuratibu ya vertices iliyotolewa na foci ni sawa, basi mhimili wa transverse ni sawa na\(y\) -axis. Tumia fomu ya kawaida\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
2. Tambua katikati ya hyperbola\((h,k)\), kwa kutumia formula ya midpoint na kuratibu zilizopewa kwa vipeo.
3. Pata\(a^2\) kwa kutatua kwa urefu wa mhimili unaozunguka\(2a\), ambayo ni umbali kati ya vipeo vilivyopewa.
4. Pata\(c^2\) kutumia\(h\) na\(k\) kupatikana katika Hatua ya 2 pamoja na kuratibu zilizopewa kwa foci.
5. Tatua kwa\(b^2\) kutumia equation\(b^2=c^2−a^2\).
6. Badilisha maadili kwa\(h\),\(k\)\(a^2\), na\(b^2\) katika fomu ya kawaida ya equation iliyowekwa katika Hatua ya 1.

Mfano\(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices

Je, ni fomu ya kawaida ya usawa wa hyperbola ambayo ina vertices\((0,−2)\) na\((6,−2)\) na foci katika\((−2,−2)\) na\((8,−2)\)?

Suluhisho

\(y\)Kuratibu -ya vertices na foci ni sawa, hivyo mhimili transverse ni sawa na\(x\) -axis. Hivyo, equation ya hyperbola itakuwa na fomu

\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)

Kwanza, tunatambua kituo hicho,\((h,k)\). Kituo hicho ni nusu kati ya vipeo\((0,−2)\) na\((6,−2)\). Kutumia formula ya midpoint, tuna

\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)

Kisha, tunapata\(a^2\). Urefu wa mhimili wa transverse\(2a\), umefungwa na vertices. Kwa hiyo, tunaweza kupata\(a^2\) kwa kutafuta umbali kati ya\(x\) -kuratibu ya vipeo.

\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]

Sasa tunahitaji kupata\(c^2\). Kuratibu za foci ni\((h\pm c,k)\). Hivyo\((h−c,k)=(−2,−2)\) na\((h+c,k)=(8,−2)\). Tunaweza kutumia\(x\) -kuratibu kutoka kwa mojawapo ya pointi hizi kutatua kwa\(c\). Kutumia uhakika\((8,−2)\), na kubadilisha\(h=3\),

\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]

Kisha, tatua kwa\(b^2\) kutumia equation\(b^2=c^2−a^2\):

\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]

Hatimaye, badala ya maadili kupatikana kwa\(h\)\(k\),\(a^2\), na\(b^2\) katika hali ya kiwango cha equation.

\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)

Zoezi\(\PageIndex{3}\)

Je, ni fomu ya kawaida ya usawa wa hyperbola ambayo ina vertices\((1,−2)\)\((1,8)\) na foci\((1,−10)\) na\((1,16)\)?

Jibu

\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)

Graphing Hyperbolas Centered katika Mwanzo

Tunapokuwa na equation katika hali ya kawaida kwa hyperbola unaozingatia katika asili, tunaweza kutafsiri sehemu zake kutambua sifa muhimu za grafu yake: kituo, vipeo, co-vertices, asymptotes, foci, na urefu na nafasi ya shoka transverse na conjugate. Kwa grafu hyperbolas iliyozingatia asili, tunatumia fomu\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) ya kawaida ya hyperbolas ya usawa na fomu\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) ya kawaida ya hyperbolas wima.

jinsi ya: Kutokana kiwango fomu equation kwa hyperbola unaozingatia katika\((0,0)\), sketch the graph

1. Kuamua ni aina gani ya fomu za kawaida zinazotumika kwa equation iliyotolewa.
2. Tumia fomu ya kawaida iliyotambuliwa katika Hatua ya 1 ili kuamua nafasi ya mhimili wa transverse; kuratibu kwa vertices, co-vertices, na foci; na equations kwa asymptotes.
   • Ikiwa equation iko katika fomu\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), basi
     • mhimili wa transverse ni juu ya\(x\) -axis
     • kuratibu za vipeo ni\ (\ pm a,0)\ 0
     • kuratibu ya vyeo vya ushirikiano ni\((0,\pm b)\)
     • kuratibu ya foci ni\((\pm c,0)\)
     • equations ya asymptotes ni\(y=\pm \dfrac{b}{a}x\)
   • Ikiwa equation iko katika fomu\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), basi
     • mhimili wa transverse ni juu ya\(y\) -axis
     • kuratibu za vipeo ni\((0,\pm a)\)
     • kuratibu ya vyeo vya ushirikiano ni\((\pm b,0)\)
     • kuratibu ya foci ni\((0,\pm c)\)
     • equations ya asymptotes ni\(y=\pm \dfrac{a}{b}x\)
3. Tatua kwa kuratibu za foci kwa kutumia equation\(c=\pm \sqrt{a^2+b^2}\).
4. Panda vertices, co-vertices, foci, na asymptotes katika ndege ya kuratibu, na kuteka curve laini ili kuunda hyperbola.

Mfano\(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form

Grafu hyperbola iliyotolewa na equation\(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Tambua na uandike alama, vyeo vya ushirikiano, foci, na asymptotes.

Suluhisho

Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Hivyo, mhimili transverse ni juu ya\(y\) -axis

Kuratibu za vipeo ni\((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)

Kuratibu za vyeo vya ushirikiano ni\((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)

Kuratibu za foci ni\((0,\pm c)\) wapi\(c=\pm \sqrt{a^2+b^2}\). Kutatua kwa\(c\), tuna

\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)

Kwa hiyo, kuratibu ya foci ni\((0,\pm 10)\)

Equations ya asymptotes ni\(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)

Panda na uandike alama na vyeo vya ushirikiano, na kisha mchoro mstatili wa kati. Pande za mstatili ni sawa na axes na hupita kupitia vertices na vyeo vya ushirikiano. Mchoro na kupanua diagonals ya mstatili wa kati ili kuonyesha asymptotes. Mstatili wa kati na asymptotes hutoa mfumo unaohitajika kuchora grafu sahihi ya hyperbola. Weka alama ya foci na asymptotes, na kuteka safu ya laini ili kuunda hyperbola, kama inavyoonekana kwenye Mchoro\(\PageIndex{8}\).

Kielelezo\(\PageIndex{8}\)

Zoezi\(\PageIndex{4}\)

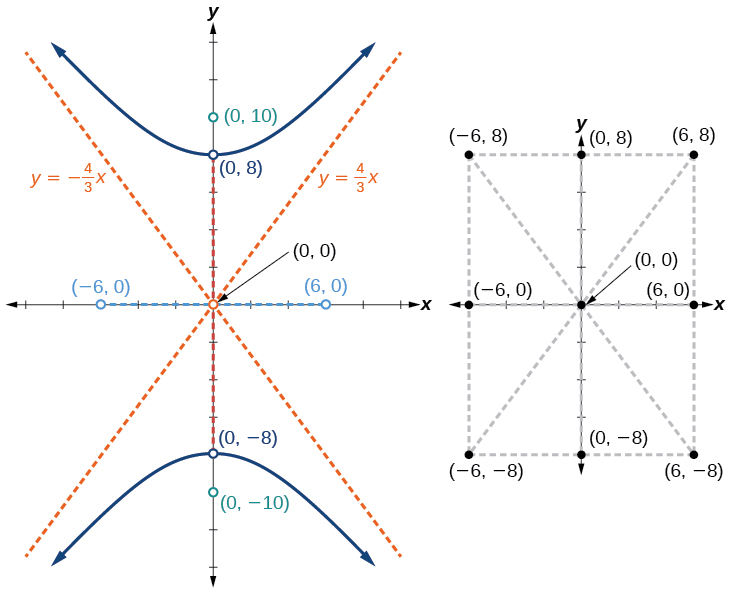
Grafu hyperbola iliyotolewa na equation\(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Tambua na uandike alama, vyeo vya ushirikiano, foci, na asymptotes.

Jibu

vertices:\((\pm 12,0)\); ushirikiano vertices:\((0,\pm 9)\); foci:\((\pm 15,0)\); asymptotes:\(y=\pm \dfrac{3}{4}x\);

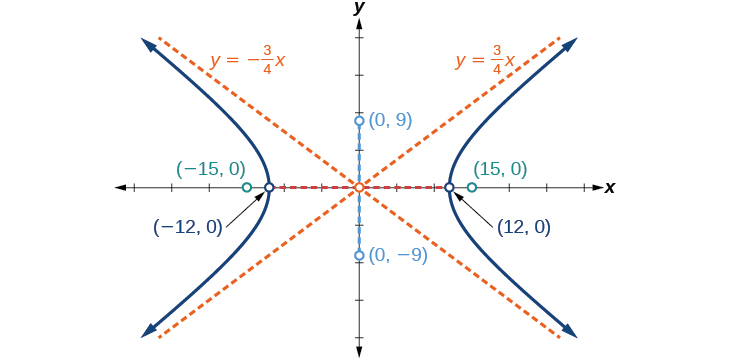
Kielelezo\(\PageIndex{9}\)

Graphing Hyperbolas Si Centered katika Mwanzo

Graphing hyperbolas katikati katika hatua\((h,k)\) nyingine zaidi ya asili ni sawa na graphing ellipses unaozingatia katika hatua nyingine zaidi ya asili. Tunatumia fomu za kawaida\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) kwa hyperbolas ya usawa, na\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) kwa hyperbolas wima. Kutoka kwa equations hizi za fomu za kawaida tunaweza kuhesabu kwa urahisi na kupanga vipengele muhimu vya grafu: kuratibu za kituo chake, vertices, co-vertices, na foci; equations ya asymptotes yake; na nafasi za axes transverse na conjugate.

Jinsi ya: Kutokana na fomu ya jumla ya hyperbola unaozingatia\((h, k)\), sketch the graph

1. Badilisha fomu ya jumla kwa fomu hiyo ya kawaida. Kuamua ni aina gani ya fomu za kawaida zinazotumika kwa equation iliyotolewa.
2. Tumia fomu ya kawaida iliyotambuliwa katika Hatua ya 1 ili kuamua nafasi ya mhimili wa transverse; kuratibu kwa kituo, vertices, co-vertices, foci; na equations kwa asymptotes.
   1. Ikiwa equation iko katika fomu\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), basi
      • mhimili wa transverse ni sawa na\(x\) -axis
      • kituo hicho ni\((h,k)\)
      • kuratibu za vipeo ni\((h\pm a,k)\)
      • kuratibu ya vyeo vya ushirikiano ni\((h,k\pm b)\)
      • kuratibu ya foci ni\((h\pm c,k)\)
      • equations ya asymptotes ni\(y=\pm \dfrac{b}{a}(x−h)+k\)
   2. Ikiwa equation iko katika fomu\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), basi
      • mhimili wa transverse ni sawa na\(y\) -axis
      • kituo hicho ni\((h,k)\)
      • kuratibu za vipeo ni\((h,k\pm a)\)
      • kuratibu ya vyeo vya ushirikiano ni\((h\pm b,k)\)
      • kuratibu ya foci ni\((h,k\pm c)\)
      • equations ya asymptotes ni\(y=\pm \dfrac{a}{b}(x−h)+k\)
3. Tatua kwa kuratibu za foci kwa kutumia equation\(c=\pm \sqrt{a^2+b^2}\).
4. Panda katikati, vertices, co-vertices, foci, na asymptotes katika ndege ya kuratibu na kuteka curve laini ili kuunda hyperbola.

Mfano\(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form

Grafu hyperbola iliyotolewa na equation\(9x^2−4y^2−36x−40y−388=0\). Tambua na uandike kituo, vipeo, vyeo vya ushirikiano, foci, na asymptotes.

Suluhisho

Anza kwa kuelezea equation katika fomu ya kawaida. Masharti ya kikundi ambayo yana variable sawa, na hoja ya mara kwa mara kwa upande wa pili wa equation.

\((9x^2−36x)−(4y^2+40y)=388\)

Fanya mgawo wa kuongoza wa kila kujieleza.

\(9(x^2−4x)−4(y^2+10y)=388\)

Jaza mraba mara mbili. Kumbuka kusawazisha equation kwa kuongeza constants sawa kwa kila upande.

\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)

Andika upya kama mraba kamilifu.

\(9{(x−2)}^2−4{(y+5)}^2=324\)

Gawanya pande zote mbili kwa muda wa mara kwa mara ili kuweka equation katika fomu ya kawaida.

\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)

Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), wapi\(a^2=36\) na\(b^2=81\), au\(a=6\) na\(b=9\). Hivyo, mhimili wa transverse ni sawa na\(x\) -axis. Inafuata kwamba:

katikati ya ellipse ni\((h,k)=(2,−5)\)

kuratibu ya vipeo ni\((h\pm a,k)=(2\pm 6,−5)\), au\((−4,−5)\) na\((8,−5)\)

kuratibu ya vyeo vya ushirikiano ni\((h,k\pm b)=(2,−5\pm 9)\), au\((2,−14)\)\((2,4)\)

kuratibu ya foci ni\((h\pm c,k)\), wapi\(c=\pm \sqrt{a^2+b^2}\). Kutatua kwa\(c\), tuna

\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)

Kwa hiyo, kuratibu za foci ni\((2−3\sqrt{13},−5)\) na\((2+3\sqrt{13},−5)\).

Ulinganisho wa asymptotes ni\(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).

Ifuatayo, tunapanga na kuandika kituo hicho, vipeo, vyeo, foci, na asymptotes na kuteka curves laini ili kuunda hyperbola, kama inavyoonekana kwenye Mchoro\(\PageIndex{10}\).

Kielelezo\(\PageIndex{10}\)

Zoezi\(\PageIndex{5}\)

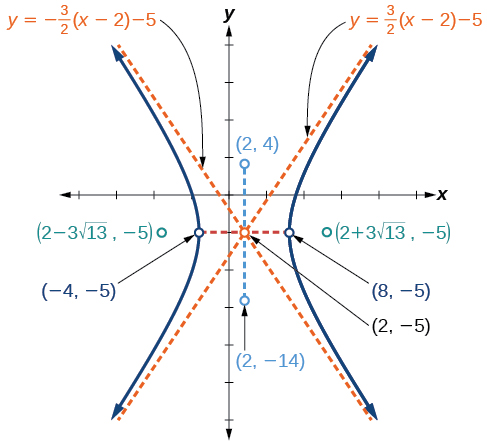
Grafu hyperbola iliyotolewa na fomu ya kawaida ya equation\(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Tambua na uandike kituo, vipeo, vyeo vya ushirikiano, foci, na asymptotes.

Jibu

kituo:\((3,−4)\); vertices:\((3,−14)\) na\((3,6)\); ushirikiano vertices:\((−5,−4)\); na\((11,−4)\); foci:\((3,−4−2\sqrt{41})\) na\((3,−4+2\sqrt{41})\); asymptotes:\(y=\pm \dfrac{5}{4}(x−3)−4\)

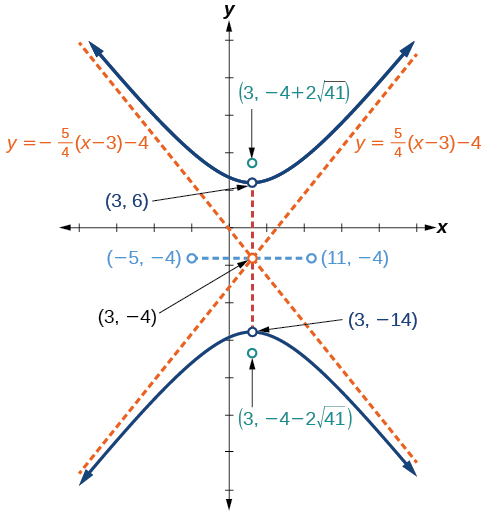
Kielelezo\(\PageIndex{11}\)

Kutatua Matatizo yaliyotumika Kuhusisha Hyperbolas

Kama tulivyojadiliwa mwanzoni mwa sehemu hii, hyperbolas zina maombi halisi ya ulimwengu katika nyanja nyingi, kama vile astronomia, fizikia, uhandisi, na usanifu. Ufanisi wa kubuni wa minara ya baridi ya hyperbolic ni ya kuvutia sana. Minara ya baridi hutumiwa kuhamisha joto la taka kwenye anga na mara nyingi hutajwa kwa uwezo wao wa kuzalisha nguvu kwa ufanisi. Kwa sababu ya fomu yao ya hyperbolic, miundo hii inaweza kuhimili upepo uliokithiri wakati inahitaji nyenzo ndogo kuliko aina nyingine yoyote ya ukubwa na nguvu zao (Kielelezo\(\PageIndex{12}\)). Kwa mfano, mnara wa\(500\) mguu unaweza kufanywa kwa shell ya saruji iliyoimarishwa tu\(6\) au\(8\) inchi pana!

Kielelezo\(\PageIndex{12}\): Minara ya baridi kwenye kituo cha nguvu cha Drax huko Kaskazini Yorkshire, Uingereza (mikopo: Les Haines, Flickr)

Minara ya kwanza ya hyperbolic iliundwa mwaka wa 1914 na ilikuwa\(35\) mita za juu. Leo, minara ndefu zaidi ya baridi iko nchini Ufaransa, imesimama\(170\) mita za ajabu. Katika Mfano\(\PageIndex{6}\) tutatumia mpangilio wa kubuni wa mnara wa baridi ili kupata equation ya hyperbolic ambayo inafanana na pande zake.

Mfano\(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas

Mpangilio wa kubuni wa mnara wa baridi unaonyeshwa kwenye Mchoro\(\PageIndex{13}\). Mnara unasimama\(179.6\) mita mrefu. Kipenyo cha juu ni\(72\) mita. Kwa karibu zaidi, pande za mnara ni\(60\) mita mbali.

Kielelezo\(\PageIndex{13}\): Mradi wa kubuni kwa mnara wa baridi wa rasimu ya asili

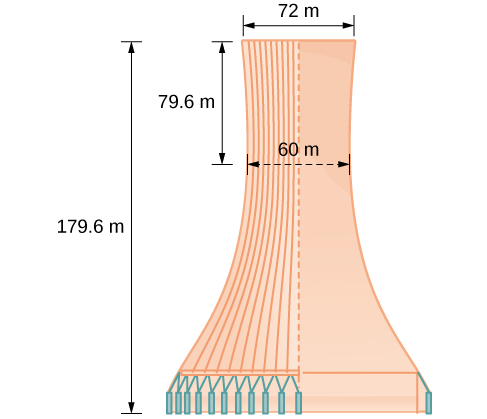
Kupata equation ya hyperbola kwamba mifano ya pande ya mnara baridi. Kudhani kwamba katikati ya hyperbola-unahitajika kwa makutano ya mistari iliyopigwa perpendicular katika takwimu-ni asili ya ndege ya kuratibu. Maadili ya mwisho ya pande zote kwa maeneo manne ya decimal.

Suluhisho

Sisi ni kuchukua katikati ya mnara ni katika asili, hivyo tunaweza kutumia fomu ya kawaida ya hyperbola usawa unaozingatia katika asili:\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), ambapo matawi ya hyperbola fomu pande za mnara baridi. Lazima tupate maadili ya\(a^2\)\(b^2\) na kukamilisha mfano.

Kwanza, tunapata\(a^2\). Kumbuka kwamba urefu wa mhimili transverse ya hyperbola ni\(2a\). Urefu huu unawakilishwa na umbali ambapo pande ziko karibu, ambazo hutolewa kama\(65.3\) mita. Hivyo,\(2a=60\). Kwa hiyo,\(a=30\) na\(a^2=900\).

Ili kutatua\(b^2\), tunahitaji kubadilisha\(x\) na\(y\) katika equation yetu kwa kutumia hatua inayojulikana. Ili kufanya hivyo, tunaweza kutumia vipimo vya mnara ili kupata hatua fulani\((x,y)\) ambayo iko kwenye hyperbola. Tutatumia kona ya juu ya kulia ya mnara ili kuwakilisha hatua hiyo. Kwa kuwa\(y\) -axis inakataza mnara,\(x\) thamani yetu inaweza kuwakilishwa na radius ya juu, au\(36\) mita. Thamani y inawakilishwa na umbali kutoka asili hadi juu, ambayo hutolewa kama\(79.6\) mita. Kwa hiyo,

\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]

Pande za mnara zinaweza kuonyeshwa na equation ya hyperbolic

\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\), au\(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)

Zoezi\(\PageIndex{6}\)

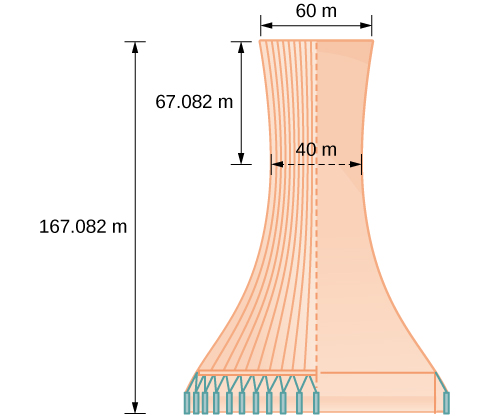
Mpangilio wa mradi wa mnara wa baridi unaonyeshwa kwenye Kielelezo\(\PageIndex{14}\). Kupata equation ya hyperbola kwamba mifano ya pande ya mnara baridi. Kudhani kwamba katikati ya hyperbola-unahitajika kwa makutano ya mistari iliyopigwa perpendicular katika takwimu-ni asili ya ndege ya kuratibu. Maadili ya mwisho ya pande zote kwa maeneo manne ya decimal.

Kielelezo\(\PageIndex{14}\)

Jibu

Pande za mnara zinaweza kuonyeshwa na equation ya hyperbolic. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\)au\(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na hyperbolas.

• Sehemu za Conic: Hyperbola Sehemu ya 1 ya 2
• Sehemu za Conic: Hyperbola Sehemu ya 2 ya 2
• Grafu Hyperbola na Kituo cha Mwanzo
• Grafu Hyperbola na Kituo si katika Mwanzo

Mlinganyo muhimu

Hyperbola, katikati ya asili, mhimili wa mzunguko kwenye x -axis	\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
Hyperbola, katikati ya asili, mhimili wa mzunguko juu ya y -axis	\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
Hyperbola, katikati\((h,k)\), mhimili unaozunguka sambamba na x -axis	\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
Hyperbola, katikati\((h,k)\), mhimili unaozunguka sambamba na y -axis	\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\)

Dhana muhimu

• Hyperbola ni seti ya pointi zote\((x,y)\) katika ndege kama kwamba tofauti ya umbali kati\((x,y)\) na foci ni mara kwa mara chanya.
• Fomu ya kawaida ya hyperbola inaweza kutumika kupata alama zake na foci. Angalia Mfano\(\PageIndex{1}\).
• Tunapopewa kuratibu za foci na vipeo vya hyperbola, tunaweza kuandika equation ya hyperbola kwa fomu ya kawaida. Angalia Mfano\(\PageIndex{2}\) na Mfano\(\PageIndex{3}\).
• Wakati kupewa equation kwa hyperbola, tunaweza kutambua vipeo yake, co-vertices, foci, asymptots, na urefu na nafasi ya shoka transverse na conjugate ili grafu hyperbola. Angalia Mfano\(\PageIndex{4}\) na Mfano\(\PageIndex{5}\).
• Hali halisi ya ulimwengu inaweza kutajwa kwa kutumia equations ya kawaida ya hyperbolas. Kwa mfano, kutokana na vipimo vya mnara wa baridi wa rasimu ya asili, tunaweza kupata equation ya hyperbolic ambayo inafanana na pande zake. Angalia Mfano\(\PageIndex{6}\).