6.5: Grafu za Kazi za Logarithmic
- Page ID
- 180894
- Tambua uwanja wa kazi ya logarithmic.
- Grafu logarithmic kazi.
Katika Sehemu ya Grafu ya Kazi za Kielelezo, tuliona jinsi kuunda uwakilishi wa kielelezo wa mfano wa kielelezo unatupa safu nyingine ya ufahamu kwa kutabiri matukio ya baadaye. Je, grafu za logarithmic zinatupa ufahamu katika hali? Kwa sababu kila kazi logarithmic ni kazi inverse ya kazi kielelezo, tunaweza kufikiria kila pato juu ya graph logarithmic kama pembejeo kwa sambamba inverse kielelezo equation. Kwa maneno mengine, logarithms hutoa sababu ya athari.
Kwa mfano, tuseme sisi kuwekeza\($2500\) katika akaunti ambayo inatoa kila mwaka riba ya 5%, imezungukwa kuendelea. Tayari tunajua kwamba usawa katika akaunti yetu kwa mwaka wowote\(t\) unaweza kupatikana kwa equation\(A=2500e^{0.05t}\).
Lakini vipi kama tulitaka kujua mwaka kwa usawa wowote? Tunataka kujenga sambamba kazi mpya kwa kubadilishana pembejeo na pato; hivyo tunahitaji kujenga mfano wa logarithmic kwa hali hii. Kwa kuchora mfano, tunaweza kuona pato (mwaka) kwa pembejeo yoyote (usawa wa akaunti). Kwa mfano, vipi kama tulitaka kujua miaka ngapi itachukua kwa uwekezaji wetu wa awali kuwa mara mbili? Kielelezo\(\PageIndex{1}\) kinaonyesha hatua hii kwenye grafu ya logarithmic.
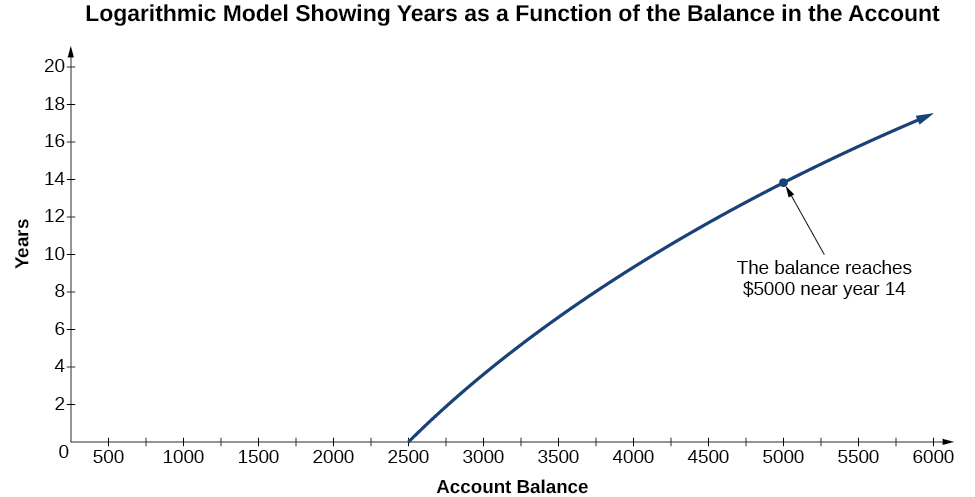
Katika sehemu hii tutajadili maadili ambayo kazi ya logarithmic inafafanuliwa, na kisha tutazingatia kuzingatia familia ya kazi za logarithmic.
Kutafuta Domain ya Kazi ya Logarithmic
Kabla ya kufanya kazi na grafu, tutaangalia uwanja (seti ya maadili ya pembejeo) ambayo kazi ya logarithmic inaelezwa.
Kumbuka kwamba kazi kielelezo hufafanuliwa kama\(y=b^x\) kwa idadi yoyote halisi\(x\) na ya mara kwa mara\(b>0\),\(b≠1\), ambapo
- uwanja wa\(y\) ni\((−\infty,\infty)\).
- mbalimbali ya\(y\) ni\((0,\infty)\).
Katika sehemu ya mwisho tulijifunza kwamba kazi ya logarithmic\(y={\log}_b(x)\) ni inverse ya kazi ya kielelezo\(y=b^x\). Hivyo, kama kazi inverse:
- uwanja wa\(y={\log}_b(x)\) ni mbalimbali ya\(y=b^x\):\((0,\infty)\).
- Mbalimbali ya\(y={\log}_b(x)\) ni uwanja wa\(y=b^x\):\((−\infty,\infty)\).
Mabadiliko ya kazi ya mzazi\(y={\log}_b(x)\) hufanya sawa na yale ya kazi nyingine. Kama vile kazi nyingine mzazi, tunaweza kutumia aina nne za mabadiliko - mabadiliko, stretches, compressions, na tafakari - kwa kazi mzazi bila kupoteza sura.
Katika Grafu ya Kazi Kielelezo tuliona kwamba mabadiliko fulani yanaweza kubadilisha mbalimbali ya\(y=b^x\). Vile vile, kutumia mabadiliko kwa kazi ya mzazi\(y={\log}_b(x)\) kunaweza kubadilisha kikoa. Wakati wa kutafuta uwanja wa kazi ya logarithmic, kwa hiyo, ni muhimu kukumbuka kuwa uwanja una idadi halisi tu. Hiyo ni, hoja ya kazi ya logarithmic lazima iwe kubwa kuliko sifuri.
Kwa mfano, fikiria\(f(x)={\log}_4(2x−3)\). Kazi hii hufafanuliwa kwa maadili yoyote ya\(x\) vile kwamba hoja, katika kesi hii\(2x−3\), ni kubwa kuliko sifuri. Ili kupata uwanja, tunaanzisha usawa na kutatua kwa\(x\):
\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&> 1.5 \qquad \text{Divide by 2} \\ \end{align*}\]
Katika notation ya muda, uwanja wa\(f(x)={\log}_4(2x−3)\) ni\((1.5,\infty)\).
- Weka usawa kuonyesha hoja kubwa kuliko sifuri.
- Kutatua kwa\(x\).
- Andika kikoa katika maelezo ya muda.
Je, ni uwanja wa\(f(x)={\log}_2(x+3)\)?
Suluhisho
Kazi ya logarithmic inaelezwa tu wakati pembejeo ni chanya, hivyo kazi hii inafafanuliwa wakati\(x+3>0\). Kutatua kukosekana kwa usawa huu,
\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]
uwanja wa\(f(x)={\log}_2(x+3)\) ni\((−3,\infty)\).
Je, ni uwanja wa\(f(x)={\log}_5(x−2)+1\)?
- Jibu
-
\((2,\infty)\)
Je, ni uwanja wa\(f(x)=\log(5−2x)\)?
Suluhisho
Kazi ya logarithmic inaelezwa tu wakati pembejeo ni chanya, hivyo kazi hii inafafanuliwa wakati\(5–2x>0\). Kutatua kukosekana kwa usawa huu,
\[\begin{align*} 5-2x&> 0 \qquad \text{The input must be positive}\\ -2x&> -5 \qquad \text{Subtract 5}\\ x&< \dfrac{5}{2} \qquad \text{Divide by -2 and switch the inequality} \end{align*}\]
uwanja wa\(f(x)=\log(5−2x)\) ni\(\left(–\infty,\dfrac{5}{2}\right)\).
Je, ni uwanja wa\(f(x)=\log(x−5)+2\)?
- Jibu
-
\((5,\infty)\)
Graphing Logarithmic Kazi
Sasa kwa kuwa tuna hisia kwa seti ya maadili ambayo kazi ya logarithmic inafafanuliwa, tunaendelea kwenye kazi za logarithmic. Familia ya kazi za logarithmic inajumuisha kazi ya mzazi\(y={\log}_b(x)\) pamoja na mabadiliko yake yote: mabadiliko, kunyoosha, compressions, na kutafakari.
Tunaanza na kazi ya mzazi\(y={\log}_b(x)\). Kwa sababu kila kazi ya logarithmic ya fomu hii ni inverse ya kazi ya kielelezo na fomu\(y=b^x\), grafu zao zitakuwa tafakari za kila mmoja kwenye mstari\(y=x\). Ili kuonyesha hili, tunaweza kuchunguza uhusiano kati ya maadili ya pembejeo na pato la\(y=2^x\) na sawa\(x={\log}_2(y)\) katika Jedwali\(\PageIndex{1}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(2^x=y\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \({\log}_2(y)=x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
Kutumia pembejeo na matokeo kutoka Jedwali\(\PageIndex{1}\), tunaweza kujenga meza nyingine kuchunguza uhusiano kati ya pointi kwenye grafu za kazi za inverse\(f(x)=2^x\) na\(g(x)={\log}_2(x)\). Angalia Jedwali\(\PageIndex{2}\).
| \(f(x)=2^x\) | \(\left(−3,\dfrac{1}{8}\right)\) | \(\left(−2,\dfrac{1}{4}\right)\) | \(\left(−1,\dfrac{1}{2}\right)\) | \((0,1)\) | \((1,2)\) | \((2,4)\) | \((3,8)\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\log}_2(x)\) | \(\left(\dfrac{1}{8},−3\right)\) | \(\left(\dfrac{1}{4},−2\right)\) | \(\left(\dfrac{1}{2},−1\right)\) | \((1,0)\) | \((2,1)\) | \((4,2)\) | \((8,3)\) |
Kama tunatarajia,\(x\) - na\(y\) -kuratibu ni kuachwa kwa ajili ya kazi inverse. Kielelezo\(\PageIndex{2}\) kinaonyesha grafu ya\(f\) na\(g\).
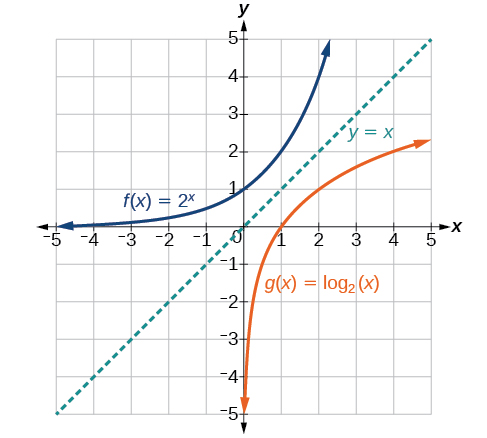
Angalia zifuatazo kutoka kwenye grafu:
- \(f(x)=2^x\)ina\(y\) -intercept katika\((0,1)\) na\(g(x)={\log}_2(x)\) ina\(x\) - intercept katika\((1,0)\).
- uwanja wa\(f(x)=2^x\),\((−\infty,\infty)\), ni sawa na aina mbalimbali ya\(g(x)={\log}_2(x)\).
- mbalimbali ya\(f(x)=2^x\),\((0,\infty)\), ni sawa na uwanja wa\(g(x)={\log}_2(x)\).
Kwa idadi yoyote halisi\(x\) na mara kwa mara\(b>0\)\(b≠1\),, tunaweza kuona sifa zifuatazo katika grafu ya\(f(x)={\log}_b(x)\):
- kazi moja kwa moja
- asymptote ya wima:\(x=0\)
- kikoa:\((0,\infty)\)
- mbalimbali:\((−\infty,\infty)\)
- \(x\)- kukatiza:\((1,0)\) na hatua muhimu\((b,1)\)
- \(y\)-kukatiza: hakuna
- kuongezeka kama\(b>1\)
- kupungua kama\(0<b<1\)
Angalia Kielelezo\(\PageIndex{3}\).
Kielelezo\(\PageIndex{4}\) inaonyesha jinsi kubadilisha msingi\(b\) katika\(f(x)={\log}_b(x)\) inaweza kuathiri grafu. Angalia kwamba grafu zinakabiliwa kwa wima kama thamani ya ongezeko la msingi. (Kumbuka: kumbuka kwamba kazi\(\ln(x)\) ina msingi\(e≈2.718\).)
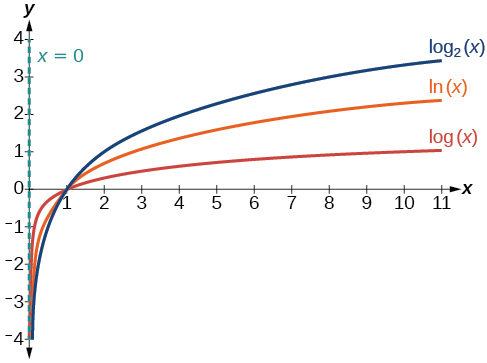
- Chora na uandike alama ya wima,\(x=0\).
- Panda x- intercept,\((1,0)\).
- Panda hatua muhimu\((b,1)\).
- Chora curve laini kupitia pointi.
- Weka kikoa\((0,\infty)\), upeo\((−\infty,\infty)\), na asymptote ya wima,\(x=0\).
Grafu\(f(x)={\log}_5(x)\). Weka kikoa, upeo, na asymptote.
Suluhisho
Kabla ya kuchora, tambua tabia na pointi muhimu za grafu.
- Kwa kuwa\(b=5\) ni kubwa kuliko moja, tunajua kazi inaongezeka. Mkia wa kushoto wa grafu utafikia asymptote ya wima\(x=0\), na mkia wa kulia utaongezeka polepole bila kufungwa.
- \(x\)Kizuizi ni\((1,0)\).
- Hatua muhimu\((5,1)\) ni kwenye grafu.
- Tunapata na kuandika alama ya asymptote, njama na kuandika alama, na kuteka safu ya laini kupitia pointi (angalia Mchoro\(\PageIndex{5}\)).
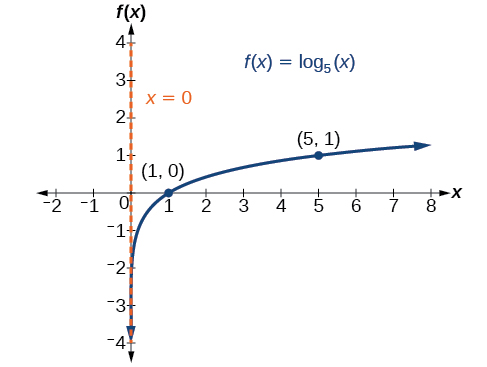
Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Grafu\(f(x)={\log}_{\tfrac{1}{5}}(x)\). Weka kikoa, upeo, na asymptote.
- Jibu
-
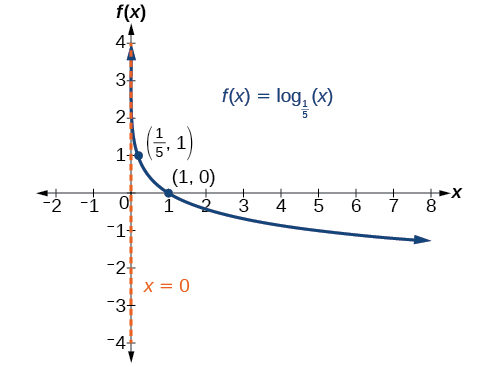
Kielelezo\(\PageIndex{6}\) Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Graphing Mabadiliko ya Kazi za Logarithmic
Kama tulivyosema mwanzoni mwa sehemu hiyo, mabadiliko ya grafu za logarithmic hufanya sawa na yale ya kazi nyingine za wazazi. Tunaweza kuhama, kunyoosha, compress, na kutafakari kazi mzazi\(y={\log}_b(x)\) bila kupoteza sura.
Graphing Shift Horizontal ya\(f(x) = log_b(x)\)
Wakati mara kwa mara\(c\) inaongezwa kwa pembejeo ya kazi ya mzazi\(f(x)={\log}_b(x)\), matokeo ni\(c\) vitengo vya kuhama kwa usawa kinyume cha ishara\(c\). Ili kutazama mabadiliko ya usawa, tunaweza kuchunguza grafu ya jumla ya kazi ya mzazi\(f(x)={\log}_b(x)\) na kwa\(c>0\) pamoja na mabadiliko ya kushoto,\(g(x)={\log}_b(x+c)\), na kuhama haki,\(h(x)={\log}_b(x−c)\). Angalia Kielelezo\(\PageIndex{7}\).
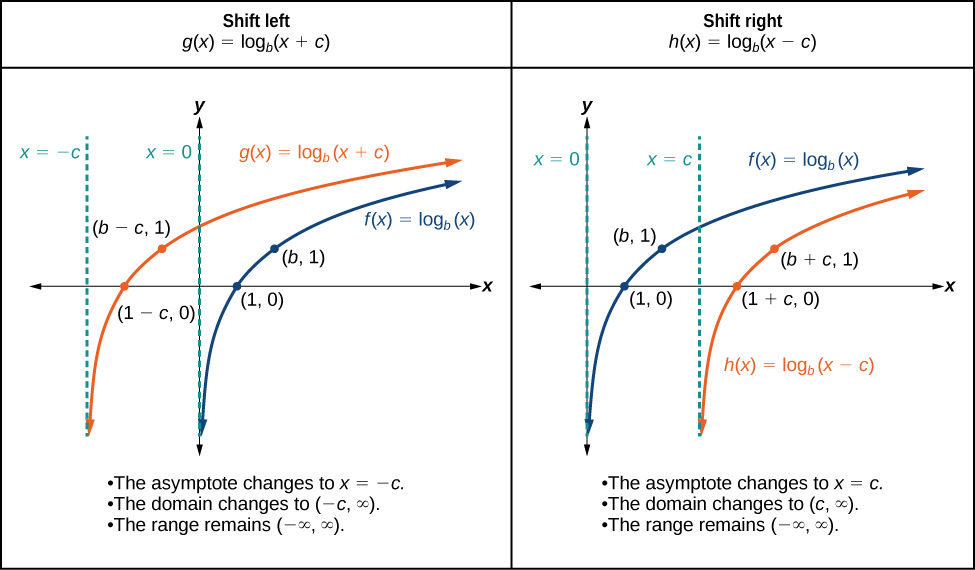
Kwa mara kwa mara yoyote\(c\), kazi\(f(x)={\log}_b(x+c)\)
- mabadiliko kazi mzazi\(y={\log}_b(x)\) kushoto\(c\) vitengo kama\(c>0\).
- mabadiliko mzazi kazi\(c\) vitengo\(y={\log}_b(x)\) haki kama\(c<0\).
- ina asymptote ya wima\(x=−c\).
- ina uwanja\((−c,\infty)\).
- ina mbalimbali\((−\infty,\infty)\).
- Tambua mabadiliko ya usawa:
- Ikiwa\(c>0\), ongeza grafu ya\(c\) vitengo vya\(f(x)={\log}_b(x)\) kushoto.
- Ikiwa\(c<0\), mabadiliko ya grafu ya\(c\) vitengo vya\(f(x)={\log}_b(x)\) kulia.
- Chora asymptote ya wima\(x=−c\).
- Tambua pointi tatu muhimu kutoka kwa kazi ya mzazi. Pata kuratibu mpya kwa kazi zilizobadilishwa kwa kuondoa\(c\) kutoka\(x\) kuratibu.
- Lebo pointi tatu.
- Domain ni\((−c,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=−c\).
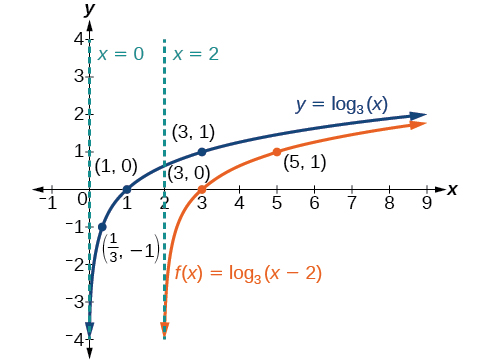
Mchoro mabadiliko ya usawa\(f(x)={\log}_3(x−2)\) pamoja na kazi yake ya mzazi. Jumuisha pointi muhimu na asymptotes kwenye grafu. Weka kikoa, upeo, na asymptote.
Suluhisho
Tangu kazi ni\(f(x)={\log}_3(x−2)\), tunaona\(x+(−2)=x–2\).
Hivyo\(c=−2\), hivyo\(c<0\). Hii ina maana sisi kuhama kazi\(f(x)={\log}_3(x)\) haki 2 vitengo.
Asymptote ya wima ni\(x=−(−2)\) au\(x=2\).
Fikiria pointi tatu muhimu kutoka kwa kazi ya mzazi\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), na\((3,1)\).
Kuratibu mpya zinapatikana kwa\(2\) kuongeza\(x\) kuratibu.
Weka alama\(\left(\dfrac{7}{3},−1\right)\),\((3,0)\), na\((5,1)\).
Kikoa ni\((2,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=2\).
Mchoro grafu ya\(f(x)={\log}_3(x+4)\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptotes kwenye grafu. Weka kikoa, upeo, na asymptote.
- Jibu
-
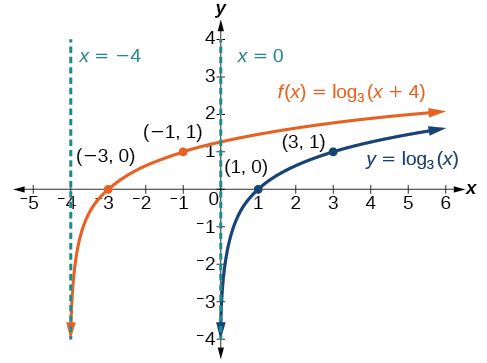
Kielelezo\(\PageIndex{9}\) Kikoa ni\((−4,\infty)\), upeo\((−\infty,\infty)\), na asymptote\(x=–4\).
Graphing Shift Wima ya\(y = log_b(x)\)
Wakati mara kwa mara\(d\) inaongezwa kwenye kazi ya mzazi\(f(x)={\log}_b(x)\), matokeo ni\(d\) vitengo vya kuhama wima katika mwelekeo wa ishara\(d\). Ili kutazama mabadiliko ya wima, tunaweza kuchunguza grafu ya jumla ya kazi ya mzazi\(f(x)={\log}_b(x)\) pamoja na kuhama,\(g(x)={\log}_b(x)+d\) na kuhama chini,\(h(x)={\log}_b(x)−d\) .Angalia Kielelezo\(\PageIndex{10}\).
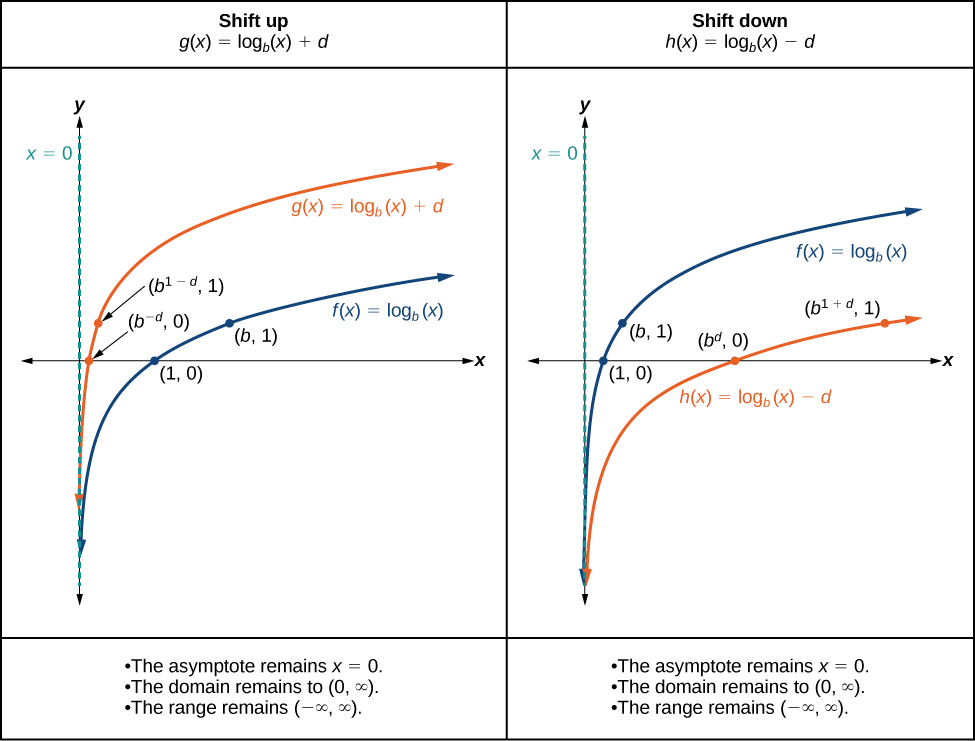
Kwa mara kwa mara yoyote\(d\), kazi\(f(x)={\log}_b(x)+d\)
- mabadiliko mzazi kazi\(y={\log}_b(x)\) up\(d\) vitengo kama\(d>0\).
- mabadiliko mzazi kazi\(y={\log}_b(x)\) chini\(d\) vitengo kama\(d<0\).
- ina asymptote ya wima\(x=0\).
- ina uwanja\((0,\infty)\).
- ina mbalimbali\((−\infty,\infty)\).
- Tambua mabadiliko ya wima:
- Kama\(d>0\), kuhama grafu ya\(d\) vitengo\(f(x)={\log}_b(x)\) up.
- Ikiwa\(d<0\), ongeza grafu ya\(d\) vitengo vya\(f(x)={\log}_b(x)\) chini.
- Chora asymptote ya wima\(x=0\).
- Tambua pointi tatu muhimu kutoka kwa kazi ya mzazi. Pata kuratibu mpya kwa kazi zilizobadilishwa\(d\) kwa kuongeza\(y\) kuratibu.
- Lebo pointi tatu.
- Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Mchoro grafu ya\(f(x)={\log}_3(x)−2\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptote kwenye grafu. Weka kikoa, upeo, na asymptote.
Suluhisho
Tangu kazi ni\(f(x)={\log}_3(x)−2\), tutaona\(d=–2\). Hivyo\(d<0\).
Hii ina maana sisi kuhama kazi\(f(x)={\log}_3(x)\) chini\(2\) vitengo.
Asymptote ya wima ni\(x=0\).
Fikiria pointi tatu muhimu kutoka kwa kazi ya mzazi\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), na\((3,1)\).
Kuratibu mpya hupatikana kwa kuondoa\(2\) kutoka kwa kuratibu y.
Weka alama\(\left(\dfrac{1}{3},−3\right)\),\((1,−2)\), na\((3,−1)\).
Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
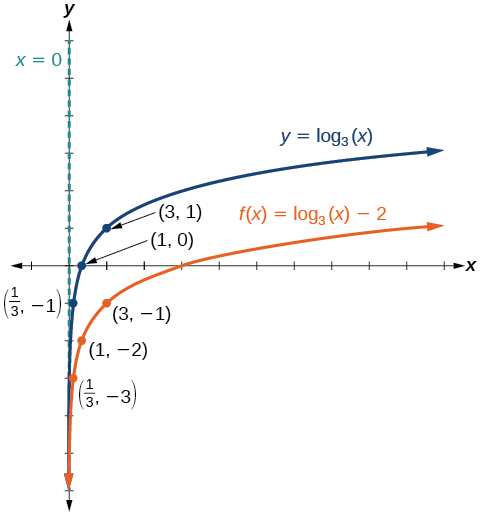
Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Mchoro grafu ya\(f(x)={\log}_2(x)+2\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptote kwenye grafu. Weka kikoa, upeo, na asymptote.
- Jibu
-
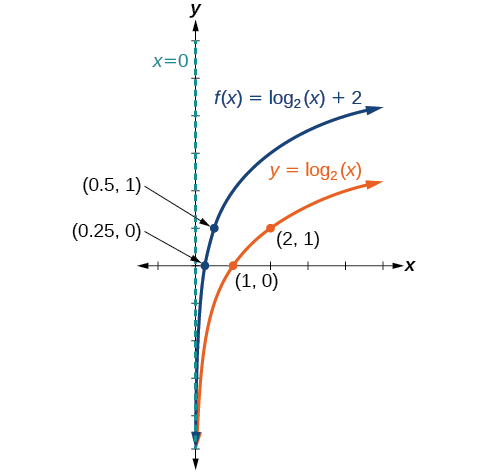
Kielelezo\(\PageIndex{12}\) Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Graphing Stretches na compressions ya\(y = log_b(x)\)
Wakati kazi ya mzazi\(f(x)={\log}_b(x)\) imeongezeka kwa mara kwa mara\(a>0\), matokeo ni kunyoosha wima au ukandamizaji wa grafu ya awali. Ili kutazama stretches na compressions, sisi kuweka\(a>1\) na kuchunguza grafu ya jumla ya kazi mzazi\(f(x)={\log}_b(x)\) pamoja kunyoosha wima,\(g(x)=a{\log}_b(x)\) na compression wima,\(h(x)=\dfrac{1}{a}{\log}_b(x)\) .Angalia Kielelezo\(\PageIndex{13}\).
Kwa mara kwa mara yoyote\(a>1\), kazi\(f(x)=a{\log}_b(x)\)
- stretches kazi mzazi\(y={\log}_b(x)\) wima kwa sababu ya\(a\) kama\(a>1\).
- compresses kazi mzazi\(y={\log}_b(x)\) wima kwa sababu ya\(a\) kama\(0<a<1\).
- ina asymptote ya wima\(x=0\).
- ina\(x\) -intercept\((1,0)\).
- ina uwanja\((0,\infty)\).
- ina mbalimbali\((−\infty,\infty)\).
- Tambua kunyoosha wima au compressions:
- Ikiwa\(|a|>1\), grafu ya\(f(x)={\log}_b(x)\) imetambulishwa na sababu ya\(a\) vitengo.
- Ikiwa\(|a|<1\), grafu ya\(f(x)={\log}_b(x)\) imesisitizwa na sababu ya\(a\) vitengo.
- Chora asymptote ya wima\(x=0\).
- Tambua pointi tatu muhimu kutoka kwa kazi ya mzazi. Kupata kuratibu mpya kwa ajili ya kazi kubadilishwa kwa kuzidisha wao y kuratibu na\(a\).
- Lebo pointi tatu.
- Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Mchoro grafu ya\(f(x)=2{\log}_4(x)\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptote kwenye grafu. Weka kikoa, upeo, na asymptote.
Suluhisho
Tangu kazi ni\(f(x)=2{\log}_4(x)\), tutaona\(a=2\).
Hii ina maana sisi kunyoosha kazi\(f(x)={\log}_4(x)\) kwa sababu ya\(2\).
Asymptote ya wima ni\(x=0\).
Fikiria pointi tatu muhimu kutoka kwa kazi ya mzazi\(\left(\dfrac{1}{4},−1\right)\),\((1,0)\), na\((4,1)\).
Kuratibu mpya hupatikana kwa kuzidisha\(y\) kuratibu na\(2\).
Weka alama\(\left(\dfrac{1}{4},−2\right)\),\((1,0)\), na\((4,2)\).
Kikoa ni\((0, \infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\). Angalia Kielelezo\(\PageIndex{14}\).
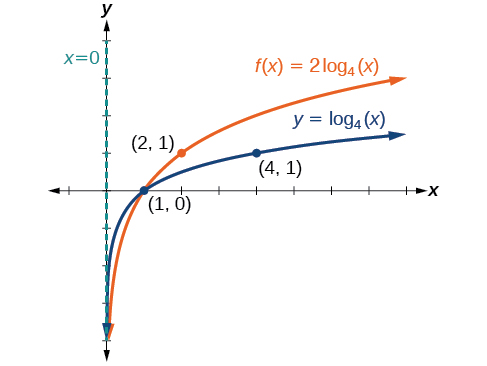
Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Mchoro grafu ya\(f(x)=\dfrac{1}{2}{\log}_4(x)\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptote kwenye grafu. Weka kikoa, upeo, na asymptote.
- Jibu
-
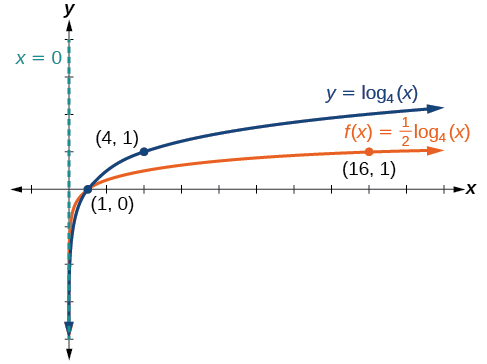
Kielelezo\(\PageIndex{15}\) Kikoa ni\((0,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Mchoro grafu ya\(f(x)=5{\log}(x+2)\). Weka kikoa, upeo, na asymptote.
Suluhisho
Kumbuka: kinachotokea ndani ya mabano hutokea kwanza. Kwanza, sisi hoja grafu kushoto\(2\) vitengo, kisha kunyoosha kazi wima kwa sababu ya\(5\), kama katika Kielelezo\(\PageIndex{16}\). Asymptote ya wima itabadilishwa\(x=−2\). \(x\)-Intercept itakuwa\((−1,0)\). Kikoa kitakuwa\((−2,\infty)\). Pointi mbili zitasaidia kutoa sura ya grafu:\((−1,0)\) na\((8,5)\). Tulichagua\(x=8\) kama kuratibu x ya hatua moja kwa grafu kwa sababu wakati\(x=8\),\(x+2=10\), msingi wa logarithm ya kawaida.
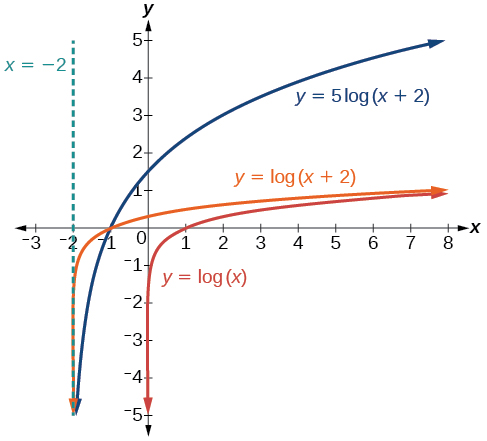
Kikoa ni\((−2,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=−2\).
Mchoro grafu ya kazi\(f(x)=3{\log}(x−2)+1\). Weka kikoa, upeo, na asymptote.
- Jibu
-
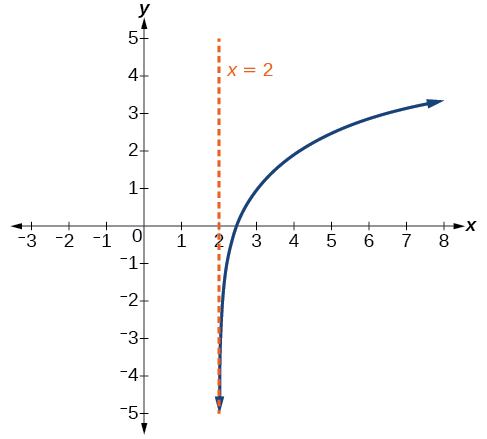
Kielelezo\(\PageIndex{17}\) Kikoa ni\((2,\infty)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=2\).
Graphing tafakari ya\(f(x) = log_b(x)\)
Wakati kazi ya mzazi\(f(x)={\log}_b(x)\) imeongezeka kwa\(−1\), matokeo ni kutafakari kuhusu\(x\) -axis. Wakati pembejeo imeongezeka na\(−1\), matokeo ni kutafakari kuhusu\(y\) -axis. Ili kutazama tafakari, tunazuia\(b>1\), na kuchunguza grafu ya jumla ya kazi ya mzazi\(f(x)={\log}_b(x)\) pamoja na kutafakari kuhusu\(x\) -axis,\(g(x)=−{\log}_b(x)\) na kutafakari kuhusu\(y\) -axis,\(h(x)={\log}_b(−x)\).
Kazi\(f(x)=−{\log}_b(x)\)
- huonyesha kazi ya mzazi\(y={\log}_b(x)\) kuhusu\(x\) -axis.
- ina uwanja,\((0,\infty)\), upeo\((−\infty,\infty)\), na asymptote wima\(x=0\), ambayo haibadilishwa kutoka kwa kazi ya mzazi.
Kazi\(f(x)={\log}_b(−x)\)
- huonyesha kazi ya mzazi\(y={\log}_b(x)\) kuhusu\(y\) -axis.
- ina uwanja\((−\infty,0)\).
- ina aina mbalimbali,\((−\infty,\infty)\), na asymptote ya wima\(x=0\), ambayo haibadilishwa kutoka kwa kazi ya mzazi.
| Kama\(f(x)=−{\log}_b(x)\) | Kama\(f(x)={\log}_b(−x)\) |
|---|---|
\ (f (x) ={\ logi} _b (x)\) ">
|
\ (f (x) = {\ logi} _b (-x)\) ">
|
\ (f (x) ={\ logi} _b (x)\) ">
|
\ (f (x) = {\ logi} _b (-x)\) ">
|
\ (f (x) ={\ logi} _b (x)\) ">
|
\ (f (x) = {\ logi} _b (-x)\) ">
|
\ (f (x) ={\ logi} _b (x)\) ">
|
\ (f (x) = {\ logi} _b (-x)\) ">
|
\ (f (x) ={\ logi} _b (x)\) ">
|
\ (f (x) = {\ logi} _b (-x)\) ">
|
Mchoro grafu ya\(f(x)=\log(−x)\) pamoja na kazi yake mzazi. Jumuisha pointi muhimu na asymptote kwenye grafu. Weka kikoa, upeo, na asymptote.
Suluhisho
Kabla ya kuchora\(f(x)=log(−x)\) picha\(f(x)=log(−x)\), kutambua tabia na pointi muhimu kwa grafu.
- Kwa kuwa\(b=10\) ni kubwa kuliko moja, tunajua kwamba kazi mzazi ni kuongezeka. Kwa kuwa thamani ya pembejeo imeongezeka kwa\(−1\),\(f(x)\) ni mfano wa grafu ya mzazi kuhusu\(y\) - mhimili. Hivyo,\(f(x)=\log(−x)\) itapungua kama\(x\) hatua kutoka infinity hasi hadi sifuri, na mkia wa kulia wa grafu utafikia asymptote wima\(x=0\).
- \(x\)Kizuizi ni\((−1,0)\).
- Tunapata na kuandika alama ya asymptote, njama na kuandika alama, na kuteka safu ya laini kupitia pointi.
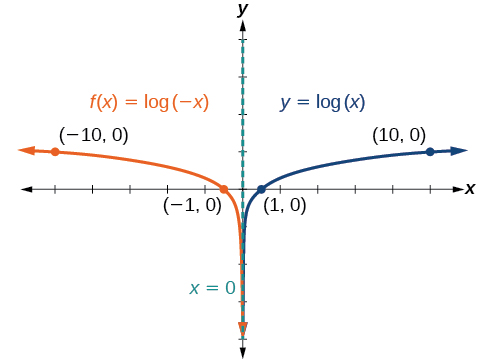
Kikoa ni\((−\infty,0)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
Grafu\(f(x)=−\log(−x)\). Weka kikoa, upeo, na asymptote.
- Jibu
-
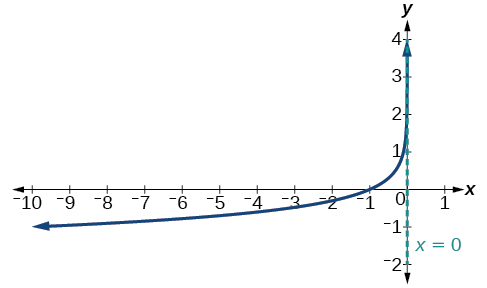
Kielelezo\(\PageIndex{20}\) Kikoa ni\((−\infty,0)\), upeo ni\((−\infty,\infty)\), na asymptote ya wima ni\(x=0\).
- Waandishi wa habari [Y=]. Ingiza equation ya logarithm au equations kama Y 1 = na, ikiwa inahitajika, Y 2 =.
- Waandishi wa habari [GRAPH] kuchunguza grafu za curves na utumie [WINDOW] ili kupata mtazamo sahihi wa grafu, ikiwa ni pamoja na hatua zao za makutano.
- Ili kupata thamani ya\(x\), sisi compute hatua ya makutano. Waandishi wa habari [2ND] kisha [CALC]. Chagua “intersect” na ubofye [ENTER] mara tatu. Hatua ya makutano inatoa thamani ya\(x\), kwa hatua (s) ya makutano.
Tatua\(4\ln(x)+1=−2\ln(x−1)\) graphically. Pande zote kwa elfu ya karibu.
Suluhisho
Bonyeza [Y=] na uingie\(4\ln(x)+1\) karibu na Y 1 =. Kisha ingiza\(−2\ln(x−1)\) karibu na Y 2 =. Kwa dirisha, tumia maadili kwa\(0\)\(x\0 and \(–10\) kwa\(5\)\(10\) ajili ya\(y\). Bonyeza [GRAPH]. Grafu zinapaswa kuingiliana mahali fulani kidogo na haki ya\(x=1\).
Kwa makadirio bora, vyombo vya habari [2ND] kisha [CALC]. Chagua [5: intersect] na waandishi wa habari [ENTER] mara tatu. Kuratibu x ya hatua ya makutano huonyeshwa kama\(1.3385297\). (Jibu lako inaweza kuwa tofauti kama unatumia dirisha tofauti au kutumia thamani tofauti kwa ajili ya Nadhani? ) Kwa hiyo, kwa elfu ya karibu,\(x≈1.339\).
Tatua\(5\log(x+2)=4−\log(x)\) graphically. Pande zote kwa elfu ya karibu.
- Jibu
-
\(x≈3.049\)
Kuhitimisha tafsiri za Kazi ya Logarithmic
Sasa kwa kuwa tumefanya kazi na kila aina ya tafsiri kwa kazi ya logarithmic, tunaweza muhtasari kila mmoja katika Jedwali\(\PageIndex{4}\) ili kufika equation ya jumla ya kutafsiri kazi za kielelezo.
| Tafsiri za Kazi ya Mzazi\(y={\log}_b(x)\) | |
|---|---|
| Tafsiri | Fomu |
| \ (y= {\ logi} _b (x)\) Tafsiri">
Shift \(c\)Vitengo vya usawa upande wa kushoto Vertikalt\(d\) vitengo up |
\ (y= {\ logi} _b (x)\) Fomu” style="wima align:middle; ">\(y={\log}_b(x+c)+d\) |
| \ (y= {\ logi} _b (x)\) Tafsiri">
Kunyoosha na Compress Kunyoosha kama\(|a|>1\) Ukandamizaji kama\(|a|<1\) |
\ (y= {\ logi} _b (x)\) Fomu” style="wima align:middle; ">\(y=a{\log}_b(x)\) |
| \ (y= {\ logi} _b (x)\) Tafsiri">Fikiria kuhusu x-axis | \ (y= {\ logi} _b (x)\) Fomu">\(y=−{\log}_b(x)\) |
| \ (y= {\ logi} _b (x)\) Tafsiri">Fikiria kuhusu mhimili wa y | \ (y= {\ logi} _b (x)\) Fomu">\(y={\log}_b(−x)\) |
| \ (y= {\ logi} _b (x)\) Tafsiri">Jumla equation kwa tafsiri zote | \ (y= {\ logi} _b (x)\) Fomu">\(y=a{\log}_b(x+c)+d\) |
Tafsiri zote za kazi ya mzazi logarithmic\(y={\log}_b(x)\),, na fomu
\(f(x)=a{\log}_b(x+c)+d\)
ambapo mzazi kazi\(y={\log}_b(x)\),\(b>1\), ni
- kubadilishwa vertikalt up\(d\) vitengo.
- kubadilishwa kwa usawa na\(c\) vitengo vya kushoto.
- aliweka wima kwa sababu ya\(|a|\) kama\(|a|>0\).
- USITUMIE vertically kwa sababu ya\(|a|\) kama\(0<|a|<1\).
- yalijitokeza kuhusu x- mhimili wakati\(a<0\).
Kwa\(f(x)=\log(−x)\), grafu ya kazi ya mzazi inaonekana kuhusu y -axis.
Asymptote ya wima ni\(f(x)=−2{\log}_3(x+4)+5\) nini?
Suluhisho
Asymptote ya wima iko\(x=−4\).
Uchambuzi
Mgawo, msingi, na tafsiri ya juu haiathiri asymptote. Mabadiliko ya\(4\) vitengo vya curve kwa mabadiliko ya kushoto asymptote wima kwa\(x=−4\).
Asymptote ya wima ni\(f(x)=3+\ln(x−1)\) nini?
- Jibu
-
\(x=1\)
Kupata equation inawezekana kwa ajili ya kazi ya kawaida logarithmic graphed katika Kielelezo\(\PageIndex{21}\).
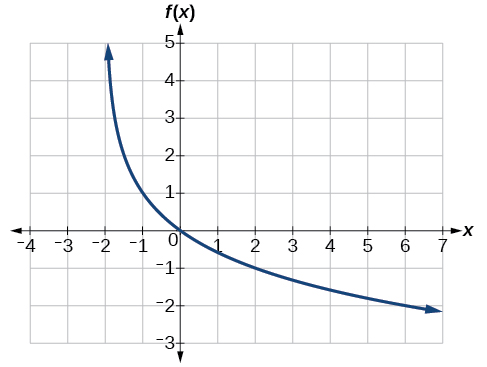
Suluhisho
Grafu hii ina asymptote ya wima\(x=–2\) na imeonekana kwa wima. Hatujui bado mabadiliko ya wima au kunyoosha wima. Tunajua hadi sasa kwamba equation itakuwa na fomu:
\(f(x)=−a\log(x+2)+k\)
Inaonekana grafu inapita kupitia pointi\((–1,1)\) na\((2,–1)\). Kubadilisha\((–1,1)\),
\[\begin{align*} 1&= -a\log(-1+2)+k \qquad \text{Substitute} (-1,1)\\ 1&= -a\log(1)+k \qquad \text{Arithmetic}\\ 1&= k\log(1)\\ &= 0 \end{align*}\]
Next, badala katika\((2,–1)\),
\[\begin{align*} -1&= -a\log(2+2)+1 \qquad \text{Substitute} (2,-1)\\ -2&= -a\log(4) \qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} \qquad \text{Solve for a} \end{align*}\]
Hii inatupa equation\(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\).
Uchambuzi
Tunaweza kuthibitisha jibu hili kwa kulinganisha maadili ya kazi katika Jedwali\(\PageIndex{5}\) na pointi kwenye grafu katika Kielelezo\(\PageIndex{21}\).
| \(x\) | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(f(x)\) | 1 | 0 | -0.58496 | -1 | -1.3219 |
| \(x\) | 4 | 5 | 6 | 7 | 8 |
| \(f(x)\) | -1.5850 | -1.8074 | -2 | -2.1699 | -2.3219 |
Kutoa equation ya logarithm asili graphed katika Kielelezo\(\PageIndex{22}\).
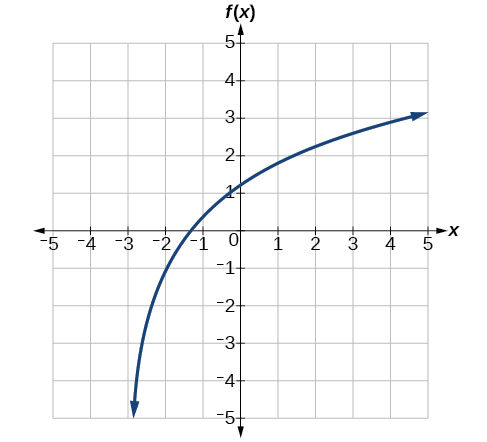
- Jibu
-
\(f(x)=2\ln(x+3)−1\)
Vyombo
Ndiyo, ikiwa tunajua kazi ni kazi ya jumla ya logarithmic. Kwa mfano, angalia grafu katika Kielelezo\(\PageIndex{22}\). Grafu inakaribia\(x=−3\) (au karibu) kwa karibu zaidi na zaidi, hivyo\(x=−3\) ni, au ni karibu sana, asymptote ya wima. Inakaribia kutoka kulia, hivyo uwanja ni pointi zote kwa haki,\({x|x>−3}\). Aina, kama ilivyo na kazi zote za jumla za logarithmic, ni namba zote halisi. Na tunaweza kuona tabia ya mwisho kwa sababu graph huenda chini kama unaendelea kushoto na juu kama unaendelea haki. tabia ya mwisho ni kwamba kama\(x\rightarrow −3^+\),\(f(x)\rightarrow −\infty\) na kama\(x\rightarrow \infty\),\(f(x)\rightarrow \infty\).
Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na logarithms ya graphing.
- Graph Kazi ya Kielelezo na Kazi ya Logarithmic
- Mchoro wa Mechi na Kazi za Kielelezo na za Logarithmic
- Pata Domain ya Kazi za Logarithmic
Mlinganyo muhimu
| Fomu ya jumla ya Tafsiri ya Kazi ya Logarithmic ya Mzazi\(f(x)={\log}_b(x)\) | \(f(x)=a{\log}_b(x+c)+d\) |
Dhana muhimu
- Ili kupata uwanja wa kazi ya logarithmic, kuanzisha usawa kuonyesha hoja kubwa kuliko sifuri, na kutatua\(x\). Angalia Mfano\(\PageIndex{1}\) na Mfano\(\PageIndex{2}\)
- Grafu ya kazi ya mzazi\(f(x)={\log}_b(x)\) ina x- intercept katika\((1,0)\), uwanja,\((0,\infty)\) upeo\((−\infty,\infty)\), asymptote wima\(x=0\), na
-
- ikiwa\(b>1\), kazi inaongezeka.
- ikiwa\(0<b<1\), kazi inapungua.
- Equation\(f(x)={\log}_b(x+c)\) hubadilisha kazi ya mzazi\(y={\log}_b(x)\) kwa usawa
- kushoto\(c\) vitengo kama\(c>0\).
- \(c\)vitengo haki kama\(c<0\).
- Equation\(f(x)={\log}_b(x)+d\) hubadilisha kazi ya mzazi\(y={\log}_b(x)\) kwa wima
- up\(d\) vitengo kama\(d>0\).
- chini\(d\) vitengo kama\(d<0\).
- Kwa mara kwa mara yoyote\(a>0\), equation\(f(x)=a{\log}_b(x)\)
- stretches kazi mzazi\(y={\log}_b(x)\) wima kwa sababu ya\(a\) kama\(|a|>1\).
- compresses kazi mzazi\(y={\log}_b(x)\) wima kwa sababu ya\(a\) kama\(|a|<\) 1.
- Wakati kazi ya mzazi\(y={\log}_b(x)\) imeongezeka kwa\(−1\), matokeo ni kutafakari kuhusu x -axis. Wakati pembejeo imeongezeka kwa\(−1\), matokeo ni kutafakari kuhusu y -axis.
- Equation\(f(x)=−{\log}_b(x)\) inawakilisha kutafakari kazi ya mzazi kuhusu x- axis.
- Equation\(f(x)={\log}_b(−x)\) inawakilisha kutafakari kazi ya mzazi kuhusu y- axis.
- Calculator graphing inaweza kutumika kwa takriban ufumbuzi wa baadhi equations logarithmic Angalia Mfano\(\PageIndex{9}\).
- Tafsiri zote za kazi ya logarithmic zinaweza kufupishwa kwa usawa wa jumla\(f(x)=a{\log}_b(x+c)+d\). Angalia Jedwali\(\PageIndex{4}\).
- Kutokana na equation na fomu ya jumla\(f(x)=a{\log}_b(x+c)+d\), tunaweza kutambua asymptote wima\(x=−c\) kwa mabadiliko. Angalia Mfano\(\PageIndex{10}\).
- Kutumia equation ya jumla\(f(x)=a{\log}_b(x+c)+d\), tunaweza kuandika equation ya kazi logarithmic kutokana na grafu yake. Angalia Mfano\(\PageIndex{11}\).


