5.9: Mfano Kutumia Tofauti

Last updated
Save as PDF

Page ID: 180837

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Katika sehemu hii, utakuwa:

Tatua matatizo ya tofauti ya moja kwa moja.
Tatua matatizo ya tofauti ya kinyume.
Tatua matatizo yanayohusisha tofauti ya pamoja.

Kampuni iliyotumiwa ya gari imetoa tu mgombea wao bora, Nicole, nafasi katika mauzo. nafasi inatoa 16% tume ya mauzo yake. Mapato yake yanategemea kiasi cha mauzo yake. Kwa mfano, kama anauza gari kwa $4,600, atapata $736. Anataka kutathmini kutoa, lakini hajui jinsi gani. Katika sehemu hii, tutaangalia mahusiano, kama hii, kati ya mapato, mauzo, na kiwango cha tume.

Kutatua matatizo ya Tofauti ya moja kwa moja

Katika mfano hapo juu, mapato ya Nicole yanaweza kupatikana kwa kuzidisha mauzo yake kwa tume yake. Fomu$e=0.16s$ hiyo inatuambia mapato yake$e$, kuja kutoka kwa bidhaa ya 0.16, tume yake, na bei ya kuuza ya gari. Ikiwa tunaunda meza, tunaona kwamba kama bei ya mauzo inavyoongezeka, mapato yanaongezeka pia, ambayo inapaswa kuwa intuitive. Angalia Jedwali 5.8.1.

$s$, bei ya mauzo	$e=0.16s$	Ukalimani
\ (s\), bei ya mauzo” class="lt-math-1351">$9,200	\ (e=0.16s\)” class="lt-math-1351">$e=0.16(9,200)=1,472$	Uuzaji wa gari la $9,200 husababisha mapato ya $1472.
\ (s\), bei ya mauzo” class="lt-math-1351">$4,600	\ (e=0.16s\)” class="lt-math-1351">$e=0.16(4,600)=736$	Uuzaji wa gari la $4,600 husababisha mapato ya $736.
\ (s\), bei ya mauzo” class="lt-math-1351">$18,400	\ (e=0.16s\)” class="lt-math-1351">$e=0.16(18,400)=2,944$	mauzo ya $18,400 matokeo ya gari katika $2944 mapato.

Jedwali 5.8.1

Kumbuka kwamba mapato ni nyingi ya mauzo. Kama ongezeko la mauzo, mapato huongezeka kwa njia inayoweza kutabirika. Mara mbili ya mauzo ya gari kutoka $4,600 kwa $9,200, na sisi mara mbili ya mapato kutoka $736 kwa $1,472. Kama pembejeo inapoongezeka, pato huongezeka kama nyingi za pembejeo. Uhusiano ambao kiasi kimoja ni mara kwa mara kinachoongezeka kwa kiasi kingine kinachoitwa tofauti ya moja kwa moja. Kila variable katika aina hii ya uhusiano inatofautiana moja kwa moja na nyingine.

Kielelezo 5.8.1 inawakilisha data kwa mapato ya uwezo wa Nicole. Tunasema kwamba mapato hutofautiana moja kwa moja na bei ya mauzo ya gari. Fomu$y=kx^n$ hutumiwa kwa tofauti ya moja kwa moja. Thamani$k$ ni mara kwa mara isiyo ya kawaida zaidi kuliko sifuri na inaitwa mara kwa mara ya tofauti. Katika kesi hii,$k=0.16$ na$n=1$. Tuliona kazi kama hii wakati tulijadili kazi za nguvu.

Kielelezo kina chanzo batili: picha inayoonekana mpaka kuokolewa... src=”/@api /deki/kurasa/ =Shelves%252FPreculus%252Fbook%253a_Precalculus_ (OpenStax) %252F 03% 25253A_Polynomial_and_Rational_functions%252F 3.9% 25253A_Modeling_Using_Variation/files/CNX_Precalc_Figure_03_09_001.jpg

Maelezo ya jumla: TOFAUTI YA DIRECT

Kama$x$ na$y$ ni kuhusiana na equation ya fomu

$y=kx^n$

basi sisi kusema kwamba uhusiano ni tofauti ya moja kwa moja na$y$ inatofautiana moja kwa moja na, au ni sawia na,$n$ th nguvu ya$x$. Katika mahusiano ya tofauti ya moja kwa moja, kuna uwiano wa mara kwa mara wa nonzero$k=\dfrac{y}{x^n}$, ambapo$k$ huitwa mara kwa mara ya tofauti, ambayo husaidia kufafanua uhusiano kati ya vigezo.

Kutokana na maelezo ya tatizo moja kwa moja tofauti, kutatua kwa haijulikani.

Tambua pembejeo$x$,, na pato,$y$.
Kuamua mara kwa mara ya tofauti. Unaweza kuhitaji kugawanya$y$ kwa nguvu maalum ya$x$ kuamua mara kwa mara ya tofauti.
Tumia mara kwa mara ya tofauti kuandika equation kwa uhusiano.
Mbadala inayojulikana maadili katika equation kupata haijulikani.

Mfano

Kutatua Tatizo la Tofauti ya moja kwa moja

kiasi$y$ inatofautiana moja kwa moja na mchemraba wa$x$. Kama$y=25$ wakati$x=2$, kupata$y$$x$ lini$6$.

Suluhisho

Fomu ya jumla ya tofauti ya moja kwa moja na mchemraba ni$y=kx^3$. Mara kwa mara inaweza kupatikana kwa kugawa$y$ na mchemraba wa$x$.

$k=\dfrac{y}{x^3}$

$=\dfrac{25}{2^3}$

$=\dfrac{25}{8}$

Sasa tumia mara kwa mara kuandika equation inayowakilisha uhusiano huu.

$y=\dfrac{25}{8}x^3$

Mbadala$x=6$ na kutatua kwa$y$.

$y=\dfrac{25}{8}{(6)}^3$

$=675$

Uchambuzi

Grafu ya equation hii ni cubic rahisi, kama inavyoonekana katika Kielelezo 5.8.2.

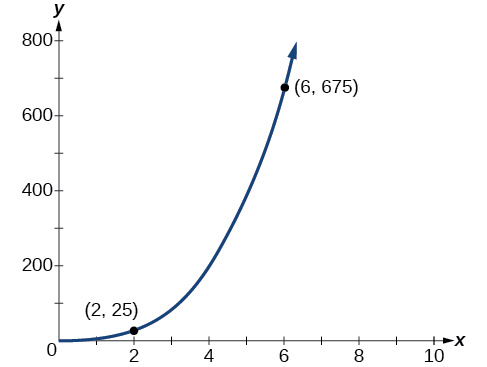
Grafu ya y=25/8 (x ^ 3) na alama zilizoandikwa (2, 25) na (6, 675). — Kielelezo 5.8.2

Q & A

Je! Grafu za equations zote za tofauti za moja kwa moja zinaonekana kama Mfano?

Hapana. Tofauti ya moja kwa moja milinganyo ni kazi za nguvu-zinaweza kuwa linear, quadratic, za ujazo, quartic, radical, nk Lakini grafu zote zinapita$(0,0)$.

Zoezi

Wingi$y$ hutofautiana moja kwa moja na mraba wa$x$. Kama$y=24$ wakati$x=3$, kupata$y$ lini$x$ ni 4.

Suluhisho

$\frac{128}{3}$

Kutatua Matatizo ya Tofauti ya Inverse

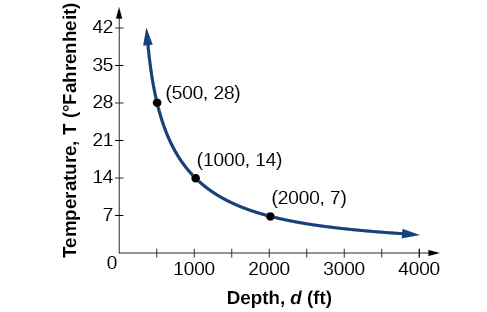
Joto la maji katika bahari linatofautiana kinyume na kina cha maji. Fomula$T=\frac{14,000}{d}$ inatupa halijoto katika digrii Fahrenheit kwa kina kwa miguu chini ya uso wa dunia. Fikiria Bahari ya Atlantiki, ambayo inashughulikia 22% ya uso wa Dunia. Katika eneo fulani, kwa kina cha futi 500, halijoto inaweza kuwa 28°F.

Ikiwa tunaunda Jedwali 5.8.2, tunaona kwamba, kama kina kinaongezeka, joto la maji hupungua.

$d$, kina	$T=\frac{14,000}{d}$	Ukalimani
\ (d\), kina” class="lt-math-1351">500 ft	\ (T=\ frac {14,000} {d}\)” class="lt-math-1351">$\frac{14,000}{500}=28$	Kwa kina cha ft 500 halijoto la maji ni 28° F.
\ (d\), kina” class="lt-math-1351">1000 ft	\ (T=\ frac {14,000} {d}\)” class="lt-math-1351">$\frac{14,000}{1000}=14$	Kwa kina cha ft 1,000 halijoto la maji ni 14° F.
\ (d\), kina” class="lt-math-1351">2000 ft	\ (T=\ frac {14,000} {d}\)” class="lt-math-1351">$\frac{14,000}{2000}=7$	Kwa kina cha ft 2,000 halijoto la maji ni 7° F.

Jedwali 5.8.2

Tunaona katika uhusiano kati ya vigezo hivi kwamba, kama kiasi kimoja kinaongezeka, nyingine hupungua. Wingi wawili wanasemekana kuwa inversely sawia na kila neno inatofautiana inversely na nyingine. Mahusiano ya uwiano wa kawaida pia huitwa tofauti tofauti.

Kwa mfano wetu, Mchoro 5.8.3 inaonyesha tofauti ya inverse. Tunasema joto la maji linatofautiana kinyume na kina cha maji kwa sababu, kama kina kinavyoongezeka, joto hupungua. Fomu$y=\frac{k}{x}$ ya tofauti ya inverse katika kesi hii inatumia$k=14,000$.

Grafu ya y= (14000) /x ambapo mhimili usio na usawa umeandikwa, “Kina, d (ft)”, na mhimili wima umeandikwa, “Joto, T (Degrees Fahrenheit)”. — Kielelezo 5.8.3

Kumbuka General: TOFAUTI INVERSE

Kama$x$ na$y$ ni kuhusiana na equation ya fomu

$y=\frac{k}{x^n}$

ambapo$k$ ni mara kwa mara nonzero, basi tunasema kwamba$y$ inatofautiana inversely na nguvu$n$ th ya$x$. Katika mahusiano yasiyo ya kawaida, au tofauti tofauti, kuna mara nyingi mara kwa mara$k=x^ny$.

Mfano

Kuandika Mfumo kwa Uhusiano wa Uwiano wa Inversely

utalii mipango ya kuendesha 100 maili. Pata formula kwa wakati safari itachukua kama kazi ya kasi ya anatoa utalii.

Suluhisho

Kumbuka kwamba kuzidisha kasi kwa wakati hutoa umbali. Ikiwa tunaruhusu$t$ kuwakilisha wakati wa gari kwa masaa, na$v$ kuwakilisha kasi (kasi au kiwango) ambacho watalii huendesha, basi$vt=$ umbali. Kwa sababu umbali ni fasta katika 100 maili,$vt=100$ hivyo$t=\frac{100}{v}$. Kwa sababu wakati ni kazi ya kasi, tunaweza kuandika$t(v)$.

$t(v)=\frac{100}{v}$

$=100v^{−1}$

Tunaweza kuona kwamba mara kwa mara ya tofauti ni 100 na, ingawa tunaweza kuandika uhusiano kwa kutumia exponent hasi, ni kawaida zaidi kuona imeandikwa kama sehemu. Tunasema kwamba wakati inatofautiana inversely na kasi.

Kutokana na maelezo ya tatizo moja kwa moja tofauti, kutatua kwa haijulikani.

Tambua pembejeo$x$,, na pato,$y$.
Kuamua mara kwa mara ya tofauti. Unaweza haja ya kuzidisha$y$ kwa nguvu maalum ya$x$ kuamua mara kwa mara ya tofauti.
Tumia mara kwa mara ya tofauti kuandika equation kwa uhusiano.
Mbadala inayojulikana maadili katika equation kupata haijulikani.

Mfano

Kutatua Tatizo la Tofauti ya Inverse

kiasi$y$ inatofautiana inversely na mchemraba wa$x$. Kama$y=25$ wakati$x=2$, kupata$y$$x$ lini$6$.

Suluhisho

Fomu ya jumla ya tofauti ya inverse na mchemraba ni$y=\frac{k}{x^3}$. Mara kwa mara inaweza kupatikana kwa kuzidisha$y$ na mchemraba wa$x$.

$k=x^3y$

$=2^3⋅25$

$=200$

Sasa tunatumia mara kwa mara kuandika equation ambayo inawakilisha uhusiano huu.

$y=\dfrac{k}{x^3}$,$ k=200$

$y=\dfrac{200}{x^3}$

Mbadala$x=6$ na kutatua kwa$y$.

$y=\dfrac{200}{6^3}$

$=\dfrac{25}{27}$

Uchambuzi

Grafu ya equation hii ni kazi ya busara, kama inavyoonekana kwenye Mchoro 5.8.4.

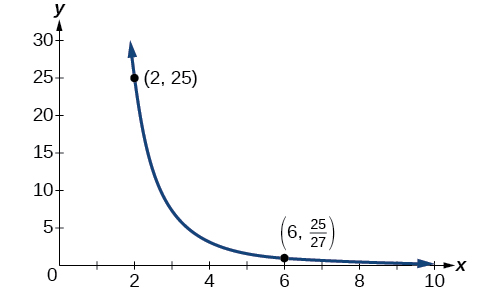
Grafu ya y=25/ (x ^ 3) na alama zilizoandikwa (2, 25) na (6, 25/27). — Kielelezo 5.8.4

Zoezi

kiasi$y$ inatofautiana inversely na mraba wa$x$. Kama$y=8$ wakati$x=3$, kupata$y$$x$ lini$4$.

Suluhisho

$\frac{9}{2}$

Kutatua Matatizo Kuhusisha Tofauti ya Pamoja

Hali nyingi ni ngumu zaidi kuliko tofauti ya msingi ya moja kwa moja au mfano wa tofauti. Variable moja mara nyingi inategemea vigezo vingine vingi. Wakati variable inategemea bidhaa au quotient ya vigezo mbili au zaidi, hii inaitwa tofauti ya pamoja. Kwa mfano, gharama ya kuhudhuria wanafunzi kwa kila safari ya shule inatofautiana na idadi ya wanafunzi wanaohudhuria na umbali kutoka shule. Variable$c$, gharama, inatofautiana pamoja na idadi ya wanafunzi$n$,, na umbali,$d$.

Maelezo ya jumla: TOFAUTI YA PAMOJA

Tofauti ya pamoja hutokea wakati variable inatofautiana moja kwa moja au inversely na vigezo mbalimbali.

Kwa mfano, kama$x$ inatofautiana moja kwa moja na wote$y$ na$z$, tuna$x=kyz$. Kama$x$ inatofautiana moja kwa moja$y$ na na inversely kwa$z$, tuna$x=\frac{ky}{z}$. Kumbuka kwamba sisi tu kutumia mara kwa mara moja katika pamoja tofauti equation.

Mfano

Kutatua Matatizo Kuhusisha Tofauti ya Pamoja

kiasi$x$ inatofautiana moja kwa moja na mraba wa$y$ na inversely na mizizi mchemraba wa$z$. Kama$x=6$ wakati$y=2$ na$z=8$, kupata$x$ lini$y=1$ na$z=27$.

Suluhisho

Anza kwa kuandika equation kuonyesha uhusiano kati ya vigezo.

$x=\dfrac{ky^2}{\sqrt[3]{z}}$

Mbadala$x=6$$y=2$,, na$z=8$ kupata thamani ya mara kwa mara$k$.

$6=\dfrac{k2^2}{\sqrt[3]{8}}$

$6=\dfrac{4k}{2}$

$3=k$

Sasa tunaweza kubadilisha thamani ya mara kwa mara katika equation kwa uhusiano.

$x=\dfrac{3y^2}{\sqrt[3]{z}}$

Ili kupata$x$ wakati$y=1$ na$z=27$, sisi mbadala maadili kwa$y$ na$z$ katika equation yetu.

$x=\dfrac{3{(1)}^2}{\sqrt[3]{27}}$

$=1$

Zoezi

kiasi$x$ inatofautiana moja kwa moja na mraba wa$y$ na inversely na$z$. Kama$x=40$ wakati$y=4$ na$z=2$, kupata$x$ lini$y=10$ na$z=25$.

Suluhisho

$x=20$

vyombo vya habari

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na tofauti ya moja kwa moja na inverse.

Ziara tovuti hii kwa maswali ya ziada mazoezi kutoka Learningpod.

Mlinganyo muhimu

Tofauti ya moja kwa moja	$y=kx^n$,$k$ ni mara kwa mara ya nonzero.
Tofauti ya kinyume	$y=\dfrac{k}{x^n}$,$k$ ni mara kwa mara ya nonzero.

Dhana muhimu

Uhusiano ambapo kiasi kimoja ni mara kwa mara kinachoongezeka kwa wingi mwingine huitwa tofauti moja kwa moja. Angalia Mfano.
Vigezo viwili ambavyo ni sawa sawa na kila mmoja vitakuwa na uwiano wa mara kwa mara.
Uhusiano ambapo kiasi kimoja ni mara kwa mara kilichogawanywa na kiasi kingine kinachoitwa tofauti tofauti. Angalia Mfano.
Vigezo viwili ambavyo ni inversely sawia na mtu mwingine vitakuwa na mara nyingi mara kwa mara. Angalia Mfano.
Katika matatizo mengi, variable inatofautiana moja kwa moja au inversely na vigezo mbalimbali. Tunaita aina hii ya tofauti ya uhusiano wa pamoja. Angalia Mfano.

\(s\), bei ya mauzo	\(e=0.16s\)	Ukalimani
\ (s\), bei ya mauzo” class="lt-math-1351">$9,200	\ (e=0.16s\)” class="lt-math-1351">\(e=0.16(9,200)=1,472\)	Uuzaji wa gari la $9,200 husababisha mapato ya $1472.
\ (s\), bei ya mauzo” class="lt-math-1351">$4,600	\ (e=0.16s\)” class="lt-math-1351">\(e=0.16(4,600)=736\)	Uuzaji wa gari la $4,600 husababisha mapato ya $736.
\ (s\), bei ya mauzo” class="lt-math-1351">$18,400	\ (e=0.16s\)” class="lt-math-1351">\(e=0.16(18,400)=2,944\)	mauzo ya $18,400 matokeo ya gari katika $2944 mapato.

Tofauti ya moja kwa moja	\(y=kx^n\),\(k\) ni mara kwa mara ya nonzero.
Tofauti ya kinyume	\(y=\dfrac{k}{x^n}\),\(k\) ni mara kwa mara ya nonzero.