11.3: Utaratibu wa kijiometri

Last updated
Save as PDF

Page ID: 181166

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Pata uwiano wa kawaida kwa mlolongo wa kijiometri.
Andika orodha ya mlolongo wa kijiometri.
Tumia formula ya kujirudia kwa mlolongo wa kijiometri.
Tumia formula wazi kwa mlolongo wa kijiometri.

Kazi nyingi hutoa ongezeko la kila mwaka la gharama za maisha ili kuweka mishahara sambamba na mfumuko wa bei. Tuseme, kwa mfano, mhitimu wa chuo cha hivi karibuni hupata nafasi kama meneja wa mauzo kupata mshahara wa kila mwaka wa$$26,000$. Anaahidi$2\%$ gharama za kuongezeka kwa maisha kila mwaka. Mshahara wake wa kila mwaka katika mwaka wowote unaweza kupatikana kwa kuzidisha mshahara wake kutoka mwaka uliopita na$102\%$. Mshahara wake utakuwa$$26,520$ baada ya mwaka mmoja;$$27,050.40$ baada ya miaka miwili,$$27,591.41$ baada ya miaka mitatu, na kadhalika. Wakati mshahara unaongezeka kwa kiwango cha mara kwa mara kila mwaka, mshahara unakua kwa sababu ya mara kwa mara. Katika sehemu hii, tutaangalia utaratibu unaokua kwa njia hii.

Kupata Uwiano wa kawaida

Maadili ya mshahara ya kila mwaka yaliyoelezwa huunda mlolongo wa kijiometri kwa sababu hubadilika kwa sababu ya mara kwa mara kila mwaka Kila neno la mlolongo wa kijiometri huongezeka au hupungua kwa sababu ya mara kwa mara inayoitwa uwiano wa kawaida. Mlolongo hapa chini ni mfano wa mlolongo wa kijiometri kwa sababu kila neno huongezeka kwa sababu ya mara kwa mara ya 6. Kuzidisha muda wowote wa mlolongo kwa uwiano wa kawaida 6 huzalisha muda unaofuata.

$Mlolongo, {1, 6, 36, 216, 1296,...} unaoonyesha namba zote zina uwiano wa kawaida wa 6.$

Ufafanuzi: SEKONDARI

Mlolongo wa kijiometri ni moja ambayo neno lolote lililogawanywa na muda uliopita ni mara kwa mara. Mara kwa mara hii inaitwa uwiano wa kawaida wa mlolongo. Uwiano wa kawaida unaweza kupatikana kwa kugawa neno lolote katika mlolongo kwa muda uliopita. Ikiwa$a_1$ ni muda wa awali wa mlolongo wa kijiometri na$r$ ni uwiano wa kawaida, mlolongo utakuwa

\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]

Jinsi ya: Kutokana na seti ya namba, onyesha ikiwa zinawakilisha mlolongo wa kijiometri.

Gawanya kila neno kwa muda uliopita.
Linganisha quotients. Ikiwa ni sawa, uwiano wa kawaida upo na mlolongo ni kijiometri.

Mfano$\PageIndex{1}$: Finding Common Ratios

Je, mlolongo wa kijiometri? Ikiwa ndivyo, pata uwiano wa kawaida.

$1$,$2$,$4$,$8$,$16$,...
$48$,$12$,$4$,$2$,...

Suluhisho

Gawanya kila neno kwa muda uliopita ili uone kama uwiano wa kawaida upo.

$\dfrac{2}{1}=2$$\dfrac{4}{2}=2$$\dfrac{8}{4}=2$$\dfrac{16}{8}=2$
Mlolongo ni kijiometri kwa sababu kuna uwiano wa kawaida. Uwiano wa kawaida ni$2$.
$\dfrac{12}{48}=\dfrac{1}{4}$$\dfrac{4}{12}=\dfrac{1}{3}$$\dfrac{2}{4}=\dfrac{1}{2}$
Mlolongo sio kijiometri kwa sababu hakuna uwiano wa kawaida.

Uchambuzi

Grafu ya kila mlolongo inavyoonekana kwenye Kielelezo$\PageIndex{1}$. Inaonekana kutoka kwenye grafu ambazo zote (a) na (b) zinaonekana zina fomu ya grafu ya kazi ya kielelezo katika dirisha hili la kutazama. Hata hivyo, tunajua kwamba (a) ni kijiometri na hivyo tafsiri hii inashikilia, lakini (b) sio.

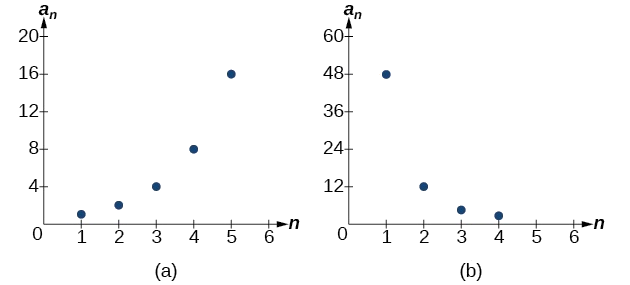
$Grafu ya utaratibu mbili ambapo grafu (a) ni kijiometri na grafu (b) ni kielelezo.$

Kielelezo$\PageIndex{1}$

Q & A

Ikiwa unaambiwa kuwa mlolongo ni kijiometri, unapaswa kugawanya kila neno kwa muda uliopita ili kupata uwiano wa kawaida?

Hapana. Ikiwa unajua kwamba mlolongo ni kijiometri, unaweza kuchagua neno lolote katika mlolongo na ugawanye kwa muda uliopita ili kupata uwiano wa kawaida.

Zoezi$\PageIndex{1A}$

Je, mlolongo wa kijiometri? Ikiwa ndivyo, pata uwiano wa kawaida.

$5$,$10$,$15$,$20$,...

Jibu: Mlolongo sio kijiometri kwa sababu$\dfrac{10}{5}≠\dfrac{15}{10}$

Zoezi$\PageIndex{1B}$

Je, mlolongo wa kijiometri? Ikiwa ndivyo, pata uwiano wa kawaida.

$100$,$20$,$4$,$\dfrac{4}{5}$,...

Jibu: Mlolongo ni kijiometri. Uwiano wa kawaida ni$\dfrac{1}{5}$

Kuandika Masharti ya Utaratibu wa Jiometri

Sasa kwa kuwa tunaweza kutambua mlolongo wa kijiometri, tutajifunza jinsi ya kupata maneno ya mlolongo wa kijiometri ikiwa tunapewa muda wa kwanza na uwiano wa kawaida. Masharti ya mlolongo wa kijiometri yanaweza kupatikana kwa kuanzia na muda wa kwanza na kuongezeka kwa uwiano wa kawaida mara kwa mara. Kwa mfano, kama muda wa kwanza wa mlolongo kijiometri ni$a_1=−2$ na uwiano wa kawaida ni$r=4$, tunaweza kupata masharti baadae kwa$−2⋅4$ kuzidisha kupata$−8$ kisha$−8⋅4$ kuzidisha matokeo ya kupata$−32$ na kadhalika.

\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]

Masharti manne ya kwanza ni$\{–2, –8, –32, –128\}$.

Jinsi ya: Kutokana na muda wa kwanza na jambo la kawaida, pata masharti manne ya kwanza ya mlolongo wa kijiometri.

Kuzidisha muda wa awali$a_1$,, kwa uwiano wa kawaida ili kupata muda ujao,$a_2$.
Kurudia mchakato, ukitumia$a_n=a_2$ kupata$a_3$ na kisha utumie$a_3$ kupata$a_4$, mpaka maneno yote manne yametambuliwa.
Andika maneno yaliyotengwa na commons ndani ya mabano.

Mfano$\PageIndex{2}$: Writing the Terms of a Geometric Sequence

Andika orodha nne za kwanza za mlolongo wa kijiometri$a_1=5$ na$r=–2$.

Suluhisho

$a_1$$−2$Kuzidisha na kupata$a_2$. Kurudia mchakato, ukitumia$a_2$ kupata$a_3$, na kadhalika.

\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]

Masharti manne ya kwanza ni$\{5,–10,20,–40\}$.

Zoezi$\PageIndex{2}$

Andika orodha tano za kwanza za mlolongo wa kijiometri$a_1=18$ na$r=\dfrac{1}{3}$.

Jibu: $\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} $

Kutumia Fomu za Kurudia kwa Utaratibu wa kijiomet

Fomu ya kujirudia inatuwezesha kupata muda wowote wa mlolongo wa kijiometri kwa kutumia muda uliopita. Kila neno ni bidhaa ya uwiano wa kawaida na muda uliopita. Kwa mfano, tuseme uwiano wa kawaida ni$9$. Kisha kila neno ni mara tisa ya muda uliopita. Kama ilivyo kwa formula yoyote ya kujirudia, muda wa awali unapaswa kupewa.

Kumbuka: formula ya kujirudia kwa mlolongo wa kijiometri

formula kujirudia kwa mlolongo kijiometri na uwiano wa kawaida r na muda$a_1$ wa kwanza ni

\[a_n=ra_{n−1},\;\;\; n≥2\]

Jinsi ya: Kutokana na masharti kadhaa ya kwanza ya mlolongo wa kijiometri, andika formula yake ya kujirudia.

Hali ya muda wa awali.
Pata uwiano wa kawaida kwa kugawa neno lolote kwa muda uliotangulia.
Badilisha uwiano wa kawaida katika formula ya kujirudia kwa mlolongo wa kijiometri.

Mfano$\PageIndex{3}$: Using Recursive Formulas for Geometric Sequences

Andika formula ya kujirudia kwa mlolongo wa kijiometri wafuatayo.

$\{6, 9, 13.5, 20.25, ...\} \nonumber$

Suluhisho

Neno la kwanza linapewa kama$6$. Uwiano wa kawaida unaweza kupatikana kwa kugawa muda wa pili kwa muda wa kwanza.

$r=\dfrac{9}{6}=1.5 \nonumber$

Badilisha uwiano wa kawaida katika formula ya kujirudia kwa utaratibu wa kijiometri na ufafanue$a_1$.

\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]

Uchambuzi

Mlolongo wa pointi za data hufuata mfano wa kielelezo. uwiano wa kawaida pia ni msingi wa kazi kielelezo kama inavyoonekana katika Kielelezo$\PageIndex{2}$.

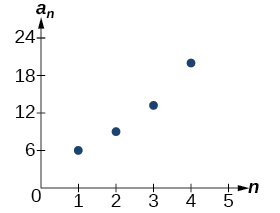
$Grafu ya mlolongo wa kijiometri.$

Kielelezo$\PageIndex{2}$

Q & A

Je, tunapaswa kugawanya muda wa pili kwa muda wa kwanza ili kupata uwiano wa kawaida?

Hapana. Tunaweza kugawanya muda wowote katika mlolongo kwa muda uliopita. Hata hivyo, ni kawaida kugawanya muda wa pili kwa muda wa kwanza kwa sababu mara nyingi ni njia rahisi ya kupata uwiano wa kawaida.

Zoezi$\PageIndex{3}$

Andika formula ya kujirudia kwa mlolongo wa kijiometri wafuatayo.

$\{2, 43, 89, 1627, ...\}$

Jibu: $\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}$

Kutumia Fomu wazi kwa Utaratibu wa kijiometri

Kwa sababu mlolongo wa kijiometri ni kazi ya kielelezo ambao uwanja wake ni seti ya integers nzuri, na uwiano wa kawaida ni msingi wa kazi, tunaweza kuandika formula wazi ambayo inaruhusu sisi kupata maneno fulani.

\[a_n=a_1r^{n−1}\]

Hebu tuangalie mlolongo$\{18, 36, 72, 144, 288, ...\}$. Hii ni mlolongo wa kijiometri$2$ na uwiano wa kawaida wa na kazi kielelezo na msingi wa$2$. Fomu wazi kwa mlolongo huu ni

$a_n=18·2^{n−1}$

Grafu ya mlolongo imeonyeshwa kwenye Kielelezo$\PageIndex{3}$.

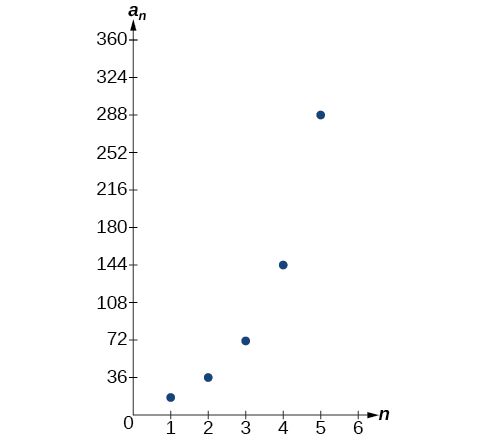
$Grafu ya mlolongo wa kijiometri.$

Kielelezo$\PageIndex{3}$

Kumbuka: FORMULA YA WAZI KWA MLOLONGO WA KIJI

$n^{th}$Neno la mlolongo wa kijiometri hutolewa na formula wazi:

\[a_n=a_1r^{n−1}\]

Mfano$\PageIndex{4}$: Writing Terms of Geometric Sequences Using the Explicit Formula

Kutokana na mlolongo wa kijiometri$a_1=3$ na$a_4=24$, tafuta$a_2$.

Suluhisho

Mlolongo unaweza kuandikwa kwa suala la muda wa awali na uwiano wa kawaida$r$.

$3$,$3r$,$3r^2$,$3r^3$,...

Pata uwiano wa kawaida kwa kutumia muda uliopewa nne.

\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]

Pata muda wa pili kwa kuzidisha muda wa kwanza kwa uwiano wa kawaida.

\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]

Uchambuzi

Uwiano wa kawaida huongezeka kwa muda wa kwanza mara moja ili kupata muda wa pili, mara mbili kupata muda wa tatu, mara tatu kupata muda wa nne, na kadhalika. Neno la kumi linaweza kupatikana kwa kuzidisha muda wa kwanza kwa uwiano wa kawaida mara tisa au kwa kuzidisha kwa uwiano wa kawaida uliofufuliwa hadi nguvu ya tisa.

Zoezi$\PageIndex{4}$

Kutokana na mlolongo wa kijiometri$a_2=4$ na$2a_3=32$, tafuta$a_6$.

Jibu: $a_6=16,384$

Mfano$\PageIndex{5}$: Writing an Explicit Formula for the nth Term of a Geometric Sequence

Andika formula wazi kwa muda wa nth wa mlolongo wa kijiometri wafuatayo.

$\{2, 10, 50, 250, ...\}$

Suluhisho

Muda wa kwanza ni$2$. Uwiano wa kawaida unaweza kupatikana kwa kugawa muda wa pili kwa muda wa kwanza.

$\dfrac{10}{2}=5$

Uwiano wa kawaida ni$5$. Weka uwiano wa kawaida na muda wa kwanza wa mlolongo katika formula.

\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]

Grafu ya mlolongo huu katika Kielelezo$\PageIndex{4}$ inaonyesha muundo wa kielelezo.

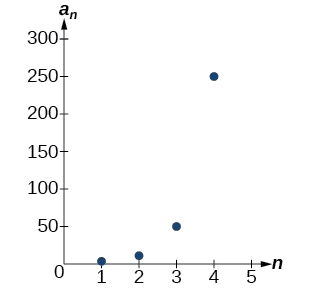
$Grafu ya mlolongo wa kijiometri.$

Kielelezo$\PageIndex{4}$

Zoezi$\PageIndex{5}$

Andika formula wazi kwa mlolongo wa kijiometri wafuatayo.

$\{–1, 3, –9, 27, ...\}$

Jibu: $a_n=−{(−3)}^{n−1}$

Kutatua Matatizo ya Maombi na Utaratibu wa Kiji

Katika matukio halisi ya ulimwengu yanayohusisha utaratibu wa hesabu, tunaweza kuhitaji kutumia neno la awali la$a_0$ badala ya$a_1$. Katika matatizo haya, tunaweza kubadilisha formula wazi kidogo kwa kutumia formula ifuatayo:

$a_n=a_0r^n$

Mfano$\PageIndex{6}$: Solving Application Problems with Geometric Sequences

Mwaka 2013, idadi ya wanafunzi katika shule ndogo ni$284$. Inakadiriwa kuwa idadi ya wanafunzi itaongezeka kwa$4\%$ kila mwaka.

Andika formula kwa idadi ya wanafunzi.
Tathmini idadi ya wanafunzi mwaka 2020.

Suluhisho

Hali inaweza kuelekezwa na mlolongo wa kijiometri na muda wa awali wa$284$. Idadi ya wanafunzi itakuwa$104\%$ ya mwaka kabla, hivyo uwiano wa kawaida ni$1.04$.
Hebu$P$ kuwa idadi ya wanafunzi na$n$ kuwa idadi ya miaka baada ya 2013. Kutumia formula wazi kwa mlolongo wa kijiometri tunayopata

$P_n =284⋅{1.04}^n$
Tunaweza kupata idadi ya miaka tangu 2013 kwa kutoa.
$2020−2013=7$

Tunatafuta idadi ya watu baada ya$7$ miaka. Tunaweza mbadala$7$ kwa ajili ya$n$ kukadiria idadi ya watu katika 2020.

$P_7=284⋅{1.04}^7≈374$

Idadi ya wanafunzi itakuwa karibu$374$ mwaka 2020.

Zoezi$\PageIndex{6}$

Biashara inaanza tovuti mpya. Awali idadi ya hits ni$293$ kutokana na sababu ya udadisi. Makadirio ya biashara ya idadi ya hits itaongezeka$2.6%$ kwa wiki.

Andika formula kwa idadi ya hits.
Tathmini idadi ya hits katika$5$ wiki.

Jibu: $P_n = 293⋅1.026a^n$
Jibu b: Idadi ya hits itakuwa karibu$333$.

Media

Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na utaratibu wa kijiometri.

Mlinganyo muhimu

formula ya kujirudia kwa muda wa nth wa mlolongo wa kijiometri	$a_n=ra_{n−1}$,$n≥2$
formula wazi kwa muda wa nth wa mlolongo wa kijiometri	$a_n=a_1r^{n−1}$

Dhana muhimu

Mlolongo wa kijiometri ni mlolongo ambao uwiano kati ya maneno yoyote mawili mfululizo ni mara kwa mara.
Uwiano wa mara kwa mara kati ya maneno mawili mfululizo huitwa uwiano wa kawaida.
Uwiano wa kawaida unaweza kupatikana kwa kugawa neno lolote katika mlolongo kwa muda uliopita. Angalia Mfano$\PageIndex{1}$.
Masharti ya mlolongo wa kijiometri yanaweza kupatikana kwa kuanzia na muda wa kwanza na kuongezeka kwa uwiano wa kawaida mara kwa mara. Angalia Mfano$\PageIndex{2}$ na Mfano$\PageIndex{4}$.
Fomu ya kujirudia kwa mlolongo wa kijiometri na uwiano wa kawaida$r$ hutolewa na$a_n=ra_{n–1}$ kwa$n≥2$.
Kama ilivyo kwa formula yoyote ya kujirudia, muda wa awali wa mlolongo lazima upewe. Angalia Mfano$\PageIndex{3}$.
Fomu ya wazi ya mlolongo wa kijiometri na uwiano wa kawaida$r$ hutolewa na$a_n=a_1r^{n–1}$. Angalia Mfano$\PageIndex{5}$.
Katika matatizo ya maombi, sisi wakati mwingine kubadilisha formula wazi kidogo kwa$a_n=a_0r^n$. Angalia Mfano$\PageIndex{6}$.

Wachangiaji na Majina

Template:ContribOpenStaxPreCalc

Ufafanuzi: SEKONDARI

Jinsi ya: Kutokana na seti ya namba, onyesha ikiwa zinawakilisha mlolongo wa kijiometri.

Mfano\(\PageIndex{1}\): Finding Common Ratios

Zoezi\(\PageIndex{1A}\)

Zoezi\(\PageIndex{1B}\)

Jinsi ya: Kutokana na muda wa kwanza na jambo la kawaida, pata masharti manne ya kwanza ya mlolongo wa kijiometri.

Mfano\(\PageIndex{2}\): Writing the Terms of a Geometric Sequence

Zoezi\(\PageIndex{2}\)

Kumbuka: formula ya kujirudia kwa mlolongo wa kijiometri

Jinsi ya: Kutokana na masharti kadhaa ya kwanza ya mlolongo wa kijiometri, andika formula yake ya kujirudia.

Mfano\(\PageIndex{3}\): Using Recursive Formulas for Geometric Sequences

Zoezi\(\PageIndex{3}\)

Kumbuka: FORMULA YA WAZI KWA MLOLONGO WA KIJI

Mfano\(\PageIndex{4}\): Writing Terms of Geometric Sequences Using the Explicit Formula

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\): Writing an Explicit Formula for the nth Term of a Geometric Sequence

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\): Solving Application Problems with Geometric Sequences

Zoezi\(\PageIndex{6}\)

Wachangiaji na Majina

formula ya kujirudia kwa muda wa nth wa mlolongo wa kijiometri	\(a_n=ra_{n−1}\),\(n≥2\)
formula wazi kwa muda wa nth wa mlolongo wa kijiometri	\(a_n=a_1r^{n−1}\)