8.4: Kuratibu Polar - Grafu

Last updated
Save as PDF

Page ID: 181038

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mtihani equations polar kwa ulinganifu.
Grafu milinganyo ya polar kwa pointi za kupanga.

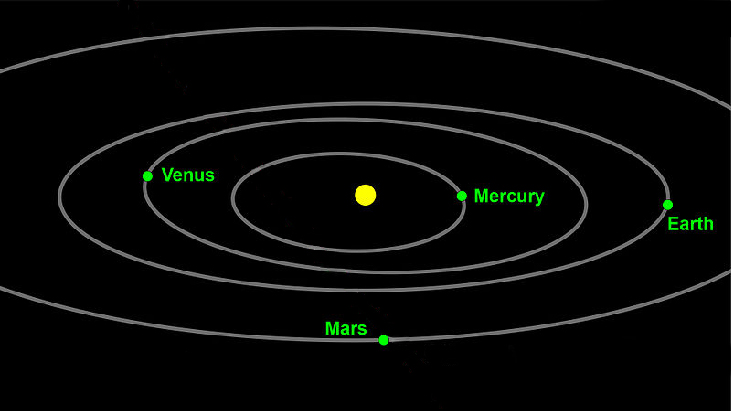
Sheria ya Kwanza ya Keplar ya Sayari Motion anasema kuwa sayari hoja kupitia nafasi katika elliptical, orbits mara kwa mara kuhusu jua, kama inavyoonekana katika Kielelezo$\PageIndex{1}$. Wao ni katika mwendo wa mara kwa mara, hivyo kurekebisha nafasi halisi ya sayari yoyote ni halali kwa muda tu. Kwa maneno mengine, tunaweza kurekebisha nafasi ya sayari ya papo hapo tu. Hii ni moja ya maombi ya kuratibu polar, kuwakilishwa kama$(r,\theta)$. Sisi kutafsiri$r$ kama umbali kutoka jua na$\theta$ kama kuzaa angular sayari, au mwelekeo wake kutoka hatua fasta juu ya jua. Katika sehemu hii, tutazingatia mfumo wa polar na grafu zinazozalishwa moja kwa moja kutoka kwa kuratibu za polar.

Mfano wa mfumo wa jua na jua katikati na njia za sayari Mercury, Venus, Dunia, na Mars umeonyeshwa. — Kielelezo$\PageIndex{1}$: Sayari kufuata njia elliptical kama wao obiti kuzunguka Sun. (mikopo: mabadiliko ya kazi na NASA/JPL-Caltech)

Kupima Ulinganifu wa Polar kwa ulinganifu

Kama vile equation mstatili kama vile$y=x^2$ inaelezea uhusiano kati$x$ na$y$ kwenye gridi ya Cartesian, equation polar inaelezea uhusiano kati$r$ na$\theta$ kwenye gridi ya polar. Kumbuka kwamba kuratibu jozi$(r,\theta)$ inaonyesha kwamba sisi hoja kinyume chake kutoka mhimili polar (chanya$x$ -axis) kwa angle ya$\theta$, na kupanua ray kutoka pole (asili)$r$ vitengo katika mwelekeo wa$\theta$. Vipengele vyote vinavyolingana na equation ya polar ni kwenye grafu.

Ulinganifu ni mali ambayo inatusaidia kutambua na kupanga njama ya equation yoyote. Kama equation ina grafu ambayo ni symmetric kuhusiana na mhimili, inamaanisha kwamba kama sisi folded grafu katika nusu juu ya mhimili kwamba, sehemu ya grafu upande mmoja ingekuwa sambamba na sehemu upande wa pili. Kwa kufanya vipimo vitatu, tutaona jinsi ya kutumia mali ya ulinganifu kwa usawa wa polar. Zaidi ya hayo, tutatumia ulinganifu (pamoja na kupanga njama muhimu, zero, na maximums ya$r$) kuamua grafu ya equation polar.

Katika mtihani wa kwanza, tunazingatia ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$ ($y$-axis). Sisi kuchukua nafasi$(r,\theta)$ na$(−r,−\theta)$ kuamua kama equation mpya ni sawa na equation awali. Kwa mfano, tuseme tunapewa equation$r=2 \sin \theta$;

\[\begin{align*} r&= 2 \sin \theta \\ -r&= 2 \sin -\theta \qquad \text{Replace } (r,\theta) \text{ with }(-r,-\theta). \\ -r&= -2 \sin \theta \qquad \text{Identity: }\sin(-\theta)=-\sin \theta. \\ r&= 2 \sin \theta \qquad \text{Multiply both sides by }-1 \end{align*}\]

Equation hii inaonyesha ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$.

Katika mtihani wa pili, tunazingatia ulinganifu kwa heshima na mhimili wa polar ($x$-axis). Sisi kuchukua nafasi$(r,\theta)$ na$(r,−\theta)$ au$(−r,\pi−\theta)$ kuamua usawa kati ya equation majaribio na awali. Kwa mfano, tuseme tunapewa equation$r=1−2 \cos \theta$.

\[\begin{align*} r&= 1-2 \cos \theta \\ r&= 1-2 \cos(-\theta)\qquad \text{Replace }(r,\theta) \text{ with }(r,-\theta). \\ r&= 1-2 \cos \theta \qquad \text{Even/Odd identity} \end{align*}\]

Grafu ya equation hii inaonyesha ulinganifu kwa heshima na mhimili wa polar.

Katika mtihani wa tatu, tunazingatia ulinganifu kwa heshima na pole (asili). Sisi kuchukua nafasi$(r,\theta)$ na$(−r,\theta)$ kuamua kama equation majaribio ni sawa na equation awali. Kwa mfano, tuseme tunapewa equation$r=2 \sin(3\theta)$.

$r=2 \sin(3\theta)$

$−r=2 \sin(3\theta)$

Equation imeshindwa mtihani ulinganifu, lakini hiyo haina maana kwamba si ulinganifu kwa heshima na pole. Kupitisha moja au zaidi ya vipimo vya ulinganifu huthibitisha kwamba ulinganifu utaonyeshwa kwenye grafu. Hata hivyo, kushindwa vipimo vya ulinganifu haimaanishi kuwa grafu haitakuwa sawa na mstari$\theta=\dfrac{\pi}{2}$, mhimili wa polar, au pole. Katika matukio haya, tunaweza kuthibitisha kwamba ulinganifu upo kwa kupanga njama kuonyesha pointi katika mhimili dhahiri wa ulinganifu au pole. Upimaji wa ulinganifu ni mbinu ambayo inafungua graphing ya equations polar, lakini matumizi yake si kamilifu.

Kumbuka: vipimo vya ulinganifu

Equation polar inaelezea curve kwenye gridi ya polar. Grafu ya equation ya polar inaweza kupimwa kwa aina tatu za ulinganifu, kama inavyoonekana kwenye Mchoro$\PageIndex{2}$.

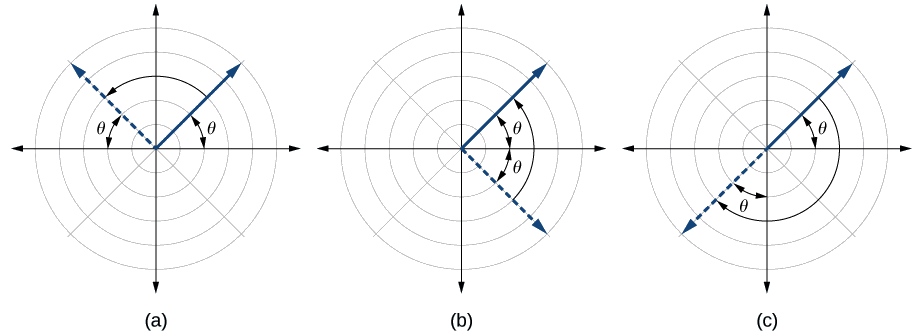
3 grafu upande kwa upande. (A) inaonyesha ray kupanua katika Q 1 na toleo lake linganifu katika Q 2. (B) inaonyesha ray kupanua katika Q 1 na toleo lake linganifu katika Q 4. (C) inaonyesha ray kupanua katika Q 1 na toleo lake linganifu katika Q 3. Angalia maelezo kwa maelezo zaidi. — Kielelezo$\PageIndex{2}$: (a) Grafu ni sawa na heshima na mstari$\theta=\dfrac{\pi}{2}$ (y-axis) ikiwa inabadilisha$(r,\theta)$ na$(−r,−\theta)$ mavuno ya equation sawa. (b) Grafu ni sawa na heshima ya mhimili wa polar (x-axis) ikiwa hubadilisha$(r,\theta)$ na$(r,−\theta)$ au$(−r,\pi−\theta)$ hutoa equation sawa. (c) Grafu ni symmetric kwa heshima na pole (asili) kama kuchukua nafasi$(r,\theta)$ na$(−r,\theta)$ mavuno equation sawa.

Jinsi ya: Kutokana na equation polar, mtihani kwa ulinganifu.

Badilisha mchanganyiko sahihi wa vipengele kwa$(r,\theta)$:$(−r,−\theta)$ kwa$\theta=\dfrac{\pi}{2}$ ulinganifu;$(r,−\theta)$ kwa ulinganifu wa mhimili wa polar; na$(−r,\theta)$ kwa ulinganifu kwa heshima na pole.
Ikiwa equations kusababisha ni sawa katika moja au zaidi ya vipimo, grafu hutoa ulinganifu uliotarajiwa.

Mfano$\PageIndex{1}$: Testing a Polar Equation for Symmetry

Mtihani equation$r=2 \sin \theta$ kwa ulinganifu.

Suluhisho

Mtihani kwa kila aina tatu za ulinganifu.

1) Kubadilisha$(r,\theta)$ na$(−r,−\theta)$ mavuno matokeo sawa. Hivyo, grafu ni symmetric kwa heshima na mstari$\theta=\dfrac{\pi}{2}$.

$−r=2 \sin(−\theta)$

$−r=−2 \sin \theta$Hata-isiyo ya kawaida utambulisho

$r=2 \sin \theta$Kuzidisha kwa$−1$

Imepita

2) Kubadilisha$\theta$ na$−\theta$ haitoi usawa sawa. Kwa hiyo, grafu inashindwa mtihani na inaweza au haipatikani kwa heshima na mhimili wa polar.

$r=2 \sin(−\theta)$

$r=−2 \sin \theta$Hata-isiyo ya kawaida utambulisho

$r=−2 \sin \theta ≠ 2 \sin \theta$

Imeshindwa

3) Kubadilisha$r$ na$–r$ mabadiliko equation na inashindwa mtihani. Grafu inaweza au haipatikani kwa heshima na pole.

$−r=2 \sin \theta$

$r=−2 \sin \theta ≠2 \sin \theta$

Imeshindwa

Uchambuzi

Kutumia calculator graphing, tunaweza kuona kwamba equation$r=2 \sin \theta$ ni mduara unaozingatia saa$(0,1)$ na Radius$r=1$ na ni kweli symmetric kwa mstari$\theta=\dfrac{\pi}{2}$. Tunaweza pia kuona kwamba grafu haipatikani na mhimili wa polar au pole. Angalia Kielelezo$\PageIndex{3}$.

Grafu ya mduara uliopewa kwenye gridi ya kuratibu polar. Center ni saa (0,1), na ina Radius 1. — Kielelezo$\PageIndex{3}$

Zoezi$\PageIndex{1}$

Mtihani equation kwa ulinganifu:$r=−2 \cos \theta$.

Jibu: Equation inashindwa mtihani wa ulinganifu kwa heshima$\theta=\dfrac{\pi}{2}$ na mstari na kwa heshima na pole. Inapita mtihani wa ulinganifu wa mhimili wa polar.

Kuchora Ulinganisho wa Polar na Pointi za kupanga

Kwa grafu katika mfumo wa kuratibu mstatili tunajenga meza ya$x$ na$y$ maadili. Kwa grafu katika mfumo wa kuratibu polar tunajenga meza ya$\theta$ na$r$ maadili. Sisi kuingia maadili ya$\theta$ katika equation polar na mahesabu$r$. Hata hivyo, kutumia mali ya ulinganifu na kutafuta maadili muhimu ya$\theta$ na$r$ ina maana mahesabu machache yatahitajika.

Kupata Zeros na Maxima

Ili kupata zeros ya equation polar, sisi kutatua kwa maadili ya$\theta$ kwamba matokeo katika$r=0$. Kumbuka kwamba, ili kupata zero za kazi nyingi, tunaweka equation sawa na sifuri na kisha kutatua$x$. Tunatumia mchakato huo kwa equations polar. Kuweka$r=0$, na kutatua kwa$\theta$.

Kwa aina nyingi tutakutana, thamani ya juu ya equation ya polar inapatikana kwa kubadili maadili hayo ya$\theta$ ndani ya equation ambayo husababisha thamani ya juu ya kazi trigonometric. Fikiria$r=5 \cos \theta$; umbali wa juu kati ya pembe na pole ni$5$ vitengo. Thamani ya juu ya kazi ya cosine ni$1$ wakati$\theta=0$, hivyo equation yetu ya polar ni$5 \cos \theta$, na thamani$\theta=0$ itazaa kiwango cha juu$| r |$.

Vile vile, thamani ya juu ya kazi ya sine ni$1$ wakati$\theta=\dfrac{\pi}{2}$, na kama equation yetu ya polar ni$r=5 \sin \theta$, thamani$\theta=\dfrac{\pi}{2}$ itazaa kiwango cha juu$| r |$. Tunaweza kupata maelezo ya ziada kwa kuhesabu maadili ya$r$ wakati$\theta=0$. Hizi pointi itakuwa polar mhimili intercepts, ambayo inaweza kuwa na manufaa katika kuchora grafu na kutambua Curve ya equation Polar.

Mfano$\PageIndex{2}$: Finding Zeros and Maximum Values for a Polar Equation

Kutumia equation katika Mfano$\PageIndex{1}$, kupata zero na upeo$| r |$ na, ikiwa ni lazima, mhimili polar intercepts ya$r=2 \sin \theta$.

Suluhisho

Ili kupata zero, weka$r$ sawa na sifuri na usuluhishe$\theta$.

\[\begin{align*} 2 \sin \theta &= 0 \\ \sin \theta &= 0 \\ \theta &= {\sin}^{-1} 0 \\ \theta &= n\pi \qquad \text{where n is an integer} \end{align*}\]

Badilisha yoyote moja ya$\theta$ maadili katika equation. Tutatumia$0$.

\[\begin{align*} r&= 2 \sin(0) \\ r&= 0 \end{align*}\]

Pointi$(0,0)$ na$(0,\pm n\pi)$ ni zero za equation. Wote sanjari, hivyo hatua moja tu inaonekana kwenye grafu. Hatua hii pia ni mhimili wa polar pekee.

Ili kupata thamani ya juu ya equation, angalia thamani ya juu ya kazi ya trigonometric$\sin \theta$, ambayo hutokea wakati wa$\theta=\dfrac{\pi}{2}\pm 2k\pi$ kusababisha$\sin\left(\dfrac{\pi}{2}\right)=1$. Mbadala$\dfrac{\pi}{2}$ kwa ajili ya$\theta$.

\[\begin{align*} r&= 2 \sin\left(\dfrac{\pi}{2}\right) \\ r&= 2(1) \\ r&= 2 \end{align*}\]

Uchambuzi

Hatua$\left(2,\dfrac{\pi}{2}\right)$ itakuwa thamani ya juu kwenye grafu. Hebu tufanye pointi chache zaidi ili kuthibitisha grafu ya mduara. Angalia Jedwali$\PageIndex{1}$ na Kielelezo$\PageIndex{4}$.

Jedwali$\PageIndex{1}$
$\theta$	$r=2 \sin \theta$	$r$
\ (\ theta\) ">$0$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin(0)=0$	\ (r\) ">$0$
\ (\ theta\) ">$\dfrac{\pi}{6}$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{6}\right)=1$	\ (r\) ">$1$
\ (\ theta\) ">$\dfrac{\pi}{3}$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73$	\ (r\) ">$1.73$
\ (\ theta\) ">$\dfrac{pi}{2}$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{2}\right)=2$	\ (r\) ">$2$
\ (\ theta\) ">$\dfrac{2\pi}{3}$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73$	\ (r\) ">$1.73$
\ (\ theta\) ">$\dfrac{5\pi}{6}$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin\left(\dfrac{5\pi}{6}\right)=1$	\ (r\) ">$1$
\ (\ theta\) ">$\pi$	\ (r=2\ dhambi\ theta\) ">$r=2 \sin(\pi)=0$	\ (r\) ">$0$

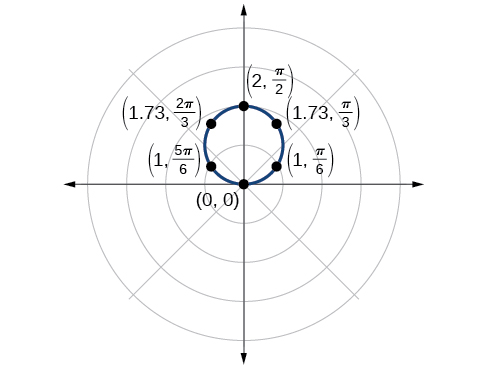
Grafu ya mduara kwenye gridi ya kuratibu polar. kituo cha ni katika (0,1), na ina Radius 1. Pointi sita kwenye mzunguko ni alama: (0,0), (1, pi/6), (1.3, pi/3), (2, pi/2), (1.73, 2pi/3), na (1, 5pi/6). — Kielelezo$\PageIndex{4}$

Zoezi$\PageIndex{2}$

Bila kugeuka kwenye kuratibu za Cartesian, jaribu usawa uliotolewa kwa ulinganifu na upate zero na maadili ya juu ya$| r |$:$r=3 \cos \theta$.

Jibu: Majaribio yatafunua ulinganifu kuhusu mhimili wa polar. Zero ni$\left(0,\dfrac{\pi}{2}\right)$, na thamani ya juu ni$(3,0)$.

Kuchunguza miduara

Sasa tumeona equation ya mduara katika mfumo wa kuratibu polar. Katika mifano miwili iliyopita, equation hiyo ilitumika kuonyesha tabia ya ulinganifu na kuonyesha jinsi ya kupata zero, maadili ya kiwango cha juu, na pointi zilizopangwa zinazozalishwa grafu. Hata hivyo, mduara ni moja tu ya maumbo mengi katika seti ya curves polar.

Kuna tano classic polar curves: cardioids, limaons, lemniscates, rose curves, na spirals Archimedes '. Tutagusa kwa ufupi juu ya fomu za polar kwa mduara kabla ya kuhamia kwenye curves za classic na tofauti zao.

FORMULA KWA EQUATION YA MDUARA

Baadhi ya formula zinazozalisha grafu ya mduara katika kuratibu za polar hutolewa$r=a \cos \theta$ na$r=a \sin \theta$, ambapo ni kipenyo cha mduara au umbali kutoka kwa pole hadi hatua ya mbali zaidi kwenye mzunguko. Radi ni$\dfrac{|a|}{2}$, au nusu ya kipenyo. Kwa$r=a \cos \theta$, kituo cha ni$\left(\dfrac{a}{2},0\right)$. Kwa$r=a \sin \theta$, kituo cha ni$\left(\dfrac{a}{2},\pi\right)$. Kielelezo$\PageIndex{5}$ kinaonyesha grafu ya duru hizi nne.

Grafu nne kwa upande. Wote wana Radius thamani kamili ya/2. Kwanza ni r=acos (theta), a — Kielelezo$\PageIndex{5}$

Mfano$\PageIndex{3}$: Sketching the Graph of a Polar Equation for a Circle

Mchoro grafu ya$r=4 \cos \theta$.

Suluhisho

Kwanza, kupima equation kwa ulinganifu, tunaona kwamba grafu ni symmetric kuhusu mhimili polar. Kisha, tunapata zero na$| r |$ upeo wa$r=4 \cos \theta$. Kwanza, kuweka$r=0$, na kutatua kwa$\theta$. Hivyo, sifuri hutokea$\theta=\dfrac{\pi}{2}\pm k\pi$. Hatua muhimu ya njama ni$\left(0,\dfrac{\pi}{2}\right)$.

Ili kupata thamani ya juu ya$r$, kumbuka kuwa thamani ya juu ya kazi ya cosine ni$1$ wakati$\theta=0\pm 2k\pi$. Mbadala$\theta=0$ katika equation:

\[\begin{align*} r&= 4 \cos \theta\\ r&= 4 \cos(0)\\ r&= 4(1)\\ &= 4 \end{align*}\]

Thamani ya juu ya equation ni$4$. Hatua muhimu ya njama ni$(4, 0)$.

Kama$r=4 \cos \theta$ ilivyo sawa na heshima ya mhimili wa polar, tunahitaji tu kuhesabu$r$ -maadili kwa$θ$ zaidi ya muda$[0, \pi]$. Pointi katika quadrant ya juu inaweza kuonekana kwa quadrant ya chini. Fanya meza ya maadili sawa na Jedwali$\PageIndex{2}$. Grafu inavyoonyeshwa kwenye Kielelezo$\PageIndex{6}$.

Jedwali$\PageIndex{2}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	$4$	$3.46$	$2.83$	$2$	$0$	$−2$	$−2.83$	$−3.46$	$4$

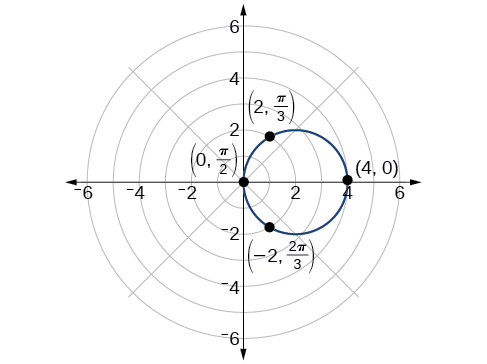
Grafu ya 4=4cos (theta) katika kuratibu polar. Pointi (0, pi/2), (-2, 2pi/3), (4,0), na (2, pi/3) ni alama kwenye mzunguko. — Kielelezo$\PageIndex{6}$

Kuchunguza Cardioids

Wakati kutafsiri kutoka kuratibu polar kwa kuratibu Cartesian inaweza kuonekana rahisi katika baadhi ya matukio, graphing curves classic ni kweli chini ngumu katika mfumo polar. Curve inayofuata inaitwa cardioid, kama inafanana na moyo. Sura hii mara nyingi hujumuishwa na familia ya curves inayoitwa limaçons, lakini hapa tutajadili cardioid peke yake.

FORMULA KWA CARDIOID

Njia zinazozalisha grafu za cardioid hutolewa$r=a\pm b \cos \theta$ na$r=a\pm b \sin \theta$ wapi$a>0$,$b>0$, na$\dfrac{a}{b}=1$. Grafu ya cardioid inapita kupitia pole, kama tunavyoweza kuona kwenye Mchoro$\PageIndex{7}$.

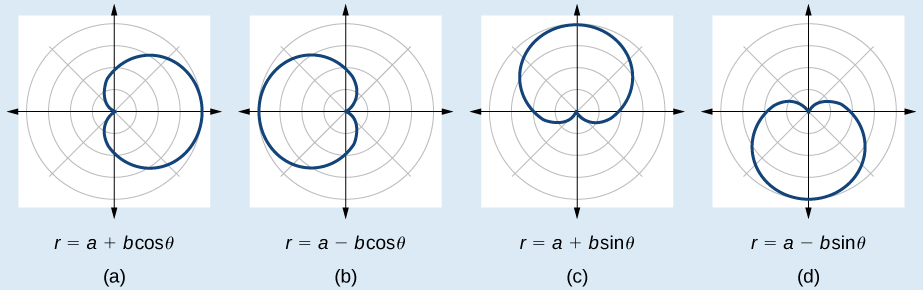
Grafu ya cardioids nne. (A) ni r = a + masanduku (theta). Cardioid kupanua kwa haki. (B) ni r=a-bcos (theta). Cardioid inapanua upande wa kushoto. (C) ni r=a+bsin (theta). Cardioid kupanua juu. (D) ni r=a-bsin (theta). Cardioid inapanua chini. — Kielelezo$\PageIndex{7}$

Jinsi ya: Kutokana na equation ya polar ya cardioid, mchoro grafu yake

Angalia equation kwa aina tatu za ulinganifu.
Pata zero. Weka$r=0$.
Pata thamani ya juu ya equation kulingana na thamani ya juu ya kujieleza trigonometric.
Fanya meza ya maadili kwa$r$ na$\theta$.
Panda pointi na mchoro grafu.

Mfano$\PageIndex{4}$: Sketching the Graph of a Cardioid

Mchoro grafu ya$r=2+2 \cos \theta$.

Suluhisho

Kwanza, kupima equation kwa ulinganifu, tunaona kwamba grafu ya equation hii itakuwa symmetric kuhusu mhimili polar. Kisha, tunapata zero na maximums. Kuweka$r=0$, tuna$\theta=\pi+2k\pi$. Zero ya equation iko katika$(0,\pi)$. Grafu hupita kupitia hatua hii.

Thamani ya juu ya$r=2+2 \cos \theta$ hutokea wakati$\cos \theta$ ni kiwango cha juu, ambayo ni wakati$\cos \theta=1$ au wakati$\theta=0$. Mbadala$\theta=0$ katika equation, na kutatua kwa$r$.

\[\begin{align*} r&= 2+2 \cos(0)\\ r&= 2+2(1)\\ &= 4 \end{align*}\]

Hatua$(4,0)$ ni thamani ya juu kwenye grafu.

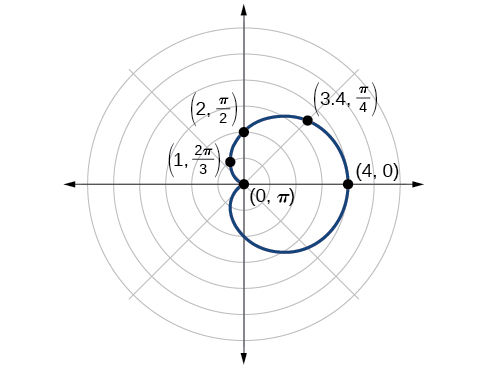
Tuligundua kwamba equation ya polar ni sawa na heshima ya mhimili wa polar, lakini ikiwa inaenea kwa quadrants zote nne, tunahitaji kupanga maadili juu ya muda$[0, \pi]$. Sehemu ya juu ya grafu inaonekana juu ya mhimili wa polar. Kisha, tunafanya meza ya maadili, kama katika Jedwali$\PageIndex{3}$, na kisha tunapanga njama na kuteka grafu. Angalia Kielelezo$\PageIndex{8}$.

Jedwali$\PageIndex{3}$
	0	$\dfrac{π}{4}$	$\dfrac{π}{2}$	$\dfrac{2π}{3}$	$π$
r	4	3.41	2	1	0

Grafu ya r=2+2cos (theta). Cardioid kupanua kwa haki. Pointi makali (0, pi), (4,0), (3.4, pi/4), (2, pi/2), na (1, 2pi/3) huonyeshwa. — Kielelezo$\PageIndex{8}$

Kuchunguza Limaçons

Neno limaçon ni Kifaransa cha Kale kwa ajili ya “konokono,” jina linaloelezea umbo la grafu. Kama ilivyoelezwa hapo awali, cardioid ni mwanachama wa familia ya limaçon, na tunaweza kuona kufanana katika grafu. Picha nyingine katika jamii hii ni pamoja na limaçon moja-kitanzi na mbili kitanzi (au ndani-kitanzi) limaçon. Wakati mwingine limaçons kitanzi hujulikana kama limaçons dimpled wakati$1<\dfrac{a}{b}<2$ na convex limaçons wakati$\dfrac{a}{b}≥2$.

FORMULA KWA LIMAÇONS MOJA YA KITANZI

Fomu zinazozalisha grafu ya limaçon moja ya kitanzi kilichopunguzwa hutolewa$r=a\pm b \cos \theta$ na$r=a\pm b \sin \theta$ wapi$a>0$$b>0$, na$1<ab<2$. Grafu zote nne zinaonyeshwa kwenye Kielelezo$\PageIndex{9}$.

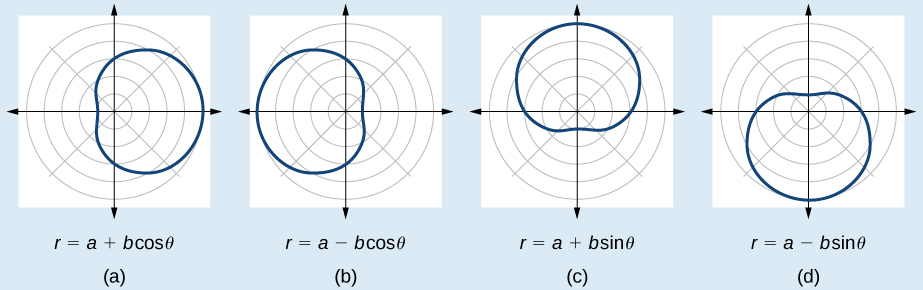
Nne limaçons dimpled upande kwa upande. (A) ni r=a+bcos (theta). Kupanua kwa haki. (B) ni r=a-bcos (theta). Kupanua upande wa kushoto. (C) ni r=a+bsin (theta). Kupanua hadi. (D) ni r=a-bsin (theta). Kupanua chini. — Kielelezo$\PageIndex{9}$

Jinsi ya: Kutokana na equation ya polar kwa limaçon moja ya kitanzi, mchoro grafu

Mtihani equation kwa ulinganifu. Kumbuka kwamba kushindwa mtihani wa ulinganifu haimaanishi kwamba sura haitaonyesha ulinganifu. Mara nyingi ulinganifu unaweza kujidhihirisha wakati pointi zimepangwa.
Pata zero.
Pata maadili ya juu kulingana na kujieleza kwa trigonometric.
Fanya meza.
Panda pointi na mchoro grafu.

Mfano$\PageIndex{5}$: Sketching the Graph of a One-Loop Limaçon

Grafu equation$r=4−3 \sin \theta$.

Suluhisho

Kwanza, kupima equation kwa ulinganifu, tunaona kwamba inashindwa vipimo vyote vitatu vya ulinganifu, maana yake ni kwamba grafu inaweza au isionyeshe ulinganifu, hivyo hatuwezi kutumia ulinganifu kutusaidia kutuunga graph. Hata hivyo, equation hii ina grafu inayoonyesha wazi ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$, lakini inashindwa vipimo vyote vitatu vya ulinganifu. Calculator ya graphing itaonyesha mara moja ubora wa kutafakari wa grafu.

Kisha, tunapata zero na upeo, na njama pointi za kutafakari ili kuthibitisha ulinganifu wowote. Kuweka$r=0$ matokeo kwa$\theta$ kuwa haijulikani. Hii ina maana gani? Jinsi gani inaweza$\theta$ kuwa undefined? Angle$\theta$ haijulikani kwa thamani yoyote ya$\sin \theta>1$. Kwa hiyo,$\theta$ ni undefined kwa sababu hakuna thamani ya$\theta$ ambayo$\sin \theta>1$. Kwa hiyo, grafu haipiti kupitia pole. Labda grafu inavuka mhimili wa polar, lakini sio kwenye pole. Tunaweza kuchunguza intercepts nyingine kwa kuhesabu$r$ wakati$\theta=0$.

\[\begin{align*} r(0)&= 4-3 \sin(0)\\ r&= 4-3\cdot 0\\ &= 4 \end{align*}\]

Kwa hiyo, kuna angalau moja ya mhimili wa polar inakataza saa$(4,0)$.

Next, kama thamani ya juu ya kazi sine ni$1$ wakati$\theta=\dfrac{\pi}{2}$, sisi badala$\theta=\dfrac{\pi}{2}$ katika equation na kutatua kwa$r$. Hivyo,$r=1$.

Fanya meza ya kuratibu sawa na Jedwali$\PageIndex{4}$.

Jedwali$\PageIndex{4}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$4$	$2.5$	$1.4$	$1$	$1.4$	$2.5$	$4$	$5.5$	$6.6$	$7$	$6.6$	$5.5$	$4$

Grafu inavyoonyeshwa kwenye Kielelezo$\PageIndex{10}$.

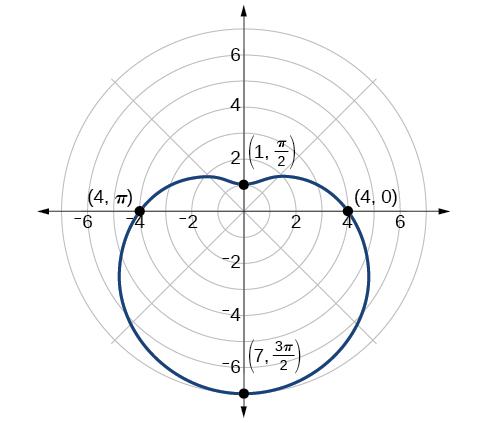
Grafu ya limaçon r=4-3sin (theta). Kupanua chini. Pointi makali huonyeshwa: (1, pi/2), (4,0), (4, pi), na (7, 3pi/2). — Kielelezo$\PageIndex{10}$: Limaçon moja ya kitanzi

Uchambuzi

Huu ni mfano wa safu ambayo kufanya meza ya maadili ni muhimu kuzalisha grafu sahihi. Vipimo vya ulinganifu vinashindwa; sifuri haijulikani. Ingawa inaweza kuwa dhahiri kwamba equation kuwashirikisha$\sin \theta$ ni uwezekano symmetric kuhusiana na mstari$\theta=\dfrac{\pi}{2}$, kutathmini pointi zaidi husaidia kuthibitisha kwamba grafu ni sahihi.

Zoezi$\PageIndex{3}$

Mchoro grafu ya$r=3−2 \cos \theta$.

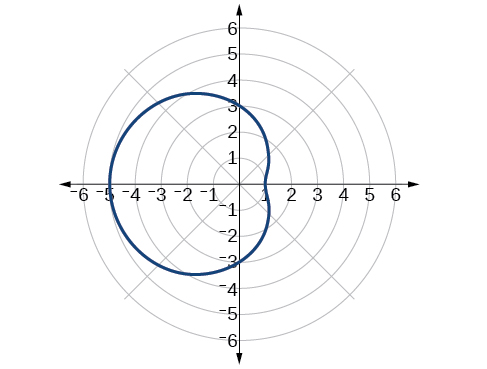
Jibu: $Grafu ya limaçon r=3-2cos (theta). Kupanua upande wa kushoto.$
Kielelezo$\PageIndex{11}$

Aina nyingine ya limaçon, limaçon ya ndani ya kitanzi, inaitwa kwa kitanzi kilichoundwa ndani ya sura ya jumla ya limaçon. Iligunduliwa na msanii wa Ujerumani Albrecht Dürer (1471-1528), ambaye alifunua njia ya kuchora limaçon ya ndani ya kitanzi katika kitabu chake cha 1525 Underweysung der Messing. Karne moja baadaye, baba wa mwanahisabati Blaise Pascal, Étienne Pascal (1588-1651), aligundua tena.

FORMULA KWA LIMAÇONS YA NDANI YA KITANZI

Njia zinazozalisha limaçons ya ndani ya kitanzi hutolewa$r=a\pm b\cos \theta$ na$r=a\pm b \sin \theta$ wapi$a>0$,$b>0$, na$a<b$. Grafu ya limaçon ya ndani ya kitanzi hupita kupitia pole mara mbili: mara moja kwa kitanzi cha nje, na mara moja kwa kitanzi cha ndani. Angalia Mchoro 10.5.12 kwa grafu.

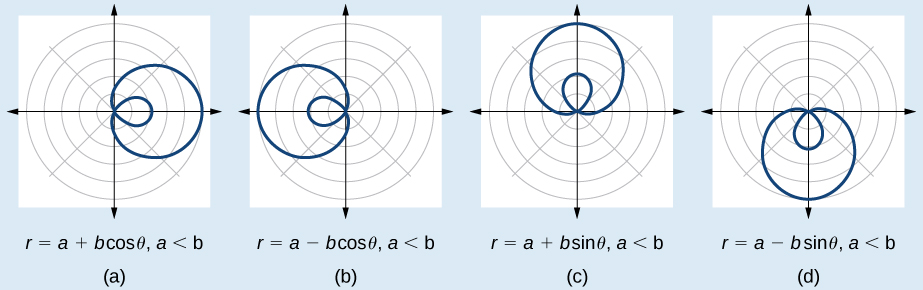
Grafu ya nne ndani kitanzi limaçons upande kwa upande. (A) ni r=a+bcos (theta), <b. kupanuliwa kwa haki. (B) ni-bcos (theta), a<b. inaenea upande wa kushoto. (C) ni r=a+bsin (theta), <b. inaenea juu. (D) ni r=a-bsin (theta), <b. inaenea chini. — Kielelezo$\PageIndex{12}$

Mfano$\PageIndex{6}$: Sketching the Graph of an Inner-Loop Limaçon

Mchoro grafu ya$r=2+5 \cos \theta$.

Suluhisho

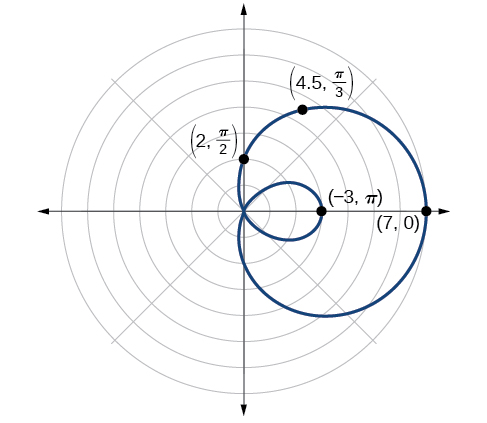
Kupima kwa ulinganifu, tunaona kwamba grafu ya equation ni sawa na mhimili wa polar. Kisha, kutafuta zero inaonyesha kwamba wakati$r=0$,$\theta=1.98$. Upeo$| r |$ unapatikana wakati$\cos \theta=1$ au wakati$\theta=0$. Hivyo, kiwango cha juu kinapatikana kwa hatua$(7, 0)$.

Ingawa tumepata ulinganifu, sifuri, na kiwango cha juu, kupanga njama zaidi itasaidia kufafanua sura, na kisha muundo utaibuka. Angalia Jedwali$\PageIndex{5}$.

Jedwali$\PageIndex{5}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$7$	$6.3$	$4.5$	$2$	$−0.5$	$−2.3$	$−3$	$−2.3$	$−0.5$	$2$	$4.5$	$6.3$	$7$

Kama inavyotarajiwa, maadili huanza kurudia baada$\theta=\pi$. Grafu inavyoonyeshwa kwenye Kielelezo$\PageIndex{13}$.

Grafu ya ndani kitanzi limaçon r=2+5cos (theta). Inaenea kwa haki. Pointi kwenye makali yaliyopangwa ni (7,0), (4.5, pi/3), (2, pi/2), na (-3, pi). — Kielelezo$\PageIndex{13}$: Ndani-kitanzi limaçon

Kuchunguza Lemniscates

Lemniscate ni pembe ya polar inayofanana na ishara ya infinity$\infty$ au takwimu$8$. Kuzingatia kwenye pole, lemniscate ni sawa na ufafanuzi.

FORMULA KWA AJILI YA LEMNISCATES

Fomu zinazozalisha grafu ya lemniscate hutolewa$r^2=a^2 \cos 2\theta$ na$r^2=a^2 \sin 2\theta$ wapi$a≠0$. Fomu$r^2=a^2 \sin 2\theta$ hiyo ni sawa na heshima na pole. Fomu$r^2=a^2 \cos 2\theta$ hiyo ni sawa na heshima na pole, mstari$\theta=\dfrac{\pi}{2}$, na mhimili wa polar. Angalia Kielelezo$\PageIndex{14}$ kwa grafu.

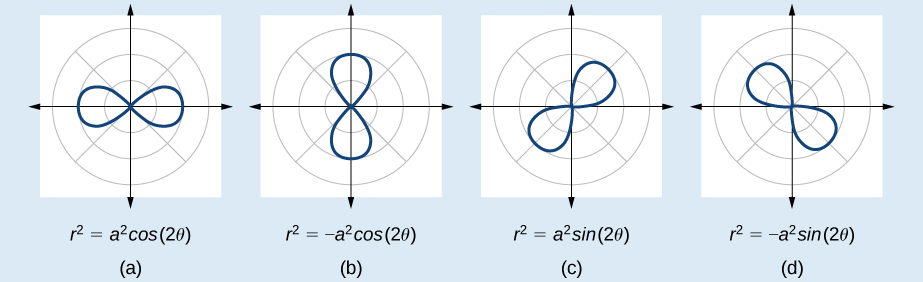
Grafu nne za lemniscates upande kwa upande. A ni r ^ 2 = a ^ 2 * cos (2theta). Takwimu ya usawa nane, kwenye x-axis. (B) ni r ^ 2 = - a ^ 2* cos (2theta). Takwimu ya wima nane, juu ya mhimili y. (C) ni r ^ 2 = a ^ 2* dhambi (2theta). Diagonal takwimu nane kwenye mstari y = x. (D) ni r ^ 2 = -a ^ 2 *dhambi (2theta). Takwimu ya diagonal nane kwenye mstari y=-x. — Kielelezo$\PageIndex{14}$

Mfano$\PageIndex{7}$: Sketching the Graph of a Lemniscate

Mchoro grafu ya$r^2=4 \cos 2\theta$.

Suluhisho

Equation inaonyesha ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$, mhimili wa polar, na pole.

Hebu tupate zero. Inapaswa kuwa mara kwa mara kwa sasa, lakini tutakaribia equation hii tofauti kidogo kwa kufanya badala$u=2\theta$.

\[\begin{align*} 0 &= 4 \cos 2\theta \\ 0 &= 4 \cos u \\ 0 &= \cos u \\ {\cos}^{-1} 0 &= \dfrac{\pi}{2} \\ u &= \dfrac{\pi}{2} \qquad \text{Substitute } 2\theta \text{ back in for } u. \\ 2\theta &= \dfrac{\pi}{2} \\ \theta &= \dfrac{\pi}{4} \end{align*}\]

Hivyo, uhakika$\left(0,\dfrac{\pi}{4}\right)$ ni sifuri ya equation.

Sasa hebu tupate thamani ya juu. Tangu upeo wa$\cos u=1$ wakati$u=0$, kiwango cha juu$\cos 2\theta=1$ wakati$2\theta=0$. Hivyo,

\[\begin{align*} r^2 &= 4 \cos(0) \\ r^2 &= 4(1)\\ r^2&= 4 \\ r&= \pm 4\\ &=2 \end{align*}\]

Tuna kiwango cha juu katika$(2, 0)$. Kwa kuwa grafu hii ni sawa na heshima kwa pole, mstari$\theta=\dfrac{\pi}{2}$, na mhimili wa polar, tunahitaji tu kupanga njama katika quadrant ya kwanza.

Fanya meza sawa na Jedwali$\PageIndex{6}$.

Jedwali$\PageIndex{6}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$
$r$	$2$	$\sqrt{2}$	$0$	$\sqrt{2}$	$0$

Panda pointi kwenye grafu, kama ile iliyoonyeshwa kwenye Kielelezo$\PageIndex{15}$.

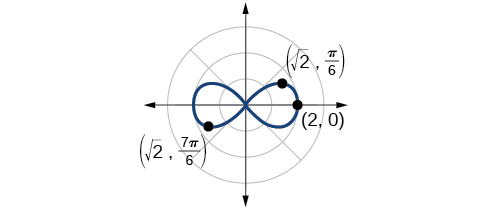
Grafu ya r ^ 2 = 4cos (2theta). Lemniscate ya usawa, pamoja na x-axis. Pointi juu ya makali yaliyopangwa ni (2,0), (rad2, pi/6), (rad2 7pi/6). — Kielelezo$\PageIndex{15}$: Lemniscate

Uchambuzi

Kufanya mbadala kama vile$u=2\theta$ ni mazoezi ya kawaida katika hisabati kwa sababu inaweza kufanya mahesabu rahisi. Hata hivyo, hatupaswi kusahau kuchukua nafasi ya neno la kubadilisha na muda wa awali mwishoni, na kisha tatua kwa haijulikani.

Baadhi ya pointi kwenye graph hii inaweza kuonekana kwa kutumia Trace kazi kwenye TI-84 graphing calculator, na meza Calculator inaweza kuonyesha makosa kwa pointi hizi sawa ya$r$. Hii ni kwa sababu hakuna mizizi halisi ya mraba kwa maadili haya ya$θ$. Kwa maneno mengine, sambamba$r$ -maadili ya$\sqrt{4 \cos(2\theta)}$ ni namba tata kwa sababu kuna idadi hasi chini ya radical.

Kuchunguza Rose Curves

Aina inayofuata ya equation ya polar inazalisha sura ya petal inayoitwa curve ya rose. Ingawa grafu zinaonekana ngumu, equation rahisi ya polar inazalisha muundo.

ROSE CURVES

Fomu zinazozalisha grafu ya curve ya rose hutolewa$r=a \cos n\theta$ na$r=a \sin n\theta$ wapi$a≠0$. Ikiwa$n$ ni hata, curve ina$2n$ petals. Kama$n$ ni isiyo ya kawaida, Curve ina$n$ petals. Angalia Kielelezo$\PageIndex{16}$.

Grafu ya curves mbili rose upande kwa upande. (A) ni r=acos (ntheta), ambapo n ni hata. Petals nane kupanua kutoka asili, sawa spaced. (B) ni r=asin (ntheta) ambapo n ni isiyo ya kawaida. Petals tatu kupanua kutoka asili, sawa spaced. — Kielelezo$\PageIndex{16}$

Mfano$\PageIndex{8}$: Sketching the Graph of a Rose Curve ($n$ Even)

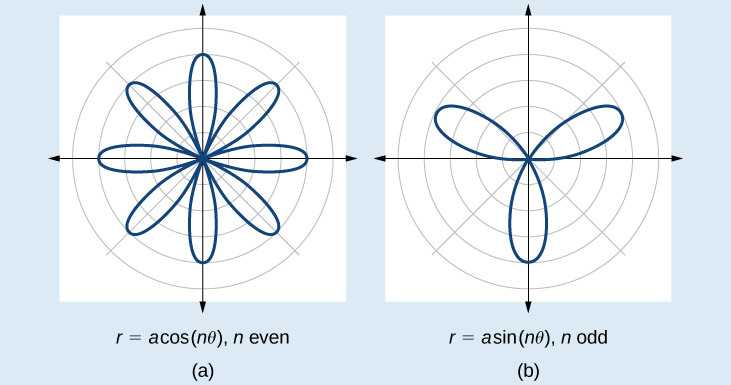
Mchoro grafu ya$r=2 \cos 4\theta$.

Suluhisho

Kupima kwa ulinganifu, tunaona tena kwamba vipimo vya ulinganifu haviambii hadithi nzima. Grafu sio tu ya usawa kwa heshima na mhimili wa polar, lakini pia kwa heshima na mstari$\theta=\dfrac{\pi}{2}$ na pole.

Sasa tutapata zero. Kwanza fanya badala$u=4\theta$.

\[\begin{align*} 0 &= 2 \cos 4\theta \\ 0 &= \cos 4\theta \\ 0 &= \cos u \\ {\cos}^{-1} 0 &=u \\ u &= \dfrac{\pi}{2} \\ 4\theta &= \dfrac{\pi}{2} \\ \theta &=\dfrac{\pi}{8} \end{align*}\]

Zero ni$\theta=\dfrac{\pi}{8}$. uhakika$\left(0,\dfrac{\pi}{8}\right)$ ni juu ya Curve.

Kisha, tunapata kiwango cha juu$| r |$. Tunajua kwamba thamani ya juu ya$\cos u=1$ wakati$\theta=0$. Hivyo,

\[\begin{align*} r &=2 \cos(4\cdot 0) \\ r &=2 \cos(0) \\ r &=2(1)\\ &= 2 \end{align*}\]

uhakika$(2,0)$ ni juu ya Curve.

Grafu ya safu ya rose ina mali ya kipekee, ambayo imefunuliwa katika Jedwali$\PageIndex{7}$.

Jedwali$\PageIndex{7}$
$\theta$	$0$	$\dfrac{\pi}{8}$	$\dfrac{\pi}{4}$	$\dfrac{3\pi}{8}$	$\dfrac{\pi}{2}$	$5π8$	$3π4$
$r$	$2$	$0$	$−2$	$0$	$2$	$0$	$−2$

Kama$r=0$ wakati$\theta=\dfrac{\pi}{8}$, ni busara kugawanya maadili katika meza na$\dfrac{\pi}{8}$ vitengo. Mfano wa uhakika unajitokeza. Angalia aina mbalimbali$r$ za maadili:$2, 0, −2, 0$ na kadhalika. Hii inawakilisha maendeleo ya pembe moja petal kwa wakati mmoja. Kuanzia saa$r=0$, kila petal hadi nje umbali wa$r=2$, na kisha anarudi nyuma$2n$ mara sifuri kwa jumla ya petals nane. Angalia grafu katika Kielelezo$\PageIndex{17}$.

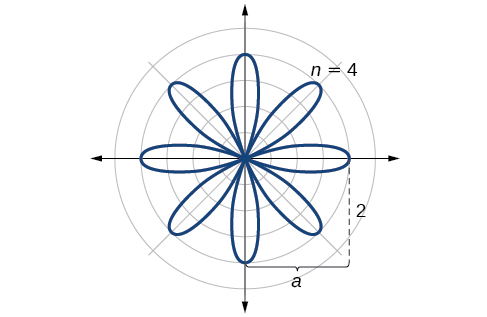
Mchoro wa rose Curve r=2*cos (4 theta). Huenda nje umbali wa 2 kwa kila petal mara 2n (hapa 2*4=mara 8). — Kielelezo$\PageIndex{17}$: Rose Curve,$n$ hata

Uchambuzi

Wakati curves hizi zinapatikana, ni bora kupanga njama kwa utaratibu, kama katika Jedwali$\PageIndex{7}$. Hii inaruhusu sisi kuona jinsi grafu inapiga kiwango cha juu (ncha ya petal), loops nyuma kuvuka pole, hits upeo kinyume, na loops nyuma pole. Hatua hiyo inaendelea mpaka petals zote zinatolewa.

Zoezi$\PageIndex{4}$

Mchoro grafu ya$r=4 \sin(2\theta)$.

Jibu: Grafu ni safu ya rose,$n$ hata

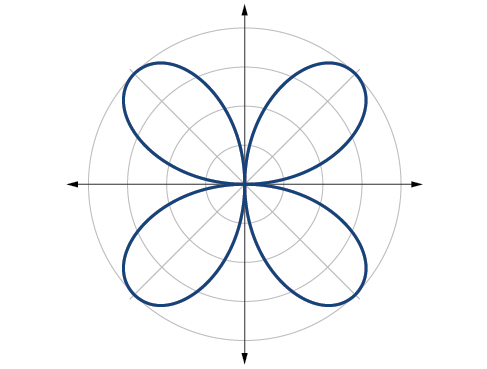
$Grafu ya rose Curve r=4 dhambi (2 theta). Hata - petals nne sawa spaced, kila urefu 4.$
Kielelezo$\PageIndex{18}$

Mfano$\PageIndex{9}$: Sketching the Graph of a Rose Curve ($n$ Odd)

Mchoro grafu ya$r=2 \sin(5\theta)$.

Suluhisho

Grafu ya equation inaonyesha ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$. Kisha, pata zero na upeo. Tutataka kufanya badala$u=5\theta$.

\[\begin{align*} 0 &=2 \sin(5\theta) \\ 0 &=\sin u \\ {\sin}^{-1} 0 &=0 \\ u &=0 \\ 5\theta &=0 \\ \theta &=0 \end{align*}\]

Thamani ya juu imehesabiwa kwa pembe ambapo$\sin \theta$ ni kiwango cha juu. Kwa hiyo,

\[\begin{align*} r&= 2 \sin\left(5\cdot \dfrac{\pi}{2}\right) \\ r&= 2(1)\\ &= 2 \end{align*}\]

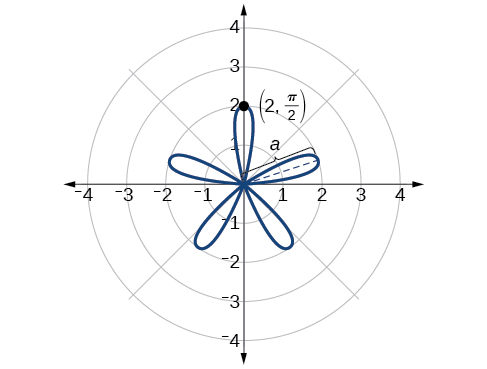
Hivyo, thamani ya juu ya equation polar ni$2$. Hii ni urefu wa kila petal. Kama Curve kwa mazao$n$ isiyo ya kawaida idadi sawa ya petals kama$n$, kutakuwa na petals tano kwenye grafu. Angalia Kielelezo$\PageIndex{19}$.

Unda meza ya maadili sawa na Jedwali$\PageIndex{8}$.

Jedwali$\PageIndex{8}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	\ (0\ 0	$1$	$−1.73$	$2$	$−1.73$	$1$	$0$

Grafu ya rose Curve r = 2sin (5theta). Petals tano sawa spaced karibu asili. Point (2, pi/2) makali ni alama. — Kielelezo$\PageIndex{19}$: Rose Curve,$n$ isiyo ya kawaida

Zoezi$\PageIndex{5}$

Mchoro grafu ya$r=3 \cos(3\theta)$.

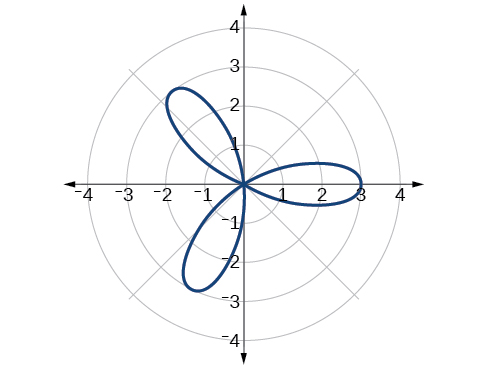
Jibu: $Grafu ya rose Curve r=3cos (3theta). Petals tatu sawa spaced kutoka asili.$
Kielelezo$\PageIndex{20}$

Rose Curve,$n$ isiyo ya kawaida

Kuchunguza Spiral Archimedes '

Equation ya mwisho ya polar tutazungumzia ni ond ya Archimedes, jina lake kwa mvumbuzi wake, mtaalamu wa hisabati wa Kigiriki Archimedes (c 287 BCE - c 212 BC), ambaye anahesabiwa na uvumbuzi mbalimbali katika nyanja za jiometri na mechanics.

OND ARCHIMEDES '

Fomu inayozalisha grafu ya ond ya Archimedes inatolewa na$r=\theta$ kwa$\theta≥0$. Kama$\theta$ ongezeko,$r$ huongezeka kwa kiwango cha mara kwa mara katika njia inayozidi kuongezeka, isiyo na mwisho, inayozunguka. Angalia Kielelezo$\PageIndex{21}$.

Jinsi ya: Kutokana na ond Archimedes 'juu$[ 0,2\pi ]$,sketch the graph

Fanya meza ya maadili$r$ na$\theta$ juu ya kikoa kilichopewa.
Panda pointi na mchoro grafu.

Mfano$\PageIndex{10}$: Sketching the Graph of an Archimedes’ Spiral

Mchoro grafu ya$r=\theta$ juu$[0,2\pi]$.

Suluhisho

Kama$r$ ilivyo sawa$\theta$, njama ya ond ya Archimedes huanza kwenye pole wakati huo$(0, 0)$. Wakati graph mwanga wa ulinganifu, hakuna ulinganifu rasmi kuhusiana na kupita vipimo ulinganifu. Zaidi ya hayo, hakuna thamani ya juu, isipokuwa kikoa kizuizi.

Unda meza kama Jedwali$\PageIndex{9}$.

Jedwali$\PageIndex{9}$
$\theta$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$	$0.785$	$1.57$	$3.14$	$4.71$	$5.50$	$6.28$

Angalia kwamba maadili ya r ni fomu tu ya decimal ya angle iliyopimwa kwa radians. Tunaweza kuwaona kwenye grafu katika Kielelezo$\PageIndex{22}$.

Grafu ya archimedes' ond r=theta juu ya [0,2pi]. Inaanza katika asili na spirals nje katika kitanzi kimoja kinyume chake. Pointi (pi/4, pi/4), (pi/2, pi/2), (pi, pi), (5pi/4, 5pi/4), (7pi/4, pi/4), na (2pi, 2pi) ni alama. — Kielelezo$\PageIndex{22}$: ond Archimedes '

Uchambuzi

uwanja wa Curve hii polar ni$[ 0,2\pi ]$. Kwa ujumla, hata hivyo, uwanja wa kazi hii ni$(−\infty,\infty)$. Kuchora usawa wa ond ya Archimedes ni rahisi sana, ingawa picha inafanya kuonekana kama itakuwa ngumu.

Zoezi$\PageIndex{6}$

Mchoro grafu ya$r=−\theta$ zaidi ya muda$[ 0,4\pi ]$.

Jibu: $alt$
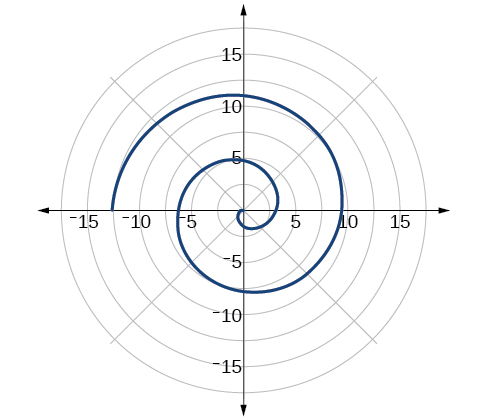
Kielelezo$\PageIndex{23}$

Muhtasari wa curves

Sisi kuchunguzwa idadi ya curves inaonekana tata polar katika sehemu hii. Kielelezo$\PageIndex{24}$ na Kielelezo$\PageIndex{25}$ muhtasari grafu na milinganyo kwa kila moja ya curves haya.

Grafu nne kwa upande - muhtasari. (A) ni mduara: r=asin (theta) au r=acos (theta). (B) ni cardioid: r= a + au - bcos (theta), au r = a + au - b dhambi (theta). a — Kielelezo$\PageIndex{24}$

Grafu nne kwa upande - muhtasari. (A) ni lemniscates. R ^ 2 = a ^ 2cos (2theta), au r ^ 2=a ^ 2sin (2theta). si sawa na 0. (B) ni rose Curve (n hata). R = acos (ntheta), au r=asin (ntheta). N ni hata, na kuna 2n petals. (C) ni rose Curve (n isiyo ya kawaida). R = acos (ntheta), au r=asin (theta). N ni isiyo ya kawaida, na hakuna petals. (D) ni ond Archimedes ya. R=Theta, na theta — Kielelezo$\PageIndex{25}$

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na grafu za kuratibu polar.

Graphing Polar equations sehemu ya 1
Graphing Polar equations sehemu ya 2
Uhuishaji: Grafu ya Ulinganisho wa Polar
Graphing Polar equations juu ya TI-84

Dhana muhimu

Ni rahisi kupiga milinganyo ya polar ikiwa tunaweza kupima equations kwa ulinganifu kwa heshima na mstari$\theta=\dfrac{\pi}{2}$, mhimili wa polar, au pole.
Kuna vipimo vitatu vya ulinganifu vinavyoonyesha kama grafu ya equation ya polar itaonyesha ulinganifu. Ikiwa equation inashindwa mtihani wa ulinganifu, grafu inaweza au isionyeshe ulinganifu. Angalia Mfano$\PageIndex{1}$.
Milinganyo ya polar inaweza kuwa graphed kwa kufanya meza ya maadili kwa$\theta$ na$r$.
Thamani ya juu ya equation ya polar inapatikana kwa kubadili thamani$\theta$ inayoongoza kwa thamani ya juu ya kujieleza trigonometric.
Zero za equation ya polar hupatikana kwa kuweka$r=0$ na kutatua$\theta$. Angalia Mfano$\PageIndex{2}$.
Baadhi ya formula zinazozalisha grafu ya mduara katika kuratibu za polar hutolewa$r=a \cos \theta$ na$r=a \sin \theta$. Angalia Mfano$\PageIndex{3}$.
Njia zinazozalisha grafu za cardioid hutolewa$r=a\pm b \cos \theta$ na$r=a\pm b \sin \theta$, kwa$a>0$,$b>0$, na$ab=1$. Angalia Mfano$\PageIndex{4}$.
Njia zinazozalisha grafu za limaçon moja ya kitanzi hutolewa$r=a\pm b \cos \theta$ na$r=a\pm b \sin \theta$ kwa$1<ab<2$. Angalia Mfano$\PageIndex{5}$.
Fomu zinazozalisha grafu za limaçon ya ndani ya kitanzi hutolewa$r=a\pm b \cos \theta$ na$r=a\pm b \sin \theta$$a>0$, na$b>0$, na$a<b$. Angalia Mfano$\PageIndex{6}$.
Fomula zinazozalisha grafu za lemniscates zinatolewa$r^2=a^2 \cos 2\theta$ na$r^2=a^2 \sin 2\theta$, wapi$a≠0$ .Angalia Mfano$\PageIndex{7}$.
formula kwamba kuzalisha grafu ya curves rose ni kutolewa$r=a \cos n\theta$ na na$r=a \sin n\theta$, ambapo$a≠0$; kama$n$ ni hata, kuna$2n$ petals, na kama$n$ ni isiyo ya kawaida, kuna n petals. Angalia Mfano$\PageIndex{8}$ na Mfano$\PageIndex{9}$.
Fomu inayozalisha grafu ya ond ya Archimedes inatolewa na$r=\theta$,$\theta≥0$. Angalia Mfano$\PageIndex{10}$.

\(\theta\)	\(r=2 \sin \theta\)	\(r\)
\ (\ theta\) ">\(0\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin(0)=0\)	\ (r\) ">\(0\)
\ (\ theta\) ">\(\dfrac{\pi}{6}\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{6}\right)=1\)	\ (r\) ">\(1\)
\ (\ theta\) ">\(\dfrac{\pi}{3}\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73\)	\ (r\) ">\(1.73\)
\ (\ theta\) ">\(\dfrac{pi}{2}\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{2}\right)=2\)	\ (r\) ">\(2\)
\ (\ theta\) ">\(\dfrac{2\pi}{3}\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73\)	\ (r\) ">\(1.73\)
\ (\ theta\) ">\(\dfrac{5\pi}{6}\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin\left(\dfrac{5\pi}{6}\right)=1\)	\ (r\) ">\(1\)
\ (\ theta\) ">\(\pi\)	\ (r=2\ dhambi\ theta\) ">\(r=2 \sin(\pi)=0\)	\ (r\) ">\(0\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)
\(r\)	\(4\)	\(3.46\)	\(2.83\)	\(2\)	\(0\)	\(−2\)	\(−2.83\)	\(−3.46\)	\(4\)

	0	\(\dfrac{π}{4}\)	\(\dfrac{π}{2}\)	\(\dfrac{2π}{3}\)	\(π\)
r	4	3.41	2	1	0

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(4\)	\(2.5\)	\(1.4\)	\(1\)	\(1.4\)	\(2.5\)	\(4\)	\(5.5\)	\(6.6\)	\(7\)	\(6.6\)	\(5.5\)	\(4\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(7\)	\(6.3\)	\(4.5\)	\(2\)	\(−0.5\)	\(−2.3\)	\(−3\)	\(−2.3\)	\(−0.5\)	\(2\)	\(4.5\)	\(6.3\)	\(7\)

Kumbuka: vipimo vya ulinganifu

Jinsi ya: Kutokana na equation polar, mtihani kwa ulinganifu.

Mfano\(\PageIndex{1}\): Testing a Polar Equation for Symmetry

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Finding Zeros and Maximum Values for a Polar Equation

Zoezi\(\PageIndex{2}\)

Kuchunguza miduara

FORMULA KWA EQUATION YA MDUARA

Mfano\(\PageIndex{3}\): Sketching the Graph of a Polar Equation for a Circle

Kuchunguza Cardioids

FORMULA KWA CARDIOID

Jinsi ya: Kutokana na equation ya polar ya cardioid, mchoro grafu yake

Mfano\(\PageIndex{4}\): Sketching the Graph of a Cardioid

Kuchunguza Limaçons

FORMULA KWA LIMAÇONS MOJA YA KITANZI

Jinsi ya: Kutokana na equation ya polar kwa limaçon moja ya kitanzi, mchoro grafu

Mfano\(\PageIndex{5}\): Sketching the Graph of a One-Loop Limaçon

Zoezi\(\PageIndex{3}\)

FORMULA KWA LIMAÇONS YA NDANI YA KITANZI

Mfano\(\PageIndex{6}\): Sketching the Graph of an Inner-Loop Limaçon

Kuchunguza Lemniscates

FORMULA KWA AJILI YA LEMNISCATES

Mfano\(\PageIndex{7}\): Sketching the Graph of a Lemniscate

Kuchunguza Rose Curves

ROSE CURVES

Mfano\(\PageIndex{8}\): Sketching the Graph of a Rose Curve (\(n\) Even)

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{9}\): Sketching the Graph of a Rose Curve (\(n\) Odd)

Zoezi\(\PageIndex{5}\)

Kuchunguza Spiral Archimedes '

OND ARCHIMEDES '

Jinsi ya: Kutokana na ond Archimedes 'juu\([ 0,2\pi ]\),sketch the graph

Mfano\(\PageIndex{10}\): Sketching the Graph of an Archimedes’ Spiral

Zoezi\(\PageIndex{6}\)

Media

\(\theta\)	\(0\)	\(\dfrac{\pi}{8}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{3\pi}{8}\)	\(\dfrac{\pi}{2}\)	\(5π8\)	\(3π4\)
\(r\)	\(2\)	\(0\)	\(−2\)	\(0\)	\(2\)	\(0\)	\(−2\)

Jedwali\(\PageIndex{9}\)
\(\theta\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\pi\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2\pi\)
\(r\)	\(0.785\)	\(1.57\)	\(3.14\)	\(4.71\)	\(5.50\)	\(6.28\)