5.R: Kazi za Trigonometric (Tathmini)

Last updated
Save as PDF

Page ID: 181390

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

5.1: Mazoezi ya Mapitio

Kwa mazoezi 1-2, kubadilisha hatua za angle kwa digrii.

1)$\dfrac{π}{4}$

Jibu: $45°$

2)$−\dfrac{5π}{3}$

Kwa mazoezi 3-6, kubadilisha hatua za angle kwa radians.

3)$-210°$

Jibu: $−\dfrac{7π}{6}$

4)$180°$

5) Kupata urefu wa arc katika mduara wa$7$ mita radius subtended na angle ya kati ya$85°$.

Jibu: $10.385$mita

6) Pata eneo la sekta ya mduara na$32$ miguu ya kipenyo na angle ya$\dfrac{3π}{5}$ radians.

Kwa mazoezi 7-8, pata angle kati$0°$ na$360°$ hiyo ni coterminal na angle iliyotolewa.

7)$420°$

Jibu: $60°$

8)$−80°$

Kwa mazoezi 9-10, pata angle kati$0$ na$2π$ katika radians ambayo ni coterminal na angle iliyotolewa.

9)$− \dfrac{20π}{11}$

Jibu: $\dfrac{2π}{11}$

10)$\dfrac{14π}{5}$

Kwa mazoezi 11-, futa angle iliyotolewa katika nafasi ya kawaida kwenye ndege ya Cartesian.

11)$-210°$

Jibu: $alt$

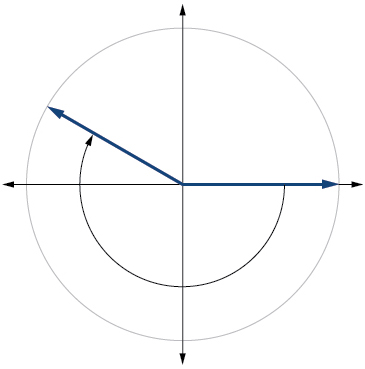
12)$75°$

13)$\dfrac{5π}{4}$

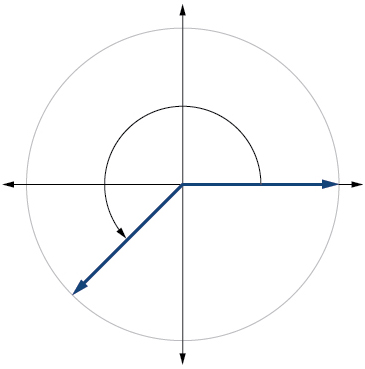
Jibu: $CNX_Precalc_Figure_05_04_219.jpg$

14)$−\dfrac{π}{3}$

15) Pata kasi ya mstari wa nukta kwenye ikweta ya dunia ikiwa dunia ina radius ya$3,960$ maili na dunia inazunguka kwenye mhimili wake kila$24$ masaa. Express jibu katika maili kwa saa.

Jibu: $1036.73$maili kwa saa

16) Gurudumu la gari na kipenyo cha$18$ inchi huzunguka kwa kiwango cha$10$ mapinduzi kwa pili. Kasi ya gari kwa maili kwa saa ni nini?

5.2: Mazoezi ya Mapitio

1) Kupata thamani halisi ya$ \sin \dfrac{π}{3}$.

Jibu: $\dfrac{\sqrt{3}}{2}$

2) Kupata thamani halisi ya$ \cos \dfrac{π}{4}$.

3) Kupata thamani halisi ya$ \cos π $.

Jibu: $-1$

4) Hali angle ya kumbukumbu kwa$300°$.

5) Hali angle ya kumbukumbu kwa$ \dfrac{3π}{4}$.

Jibu: $ \dfrac{π}{4}$

6) Compute cosine ya$330°$.

7) Kokotoa mstari wa$\dfrac{5π}{4}$.

Jibu: $−\dfrac{\sqrt{2}}{2}$

8) Weka uwanja wa kazi za sine na cosine.

9) Weka aina mbalimbali za kazi za sine na cosine.

Jibu: $[–1,1]$

5.3: Mazoezi ya Mapitio

Kwa mazoezi 1-4, pata thamani halisi ya maneno yaliyotolewa.

1)$ \cos \dfrac{π}{6} $

2)$ \tan \dfrac{π}{4} $

Jibu: $1$

3)$ \csc \dfrac{π}{3}$

4)$ \sec \dfrac{π}{4} $

Jibu: $\sqrt{2}$

Kwa mazoezi 4-12, tumia pembe za kumbukumbu ili kutathmini maneno yaliyotolewa.

5)$ \sec \dfrac{11π}{3}$

6)$ \sec 315°$

Jibu: $ \sqrt{2}$

7) Kama$ \sec (t)=−2.5$, ni nini$ \sec (−t)$?

8) Kama$ \tan (t)=−0.6 $, ni nini$ \tan (−t)$?

Jibu: $0.6$

9) Kama$ \tan (t)=\dfrac{1}{3}$, tafuta$ \tan (t−π)$.

10) Kama$ \cos (t)= \dfrac{\sqrt{2}}{2}$, kupata$ \sin (t+2π)$.

Jibu: $\dfrac{\sqrt{2}}{2}$au$−\dfrac{\sqrt{2}}{2}$

11) Ni kazi gani ya trigonometric ni hata?

12) Ni kazi gani ya trigonometric isiyo ya kawaida?

Jibu: mgongo, cosecant, tangent, cotangent

5.4: Mazoezi ya Mapitio

Kwa mazoezi 1-5, tumia urefu wa upande ili kutathmini.

1)$ \cos \dfrac{π}{4}$

2)$ \cot \dfrac{π}{3}$

Jibu: $\dfrac{\sqrt{3}}{3}$

3)$ \tan \dfrac{π}{6}$

4)$ \cos (\dfrac{π}{2}) = \sin ( \_\_°)$

Jibu: $0$

5)$ \csc (18°)= \sec (\_\_°)$

Kwa mazoezi 6-7, tumia taarifa iliyotolewa ili kupata urefu wa pande nyingine mbili za pembetatu sahihi.

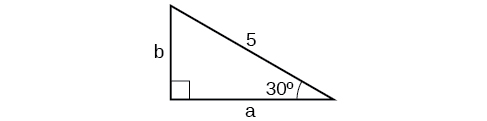
6)$ \cos B= \dfrac{3}{5}, a=6$

Jibu: $ b=8,c=10$

7)$ \tan A = \dfrac{5}{9},b=6 $

Kwa mazoezi 8-9, tumia Kielelezo hapa chini ili kutathmini kila kazi ya trigonometric.

$alt$

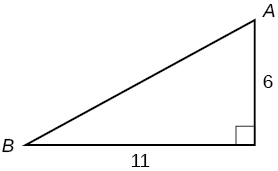
8)$ \sin A $

Jibu: $ \dfrac{11\sqrt{157}}{157}$

9)$ \tan B $

Kwa mazoezi 10-11, tatua kwa pande zisizojulikana za pembetatu iliyotolewa.

10)

$alt$

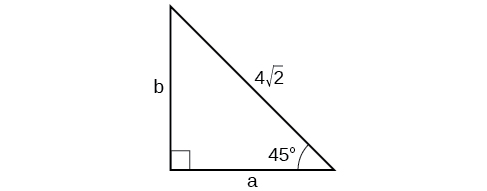
Jibu: $a=4, b=4 $

11)

$alt$

12) Ngazi$15$ -ft hutegemea jengo ili angle kati ya ardhi na ngazi ni$70°$. Je! Ngazi hiyo inafikia juu ya upande wa jengo?

Jibu: $14.0954$ft

13) Pembe ya mwinuko hadi juu ya jengo huko Baltimore inapatikana kuwa$4$ digrii kutoka chini kwa umbali wa$1$ maili kutoka msingi wa jengo hilo. Kutumia habari hii, pata urefu wa jengo.

Mazoezi mtihani

1) Badilisha$ \dfrac{5π}{6}$ radians kwa digrii.

Jibu: $150°$

2) Badilisha$−620°$ kwa radians.

3) Kupata urefu wa arc mviringo na$12$ sentimita radius subtended na angle ya kati ya$30°$.

Jibu: $6.283$sentimita

4) Pata eneo la sekta na radius ya$8$ miguu na angle ya$\dfrac{5π}{4}$ radians.

5) Kupata angle kati$0°$ na$360°$ kwamba ni coterminal na$375°$.

Jibu: $15°$

6) Kupata angle kati$0$ na$2π$ katika radians kwamba ni coterminal na$−\dfrac{4π}{7}$.

7) Chora angle$315°$ katika nafasi ya kawaida kwenye ndege ya Cartesian.

Jibu: $alt$

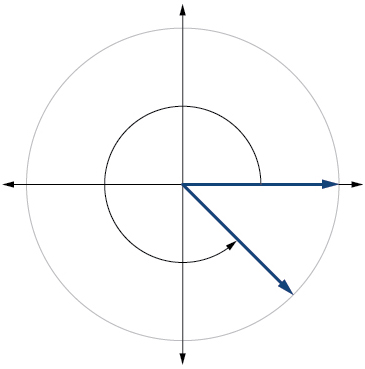
8) Chora angle$−\dfrac{π}{6}$ katika nafasi ya kawaida kwenye ndege ya Cartesian.

9) Carnival ina gurudumu la Ferris na kipenyo cha$80$ miguu. Wakati wa gurudumu la Ferris kufanya mapinduzi moja ni$75$ sekunde. ni linear kasi katika miguu kwa sekunde ya uhakika juu ya gurudumu Ferris nini? Je! Kasi ya angular katika radians kwa pili ni nini?

Jibu: $3.351$miguu kwa pili,$ \dfrac{2π}{75}$ radians kwa pili

10) Kupata thamani halisi ya$ \sin \dfrac{π}{6}$.

11) Kokotoa sine ya$240°$.

Jibu: $−\dfrac{\sqrt{3}}{2}$

12) Weka uwanja wa kazi za sine na cosine.

13) Weka aina mbalimbali za kazi za sine na cosine.

Jibu: $[ –1,1 ]$

14) Kupata thamani halisi ya$ \cot \dfrac{π}{4}$.

15) Kupata thamani halisi ya$ \tan \dfrac{π}{3}$.

Jibu: $ \sqrt{3}$

16) Tumia pembe za kumbukumbu ili kutathmini$ \csc \dfrac{7π}{4}$.

17) Tumia pembe za kumbukumbu ili kutathmini$ \tan 210°$.

Jibu: $\dfrac{\sqrt{3}}{3}$

18) Kama$ \csc t=0.68$, ni nini$ \csc (−t)$?

19) Kama$ \cos t= \dfrac{\sqrt{3}}{2}$, kupata$ \cos (t−2π)$.

Jibu: $\dfrac{\sqrt{3}}{2}$

20) Ni kazi gani za trigonometric ni hata?

21) Pata angle iliyopo:$\cos \left(\dfrac{\pi }{6} \right)= \sin (\;)$

Jibu: $\dfrac{π}{3}$

22) Pata pande zilizopo za pembetatu$ ABC: \sin B= \dfrac{3}{4},c=12$

23) Pata pande zilizopo za pembetatu.

$alt$

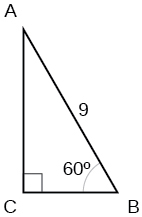
Jibu: $a=\dfrac{9}{2},b=\dfrac{9\sqrt{3}}{2}$

24) Angle ya mwinuko hadi juu ya jengo huko Chicago inapatikana kuwa$9$ digrii kutoka chini kwa umbali wa$2000$ miguu kutoka chini ya jengo hilo. Kutumia habari hii, pata urefu wa jengo.