7.4: Kutatua Tatizo
- Page ID
- 177285
Malengo ya kujifunza
- Eleza mikakati ya kutatua tatizo
- Eleza algorithm na heuristic
- Eleza baadhi ya barabarani ya kawaida ya kutatua tatizo
Watu wanakabiliwa na matatizo kila siku-kwa kawaida, matatizo mengi siku nzima. Wakati mwingine matatizo haya ni moja kwa moja: Ili mara mbili kichocheo cha unga wa pizza, kwa mfano, yote ambayo inahitajika ni kwamba kila kiungo katika mapishi kitaongezeka mara mbili. Wakati mwingine, hata hivyo, matatizo tunayokutana ni ngumu zaidi. Kwa mfano, kusema una tarehe ya mwisho ya kazi, na lazima barua nakala iliyochapishwa ya ripoti kwa msimamizi wako mwishoni mwa siku ya biashara. Ripoti hiyo ni nyeti wakati na inapaswa kutumwa mara moja. Umemaliza ripoti jana usiku, lakini printer yako haifanyi kazi leo. Unapaswa kufanya nini? Kwanza, unahitaji kutambua tatizo na kisha kutumia mkakati wa kutatua tatizo.
Mikakati ya kutatua matatizo
Wakati wewe ni iliyotolewa na tatizo-kama ni tata hisabati tatizo au printer kuvunjwa, jinsi gani kutatua hilo? Kabla ya kutafuta suluhisho la tatizo, tatizo lazima kwanza lieleweke wazi. Baada ya hapo, moja ya mikakati mingi ya kutatua tatizo inaweza kutumika, kwa matumaini kusababisha suluhisho.
Mkakati wa kutatua matatizo ni mpango wa utekelezaji unaotumiwa kupata suluhisho. Mikakati tofauti ina mipango tofauti ya utekelezaji inayohusishwa nao (Angalia Jedwali\(\PageIndex{1}\) hapa chini). Kwa mfano, mkakati maalumu ni jaribio na kosa. Neno la zamani, “Ikiwa kwa mara ya kwanza hufanikiwa, jaribu, jaribu tena” inaelezea jaribio na hitilafu. Kwa upande wa printer yako iliyovunjika, unaweza kujaribu kuangalia viwango vya wino, na ikiwa haifanyi kazi, unaweza kuangalia ili kuhakikisha tray ya karatasi haipatikani. Au labda printer haijaunganishwa kwenye kompyuta yako ya mbali. Unapotumia jaribio na hitilafu, utaendelea kujaribu ufumbuzi tofauti mpaka utatatua tatizo lako. Ingawa jaribio na hitilafu sio kawaida moja ya mikakati yenye ufanisi zaidi, ni moja ya kawaida kutumika.
| Mbinu | Maelezo | Mfano |
|---|---|---|
| Jaribio na hitilafu | Endelea kujaribu ufumbuzi tofauti mpaka tatizo litatatuliwa | Kuanzisha upya simu, kuzima WiFi, kuzima bluetooth ili kuamua kwa nini simu yako haifanyi kazi |
| Algorm | Fomu ya kutatua matatizo ya hatua kwa hatua | Mwongozo wa maelekezo ya kufunga programu mpya kwenye kompyuta yako |
| Heuristic | Mfumo wa jumla wa kutatua matatizo | Kufanya kazi nyuma; kuvunja kazi katika hatua |
Aina nyingine ya mkakati ni algorithm. Algorithm ni formula ya kutatua matatizo ambayo inakupa maelekezo ya hatua kwa hatua kutumika kufikia matokeo ya taka (Kahneman, 2011). Unaweza kufikiria algorithm kama kichocheo na maelekezo ya kina ambayo yanazalisha matokeo sawa kila wakati wanapofanyika. Algorithms hutumiwa mara kwa mara katika maisha yetu ya kila siku, hasa katika sayansi ya kompyuta. Unapoendesha utafutaji kwenye mtandao, inji za utafutaji kama Google hutumia algorithms ili kuamua ni vipi viingilio vitakavyoonekana kwanza katika orodha yako ya matokeo. Facebook pia hutumia algorithms kuamua ni machapisho gani ya kuonyesha kwenye habari zako. Je, unaweza kutambua hali nyingine ambazo algorithms hutumiwa?
Heuristic ni aina nyingine ya mkakati wa kutatua tatizo. Wakati algorithm inapaswa kufuatiwa hasa ili kuzalisha matokeo sahihi, heuristic ni mfumo wa kutatua matatizo ya jumla (Tversky & Kahneman, 1974). Unaweza kufikiria haya kama njia za mkato za akili ambazo hutumiwa kutatua matatizo. “Utawala wa kidole” ni mfano wa heuristic. Sheria hiyo inaokoa mtu wakati na nishati wakati wa kufanya uamuzi, lakini licha ya sifa zake za kuokoa muda, sio njia bora ya kufanya uamuzi wa busara. Aina tofauti za heuristics hutumiwa katika aina tofauti za hali, lakini msukumo wa kutumia heuristic hutokea wakati mojawapo ya masharti matano yamekutana (Pratkanis, 1989):
- Wakati mtu anakabiliwa na habari nyingi
- Wakati wa kufanya uamuzi ni mdogo
- Wakati uamuzi wa kufanywa ni muhimu
- Wakati kuna upatikanaji wa habari kidogo sana kutumia katika kufanya uamuzi
- Wakati heuristic sahihi hutokea kuja akilini katika wakati huo huo
Kufanya kazi nyuma ni heuristic muhimu ambayo huanza kutatua tatizo kwa kuzingatia matokeo ya mwisho. Fikiria mfano huu: Unaishi mnamo Washington, D.C. na umealikwa\(\text{4 PM}\) kwenye harusi saa Jumamosi huko Philadelphia. Kujua kwamba Interstate\(95\) huelekea kurejesha siku yoyote ya wiki, unahitaji kupanga njia yako na wakati wa kuondoka kwako ipasavyo. Ikiwa unataka kuwa katika huduma ya harusi na\(\text{3:30 PM}\), na inachukua\(2.5\) masaa ya kupata Philadelphia bila trafiki, ni wakati gani unapaswa kuondoka nyumbani kwako? Unatumia kazi ya nyuma ya heuristic kupanga matukio ya siku yako mara kwa mara, labda bila hata kufikiri juu yake.
Mwingine heuristic muhimu ni mazoezi ya kukamilisha lengo kubwa au kazi kwa kuivunja katika mfululizo wa hatua ndogo. Wanafunzi mara nyingi hutumia njia hii ya kawaida kukamilisha mradi mkubwa wa utafiti au insha ndefu kwa shule. Kwa mfano, wanafunzi kawaida kutafakari, kuendeleza Thesis au mada kuu, utafiti mada waliochaguliwa, kuandaa taarifa zao katika muhtasari, kuandika rasimu mbaya, kurekebisha na hariri rasimu mbaya, kuendeleza rasimu ya mwisho, kuandaa orodha ya marejeo, na kuthibitisha kazi zao kabla ya kugeuka katika mradi huo. Kazi kubwa inakuwa chini ya balaa wakati imevunjika katika mfululizo wa hatua ndogo.
EVERYDAY CONNECTION: Solving Puzzles
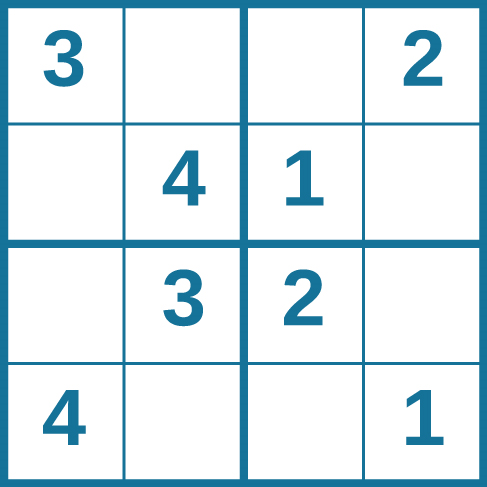
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a \(9\times 9\) grid. The simple sudoku below is a \(4\times 4\) grid. To solve the puzzle, fill in the empty boxes with a single digit: \(1\), \(2\), \(3\), or \(4\). Here are the rules: The numbers must total \(10\) in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.
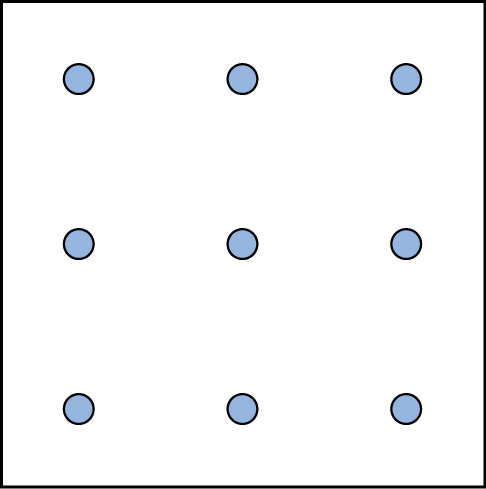
Here is another popular type of puzzle that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:
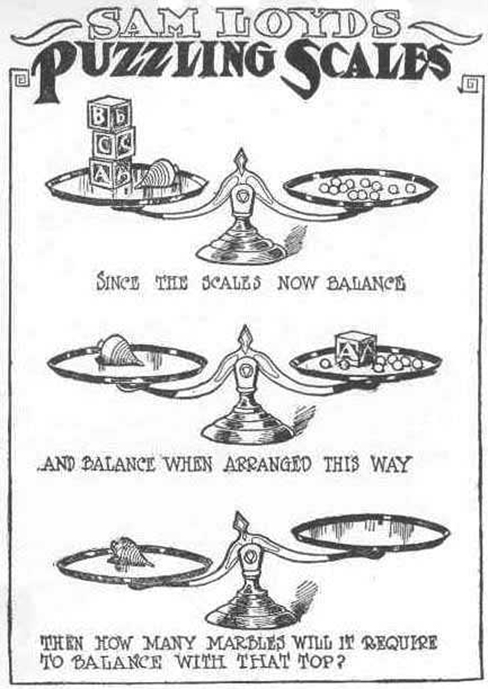
Take a look at the “Puzzling Scales” logic puzzle below. Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).
Pitfalls to Problem Solving
Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.
Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.
Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).
In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of \(\$1,600\). The realtor shows you only very run-down houses for \(\$1,600\) and then shows you a very nice house for \(\$2,000\). Might you ask each person to pay more in rent to get the \(\$2,000\) home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.
The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.
Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision. Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the Table \(\PageIndex{2}\) below.
| Bias | Description |
|---|---|
| Anchoring | Tendency to focus on one particular piece of information when making decisions or problem-solving |
| Confirmation | Focuses on information that confirms existing beliefs |
| Hindsight | Belief that the event just experienced was predictable |
| Representative | Unintentional stereotyping of someone or something |
| Availability | Decision is based upon either an available precedent or an example that may be faulty |
Were you able to determine how many marbles are needed to balance the scales in Figure \(\PageIndex{3}\)? You need nine.
Were you able to solve the problems in Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\)? Here are the answers:
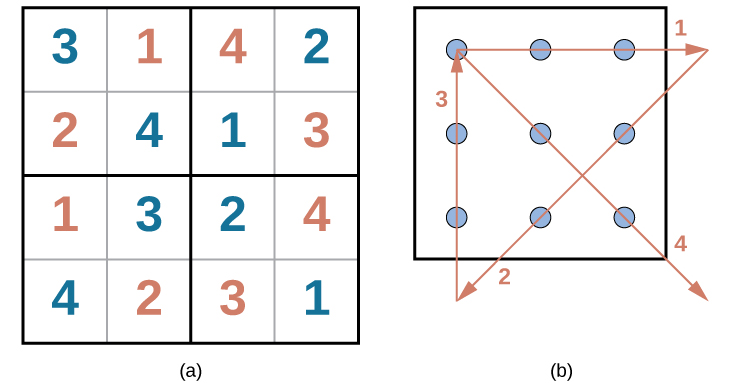
Figure \(\PageIndex{4}\): Solutions to the puzzles in Everyday Connection
Summary
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.
Glossary
- algorithm
- problem-solving strategy characterized by a specific set of instructions
- anchoring bias
- faulty heuristic in which you fixate on a single aspect of a problem to find a solution
- availability heuristic
- faulty heuristic in which you make a decision based on information readily available to you
- confirmation bias
- faulty heuristic in which you focus on information that confirms your beliefs
- functional fixedness
- inability to see an object as useful for any other use other than the one for which it was intended
- heuristic
- mental shortcut that saves time when solving a problem
- hindsight bias
- belief that the event just experienced was predictable, even though it really wasn’t
- mental set
- continually using an old solution to a problem without results
- problem-solving strategy
- method for solving problems
- representative bias
- faulty heuristic in which you stereotype someone or something without a valid basis for your judgment
- trial and error
- problem-solving strategy in which multiple solutions are attempted until the correct one is found
- working backwards
- heuristic in which you begin to solve a problem by focusing on the end result


