10.5: Kasi ya Angular na Uhifadhi wake
- Page ID
- 183784
Malengo ya kujifunza
Mwishoni mwa sehemu hii, utaweza:
- Kuelewa mlinganisho kati ya kasi ya angular na kasi ya mstari.
- Angalia uhusiano kati ya kasi na kasi ya angular.
- Tumia sheria ya uhifadhi wa kasi ya angular.
Kwa nini Dunia inaendelea kugeuka? Nini ilianza inazunguka kuanza na? Na skater ya barafu inawezaje kuzunguka kwa kasi na kwa kasi tu kwa kuvuta mikono yake ndani? Kwa nini yeye hawana haja ya kutumia muda wa kuzunguka kwa kasi? Maswali kama haya yana majibu kulingana na kasi ya angular, Analog ya mzunguko kwa kasi ya mstari.
Kwa sasa mfano ni wazi-kila jambo la mzunguko lina analog ya moja kwa moja ya kutafsiri. Inaonekana busara kabisa, basi, kufafanua kasi angular\(L\) kama\[L = I\omega\]
Equation hii ni Analog kwa ufafanuzi wa kasi linear kama
\[p = mv\]
Units kwa kasi linear ni\(kg \cdot m/s\), wakati vitengo kwa kasi angular ni\(kg \cdot m/s^2\). Kama tunavyotarajia, kitu ambacho kina muda mkubwa wa inertia\(I\), kama vile Dunia, kina kasi kubwa sana ya angular. Kitu kilicho na kasi kubwa ya angular\(\omega\), kama vile centrifuge, pia kina kasi kubwa ya angular.
Kasi ya angular ni sawa kabisa na kasi ya mstari, kwanza iliyotolewa katika Uniform Circular Motion na Gravitation. Ina maana sawa katika suala la kubeba mzunguko mbele, na huhifadhiwa wakati moment ya nje ya nje ni sifuri. Kasi ya angular, kama kasi ya mstari, pia ni mali ya atomi na chembe za subatomiki.
Mfano\(\PageIndex{1}\): Calculating Angular Momentum of the Earth
Je! Ni kasi gani ya angular ya dunia?
Mkakati
Hakuna taarifa iliyotolewa katika taarifa ya tatizo; kwa hiyo tunapaswa kuangalia data muhimu kabla ya kuhesabu\(L = I\omega\) Kwanza, formula kwa wakati wa inertia ya nyanja ni
\[I = \dfrac{2MR^2}{5}\]ili
\[L = I\omega = \dfrac{2MR^2\omega}{5}.\]
Masi ya dunia\(M\) ni\(5.979 \times 10^{24} \, kg\) na radius yake\(R\) ni\(6.376 \times 10^6 \, m\). Kasi ya angular ya Dunia\(\omega\) ni, bila shaka, mapinduzi moja kwa siku, lakini ni lazima tujifunze\(\omega\) kwa radians kwa sekunde ili kufanya hesabu katika vitengo vya SI.
Suluhisho
Kubadilisha habari inayojulikana katika usemi kwa\(L\) na kugeuza\(\omega\) kwa radians kwa sekunde anatoa
\[L = 0.4(5.979 \times 10^{24} \, kg)(6.376 \times 10^6 \, m)\left(\dfrac{1 \, rev}{d}\right)\]
\[= 9.72 \times 10^{37} \, kg \cdot m^2 \cdot rev/d\]
Kubadilisha\(2\pi\) kwa rev 1 na\(8.64 \times 10^4 \, s\) kwa siku 1 inatoa
\[L = (9.72 \times 10^{37} \, kg \cdot m^2)\left(\dfrac{2\pi \, rad/rev}{8.64 \times 10^4 \, s/d}\right) (1 \, rev/d)\]
\[= 7.07 \times 10^{33} \, kg \cdot m^2/s.\]
Majadiliano
Nambari hii ni kubwa, inayoonyesha kwamba Dunia, kama inavyotarajiwa, ina kasi kubwa ya angular. Jibu ni takriban, kwa sababu tumefikiri wiani wa mara kwa mara kwa Dunia ili kukadiria wakati wake wa inertia.
Wakati kushinikiza merry-kwenda pande zote, spin gurudumu baiskeli, au kufungua mlango, wewe exert moment. Ikiwa wakati unayofanya ni mkubwa zaidi kuliko kupinga torques, basi mzunguko huharakisha, na ongezeko la angular huongezeka. Zaidi ya kasi ya wavu, ongezeko la haraka zaidi\(L\). Uhusiano kati ya kasi na kasi ya angular ni
\[net \, \tau = \dfrac{\Delta L}{\Delta t}.\]
Maneno haya ni sawa na uhusiano kati ya nguvu na kasi ya mstari,\(F = \Delta p/\Delta t\). Equation\(net \, \tau = \Delta L/ \Delta t\) ni ya msingi sana na inatumika kwa upana. Kwa kweli, aina ya mzunguko wa sheria ya pili ya Newton.
Mfano\(\PageIndex{1}\): Calculating the Torque Putting Angular Momentum Into a Lazy Susan
Kielelezo\(\PageIndex{1}\) inaonyesha wavivu Susan chakula tray kuwa kuzungushwa na mtu katika jitihada ya riziki. Tuseme mtu huyo ana nguvu ya 2.50 N perpendicular kwa radius wavivu Susan ya 0.260-m kwa 0.150 s.
- Je, ni mwisho angular kasi ya Susan wavivu kama ni kuanza kutoka mapumziko, kuchukua msuguano ni kidogo?
- Je, ni kasi ya mwisho ya angular ya Susan wavivu, kutokana na kwamba uzito wake ni kilo 4.00 na kuchukua muda wake wa inertia ni ile ya disk?
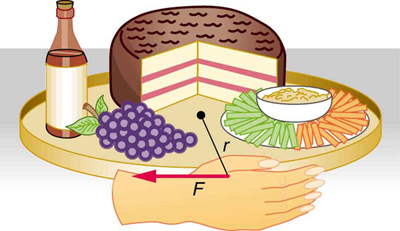
Kielelezo\(\PageIndex{1}\): partygoer exerts moment juu Susan wavivu kufanya hivyo mzunguko. Equation\(net \, \tau = \dfrac{\Delta L}{\Delta t}\) inatoa uhusiano kati ya moment na kasi angular zinazozalishwa.
Mkakati
Tunaweza kupata kasi ya angular kwa kutatua\(net \, \tau = \dfrac{\Delta L}{\Delta t}\) for \(\Delta L\), and using the given information to calculate the torque. The final angular momentum equals the change in angular momentum, because the lazy Susan starts from rest. That is, \(\Delta L = L\) To find the final velocity, we must calculate \(\omega\) from the definition of \(L\) in \(L = I\omega\).
Solution for (a)
Solving \(net \, \tau = \dfrac{\Delta L}{\Delta t}\) for \(\Delta L\) gives
\[\Delta L = (net \, \tau)\Delta t.\]
Because the force is perpendicular to \(r\), we see that \(net \, \tau = rF\) so that
\[L = rF\Delta t = (0.260 \, m)(2.50 \, N)(0.150 \, s)\]
\[= 9.75 \times 10^{-2} \, kg \cdot m^2 /s.\]
Solution for (b)
The final angular velocity can be calculated from the definition of angular momentum,
\[L = I\omega.\]
Solving for \(\omega\) and substituting the formula for the moment of inertia of a disk into the resulting equation gives
\[\omega = \dfrac{L}{I} = \dfrac{L}{\dfrac{1}{2}MR^2}.\]
And substituting known values into the preceding equation yields
\[\omega = \dfrac{9.75 \times 10^{-2} \, kg \cdot m^2 /s}{(0.500)(4.00 \, kg)(0.260 \, m)} = 0.721 \, rad/s.\]
Discussion
Note that the imparted angular momentum does not depend on any property of the object but only on torque and time. The final angular velocity is equivalent to one revolution in 8.71 s (determination of the time period is left as an exercise for the reader), which is about right for a lazy Susan.
Example \(\PageIndex{3}\): Calculating the Torque in a Kick
The person whose leg is shown in \(\PageIndex{1}\) kicks his leg by exerting a 2000-N force with his upper leg muscle. The effective perpendicular lever arm is 2.20 cm. Given the moment of inertia of the lower leg is \(1.25 \, kg \cdot m^2\).
- find the angular acceleration of the leg.
- Neglecting the gravitational force, what is the rotational kinetic energy of the leg after it has rotated through \(57.3^0\) (1.00 rad)?
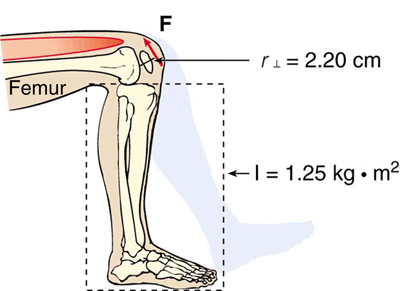
Strategy
The angular acceleration can be found using the rotational analog to Newton’s second law, or \(\alpha = net \, \tau/I\). The moment of inertia \(I\) is given and the torque can be found easily from the given force and perpendicular lever arm. Once the angular acceleration \(\alpha\) is known, the final angular velocity and rotational kinetic energy can be calculated.
Solution to (a)
From the rotational analog to Newton’s second law, the angular acceleration \(\alpha\) is
\[\alpha = \dfrac{net \, \tau}{I}.\]
Because the force and the perpendicular lever arm are given and the leg is vertical so that its weight does not create a torque, the net torque is thus
\[net \, \tau = r_{\perp}F\]
\[= (0.0220 \, m)(2000 \, N)\]
\[= 44.0 \, N \cdot m\]
Substituting this value for the torque and the given value for the moment of inertia into the expression for \(\alpha\) gives
\[\alpha = \dfrac{44.0 \, N\cdot m}{1.25 \, kg \cdot m^2} = 35.2 \, rad/s^2\]
Solution to (b)
The final angular velocity can be calculated from the kinematic expression
\[\omega^2 = \omega_0^2 + 2\alpha \theta\]
or
\[\omega^2 = 2\alpha \theta\]
because the initial angular velocity is zero. The kinetic energy of rotation is
\[KE_{rot} = \dfrac{1}{2}I \omega^2\]
so it is most convenient to use the value of \(\omega^2\) just found and the given value for the moment of inertia. The kinetic energy is then
\[KE_{rot}= 0.5(1.25 \, kg \cdot m^2)(70.4 \, rad^2/s^2)\]
\[= 44 \, J\]
Discussion
These values are reasonable for a person kicking his leg starting from the position shown. The weight of the leg can be neglected in part (a) because it exerts no torque when the center of gravity of the lower leg is directly beneath the pivot in the knee. In part (b), the force exerted by the upper leg is so large that its torque is much greater than that created by the weight of the lower leg as it rotates. The rotational kinetic energy given to the lower leg is enough that it could give a ball a significant velocity by transferring some of this energy in a kick.
Angular momentum, like energy and linear momentum, is conserved. This universally applicable law is another sign of underlying unity in physical laws. Angular momentum is conserved when net external torque is zero, just as linear momentum is conserved when the net external force is zero.
Conservation of Angular Momentum
We can now understand why Earth keeps on spinning. As we saw in the previous example, \(\Delta L = (net \, \tau)\Delta t\). This equation means that, to change angular momentum, a torque must act over some period of time. Because Earth has a large angular momentum, a large torque acting over a long time is needed to change its rate of spin. So what external torques are there? Tidal friction exerts torque that is slowing Earth’s rotation, but tens of millions of years must pass before the change is very significant. Recent research indicates the length of the day was 18 h some 900 million years ago. Only the tides exert significant retarding torques on Earth, and so it will continue to spin, although ever more slowly, for many billions of years.
What we have here is, in fact, another conservation law. If the net torque is zero, then angular momentum is constant or conserved. We can see this rigorously by considering \(net \, \tau = \dfrac{\Delta L}{\Delta t}\) for the situation in which the net torque is zero. In that case,
\[net \, \tau = 0\] implying that
\[\dfrac{\Delta L}{\Delta t} = 0.\]
If the change in angular momentum \(\Delta L\) is zero, then the angular momentum is constant; thus,
\[L = constant \, (net \, \tau = 0)\] or
\[L = L'(net \, \tau = 0).\]
These expressions are the law of conservation of angular momentum. Conservation laws are as scarce as they are important.
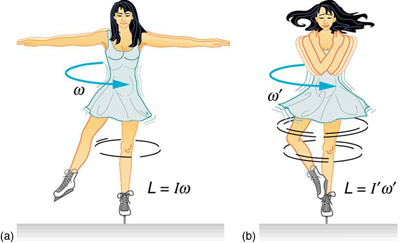
An example of conservation of angular momentum is seen in Figure \(\PageIndex{3}\), in which an ice skater is executing a spin. The net torque on her is very close to zero, because there is relatively little friction between her skates and the ice and because the friction is exerted very close to the pivot point. (Both \(F\) and \(\tau\) are small, and so \(\tau\) is negligibly small.) Consequently, she can spin for quite some time. She can do something else, too. She can increase her rate of spin by pulling her arms and legs in. Why does pulling her arms and legs in increase her rate of spin? The answer is that her angular momentum is constant, so that
\[L = L'.\]
Expressing this equation in terms of the moment of inertia,
\[I\omega = I'\omega'\]
where the primed quantities refer to conditions after she has pulled in her arms and reduced her moment of inertia. Because \(I'\) is smaller, the angular velocity \(\omega'\) must increase to keep the angular momentum constant. The change can be dramatic, as the following example shows.
Example \(\PageIndex{4}\): Calculating the Angular Momentum of a Spinning Skater
Suppose an ice skater, such as the one in Figure \(\PageIndex{3}\), is spinning at 0.800 rev/ s with her arms extended. She has a moment of inertia of \(2.34 \, kg \cdot m^2\) with her arms extended and of \(0.363 \, kg \cdot m^2\) with her arms close to her body. (These moments of inertia are based on reasonable assumptions about a 60.0-kg skater.) (a) What is her angular velocity in revolutions per second after she pulls in her arms? (b) What is her rotational kinetic energy before and after she does this?
Strategy
In the first part of the problem, we are looking for the skater’s angular velocity \(\omega'\) after she has pulled in her arms. To find this quantity, we use the conservation of angular momentum and note that the moments of inertia and initial angular velocity are given. To find the initial and final kinetic energies, we use the definition of rotational kinetic energy given by
\[KE_{rot} = \dfrac{1}{2} I\omega^2\]
Solution for (a)
Because torque is negligible (as discussed above), the conservation of angular momentum given in \(I\omega = I'\omega'\) is applicable. Thus,
\[L = L'\] or \[I\omega^2 = I'\omega'\]
Solving for \(\omega'\) and substituting known values into the resulting equation gives
\[\omega' = \dfrac{I}{I'}\omega = \left(\dfrac{2.34 \, kg \cdot m^2}{0.363 \, kg \cdot m^2} \right)(0.800 \, rev/s)\]
\[= 5.16 rev/s.\]
Solution for (b)
Rotational kinetic energy is given by
\[KE_{rot} = \dfrac{1}{2}I\omega^2\]
The initial value is found by substituting known values into the equation and converting the angular velocity to rad/s:
\[KE_{rot} = (0.5)(2.34 \, kg \cdot m^2)((0.800 \, rev/s)(2\pi \, rad/rev))^2\]
\[= 29.6 \, J.\]
The final rotational kinetic energy is
\[KE_{rot}' = \dfrac{1}{2}I'\omega^{'2}\]
Substituting known values into this equation gives
\[KE_{rot}' = (0.5)(0.363 \, kg \cdot m^2)[(5.16 \, rev/s)((2\pi \, rad/rev)]^2\]
\[= 191 \, J.\]
Discussion
In both parts, there is an impressive increase. First, the final angular velocity is large, although most world-class skaters can achieve spin rates about this great. Second, the final kinetic energy is much greater than the initial kinetic energy. The increase in rotational kinetic energy comes from work done by the skater in pulling in her arms. This work is internal work that depletes some of the skater’s food energy.
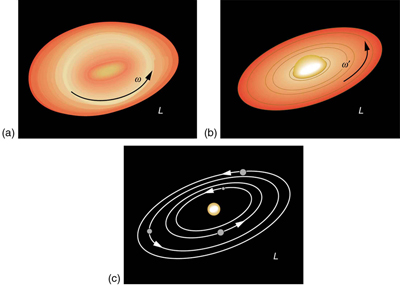
There are several other examples of objects that increase their rate of spin because something reduced their moment of inertia. Tornadoes are one example. Storm systems that create tornadoes are slowly rotating. When the radius of rotation narrows, even in a local region, angular velocity increases, sometimes to the furious level of a tornado. Earth is another example. Our planet was born from a huge cloud of gas and dust, the rotation of which came from turbulence in an even larger cloud. Gravitational forces caused the cloud to contract, and the rotation rate increased as a result (Figure \(\PageIndex{3}\)).
Exercise \(\PageIndex{1}\): Check Your Undestanding
Is angular momentum completely analogous to linear momentum? What, if any, are their differences?
Solution
Yes, angular and linear momenta are completely analogous. While they are exact analogs they have different units and are not directly inter-convertible like forms of energy are.
Summary
- Every rotational phenomenon has a direct translational analog , likewise angular momentum \(L\) can be defined as \(L = I\omega\).
- This equation is an analog to the definition of linear momentum as \(p = mv\). The relationship between torque and angular momentum is \(net \, \tau = \Delta L/\Delta t\).
- Angular momentum, like energy and linear momentum, is conserved. This universally applicable law is another sign of underlying unity in physical laws. Angular momentum is conserved when net external torque is zero, just as linear momentum is conserved when the net external force is zero.
Glossary
- angular momentum
- the product of moment of inertia and angular velocity
- law of conservation of angular momentum
- angular momentum is conserved, i.e., the initial angular momentum is equal to the final angular momentum when no external torque is applied to the system


