11.2: Mifumo ya Ulinganisho wa Mstari na Vigezo vitatu

Malengo ya kujifunza

• Tatua mifumo ya equations tatu katika vigezo vitatu.
• Tambua mifumo isiyoendana ya milinganyo iliyo na vigezo vitatu.
• Eleza suluhisho la mfumo wa equations tegemezi iliyo na vigezo vitatu.

Yohana alipokea urithi wa\($12,000\) ule aliogawanyika katika sehemu tatu na kuwekeza kwa njia tatu: katika mfuko wa soko la fedha kulipa riba ya\(3\%\) kila mwaka; katika vifungo vya manispaa kulipa riba ya\(4\%\) kila mwaka; na katika fedha za pamoja kulipa riba ya\(7\%\) kila mwaka. John imewekeza\($4,000\) zaidi katika fedha za manispaa kuliko vifungo vya manispaa. Alipata\($670\) kwa riba mwaka wa kwanza. John aliwekeza kiasi gani katika kila aina ya mfuko?

Kielelezo\(\PageIndex{1}\): (mikopo: “Elembis,” Wikimedia Commons)

Kuelewa mbinu sahihi ya kuanzisha matatizo kama hii hufanya kutafuta suluhisho suala la kufuata mfano. Tutatatua matatizo haya na yanayofanana yanayohusisha milinganyo mitatu na vigezo vitatu katika sehemu hii. Kufanya hivyo hutumia mbinu sawa na zile zinazotumiwa kutatua mifumo ya equations mbili katika vigezo viwili. Hata hivyo, kutafuta ufumbuzi wa mifumo ya equations tatu inahitaji shirika kidogo zaidi na kugusa kwa gymnastics ya kuona.

Kutatua Mifumo ya Equations Tatu katika Vigezo vitatu

Ili kutatua mifumo ya milinganyo katika vigezo vitatu, inayojulikana kama mifumo mitatu na mitatu, chombo cha msingi tutakayotumia kinaitwa kuondoa Gaussia, jina lake baada ya mtaalamu wa hisabati wa Ujerumani Karl Friedrich Gauss. Ingawa hakuna utaratibu wa uhakika ambao shughuli zitafanywa, kuna miongozo maalum kuhusu aina gani ya hatua zinaweza kufanywa. Tunaweza namba equations kuweka wimbo wa hatua tunazoomba. Lengo ni kuondoa variable moja kwa wakati ili kufikia fomu ya juu ya triangular, fomu bora kwa mfumo wa tatu na tatu kwa sababu inaruhusu kwa moja kwa moja nyuma badala ya kupata suluhisho\((x,y,z)\), ambayo tunaita amri tatu. Mfumo katika fomu ya juu ya triangular inaonekana kama yafuatayo:

\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]

equation tatu inaweza kutatuliwa kwa\(z\), na kisha sisi nyuma-mbadala ya kupata\(y\) na\(x\). Kuandika mfumo katika fomu ya juu ya triangular, tunaweza kufanya shughuli zifuatazo:

1. Kubadilishana utaratibu wa equations yoyote mbili.
2. Kuzidisha pande zote mbili za equation na mara kwa mara nonzero.
3. Kuongeza nonzero nyingi ya equation moja kwa equation mwingine.

Suluhisho lililowekwa kwenye mfumo wa tatu na tatu ni mara tatu iliyoamriwa\({(x,y,z)}\). Kwa mfano, mara tatu iliyoamriwa inafafanua hatua ambayo ni makutano ya ndege tatu katika nafasi. Unaweza kutazama makutano hayo kwa kufikiria kona yoyote katika chumba cha mstatili. Kona inaelezwa na ndege tatu: kuta mbili zinazojumuisha na sakafu (au dari). Hatua yoyote ambapo kuta mbili na sakafu hukutana inawakilisha makutano ya ndege tatu.

IDADI YA UFUMBUZI IWEZEKANAVYO

Kielelezo\(\PageIndex{2}\) na Kielelezo\(\PageIndex{3}\) kuonyesha uwezekano ufumbuzi matukio kwa ajili ya mifumo ya tatu na tatu.

• Mifumo iliyo na suluhisho moja ni yale ambayo, baada ya kukomesha, husababisha kuweka suluhisho linalojumuisha mara tatu zilizoamriwa\({(x,y,z)}\). Kwa mfano, mara tatu iliyoamriwa inafafanua hatua ambayo ni makutano ya ndege tatu katika nafasi.
• Mifumo ambayo ina idadi isiyo na kipimo ya ufumbuzi ni wale ambao, baada ya kuondoa, husababisha maneno ambayo daima ni kweli, kama vile\(0=0\). Graphically, idadi isiyo na kipimo ya ufumbuzi inawakilisha mstari au ndege coincident ambayo hutumika kama makutano ya ndege tatu katika nafasi.
• Mifumo isiyo na suluhisho ni yale ambayo, baada ya kuondoa, husababisha taarifa ambayo ni kinyume, kama vile\(3=0\). Graphically, mfumo usio na suluhisho unawakilishwa na ndege tatu bila uhakika sawa.

Kielelezo\(\PageIndex{2}\): (a) Ndege tatu zinaingiliana kwa hatua moja, inayowakilisha mfumo wa tatu na tatu na suluhisho moja. (b) Ndege tatu zinaingiliana kwenye mstari, zinazowakilisha mfumo wa tatu na tatu na ufumbuzi usio na mwisho.

Kielelezo\(\PageIndex{3}\): Takwimu zote tatu zinawakilisha mifumo mitatu na mitatu bila ufumbuzi. (a) Ndege tatu zinakabiliana, lakini si kwa kawaida. (b) Ndege mbili ni sawa na zinakabiliana na ndege ya tatu, lakini si kwa kila mmoja. (c) Ndege zote tatu ni sambamba, kwa hiyo hakuna hatua ya makutano.

Mfano\(\PageIndex{1}\): Determining Whether an Ordered Triple Is a Solution to a System

Kuamua kama mara tatu zilizoamriwa\((3,−2,1)\) ni suluhisho la mfumo.

\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]

Suluhisho

Sisi kuangalia kila equation kwa kubadilisha katika maadili ya kuamuru mara tatu kwa\( x,y\), na\(z\).

\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1)=2 \nonumber \\[4pt] \text{True}} & {6x−4y+5z=31 \nonumber \\[4pt] 6(3)−4(−2)+5(1)=31 \nonumber \\[4pt] 18+8+5=31 \nonumber \\[4pt] \text{True} } & { 5x+2y+2z = 13 \nonumber \\[4pt] 5(3)+2(−2)+2(1)=13 \nonumber \\[4pt] 15−4+2=13 \nonumber \\[4pt] \text{True}} \end{array}\]

Mara tatu iliyoamriwa\((3,−2,1)\) ni kweli suluhisho la mfumo.

Jinsi ya: Kutokana na mfumo wa mstari wa milinganyo mitatu, tatua kwa haijulikani tatu

1. Pick jozi yoyote ya equations na kutatua kwa variable moja.
2. Pick jozi nyingine ya equations na kutatua kwa variable huo.
3. Umeunda mfumo wa equations mbili katika haijulikani mbili. Tatua mfumo wa mbili-na-mbili.
4. Back-mbadala inayojulikana vigezo katika moja yoyote ya milinganyo ya awali na kutatua kwa kutofautiana kukosa.

Mfano\(\PageIndex{2}\): Solving a System of Three Equations in Three Variables by Elimination

Pata suluhisho la mfumo wafuatayo:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \nonumber \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]

Suluhisho

Kutakuwa na uchaguzi kadhaa kuhusu wapi kuanza, lakini hatua ya kwanza ya dhahiri hapa ni kuondokana\(x\) na kuongeza equations (1) na (2).

\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]

Hatua ya pili ni kuzidisha equation (1)\(−2\) na kuongeza matokeo kwa equation (3). Hatua hizi mbili zitaondoa kutofautiana\(x\).

\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ multiplied by }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]

Katika equations (4) na (5), tumeunda mfumo mpya wa mbili-na-mbili. Tunaweza kutatua\(z\) kwa kuongeza equations mbili.

\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \nonumber \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]

Kuchagua equation moja kutoka kila mfumo mpya, tunapata fomu ya juu ya triangular:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \nonumber \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]

Kisha, sisi nyuma mbadala\(z=2\) katika equation (4) na kutatua kwa\(y\).

\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]

Hatimaye, tunaweza nyuma-mbadala\(z=2\) na\(y=−1\) katika equation (1). Hii itazaa ufumbuzi kwa\(x\).

\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]

Suluhisho ni mara tatu iliyoamriwa\((1,−1,2)\). Angalia Kielelezo\(\PageIndex{4}\).

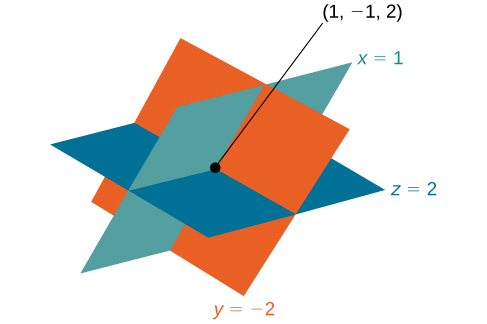
Kielelezo\(\PageIndex{4}\)

Mfano\(\PageIndex{3}\): Solving a Real-World Problem Using a System of Three Equations in Three Variables

Katika tatizo lililofanywa mwanzoni mwa sehemu hiyo, John aliwekeza urithi wake wa\($12,000\) fedha tatu tofauti: sehemu katika mfuko wa soko la fedha kulipa\(3\%\) riba kila mwaka; sehemu katika vifungo vya manispaa kulipa\(4\%\) kila mwaka; na wengine katika fedha za kuheshimiana kulipa\(7\%\) kila mwaka. John imewekeza\($4,000\) zaidi katika fedha za pamoja kuliko yeye imewekeza katika vifungo manispaa. Maslahi ya jumla yaliyopatikana kwa mwaka mmoja ilikuwa\($670\). Je! Aliwekeza kiasi gani katika kila aina ya mfuko?

Suluhisho

Ili kutatua tatizo hili, tunatumia habari zote zilizotolewa na kuanzisha equations tatu. Kwanza, sisi hawawajui variable kwa kila moja ya tatu kiasi uwekezaji:

\[\begin{align} x &= \text{amount invested in money-market fund} \nonumber \\[4pt] y &= \text{amount invested in municipal bonds} \nonumber \\[4pt] z &= \text{amount invested in mutual funds} \nonumber \end{align} \nonumber\]

equation kwanza inaonyesha kwamba jumla ya kiasi kuu tatu ni\($12,000\).

\[x+y+z=12,000 \nonumber\]

Tunaunda equation ya pili kulingana na taarifa kwamba John imewekeza\($4,000\) zaidi katika fedha kuheshimiana kuliko yeye imewekeza katika vifungo manispaa.

\[z=y+4,000 \nonumber\]

Ulinganisho wa tatu unaonyesha kwamba jumla ya riba inayotokana na kila mfuko ni sawa\($670\).

\[0.03x+0.04y+0.07z=670 \nonumber\]

Kisha, tunaandika equations tatu kama mfumo.

\[\begin{align} x+y+z &=12,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \\[4pt] 0.03x+0.04y+0.07z &= 670 \nonumber \end{align} \nonumber\]

Kufanya mahesabu rahisi, tunaweza kuzidisha equation ya tatu na\(100\). Hivyo,

\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4,000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67,000 \; &(3) \nonumber \end{align} \nonumber\]

Hatua ya 1. Interchange equation (2) na equation (3) ili equations mbili na vigezo tatu itakuwa line up.

\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] 3x+4y+7z &= 67,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

Hatua ya 2. Kuzidisha equation (1)\(−3\) na na kuongeza equation (2). Andika matokeo kama mstari wa 2.

\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

Hatua ya 3. Ongeza equation (2) kwa equation (3) na uandike matokeo kama equation (3).

\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] 5z &= 35,000 \nonumber \end{align} \nonumber\]

Hatua ya 4. Kutatua kwa\(z\) katika equation (3). Back-mbadala kwamba thamani katika equation (2) na kutatua kwa\(y\). Kisha, nyuma-mbadala maadili kwa\(z\) na\(y\) katika equation (1) na kutatua kwa\(x\).

\[\begin{align} 5z &= 35,000 \nonumber \\[4pt] z &= 7,000 \nonumber \\[4pt] \nonumber \\[4pt] y+4(7,000) &= 31,000 \nonumber \\[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber\]

John imewekeza\($2,000\) katika mfuko wa fedha soko,\($3,000\) katika vifungo manispaa, na\($7,000\) katika fedha za pande zote.

Zoezi\(\PageIndex{1}\)

Tatua mfumo wa equations katika vigezo vitatu.

\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]

Jibu

\((1,−1,1)\)

Kutambua Mifumo isiyoendana ya milinganyo yenye Vigezo vitatu

Kama vile na mifumo ya equations katika vigezo mbili, tunaweza kuja hela mfumo haiendani ya equations katika vigezo tatu, ambayo ina maana kwamba hana ufumbuzi kwamba satisfies equations zote tatu. Equations inaweza kuwakilisha ndege tatu sambamba, ndege mbili sambamba na ndege moja intersecting, au ndege tatu kwamba intersect nyingine mbili lakini si katika eneo moja. Mchakato wa kuondoa utasababisha taarifa ya uongo, kama vile\(3=7\) au utata mwingine.

Mfano\(\PageIndex{4}\): Solving an Inconsistent System of Three Equations in Three Variables

Tatua mfumo wafuatayo.

\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+13z &=8 \label{4.3} \end{align} \nonumber\]

Suluhisho

Kuangalia coefficients ya\(x\), tunaweza kuona kwamba tunaweza kuondoa\(x\) kwa kuongeza Equation\ ref {4.1} kwa Equation\ ref {4.2}.

\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]

Kisha, tunazidisha equation (1)\(−5\) na na kuongeza kwa equation (3).

\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{multiplied by }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \end{align} \nonumber\]

Kisha, sisi kuzidisha equation (4) na 2 na kuongeza kwa equation (5).

\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{multiplied by }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]

Equation ya mwisho\(0=2\) ni utata, kwa hiyo tunahitimisha kwamba mfumo wa equations haukubaliani na, kwa hiyo, hauna suluhisho.

Uchambuzi

Katika mfumo huu, kila ndege inakabiliana na wengine wawili, lakini si mahali pale. Kwa hiyo, mfumo haukubaliki.

Zoezi\(\PageIndex{2}\)

Tatua mfumo wa equations tatu katika vigezo vitatu.

\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{align} \nonumber\]

Jibu

Hakuna ufumbuzi.

Kuelezea Suluhisho la Mfumo wa Ulinganisho wa Tegemezi Ukiwa na Vigezo vitatu

Tunajua kutokana na kufanya kazi na mifumo ya equations katika vigezo viwili kwamba mfumo wa tegemezi wa equations una idadi isiyo na kipimo ya ufumbuzi. Vile vile ni kweli kwa mifumo ya tegemezi ya equations katika vigezo vitatu. Idadi isiyo na kipimo ya ufumbuzi inaweza kusababisha hali kadhaa. Ndege tatu zinaweza kuwa sawa, ili ufumbuzi wa equation moja itakuwa suluhisho kwa equations nyingine mbili. Equations zote tatu inaweza kuwa tofauti lakini wao intersect juu ya mstari, ambayo ina ufumbuzi usio na mwisho. Au mbili ya equations inaweza kuwa sawa na intersect ya tatu kwenye mstari.

Mfano\(\PageIndex{5}\): Finding the Solution to a Dependent System of Equations

Pata suluhisho la mfumo uliotolewa wa milinganyo mitatu katika vigezo vitatu.

\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y+z &= 0 &(3) \nonumber \end{align} \nonumber\]

Suluhisho

Kwanza, tunaweza kuzidisha equation (1)\(−2\) na na kuongeza kwa equation (2).

\[\begin{align} −4x−2y+6z =0 & (1) \;\;\;\;\; \text{multiplied by }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\]

Hatuna haja ya kuendelea zaidi. Matokeo tunayopata ni utambulisho\(0=0\), ambayo inatuambia kwamba mfumo huu una idadi isiyo na kipimo ya ufumbuzi. Kuna njia nyingine za kuanza kutatua mfumo huu, kama vile kuzidisha equation (3) na\(−2\), na kuongeza kwa equation (1). Sisi kisha kufanya hatua sawa na hapo juu na kupata matokeo sawa,\(0=0\).

Wakati mfumo unategemea, tunaweza kupata maneno ya jumla ya ufumbuzi. Kuongeza equations (1) na (3), tuna

\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align} \nonumber\]

Sisi kisha kutatua equation kusababisha kwa\(z\).

\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]

Sisi nyuma-mbadala kujieleza kwa\(z\) moja ya milinganyo na kutatua kwa\(y\).

\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]

Hivyo suluhisho la jumla ni\(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\). Katika suluhisho hili,\(x\) inaweza kuwa nambari yoyote halisi. Maadili ya\(y\) na\(z\) yanategemea thamani iliyochaguliwa\(x\).

Uchambuzi

Kama inavyoonekana katika Kielelezo\(\PageIndex{5}\), mbili ya ndege ni sawa na wao intersect ndege ya tatu kwenye mstari. Seti ya suluhisho haipatikani, kama pointi zote kwenye mstari wa makutano zitakidhi equations zote tatu.

Kielelezo\(\PageIndex{5}\)

Q & A: Je, ufumbuzi wa generic kwa mfumo tegemezi daima lazima kuandikwa katika suala la\(x\)?

Hapana, unaweza kuandika suluhisho la generic kwa suala la vigezo yoyote, lakini ni kawaida kuandika kwa suala la\(x\) na ikiwa inahitajika\(x\) na\(y\).

Zoezi\(\PageIndex{3}\):

Tatua mfumo wafuatayo.

\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \end{align} \nonumber\]

Jibu

Idadi isiyo na mwisho ya ufumbuzi wa fomu\((x,4x−11,−5x+18)\).

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifumo ya equations katika vigezo vitatu.

• Ex 1: Mfumo wa Equations Tatu na Unknowns Tatu Kutumia Kutumia Kuondoa
• Ex 2: Mfumo wa Equations Tatu na Unknowns Tatu Kutumia Kutumia Kuondoa

Key Concepts

• A solution set is an ordered triple {(x,y,z)} that represents the intersection of three planes in space. See Example \(\PageIndex{1}\).
• A system of three equations in three variables can be solved by using a series of steps that forces a variable to be eliminated. The steps include interchanging the order of equations, multiplying both sides of an equation by a nonzero constant, and adding a nonzero multiple of one equation to another equation. See Example \(\PageIndex{2}\).
• Systems of three equations in three variables are useful for solving many different types of real-world problems. See Example \(\PageIndex{3}\).
• A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction. See Example \(\PageIndex{4}\).
• Systems of equations in three variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location.
• A system of equations in three variables is dependent if it has an infinite number of solutions. After performing elimination operations, the result is an identity. See Example \(\PageIndex{5}\).
• Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or two identical planes that intersect the third on a line.

Contributors

• Template:ContribOpenStaxPreCalc