3.6: Kazi kamili ya Thamani
- Page ID
- 178419
Malengo ya kujifunza
- Graph thamani kamili kazi.
- Kutatua kabisa thamani equation.
Hadi miaka ya 1920, ile inayoitwa nebulae ya ond iliaminika kuwa mawingu ya vumbi na gesi katika galaxi yetu wenyewe, baadhi ya makumi ya maelfu ya miaka ya nuru mbali. Kisha, mwanaastronomia Edwin Hubble alithibitisha kwamba vitu hivi ni galaxi kwa haki yao wenyewe, kwa umbali wa mamilioni ya miaka ya mwanga. Leo, wanaastronomia wanaweza kuchunguza galaxi ambazo ni mabilioni ya miaka nuru mbali. Umbali katika ulimwengu unaweza kupimwa kwa pande zote. Kwa hivyo, ni muhimu kuzingatia umbali kama kazi ya thamani kamili. Katika sehemu hii, tutachunguza kazi za thamani kamili.

Kuelewa Thamani kamili
Kumbuka kwamba katika fomu yake ya msingi\(f(x)=|x|\), kazi ya thamani kamili, ni moja ya kazi zetu za toolkit. Kazi ya thamani kamili ni kawaida hufikiriwa kama kutoa umbali nambari inatoka sifuri kwenye mstari wa nambari. Algebraically, kwa chochote thamani ya pembejeo ni, pato ni thamani bila kujali ishara.
Kazi ya Thamani kamili
Kazi ya thamani kamili inaweza kuelezwa kama kazi ya kipande
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Mfano\(\PageIndex{1}\): Determine a Number within a Prescribed Distance
Eleza maadili yote\(x\) ndani au ikiwa ni pamoja na umbali wa 4 kutoka namba 5.
Suluhisho
Tunataka umbali kati\(x\) na 5 kuwa chini ya au sawa na 4. Tunaweza kuteka mstari wa nambari, kama vile moja, ili kuwakilisha hali ya kuridhika.

Umbali kutoka\(x\) hadi 5 unaweza kuwakilishwa kwa kutumia thamani kamili kama\(|x−5|\). Tunataka maadili ya\(x\) kwamba kukidhi hali\(| x−5 |\leq4\).
Uchambuzi
Kumbuka kwamba
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
Hivyo\(|x−5|\leq4\) ni sawa na\(1{\leq}x\leq9\).
Hata hivyo, wanahisabati kwa ujumla wanapendelea nukuu ya thamani kamili.
Zoezi\(\PageIndex{1}\)
Eleza maadili yote\(x\) ndani ya umbali wa 3 kutoka namba 2.
- Jibu
-
\(|x−2|\leq3\)
Mfano\(\PageIndex{2}\): Resistance of a Resistor
Sehemu za umeme, kama vile resistors na capacitors, huja na maadili maalum ya vigezo vyao vya uendeshaji: upinzani, capacitance, nk Hata hivyo, kutokana na usahihi katika viwanda, maadili halisi ya vigezo hivi hutofautiana kwa kiasi fulani kutoka kipande hadi kipande, hata wakati wanatakiwa kuwa sawa. Bora ambayo wazalishaji wanaweza kufanya ni kujaribu kuhakikisha kwamba tofauti zitabaki ndani ya aina maalum, mara nyingi ± 1%, ± 5%, au ± 10%.
Tuseme tuna kupinga lilipimwa saa 680 ohms, ± 5%. Tumia kazi ya thamani kamili ili kuelezea maadili mbalimbali ya uwezekano wa upinzani halisi.
Suluhisho
5% ya 680 ohms ni 34 ohms. Thamani kamili ya tofauti kati ya upinzani halisi na wa majina haipaswi kuzidi tofauti iliyoelezwa, kwa hiyo, na upinzani\(R\) katika ohms,
\[|R−680|\leq34 \nonumber\]
Zoezi\(\PageIndex{2}\)
Wanafunzi ambao alama ndani ya pointi 20 ya 80 watapita mtihani. Andika hii kama umbali kutoka 80 ukitumia notation ya thamani kamili.
- Jibu
-
Kutumia variable\(p\) kwa kupita,\(| p−80 |\leq20\)
Kuweka Kazi ya Thamani kamili
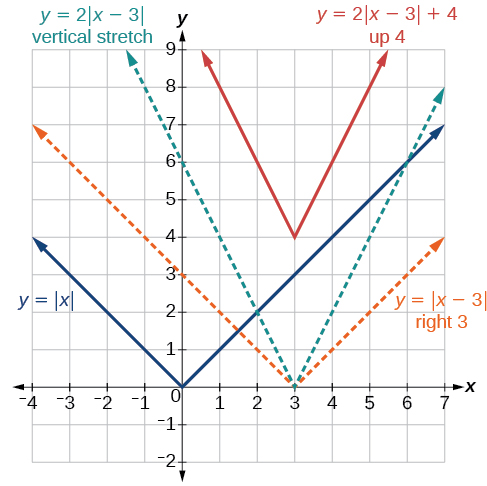
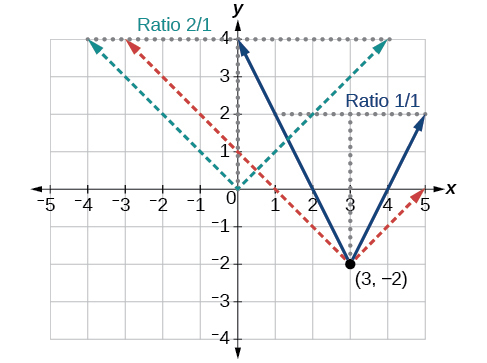
Kipengele muhimu zaidi cha grafu ya thamani kamili ni hatua ya kona ambayo grafu inabadilisha mwelekeo. Hatua hii inavyoonekana katika asili katika Kielelezo\(\PageIndex{3}\).
Kielelezo\(\PageIndex{3}\) inaonyesha grafu ya\(y=2|x–3|+4\). Grafu ya\(y=|x|\) imebadilishwa vitengo 3 vya haki, vilivyowekwa kwa wima kwa sababu ya 2, na kubadilishwa hadi vitengo 4. Hii ina maana kwamba hatua ya kona iko kwenye\((3,4)\) kazi hii iliyobadilishwa.
Mfano\(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
Andika equation kwa ajili ya kazi graphed katika Kielelezo\(\PageIndex{5}\).
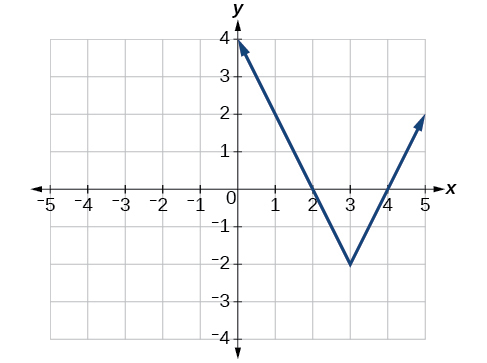
Suluhisho
Kazi ya msingi ya thamani kabisa inabadilisha mwelekeo kwa asili, hivyo grafu hii imebadilishwa kwa vitengo 3 vya haki na chini ya vitengo 2 kutoka kwa kazi ya msingi ya toolkit. Angalia Kielelezo\(\PageIndex{6}\).
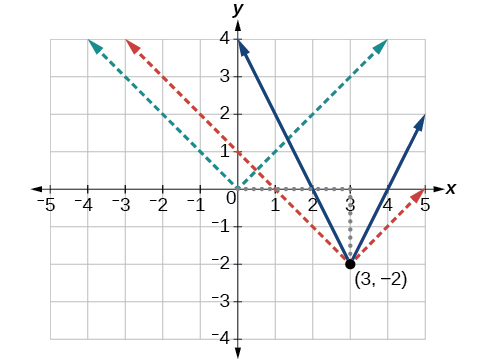
Pia tunaona kwamba grafu inaonekana kwa wima, kwa sababu upana wa grafu ya mwisho kwenye mstari wa usawa si sawa na mara 2 umbali wa wima kutoka kona hadi mstari huu, kama ingekuwa kwa kazi isiyo ya thamani kamili. Badala yake, upana ni sawa na mara 1 umbali wima kama inavyoonekana katika Kielelezo\(\PageIndex{7}\).
Kutokana na habari hii tunaweza kuandika equation
\[\begin{align*} f(x)&=2|x-3|-2, \;\;\;\;\;\; \text{treating the stretch as a vertial stretch, or} \\ f(x)&=|2(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal compression.} \end{align*}\]
Uchambuzi
Kumbuka kuwa equations hizi ni algebraically sawa-kunyoosha kwa kazi ya thamani kamili inaweza kuandikwa kwa kubadilishana kama kunyoosha wima au usawa au compression.
Q & A
Kama hatukuweza kuchunguza kunyoosha ya kazi kutoka grafu, tunaweza algebraically kuamua ni?
- Jibu
-
Ndiyo. Ikiwa hatuwezi kuamua kunyoosha kulingana na upana wa grafu, tunaweza kutatua kwa sababu ya kunyoosha kwa kuweka jozi inayojulikana ya maadili kwa\(x\) na\(f(x)\).
\[f(x)=a|x−3|−2 \nonumber\]
Sasa badala katika hatua\((1, 2)\)
\[\begin{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=2 \end{align*}\]
Zoezi\(\PageIndex{3}\)
Andika equation kwa kazi kamili ya thamani ambayo ni usawa kubadilishwa kushoto vitengo 2, ni wima flipped, na wima kubadilishwa hadi 3 vitengo.
- Jibu
-
\(f(x)=−| x+2 |+3\)
Q & A
Je! Grafu za kazi za thamani kamili daima zinaingiliana na mhimili wima? Mhimili usio na usawa?
- Jibu
-
Ndiyo, daima huingiliana na mhimili wima. Grafu ya kazi ya thamani kamili itaingiliana na mhimili wima wakati pembejeo ni sifuri.
Hapana, sio daima huingiliana na mhimili usio na usawa. Grafu inaweza au haipatikani mhimili usio na usawa, kulingana na jinsi grafu imebadilishwa na kuonekana. Inawezekana kwa kazi kamili ya thamani ya kuingiliana na mhimili usio na usawa kwenye sifuri, moja, au pointi mbili (Kielelezo\(\PageIndex{8}\)).
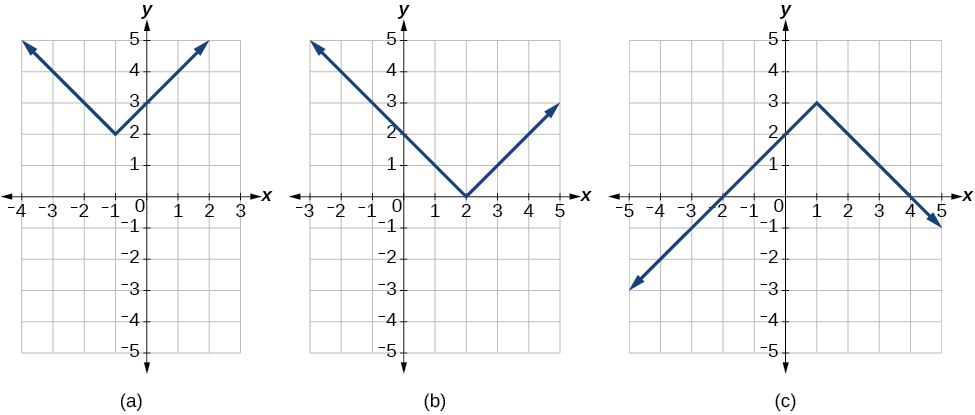
Kielelezo\(\PageIndex{8}\): (a) Kazi ya thamani kamili haina intersect mhimili usawa. (b) Kazi ya thamani kamili inakabiliana na mhimili usio na usawa kwa hatua moja. (c) Kazi ya thamani kamili inakabiliana na mhimili usio na usawa katika pointi mbili.
Kutatua Equation ya Thamani kamili
Sasa kwa kuwa tunaweza graph kabisa thamani kazi, sisi kujifunza jinsi ya kutatua kabisa thamani equation. Ili kutatua equation kama vile\(8=|2x−6|\), tunaona kwamba thamani kamili itakuwa sawa na 8 ikiwa wingi ndani ya thamani kamili ni 8 au -8. Hii inasababisha equations mbili tofauti tunaweza kutatua kwa kujitegemea.
\[2x-6=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & x&=-1 \end{align*}\]
Kujua jinsi ya kutatua matatizo yanayohusisha kazi za thamani kamili ni muhimu. Kwa mfano, tunaweza kuhitaji kutambua namba au pointi kwenye mstari ulio umbali maalum kutoka kwenye hatua ya kumbukumbu iliyotolewa.
Equation ya thamani kamili ni equation ambayo kutofautiana haijulikani inaonekana katika baa thamani kabisa. Kwa mfano,
\[\begin{align*}|x|&=4, \nonumber \\[4pt] |2x−1| &=3, \\[4pt] |5x+2|−4 &=9. \end{align*}\]
Ufumbuzi wa Ulinganisho wa Thamani kamili
Kwa idadi halisi\(A\) na\(B\), equation ya fomu\(|A|=B\), na\(B\geq0\), itakuwa na ufumbuzi wakati\(A=B\) au\(A=−B\). Kama\(B<0\), equation\(|A|=B\) haina ufumbuzi.
Jinsi ya...
Kutokana na formula ya kazi ya thamani kamili, pata uingizaji usio na usawa wa grafu yake.
- Sulua muda wa thamani kamili.
- Matumizi\(|A|=B\) ya kuandika\(A=B\) au\(−A=B\), kuchukua\(B>0\).
- Kutatua kwa\(x\).
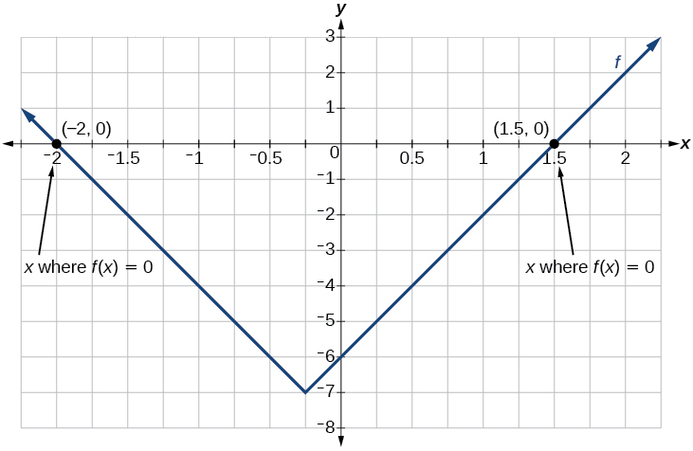
Mfano\(\PageIndex{4}\): Finding the Zeros of an Absolute Value Function
Kwa kazi\(f(x)=|4x+1|−7\), tafuta maadili ya\(x\) vile vile\(f(x)=0\).
Suluhisho
\[\begin{align*} 0&=|4x+1|-7 & & &\text{Substitute 0 for f(x).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Break into two separate equations and solve.} \\ 6&=4x & -8&=4x & \\ x&=\frac{6}{4}=1.5 & x&=\frac{-8}{4}=-2 \end{align*}\]
Matokeo ya kazi 0 wakati\(x=1.5\) au\(x=−2\) (Kielelezo\(\PageIndex{9}\)).
Zoezi\(\PageIndex{4}\)
Kwa kazi\(f(x)=|2x−1|−3\), tafuta maadili ya\(x\) vile vile\(f(x)=0\).
Suluhisho
\(x=−1\)au\(x=2\)
Q & A
Je, tunapaswa kutarajia majibu mawili wakati wa kutatua\(|A|=B\)?
Jibu
Hapana. Tunaweza kupata moja, mbili, au hata hakuna majibu. Kwa mfano, hakuna ufumbuzi wa\(2+|3x−5|=1\).
Jinsi ya...
Kutokana na usawa wa thamani kamili, tatua.
- Sulua muda wa thamani kamili.
- \(|A|=B\)Tumia kuandika\(A=B\) au\(A=−B\).
- Kutatua kwa\(x\).
Mfano\(\PageIndex{5}\): Solving an Absolute Value Equation
Kutatua\(1=4|x−2|+2\).
Suluhisho
Kutenganisha thamani kamili upande mmoja wa equation hutoa zifuatazo.
\[\begin{align*} 1&=4|x-2|+2 \\ -1&=4|x-2| \\ -\frac{1}{4}&=|x-2| \end{align*}\]
Thamani kamili daima inarudi thamani nzuri, hivyo haiwezekani kwa thamani kamili kuwa sawa na thamani hasi. Kwa hatua hii, tunaona kwamba equation hii haina ufumbuzi.
Q & A
Katika Mfano\(\PageIndex{5}\), ikiwa\(f(x)=1\) na\(g(x)=4|x−2|+2\) umewekwa kwenye seti moja ya shaba, ingekuwa grafu zitaingiliana?
Jibu
Hapana. Grafu ya\(f\) na\(g\) bila intersect, kama inavyoonekana katika Kielelezo\(\PageIndex{10}\). Hii inathibitisha, graphically, kwamba equation\(1=4|x−2|+2\) haina ufumbuzi.
Pata ambapo grafu ya kazi\(f(x)=−| x+2 |+3\) inakabiliana na axes za usawa na wima.
\(f(0)=1\), hivyo grafu inakabiliana na mhimili wima\((0,1)\). \(f(x)=0\)wakati\(x=−5\) na\(x=1\) hivyo grafu inakabiliana na mhimili usio na usawa\((−5,0)\) na\((1,0)\).
Kutatua Ukosefu wa Thamani kamili
Ulinganifu wa thamani kamili hauwezi kuhusisha usawa. Badala yake, tunaweza haja ya kutatua equation ndani ya aina mbalimbali ya maadili. Tunataka kutumia usawa kabisa thamani ya kutatua equation vile. Thamani kamili ya usawa ni equation ya fomu
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
au
\[ |A|{\geq}B, \nonumber\]
ambapo kujieleza\(A\) (na labda lakini si kawaida\(B\)) inategemea kutofautiana\(x\). Kutatua usawa kunamaanisha kutafuta seti ya yote\(x\) ambayo yanakidhi usawa. Kawaida kuweka hii itakuwa muda au umoja wa vipindi viwili.
Kuna mbinu mbili za msingi za kutatua usawa wa thamani kabisa: graphical na algebraic. Faida ya mbinu ya kielelezo ni tunaweza kusoma suluhisho kwa kutafsiri grafu za kazi mbili. Faida ya mbinu ya algebraic ni hutoa ufumbuzi ambao unaweza kuwa vigumu kusoma kutoka kwenye grafu.
Kwa mfano, tunajua kwamba idadi yote ndani ya vitengo 200 ya 0 inaweza kuwa walionyesha kama
\[|x|<200 \nonumber\]
au
\[ −200<x<200 \nonumber\]
Tuseme tunataka kujua faida zote iwezekanavyo kwenye uwekezaji kama tunaweza kupata kiasi fulani cha fedha ndani ya $200 ya $600. Tunaweza kutatua algebraically kwa seti ya maadili\(x\) kama umbali kati\(x\) na 600 ni chini ya 200. Sisi kuwakilisha umbali kati\(x\) na 600 kama\(|x−600|\).
\[|x−600|<200\]
au
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
Hii ina maana anarudi yetu itakuwa kati ya $400 na $800.
Wakati mwingine kabisa thamani kukosekana kwa usawa tatizo itawasilishwa kwetu katika suala la kubadilishwa na/au aliweka au USITUMIE kabisa thamani kazi, ambapo ni lazima kuamua ambayo maadili ya pembejeo kazi ya pato itakuwa hasi au chanya.
Jinsi ya...
Kutokana na usawa wa thamani kamili ya fomu\(|x−A|{\leq}B\) kwa idadi halisi\(a\) na\(b\) wapi\(b\) ni chanya, tatua usawa wa thamani kamili kwa algebraically.
- Kupata pointi mipaka na kutatua\(|x−A|=B\).
- Vipindi vya mtihani vilivyoundwa na pointi za mipaka ili kuamua wapi\(|x−A|{\leq}B\).
- Andika muda au muungano wa vipindi vinavyolidhisha usawa katika muda, usawa, au ubaguzi wa wajenzi wa kuweka.
Mfano\(\PageIndex{6}\): Solving an Absolute Value Inequality
Kutatua\(|x −5|{\leq}4\).
Suluhisho
Kwa njia zote mbili, tutahitaji kujua kwanza ambapo usawa unaofanana ni wa kweli. Katika kesi hii sisi kwanza tutapata wapi\(|x−5|=4\). Sisi kufanya hivyo kwa sababu thamani kamili ni kazi na mapumziko hakuna, hivyo njia pekee ya maadili ya kazi unaweza kubadili kutoka kuwa chini ya 4 kwa kuwa zaidi ya 4 ni kwa kupitia ambapo maadili sawa 4. Kutatua\(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
Baada ya kuamua kwamba thamani kamili ni sawa na 4\(x=1\) na\(x=9\), tunajua grafu inaweza kubadilika tu kutokana na kuwa chini ya 4 hadi zaidi ya 4 kwa maadili haya. Hii inagawanya mstari wa nambari hadi vipindi vitatu:
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
Kuamua wakati kazi ni chini ya 4, tunaweza kuchagua thamani katika kila kipindi na kuona kama pato ni chini ya au zaidi ya 4, kama inavyoonekana katika Jedwali\(\PageIndex{1}\).
| Mtihani wa muda\(x\) | \(f(x)\) | \(<4\)au\(>4\) | |
|---|---|---|---|
| \ (x\)” style="wima align:katikati; ">\(x<1\) | \ (f (x)\)” style="wima align:katikati; "> 0 | \ (<4\) au\(>4\) "style="wima align:middle;" >\(|0-5|=5\) | Kubwa kuliko |
| \ (x\)” style="wima align:katikati; ">\(1<x<9\) | \ (f (x)\)” style="wima align:katikati; "> 6 | \ (<4\) au\(>4\) "style="wima align:middle;" >\(|6-5|=1\) | Chini ya |
| \ (x\)” style="wima align:katikati; ">\(x>9\) | \ (f (x)\)” style="wima align:katikati; "> 11 | \ (<4\) au\(>4\) "style="wima align:middle;" >\(|11-5|=6\) | Kubwa kuliko |
Kwa sababu\(1{\leq}x{\leq}9\) ni muda pekee ambao pato katika thamani ya mtihani ni chini ya 4, tunaweza kuhitimisha kuwa suluhisho\(|x−5|{\leq}4\) ni\(1{\leq}x{\leq}9\), au\([1,9]\).
Ili kutumia grafu, tunaweza kuchora kazi\(f(x)=|x−5|\). Ili kutusaidia kuona ambapo matokeo ni 4, mstari pia\(g(x)=4\) inaweza sketched kama katika Kielelezo\(\PageIndex{11}\).
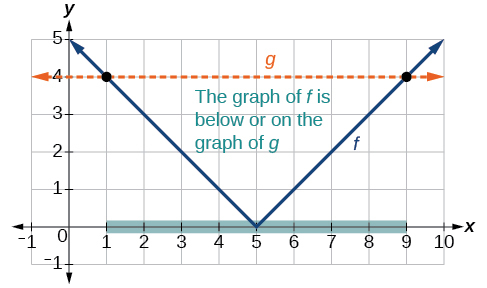
Tunaweza kuona zifuatazo:
- Maadili ya pato ya thamani kamili ni sawa na 4 saa\(x=1\) na\(x=9\).
- Grafu ya\(f\) iko chini ya grafu ya\(g\) juu\(1<x<9\). Hii ina maana maadili pato ya\(f(x)\) ni chini ya maadili pato la\(g(x)\).
- Thamani kamili ni chini ya au sawa na 4 kati ya pointi hizi mbili, wakati\(1{\leq}x\leq9\). Katika notation ya muda, hii itakuwa muda\([1,9]\).
Uchambuzi
Kwa kukosekana kwa usawa wa thamani kabisa,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
\(<\)au\(>\) ishara inaweza kubadilishwa na\(\leq\) au\(\geq\).
Kwa hiyo, kwa mfano huu, tunaweza kutumia njia hii mbadala.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]
Zoezi\(\PageIndex{5}\)
Kutatua\(|x+2| \leq 6\).
- Jibu
-
\(-8 \leq x \leq 4\)
Jinsi ya...
Kutokana na kazi kamili ya thamani, tatua kwa seti ya pembejeo ambapo pato ni chanya (au hasi).
- Weka kazi sawa na sifuri, na usuluhishe kwa pointi za mipaka ya kuweka suluhisho.
- Tumia pointi za mtihani au grafu ili uone wapi pato la kazi ni chanya au hasi.
Mfano\(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
Kutokana na kazi\(f(x)=−\frac{1}{2}|4x−5|+3\), tambua\(x\) maadili ambayo maadili ya kazi ni hasi.
Suluhisho
Tunajaribu kuamua wapi\(f(x)<0\), ni wakati gani\(−\frac{1}{2}|4x−5|+3<0\). Tunaanza kwa kutenganisha thamani kamili.
\[ \begin{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−5|&>6\end{align*}\]
Halafu tunatatua kwa usawa\(|4x−5|=6\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=6 \end{align*}\]
au
\[\begin{align*} 4x&=-1 \\ x&=\frac{11}{4} & x&=-\frac{1}{4} \end{align*}\]
Sasa, tunaweza kuchunguza grafu ya\(f\) kuchunguza ambapo pato ni hasi. Tutaona ambapo matawi ni chini ya\(x\) -axis. Kumbuka kwamba sio muhimu hata kile ambacho grafu inaonekana kama, kwa muda mrefu kama tunajua kwamba inavuka mhimili usio na usawa\(x=−\frac{1}{4}\)\(x=\frac{11}{4}\) na kwamba grafu imeonekana kwa wima. Angalia Kielelezo\(\PageIndex{12}\).
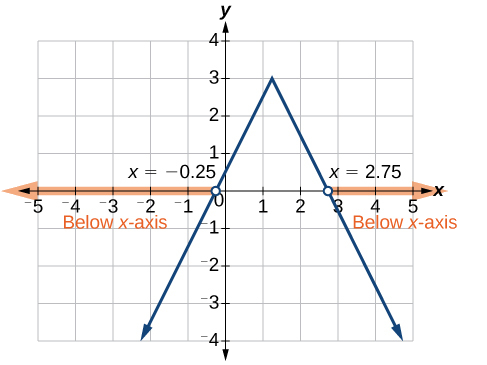
Tunaona kwamba grafu ya kazi iko chini ya\(x\) -axis kushoto\(x=−\frac{1}{4}\) na kulia ya\(x=\frac{11}{4}\). Hii inamaanisha maadili ya kazi ni hasi upande wa kushoto wa kuingilia kwanza usawa\(x=−\frac{1}{4}\), na hasi kwa haki ya kuingilia pili saa\(x=\frac{11}{4} \). Hii inatupa suluhisho la kukosekana kwa usawa.
\[x<−\frac{1}{4} \text{ or } x>1\frac{1}{4} \nonumber\]
Katika nukuu ya muda, hii itakuwa\(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Zoezi\(\PageIndex{6}\)
Kutatua\(−2|k−4|\leq−6\).
- Jibu
-
\(k\leq1\)au\(k\geq7\); katika nukuu ya muda, hii itakuwa\(\left(−\infty,1\right]\cup\left[7,\infty\right)\)
Dhana muhimu
- Kazi ya thamani kamili hutumiwa kupima umbali kati ya pointi.
- Matatizo yaliyotumika, kama vile viwango vya maadili iwezekanavyo, yanaweza pia kutatuliwa kwa kutumia kazi ya thamani kamili.
- Grafu ya kazi ya thamani kamili inafanana na barua V. ina hatua ya kona ambayo grafu inabadilisha mwelekeo.
- Katika usawa wa thamani kabisa, kutofautiana haijulikani ni pembejeo ya kazi ya thamani kamili.
- Kama thamani kamili ya kujieleza ni kuweka sawa na idadi chanya, kutarajia ufumbuzi mbili kwa kutofautiana haijulikani.
- Equation ya thamani kamili inaweza kuwa na suluhisho moja, ufumbuzi mbili, au hakuna ufumbuzi.
- Ukosefu wa usawa wa thamani kabisa ni sawa na equation ya thamani kamili lakini inachukua fomu | A |B<B, | A |≤B, | A |>, au | A |≥ B.Inaweza kutatuliwa kwa kuamua mipaka ya kuweka suluhisho na kisha kupima ni makundi gani yaliyo katika seti.
- Usawa wa thamani kamili pia unaweza kutatuliwa graphically.
faharasa
thamani kamili
equation equation ya fomu\(|A|=B\), kwa\(B\geq0\); itakuwa na ufumbuzi wakati\(A=B\) au\(A=−B\)
thamani kamili usawa
uhusiano katika fomu\(|A|<B\),\(|A|{\leq}B\),\(|A|>B\), au\(|A|{\geq}B\)


