3.2: Domain na Range
- Page ID
- 178376
Malengo ya kujifunza
- Kupata uwanja wa kazi inavyoelezwa na equation.
- Graph kazi piecewise-defined.
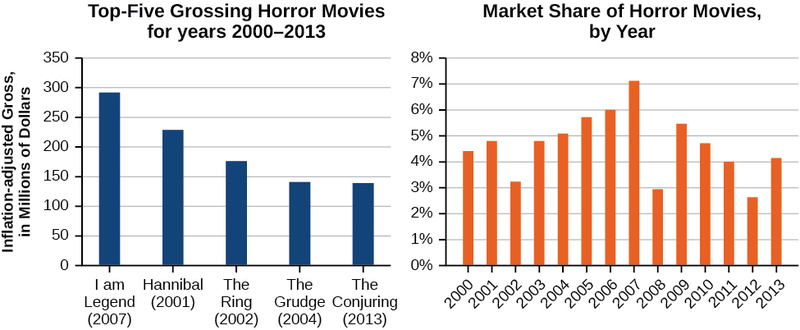
Ikiwa uko katika hali ya movie ya kutisha, unaweza kutaka kuangalia moja ya sinema tano maarufu zaidi za kutisha za wakati wote—Mimi ni Legend, Hannibal, The Ring, The Grudge, na The Conjuring. Kielelezo\(\PageIndex{1}\) inaonyesha kiasi, katika dola, kila moja ya sinema hizo grossed wakati wao walikuwa iliyotolewa pamoja na mauzo ya tiketi kwa ajili ya sinema horror kwa ujumla kwa mwaka. Kumbuka kwamba tunaweza kutumia data kujenga kazi ya kiasi kila movie chuma au jumla ya mauzo ya tiketi kwa sinema zote hofu kwa mwaka. Katika kujenga kazi mbalimbali kwa kutumia data, tunaweza kutambua vigezo tofauti vya kujitegemea na vya tegemezi, na tunaweza kuchambua data na kazi za kuamua uwanja na upeo. Katika sehemu hii, tutachunguza mbinu za kuamua uwanja na kazi mbalimbali kama hizi.
Kutafuta Domain ya Kazi Inafafanuliwa na Equation
Katika Kazi na Uthibitishaji wa Kazi, tulianzishwa kwa dhana za kikoa na upeo. Katika sehemu hii, tutafanya mazoezi ya kuamua vikoa na safu za kazi maalum. Kumbuka kwamba, katika kuamua vikoa na safu, tunahitaji kuzingatia kile kinachowezekana kimwili au kinachowezekana katika mifano halisi ya ulimwengu, kama vile mauzo ya tiketi na mwaka katika mfano wa filamu ya kutisha hapo juu. Sisi pia haja ya kufikiria nini ni hesabu inaruhusiwa. Kwa mfano, hatuwezi kuingiza thamani yoyote ya pembejeo ambayo inatuongoza kuchukua hata mizizi ya nambari hasi ikiwa kikoa na upeo hujumuisha namba halisi. Au katika kazi iliyoonyeshwa kama formula, hatuwezi kuingiza thamani yoyote ya pembejeo katika uwanja ambao utatuongoza kugawanya na 0.
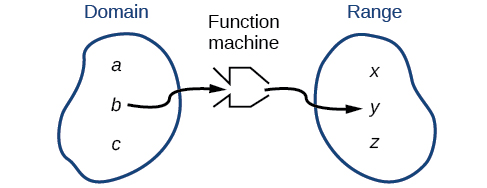
Tunaweza kutazama kikoa kama “eneo la kushikilia” ambalo lina “malighafi” kwa “mashine ya kazi” na aina kama “eneo lingine la kushikilia” kwa bidhaa za mashine (Kielelezo\(\PageIndex{2}\)).
Tunaweza kuandika kikoa na upeo katika notation ya muda, ambayo inatumia maadili ndani ya mabano kuelezea seti ya namba. Katika nukuu ya muda, tunatumia bracket ya mraba [wakati seti inajumuisha mwisho na mabano (kuonyesha kwamba mwisho wa mwisho haujumuishwa au muda hauhusiani. Kwa mfano, ikiwa mtu ana dola 100 ya kutumia, angehitaji kuelezea muda ambao ni zaidi ya 0 na chini ya au sawa na 100 na kuandika\(\left(0, 100\right]\). Tutajadili maelezo ya muda kwa undani zaidi baadaye.
Hebu tuelekeze mawazo yetu kutafuta uwanja wa kazi ambao equation hutolewa. Mara nyingi, kutafuta uwanja wa kazi hizo kunahusisha kukumbuka aina tatu tofauti. Kwanza, kama kazi haina denominator au hata mizizi, fikiria kama uwanja inaweza kuwa namba zote halisi. Pili, kama kuna denominator katika equation kazi ya, kuondoa maadili katika uwanja kwamba nguvu denominator kuwa sifuri. Tatu, ikiwa kuna mizizi hata, fikiria ukiondoa maadili ambayo ingeweza kufanya radicna hasi.
Kabla ya kuanza, hebu tupate mapitio ya uhalali wa muda:
- Muda mdogo zaidi kutoka kwa muda umeandikwa kwanza.
- Neno kubwa zaidi katika kipindi hicho limeandikwa pili, kufuatia comma.
- Mabano\()\),\((\) au, hutumiwa kuashiria kwamba mwisho haujajumuishwa, inayoitwa kipekee.
- Mabano\(]\),\([\) au, hutumiwa kuonyesha kwamba mwisho wa mwisho umejumuishwa, unaoitwa umoja.
Angalia Kielelezo\(\PageIndex{3}\) kwa muhtasari wa nukuu ya muda.
Mfano\(\PageIndex{1}\): Finding the Domain of a Function as a Set of Ordered Pairs
Pata uwanja wa kazi ifuatayo:\(\{(2, 10),(3, 10),(4, 20),(5, 30),(6, 40)\}\).
Suluhisho
Kwanza kutambua maadili ya pembejeo. Thamani ya pembejeo ni kuratibu ya kwanza katika jozi iliyoamriwa. Hakuna vikwazo, kama jozi zilizoamriwa zimeorodheshwa tu. Kikoa ni seti ya kuratibu za kwanza za jozi zilizoamriwa.
\[\{2,3,4,5,6\} \nonumber\]
Zoezi\(\PageIndex{1}\)
Pata uwanja wa kazi:
\[\{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)\} \nonumber\]
- Jibu
-
\(\{−5, 0, 5, 10, 15\}\)
Jinsi ya: Kutokana na kazi iliyoandikwa katika fomu equation, kupata domain.
- Tambua maadili ya pembejeo.
- Tambua vikwazo vyovyote kwenye pembejeo na uondoe maadili hayo kutoka kwenye kikoa.
- Andika kikoa katika fomu ya muda, ikiwa inawezekana.
Mfano\(\PageIndex{2}\): Finding the Domain of a Function
Pata uwanja wa kazi\(f(x)=x^2−1\).
Suluhisho
Thamani ya pembejeo, iliyoonyeshwa na x ya kutofautiana katika equation, ni mraba na kisha matokeo hupungua kwa moja. Nambari yoyote halisi inaweza kuwa mraba na kisha kupunguzwa na moja, kwa hiyo hakuna vikwazo kwenye uwanja wa kazi hii. Kikoa ni seti ya namba halisi.
Katika fomu ya muda, uwanja wa f ni\((−\infty,\infty)\).
Zoezi\(\PageIndex{2}\)
Pata uwanja wa kazi:
\[f(x)=5−x+x^3 \nonumber\]
- Jibu
-
\((−\infty,\infty)\)
Howto: Kutokana na kazi iliyoandikwa katika fomu ya equation inayojumuisha sehemu, tafuta kikoa
- Tambua maadili ya pembejeo.
- Tambua vikwazo vyovyote kwenye pembejeo. Ikiwa kuna denominator katika fomu ya kazi, weka denominator sawa na sifuri na kutatua kwa x. Ikiwa formula ya kazi ina mizizi hata, weka radicana kubwa kuliko au sawa na 0, na kisha kutatua.
- Andika kikoa katika fomu ya muda, uhakikishe kuwatenga maadili yoyote yaliyozuiliwa kutoka kwenye kikoa.
Mfano\(\PageIndex{3}\): Finding the Domain of a Function Involving a Denominator
Pata uwanja wa kazi\(f(x)=\dfrac{x+1}{2−x}\).
Suluhisho
Wakati kuna denominator, tunataka kuingiza maadili tu ya pembejeo ambayo hayalazimisha denominator kuwa sifuri. Kwa hiyo, tutaweka denominator sawa na 0 na kutatua kwa x.
\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]
Sasa, tutaondoa 2 kutoka kwenye kikoa. majibu ni namba zote halisi ambapo\(x<2\) au\(x>2\). Tunaweza kutumia ishara inayojulikana kama muungano\(\cup\),, kuchanganya seti mbili. Katika maelezo ya muda, tunaandika suluhisho:\((−\infty,2)∪(2,\infty)\).
![[Grafu ya mstari wa f (x).]](https://math.libretexts.org/@api/deki/files/893/CNX_Precalc_Figure_01_02_028n.jpg)
Katika fomu ya muda, uwanja wa f ni\((−\infty,2)\cup(2,\infty)\).
Zoezi\(\PageIndex{3}\)
Pata uwanja wa kazi:
\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]
- Jibu
-
\[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]
Jinsi ya: Kutokana na kazi iliyoandikwa katika fomu equation ikiwa ni pamoja na hata mizizi, kupata uwanja.
- Tambua maadili ya pembejeo.
- Kwa kuwa kuna hata mizizi, ukiondoa namba yoyote halisi ambayo husababisha idadi hasi katika radicand. Weka radicna kubwa kuliko au sawa na sifuri na kutatua kwa x.
- Suluhisho (s) ni uwanja wa kazi. Ikiwezekana, weka jibu kwa fomu ya muda.
Mfano\(\PageIndex{4}\): Finding the Domain of a Function with an Even Root
Pata uwanja wa kazi:
\[f(x)=\sqrt{7-x} \nonumber .\]
Suluhisho
Wakati kuna mizizi hata katika formula, tunaondoa namba yoyote halisi ambayo husababisha idadi hasi katika radicand.
Weka radicna kubwa kuliko au sawa na sifuri na kutatua kwa x.
\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]
Sasa, tutaondoa nambari yoyote kubwa kuliko 7 kutoka kwenye kikoa. Majibu yote ni namba halisi chini ya au sawa na 7, au\(\left(−\infty,7\right]\).
Zoezi\(\PageIndex{4}\)
Pata uwanja wa kazi
\[f(x)=\sqrt{5+2x}. \nonumber\]
- Jibu
-
\[\left[−2.5,\infty\right) \nonumber\]
Q & A: Je, kuna kazi ambazo uwanja na upeo hauingiliani kabisa?
Ndiyo. Kwa mfano, kazi\(f(x)=-\dfrac{1}{\sqrt{x}}\) ina seti ya nambari zote halisi nzuri kama uwanja wake lakini seti ya namba zote hasi halisi kama aina yake. Kama mfano uliokithiri zaidi, pembejeo za kazi na matokeo zinaweza kuwa makundi tofauti kabisa (kwa mfano, majina ya siku za wiki kama pembejeo na namba kama matokeo, kama kwenye chati ya mahudhurio), katika hali hiyo uwanja na upeo hauna mambo sawa.
Kutumia Notations kutaja Domain na Range
Katika mifano ya awali, tulitumia kutofautiana na orodha kuelezea uwanja wa kazi. Tunaweza pia kutumia usawa, au kauli nyingine ambayo inaweza kufafanua seti ya maadili au data, kuelezea tabia ya kutofautiana katika kuweka wajenzi nukuu. Kwa mfano,\(\{x|10≤x<30\}\) inaelezea tabia ya x katika nukuu ya kuweka-wajenzi. Braces\(\{\}\) ni kusoma kama “seti ya,” na bar wima\(|\) ni kusoma kama “kama kwamba,” hivyo tunaweza kusoma\( \{x|10≤x<30\}\) kama “seti ya x-maadili kama kwamba 10 ni chini ya au sawa na x, na x ni chini ya 30.”
Kielelezo\(\PageIndex{4}\) kulinganisha usawa notation, kuweka-wajenzi nukuu, na muda nukuu.
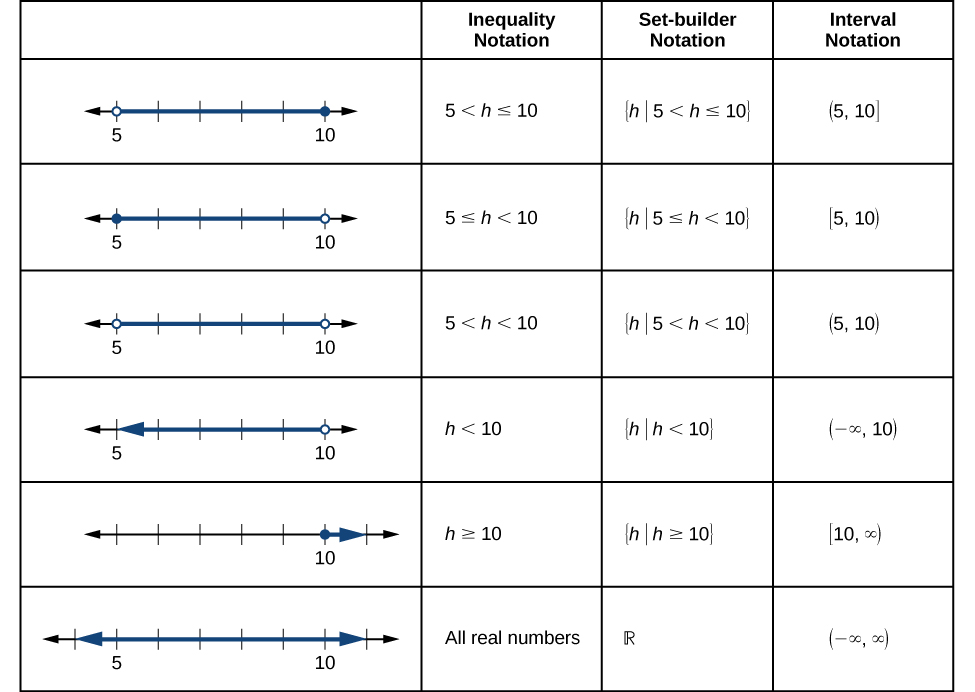
Ili kuchanganya vipindi viwili kwa kutumia notation ya usawa au notation ya kuweka-wajenzi, tunatumia neno “au.” Kama tulivyoona katika mifano ya awali, tunatumia alama ya muungano\(\cup\), kuchanganya vipindi viwili visivyounganishwa. Kwa mfano, umoja wa seti\(\{2,3,5\}\) na\(\{4,6\}\) ni kuweka\(\{2,3,4,5,6\}\). Ni seti ya vipengele vyote ambavyo ni vya moja au nyingine (au vyote viwili) vya seti mbili za awali. Kwa seti zilizo na idadi ya mwisho ya vipengele kama hizi, vipengele havihitaji kuorodheshwa katika utaratibu wa kupanda wa thamani ya namba. Ikiwa seti mbili za awali zina vipengele vingine, vipengele hivi vinapaswa kuorodheshwa mara moja tu katika kuweka muungano. Kwa seti ya idadi halisi juu ya vipindi, mfano mwingine wa muungano ni
\[\{x| |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]
Uthibitishaji wa Wajenzi wa Kuweka na Uthibitishaji wa Muda
Uthibitishaji wa wajenzi wa kuweka ni njia ya kutaja seti ya vipengele vinavyokidhi hali fulani. Inachukua fomu\(\{x|\text{ statement about x}\}\) ambayo inasomwa kama, “seti ya x wote kama kwamba taarifa kuhusu x ni kweli.” Kwa mfano,
\[\{x|4<x≤12\} \nonumber\]
Muda nukuu ni njia ya kuelezea seti zinazojumuisha namba zote halisi kati ya kikomo cha chini ambacho kinaweza au kisichojumuishwa na kikomo cha juu ambacho kinaweza au kisichoingizwa. Maadili ya mwisho yameorodheshwa kati ya mabano au mabano. Bracket ya mraba inaonyesha kuingizwa katika kuweka, na mabano yanaonyesha kutengwa kutoka kwenye seti. Kwa mfano,
\[\left(4,12\right] \nonumber\]
![]() Kutokana na grafu ya mstari, kuelezea seti ya maadili kwa kutumia notation ya muda.
Kutokana na grafu ya mstari, kuelezea seti ya maadili kwa kutumia notation ya muda.
- Tambua vipindi vinavyoingizwa katika kuweka kwa kuamua wapi mstari nzito unashughulikia mstari halisi.
- Katika mwisho wa kushoto wa kila kipindi, tumia [na kila thamani ya mwisho ili kuingizwa katika seti (dot imara) au (kwa kila thamani ya mwisho iliyotengwa (wazi dot).
- Wakati wa mwisho wa kila kipindi, tumia] na kila thamani ya mwisho ili kuingizwa katika seti (dot iliyojaa) au) kwa kila thamani ya mwisho iliyotengwa (wazi dot).
- Tumia ishara ya\(\cup\) muungano kuchanganya vipindi vyote katika seti moja.
Mfano\(\PageIndex{5}\): Describing Sets on the Real-Number Line
Eleza vipindi vya maadili inavyoonekana katika Kielelezo\(\PageIndex{5}\) kwa kutumia usawa nukuu, kuweka-wajenzi nukuu, na nukuu ya muda.
Suluhisho
Kuelezea maadili,\(x\), pamoja na katika vipindi inavyoonekana, tunaweza kusema, “\(x\)ni idadi halisi kubwa kuliko au sawa na 1 na chini ya au sawa na 3, au idadi halisi zaidi ya 5.”
Ukosefu wa usawa
\[1≤x≤3 \text{ or }x>5 \nonumber\]
Kuweka-wajenzi nukuu
\[\{x|1≤x≤3 \text{ or } x>5\}\nonumber\]
Muda nukuu
\[[1,3]\cup(5,\infty)\nonumber\]
Kumbuka kwamba, wakati wa kuandika au kusoma maelezo ya muda, kutumia bracket ya mraba inamaanisha mipaka imejumuishwa katika kuweka. Kutumia mabano inamaanisha mipaka haijaingizwa katika kuweka.
Zoezi\(\PageIndex{5}\)
Kutokana Kielelezo\(\PageIndex{6}\), taja kuweka graphid katika
- maneno
- kuweka-wajenzi nukuu
- nukuu ya muda
![[Grafu ya mstari wa -2<=x, -1<=x<3.]](https://math.libretexts.org/@api/deki/files/877/CNX_Precalc_Figure_01_02_005.jpg)
- Jibu
-
Maadili ambayo ni chini ya au sawa na —2, au maadili ambayo ni makubwa kuliko au sawa na -1 na chini ya 3;
- Jibu b
-
\(\{x|x≤−2 or −1≤x<3\}\)
- Jibu c
-
\(\left(−∞,−2\right]\cup\left[−1,3\right)\)
Kupata Domain na Range kutoka Grafu
Njia nyingine ya kutambua uwanja na kazi mbalimbali ni kwa kutumia grafu. Kwa sababu uwanja unahusu seti ya maadili ya pembejeo iwezekanavyo, uwanja wa grafu ina maadili yote ya pembejeo yaliyoonyeshwa kwenye x-axis. Aina ni seti ya maadili ya pato iwezekanavyo, ambayo yanaonyeshwa kwenye mhimili wa y. Kumbuka kwamba ikiwa grafu inaendelea zaidi ya sehemu ya grafu tunaweza kuona, uwanja na upeo unaweza kuwa mkubwa kuliko maadili inayoonekana. Angalia Kielelezo\(\PageIndex{7}\).
![[Grafu ya polynomial inayoonyesha x-axis ni uwanja na y-axis ni upeo]](https://math.libretexts.org/@api/deki/files/878/CNX_Precalc_Figure_01_02_006.jpg)
Tunaweza kuona kwamba grafu inaenea kwa usawa kutoka -5 hadi kulia bila kufungwa, hivyo uwanja ni\(\left[−5,∞\right)\). Kiwango cha wima cha grafu ni maadili yote 5 na chini, hivyo upeo ni\(\left(−∞,5\right]\). Kumbuka kuwa kikoa na upeo daima huandikwa kutoka kwa ndogo hadi maadili makubwa, au kutoka kushoto kwenda kulia kwa kikoa, na kutoka chini ya grafu hadi juu ya grafu kwa upeo.
Mfano\(\PageIndex{6A}\): Finding Domain and Range from a Graph
Pata uwanja na aina mbalimbali ya kazi ya ambayo grafu inavyoonekana kwenye Mchoro 1.2.8.
![[Grafu ya kazi kutoka (-3, 1].]](https://math.libretexts.org/@api/deki/files/879/CNX_Precalc_Figure_01_02_007.jpg)
Suluhisho
Tunaweza kuona kwamba kiwango usawa wa grafu ni -3 kwa 1, hivyo uwanja wa f ni\(\left(−3,1\right]\).
Kiwango cha wima cha grafu ni 0 hadi -4, hivyo upeo ni\(\left[−4,0\right)\). Angalia Kielelezo\(\PageIndex{9}\).
![[Grafu ya kazi ya awali inaonyesha uwanja na upeo.]](https://math.libretexts.org/@api/deki/files/880/CNX_Precalc_Figure_01_02_008.jpg)
Mfano\(\PageIndex{6B}\): Finding Domain and Range from a Graph of Oil Production
Pata uwanja na aina mbalimbali ya kazi ya ambayo grafu inavyoonekana kwenye Kielelezo\(\PageIndex{10}\).
![[Grafu ya Alaska Crude Oil Production ambapo y-mhimili ni mapipa elfu kwa siku na -mhimili ni miaka.]](https://math.libretexts.org/@api/deki/files/881/CNX_Precalc_Figure_01_02_009.jpg)
Suluhisho
Kiasi cha pembejeo kando ya mhimili usio na usawa ni “miaka,” ambayo tunawakilisha na t ya kutofautiana kwa muda. Kiasi cha pato ni “maelfu ya mapipa ya mafuta kwa siku,” ambayo tunawakilisha na b ya kutofautiana kwa mapipa. Grafu inaweza kuendelea upande wa kushoto na kulia zaidi ya kile kinachotazamwa, lakini kulingana na sehemu ya grafu inayoonekana, tunaweza kuamua uwanja kama\(1973≤t≤2008\) na upeo kama takriban\(180≤b≤2010\).
Katika maelezo ya muda, uwanja ni\([1973, 2008]\), na upeo ni juu\([180, 2010]\). Kwa uwanja na upeo, tunakaribia maadili madogo na makubwa zaidi kwani hazianguka hasa kwenye mistari ya gridi ya taifa.
Zoezi\(\PageIndex{6}\)
Kutokana Kielelezo\(\PageIndex{11}\), kutambua uwanja na upeo kwa kutumia muda notation.
![[Grafu ya Kuongezeka kwa idadi ya watu duniani ambapo y-axis inawakilisha mamilioni ya watu na x-axis inawakilisha mwaka.]](https://math.libretexts.org/@api/deki/files/882/CNX_Precalc_Figure_01_02_010.jpg)
- Jibu
-
uwanja =\([1950,2002]\)
masafa =\([47,000,000,89,000,000]\)
![]() Je, uwanja wa kazi na upeo unaweza kuwa sawa?
Je, uwanja wa kazi na upeo unaweza kuwa sawa?
Ndiyo. Kwa mfano, uwanja na upeo wa kazi ya mizizi ya mchemraba ni seti ya namba zote halisi.
Kutafuta Domains na Ranges ya Kazi za Toolkit
Sasa tutarudi kwenye seti yetu ya kazi za toolkit ili kuamua uwanja na upeo wa kila mmoja.
![[Kazi ya mara kwa mara f (x) =c.]](https://math.libretexts.org/@api/deki/files/883/CNX_Precalc_Figure_01_02_011.jpg)
Kwa kazi ya mara kwa mara\( f(x)=c\), uwanja una namba zote halisi; hakuna vikwazo kwenye pembejeo. Thamani pekee ya pato ni ya mara kwa mara\(c\), hivyo upeo ni seti\(\{c\}\) ambayo ina kipengele hiki kimoja. Katika maelezo ya muda, hii imeandikwa kama\([c,c]\), muda ambao wote huanza na kuishia na\(c\).
![[Utambulisho kazi f (x) =x.]](https://math.libretexts.org/@api/deki/files/884/CNX_Precalc_Figure_01_02_012.jpg)
Kielelezo\(\PageIndex{13}\): Kazi ya utambulisho f (x) =x.
Kwa kazi ya utambulisho\(f(x)=x\), hakuna kizuizi juu ya\(x\). Wote kikoa na upeo ni seti ya namba zote halisi.
![[Kazi kamili f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
Kwa kazi kamili ya thamani\(f(x)=|x|\), hakuna kizuizi juu ya\(x\). Hata hivyo, kwa sababu thamani kamili hufafanuliwa kama umbali kutoka 0, pato inaweza tu kuwa kubwa kuliko au sawa na 0.
![[quadratic kazi f (x) =x ^ 2]](https://math.libretexts.org/@api/deki/files/886/CNX_Precalc_Figure_01_02_014.jpg)
Kwa kazi ya quadratic\(f(x)=x^2\), uwanja ni namba zote halisi tangu kiwango cha usawa cha grafu ni mstari wa namba halisi. Kwa sababu grafu haijumuishi maadili yoyote hasi kwa upeo, upeo ni nambari halisi zisizo na hasi tu.
![[Kazi za ujazo f (x) -x ^ 3.]](https://math.libretexts.org/@api/deki/files/887/CNX_Precalc_Figure_01_02_015.jpg)
Kwa kazi ya ujazo\(f(x)=x^3\), uwanja ni namba zote halisi kwa sababu kiwango cha usawa cha grafu ni mstari wa namba halisi. Hali hiyo inatumika kwa kiwango cha wima cha grafu, hivyo uwanja na upeo hujumuisha namba zote halisi.
![[Kazi ya kurudisha f (x) =1/x.]](https://math.libretexts.org/@api/deki/files/888/CNX_Precalc_Figure_01_02_016.jpg)
Kwa kazi ya kurudia\(f(x)=\dfrac{1}{x}\), hatuwezi kugawanya na 0, kwa hiyo tunapaswa kuwatenga 0 kutoka kwenye kikoa. Zaidi ya hayo, 1 imegawanywa na thamani yoyote haiwezi kamwe kuwa 0, hivyo upeo pia hautajumuisha 0. Katika kuweka wajenzi nukuu, tunaweza pia kuandika\(\{x| x≠0\}\), seti ya idadi yote halisi ambayo si sifuri.
![[Kazi ya mraba inayofaa...]](https://math.libretexts.org/@api/deki/files/889/CNX_Precalc_Figure_01_02_017.jpg)
Kwa kazi ya mraba ya usawa\(f(x)=\dfrac{1}{x^2}\), hatuwezi kugawanya na 0, kwa hiyo tunapaswa kuwatenga 0 kutoka kwenye kikoa. Pia hakuna x ambayo inaweza kutoa pato la 0, hivyo 0 ni kutengwa kutoka mbalimbali pia. Kumbuka kuwa pato la kazi hii daima ni chanya kutokana na mraba katika denominator, hivyo upeo unajumuisha namba nzuri tu.
![[Mizizi ya mraba kazi f (x) =sqrt (x).]](https://math.libretexts.org/@api/deki/files/890/CNX_Precalc_Figure_01_02_018.jpg)
Kielelezo\(\PageIndex{19}\): Kazi ya mizizi ya mraba\(f(x)=\sqrt{(x)}\).
Kwa kazi ya mizizi ya mraba\(f(x)=\sqrt{x}\), hatuwezi kuchukua mizizi ya mraba ya nambari halisi ya hasi, hivyo uwanja lazima uwe 0 au zaidi. Mipangilio pia haijumuishi namba hasi kwa sababu mizizi ya mraba ya nambari nzuri\(x\) hufafanuliwa kuwa chanya, ingawa mraba wa namba hasi\(−\sqrt{x}\) pia unatupa\(x\).
![[Kazi ya mizizi ya mchemraba f (x) =x^ (1/3).]](https://math.libretexts.org/@api/deki/files/891/CNX_Precalc_Figure_01_02_019.jpg)
Kwa kazi ya mizizi ya mchemraba\(f(x)=\sqrt[3]{x}\), uwanja na upeo ni pamoja na namba zote halisi. Kumbuka kuwa hakuna tatizo kuchukua mizizi mchemraba, au yoyote isiyo ya kawaida-integer mizizi, ya idadi hasi, na matokeo ya matokeo ni hasi (ni kazi isiyo ya kawaida).
![]() Kutokana na fomu ya kazi, tambua kikoa na upeo.
Kutokana na fomu ya kazi, tambua kikoa na upeo.
- Usiondoe kwenye kikoa maadili yoyote ya pembejeo ambayo husababisha mgawanyiko na sifuri.
- Usiondoe kwenye kikoa maadili yoyote ya pembejeo ambayo hayana matokeo ya nambari ya kweli (au isiyojulikana).
- Tumia maadili ya pembejeo halali ili kuamua maadili mbalimbali ya pato.
- Angalia grafu ya kazi na maadili ya meza ili kuthibitisha tabia halisi ya kazi.
Kutafuta Domain na Range Kutumia Kazi za Toolkit
Kupata uwanja na aina mbalimbali ya\(f(x)=2x^3−x\).
Suluhisho
Hakuna vikwazo kwenye kikoa, kama nambari yoyote halisi inaweza kuwa cubed na kisha kuondolewa kutoka matokeo.
Kikoa ni\((−\infty,\infty)\) na upeo pia\((−\infty,\infty)\).
Mfano\(\PageIndex{7B}\): Finding the Domain and Range
Kupata uwanja na aina mbalimbali ya\(f(x)=\frac{2}{x+1}\).
Suluhisho
Hatuwezi kutathmini kazi katika -1 kwa sababu mgawanyiko kwa sifuri haujafafanuliwa. Kikoa ni\((−\infty,−1)\cup(−1,\infty)\). Kwa sababu kazi haijawahi sifuri, tunaondoa 0 kutoka kwa upeo. Mipangilio ni\((−\infty,0)\cup(0,\infty)\).
Mfano\(\PageIndex{7C}\): Finding the Domain and Range
Kupata uwanja na aina mbalimbali ya\(f(x)=2 \sqrt{x+4}\).
Suluhisho
Hatuwezi kuchukua mizizi mraba ya idadi hasi, hivyo thamani ndani ya radical lazima nonnegative.
\(x+4≥0\)lini\(x≥−4\)
uwanja wa\(f(x)\) ni\([−4,\infty)\).
Sisi kisha kupata mbalimbali. Tunajua kwamba\(f(−4)=0\), na thamani ya kazi\(x\) huongezeka kama ongezeko bila kikomo chochote cha juu. Tunahitimisha kwamba aina mbalimbali ya f ni\(\left[0,\infty\right)\).
Uchambuzi
Kielelezo\(\PageIndex{19}\) inawakilisha kazi\(f\).
 " src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
" src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
Zoezi\(\PageIndex{7}\)
Pata uwanja na aina mbalimbali
\(f(x)=\sqrt{−2−x}\).
- Jibu
-
kikoa:\(\left(−\infty,-2\right]\)
mbalimbali:\(\left[0,\infty\right)\)
Graphing Kipande Defined Kazi
Wakati mwingine, sisi kuja katika kazi ambayo inahitaji formula zaidi ya moja ili kupata pato kutokana. Kwa mfano, katika kazi za toolkit, tulianzisha kazi ya thamani kamili\(f(x)=|x|\). Kwa uwanja wa namba zote halisi na maadili mbalimbali zaidi kuliko au sawa na 0, thamani kamili inaweza kuelezwa kama ukubwa, au moduli, ya thamani halisi ya idadi bila kujali ishara. Ni umbali kutoka 0 kwenye mstari wa namba. Ufafanuzi huu wote unahitaji pato kuwa kubwa kuliko au sawa na 0.
Kama sisi pembejeo 0, au thamani chanya, pato ni sawa na pembejeo.
\[ f(x)=x \; \text{ if } \; x≥0 \nonumber \]
Ikiwa tunaingiza thamani hasi, pato ni kinyume cha pembejeo.
\[ f(x) = -x \; \text { if } \; x < 0 \nonumber \]
Kwa sababu hii inahitaji michakato miwili tofauti au vipande, kazi ya thamani kamili ni mfano wa kazi ya kipande. Kazi ya kipande ni kazi ambayo formula zaidi ya moja hutumiwa kufafanua pato juu ya vipande tofauti vya kikoa.
Tunatumia kazi za kipande kuelezea hali ambazo utawala au uhusiano hubadilika kama thamani ya pembejeo inavuka “mipaka” fulani. Kwa mfano, sisi mara nyingi hukutana na hali katika biashara ambayo gharama kwa kila kipande cha kipengee fulani imepunguzwa mara nambari iliyoamriwa inazidi thamani fulani. Mabano ya kodi ni mfano mwingine wa ulimwengu halisi wa kazi za kipande. Kwa mfano, fikiria mfumo rahisi wa kodi ambao mapato hadi $10,000 yanatakiwa kwa 10%, na mapato yoyote ya ziada yanatakiwa kwa asilimia 20. Kodi ya jumla ya mapato S itakuwa\(0.1S\) kama\(S≤$10,000\) na\($1000+0.2(S−$10,000)\) kama\(S>$10,000\).
Kipande kazi
Kazi ya kipande ni kazi ambayo formula zaidi ya moja hutumiwa kufafanua pato. Kila formula ina uwanja wake mwenyewe, na uwanja wa kazi ni umoja wa nyanja hizi zote ndogo. Tunaona wazo hili kama hili:
\[f(x)= \begin{cases} \text{formula 1} & \text{if x is in domain 1} \\ \text{formula 2} &\text{if x is in domain 2} \\ \text{formula 3} &\text{if x is in domain 3}\end{cases} \nonumber \]
Katika nukuu ya kipande, kazi ya thamani kamili ni
\[|x|= \begin{cases} x & \text{if $x \geq 0$} \\ -x &\text{if $x<0$} \end{cases} \nonumber \]
![]() Kutokana na kazi ya kipande, weka fomu na utambue kikoa kwa kila muda.
Kutokana na kazi ya kipande, weka fomu na utambue kikoa kwa kila muda.
- Tambua vipindi ambavyo sheria tofauti zinatumika.
- Tambua formula zinazoelezea jinsi ya kuhesabu pato kutoka kwa pembejeo katika kila kipindi.
- Tumia braces na kama-kauli kuandika kazi.
Mfano\(\PageIndex{8A}\): Writing a Piecewise Function
Makumbusho hulipa $5 kwa kila mtu kwa ziara ya kuongozwa na kundi la watu 1 hadi 9 au ada ya $50 kwa kundi la watu 10 au zaidi. Andika kazi inayohusiana na idadi ya watu\(n\),, kwa gharama,\(C\).
Suluhisho
Njia mbili tofauti zitahitajika. Kwa\(n\) -maadili chini ya 10,\(C=5n\). Kwa maadili ya n ambayo ni 10 au zaidi,\(C=50\).
\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]
Uchambuzi
Kazi inawakilishwa katika Kielelezo\(\PageIndex{20}\). Grafu ni mstari wa diagonal kutoka\(n=0\) kwa\(n=10\) na mara kwa mara baada ya hapo. Katika mfano huu, kanuni mbili zinakubaliana wakati wa mkutano ambapo\(n=10\), lakini sio kazi zote za kipande zina mali hii.
![[Grafu ya C (n).]](https://math.libretexts.org/@api/deki/files/894/CNX_Precalc_Figure_01_02_021.jpg)
Mfano\(\PageIndex{8B}\): Working with a Piecewise Function
Kampuni ya simu ya mkononi inatumia kazi hapa chini ili kuamua gharama, C, kwa dola kwa g gigabytes ya uhamisho wa data.
\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]
Pata gharama ya kutumia gigabytes 1.5 ya data na gharama ya kutumia gigabytes 4 za data.
Suluhisho
Ili kupata gharama ya kutumia gigabytes 1.5 ya data\(C(1.5)\), sisi kwanza kuangalia kuona ni sehemu gani ya uwanja pembejeo yetu iko katika. Kwa sababu 1.5 ni chini ya 2, tunatumia formula ya kwanza.
\[C(1.5)=$25 \nonumber \]
Ili kupata gharama ya kutumia gigabytes 4 za data, C (4), tunaona kwamba pembejeo yetu ya 4 ni kubwa kuliko 2, kwa hiyo tunatumia formula ya pili.
\[C(4)=25+10(4−2)=$45 \nonumber \]
Uchambuzi
Kazi inawakilishwa katika Kielelezo\(\PageIndex{21}\). Tunaweza kuona ambapo kazi mabadiliko kutoka mara kwa mara kwa kubadilishwa na aliweka utambulisho katika\(g=2\). Tunapanga grafu kwa fomu tofauti kwenye seti ya kawaida ya axes, kuhakikisha kila formula inatumiwa kwenye uwanja wake sahihi.
![[Grafu ya C (g)]](https://math.libretexts.org/@api/deki/files/895/CNX_Precalc_Figure_01_02_022.jpg)
![]() Kutokana na kazi ya kipande, mchoro grafu.
Kutokana na kazi ya kipande, mchoro grafu.
- Eleza kwenye x-axis mipaka iliyoelezwa na vipindi kwenye kila kipande cha kikoa.
- Kwa kila kipande cha uwanja, grafu juu ya muda huo kwa kutumia equation sambamba yanayohusiana na kipande hicho. Je, si graph kazi mbili juu ya muda mmoja kwa sababu ingekuwa kukiuka vigezo vya kazi.
Mfano\(\PageIndex{8C}\): Graphing a Piecewise Function
Mchoro grafu ya kazi.
\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]
Suluhisho
Kila moja ya kazi sehemu ni kutoka maktaba yetu ya kazi toolkit, hivyo tunajua maumbo yao. Tunaweza kufikiria kuchora kila kazi na kisha kupunguza grafu kwenye uwanja ulioonyeshwa. Katika mwisho wa kikoa, tunapata miduara ya wazi ili kuonyesha ambapo mwisho haujumuishwa kwa sababu ya usawa wa chini au mkubwa zaidi; tunapata mduara uliofungwa ambapo mwisho umejumuishwa kwa sababu ya chini-kuliko-au-sawa-kwa au kubwa-kuliko-sawa-kwa usawa.
Kielelezo\(\PageIndex{20}\) inaonyesha sehemu tatu za kazi piecewise graphed juu ya mifumo tofauti kuratibu.
![[Grafu ya kila sehemu ya kazi ya kipande-busara f (x)]](https://math.libretexts.org/@api/deki/files/896/CNX_Precalc_Figure_01_02_023abc.jpg)
Kielelezo\(\PageIndex{20}\): Grafu ya kila sehemu ya kazi ya busara ya kipande f (x)
(a)\( f(x)=x^2\) kama\(x≤1\); (b)\(f(x)=3\) kama\(1< x≤2\); (c)\(f(x)=x\) kama\(x>2\)
Sasa kwa kuwa tumeweka kila kipande moja kwa moja, tunawachanganya katika ndege sawa ya kuratibu. Angalia Kielelezo\(\PageIndex{21}\).
![[Grafu ya kazi nzima.]](https://math.libretexts.org/@api/deki/files/897/CNX_Precalc_Figure_01_02_026.jpg)
Uchambuzi
Kumbuka kwamba grafu haina kupita mstari wima mtihani hata katika\(x=1\) na\(x=2\) kwa sababu pointi\((1,3)\) na\((2,2)\) si sehemu ya grafu ya kazi, ingawa\((1,1)\) na\((2, 3)\) ni.
Zoezi\(\PageIndex{8}\)
Grafu zifuatazo piecewise kazi.
\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]
- Jibu
-
![[Grafu ya f (x).]](https://math.libretexts.org/@api/deki/files/898/CNX_Precalc_Figure_01_02_027.jpg)
Kielelezo\(\PageIndex{22}\)
![]() Je, formula zaidi ya moja kutoka kwa kazi ya kipande inaweza kutumika kwa thamani katika uwanja?
Je, formula zaidi ya moja kutoka kwa kazi ya kipande inaweza kutumika kwa thamani katika uwanja?
Hapana. Kila thamani inalingana na equation moja katika formula piecewise.
Dhana muhimu
- Kikoa cha kazi kinajumuisha maadili yote ya pembejeo halisi ambayo hayatasababisha sisi kujaribu operesheni isiyojulikana ya hisabati, kama kugawa kwa sifuri au kuchukua mizizi ya mraba ya namba hasi.
- Kikoa cha kazi kinaweza kuamua kwa kuorodhesha maadili ya pembejeo ya seti ya jozi zilizoamriwa.
- Uwanja wa kazi pia unaweza kuamua kwa kutambua maadili ya pembejeo ya kazi iliyoandikwa kama equation.
- Maadili ya muda yaliyowakilishwa kwenye mstari wa nambari yanaweza kuelezewa kwa kutumia notation ya usawa, notation ya kuweka-wajenzi, na notation ya muda.
- Kwa kazi nyingi, uwanja na upeo unaweza kuamua kutoka kwenye grafu.
- Uelewa wa kazi za toolkit unaweza kutumika kupata uwanja na aina mbalimbali za kazi zinazohusiana.
- Kazi ya kipande ni ilivyoelezwa na formula zaidi ya moja.
- Kazi ya kipande inaweza kupigwa kwa kutumia kila formula ya algebraic kwenye subdomain yake iliyotolewa.
maelezo ya chini
1 Hesabu: Ambapo Data na Movie Business Meet. “Sanduku la Historia ya Ofisi ya Horror. http://www.the-numbers.com/market/genre/Horror. Iliyopatikana 3/24/2014
2 www.eia.gov/Dnav/pet/Hist/lea... s=mcrfpak2&f=A.
faharasa
- nukuu ya muda
-
njia ya kuelezea seti inayojumuisha namba zote kati ya kikomo cha chini na kikomo cha juu; maadili ya chini na ya juu yameorodheshwa kati ya mabano au mabano, bracket ya mraba inayoonyesha kuingizwa katika seti, na mabano yanayoonyesha kutengwa
- kazi ya kipande
-
kazi ambayo formula zaidi ya moja hutumiwa kufafanua pato
- kuweka-wajenzi nukuu
-
njia ya kuelezea seti na sheria ambayo wanachama wake wote wanatii; inachukua fomu {x| statement kuhusu x}


