15.3: Mzunguko rahisi wa AC
- Page ID
- 176551
Mwishoni mwa sehemu hiyo, utaweza:
- Tafsiri michoro za phasor na uitumie kwenye nyaya za ac na resistors, capacitors, na inductors
- Eleza majibu ya kupinga, capacitor, na inductor ili kusaidia kuelewa jinsi sasa katika mzunguko inavyofanya ikilinganishwa na kila moja ya vifaa hivi
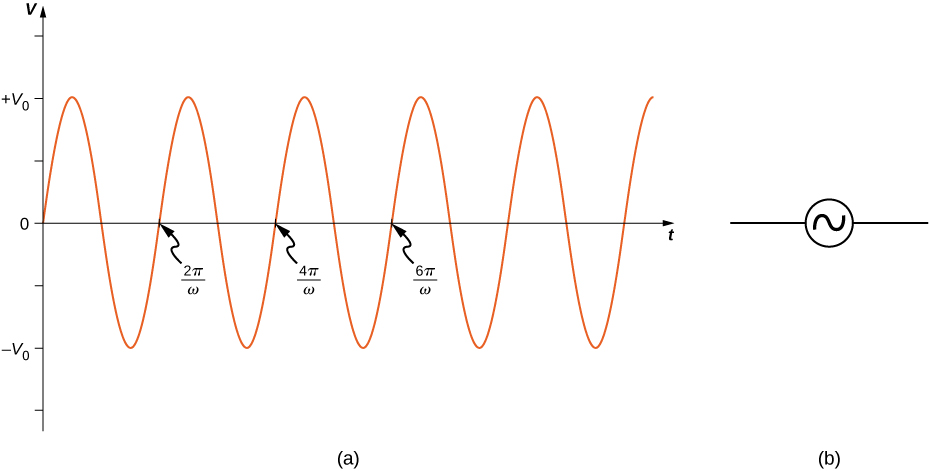
Katika sehemu hii, tunasoma mifano rahisi ya vyanzo vya voltage vya ac vinavyounganishwa na vipengele vitatu vya mzunguko: (1) kupinga, (2) capacitor, na (3) inductor. Nguvu inayotengenezwa na chanzo cha voltage ya ac ina emf iliyotolewa na
\[v(t) = V_0 \, sin \, \omega t,\]
kama inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kazi hii sine akubali sisi kuanza kurekodi voltage\(v = 0 \, V\) wakati ni wakati wa\(t = 0 \, s\). Mara kwa mara ya awamu inaweza kuhusishwa kwamba mabadiliko ya kazi wakati sisi kuanza kupima voltages, sawa na awamu ya mara kwa mara katika mawimbi tuliyojifunza katika Waves. Hata hivyo, kwa sababu sisi ni huru kuchagua wakati sisi kuanza kuchunguza voltage, tunaweza kupuuza awamu hii mara kwa mara kwa sasa. Tunaweza kupima voltage hii katika vipengele vya mzunguko kwa kutumia moja ya njia mbili: (1) mbinu ya upimaji kulingana na ujuzi wetu wa nyaya, au (2) mbinu ya graphical inayoelezwa katika sehemu zijazo.
Mshindani
Kwanza, fikiria kupinga kushikamana kwenye chanzo cha voltage ya ac. Kutoka kwa utawala wa kitanzi cha Kirchhoff, voltage instantaneous katika kupinga ya Kielelezo\(\PageIndex{2a}\) ni
\[v_R(t) = V_0 \, sin \, \omega t\]
na sasa instantaneous kupitia resistor ni
\[i_R(t) = \frac{v_R(t)}{R} = \frac{V_0}{R} \, sin \, \omega t = I_0 \, sin \, \omega t.\]
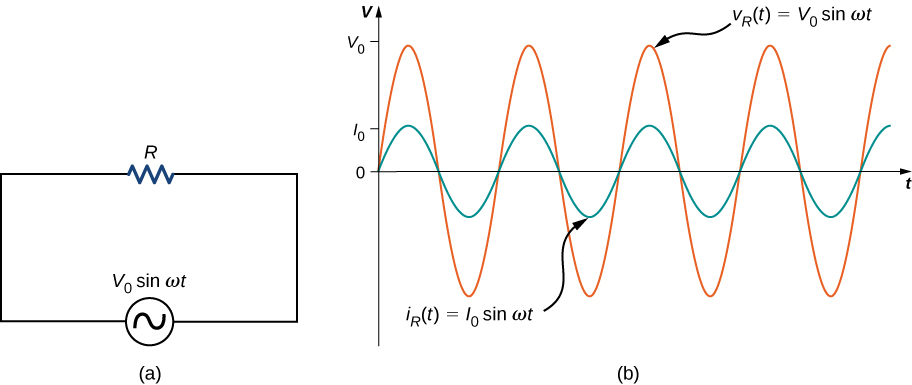
Hapa,\(I_0 = V_0/R\) ni amplitude ya sasa ya kutofautiana wakati. Viwanja\(i_R(t)\) na\(v_R(t)\) ni inavyoonekana katika Kielelezo\(\PageIndex{2b}\). Vipande vyote vinafikia maxima yao na minima kwa nyakati moja, yaani, sasa kupitia na voltage katika kupinga ni katika awamu.
Uwakilishi wa picha ya mahusiano ya awamu kati ya sasa na voltage mara nyingi ni muhimu katika uchambuzi wa nyaya za ac. Uwakilishi huo huitwa michoro za awamu. Mchoro wa phasor\(i_R(t)\) umeonyeshwa kwenye Mchoro\(\PageIndex{3a}\), na sasa kwenye mhimili wima. Mshale (au phasor) unazunguka kinyume chake kwa mzunguko wa angular mara kwa mara\(\omega\), kwa hiyo tunaiangalia kwa papo moja kwa wakati. Ikiwa urefu wa mshale unafanana na amplitude ya sasa\(I_0\), makadirio ya mshale unaozunguka kwenye mhimili wima ni\(i_R(t) = I_0 \, sin \, \omega t\), ambayo ni ya sasa ya haraka.
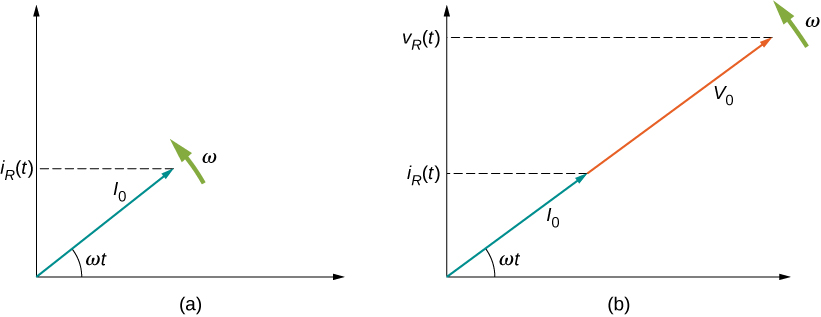
Mhimili wima kwenye mchoro wa awamu inaweza kuwa ama voltage au ya sasa, kulingana na awamu inayochunguzwa. Kwa kuongeza, kiasi kadhaa kinaweza kuonyeshwa kwenye mchoro huo wa awamu. Kwa mfano, wote wa sasa\(i_R(t)\) na voltage\(v_R(t)\) huonyeshwa kwenye mchoro wa Kielelezo\(\PageIndex{3b}\). Kwa kuwa wana mzunguko sawa na wako katika awamu, phasors zao zinaelekeza katika mwelekeo huo na kuzunguka pamoja. Urefu wa jamaa wa phasors mbili ni kiholela kwa sababu huwakilisha kiasi tofauti; hata hivyo, uwiano wa urefu wa phasors mbili unaweza kuwakilishwa na upinzani, kwa kuwa moja ni phasor ya voltage na nyingine ni awamu ya sasa.
Capacitor
Sasa hebu tuchunguze capacitor iliyounganishwa kwenye chanzo cha voltage ya ac. Kutoka kwa utawala wa kitanzi cha Kirchhoff, voltage ya papo hapo katika capacitor ya Kielelezo\(\PageIndex{4a}\) ni
\[v_C(t) = V_0 \, sin \, \omega t.\]
Kumbuka kwamba malipo katika capacitor hutolewa na\(Q = CV\). Hii ni kweli wakati wowote kipimo katika mzunguko wa ac wa voltage. Kwa hiyo, malipo ya papo hapo juu ya capacitor ni
\[q(t) = Cv_C(t) = CV_0 \, sin \, \omega t.\]
Tangu sasa katika mzunguko ni kiwango ambacho malipo huingia (au majani) capacitor,
\[i_C(t) = \frac{dq(t)}{dt} = \omega CV_0 \, cos \, \omega t = I_0 \, cos \, \omega t,\]
\(I_0 = \omega CV_0\)wapi amplitude ya sasa. Kutumia uhusiano wa trigonometric\(cos \, \omega t = sin (\omega t + \pi/2)\), tunaweza kueleza sasa instantaneous kama
\[i_C(t) = I_0 \, sin \left(\omega t + \frac{\pi}{2}\right).\]
Kugawanyika\(V_0\) na\(I_0\), tunapata equation inayoonekana sawa na sheria ya Ohm:
\[\frac{V_0}{I_0} = \frac{1}{\omega C} = X_C. \label{15.3}\]
Kiasi\(X_C\) ni sawa na upinzani katika mzunguko wa dc kwa maana kwamba wingi wote ni uwiano wa voltage hadi sasa. Matokeo yake, wana kitengo sawa, ohm. Kumbuka, hata hivyo, kwamba capacitor maduka na kuruhusiwa nishati ya umeme, wakati resistor dissipates yake. Kiasi\(X_C\) kinajulikana kama mmenyuko wa capacitive wa capacitor, au upinzani wa capacitor kwa mabadiliko ya sasa. Inategemea inversely juu ya mzunguko wa chanzo cha ac- high frequency inaongoza kwa reactance chini capacitive.
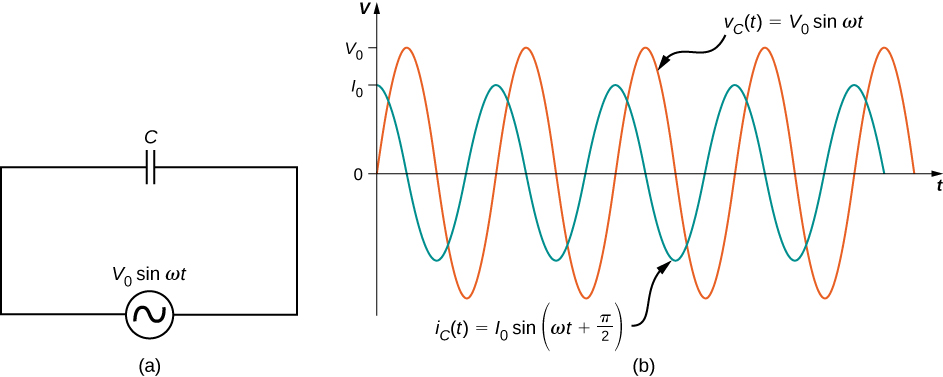
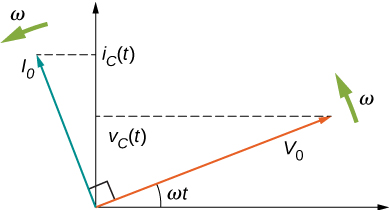
kulinganisha maneno kwa\(v_C(t)\) na\(i_C(t)\) inaonyesha kwamba kuna awamu tofauti ya\(\pi/2\) rad kati yao. Wakati kiasi hizi mbili ni walipanga pamoja, peaks sasa robo mzunguko (au\(\pi/2\) rad) mbele ya voltage, kama mfano katika Kielelezo\(\PageIndex{4b}\). Ya sasa kupitia capacitor inaongoza voltage katika capacitor kwa\(\pi/2\) rad, au robo ya mzunguko.
Mchoro wa awamu sambamba unaonyeshwa kwenye Kielelezo\(\PageIndex{5}\). Hapa, uhusiano kati\(i_C(t)\) na\(v_C(t)\) inawakilishwa na kuwa na phasors yao mzunguko katika mzunguko huo angular, na awamu ya sasa inayoongoza kwa\(\pi/2\) rad.
Kwa hatua hii, tumekuwa tu kutumia maadili ya kilele cha sasa au voltage katika majadiliano yetu, yaani,\(I_0\) na\(V_0\). Hata hivyo, ikiwa sisi wastani wa maadili ya sasa au voltage, maadili haya ni sifuri. Kwa hiyo, sisi mara nyingi kutumia mkataba wa pili kuitwa mizizi maana thamani mraba, au thamani RMS, katika majadiliano ya sasa na voltage. RMS inafanya kazi kinyume cha istilahi. Kwanza, wewe mraba kazi, ijayo, unachukua maana, na kisha, unapata mizizi ya mraba. Matokeo yake, maadili ya rms ya sasa na voltage sio sifuri. Vifaa na vifaa ni kawaida alinukuliwa na maadili RMS kwa shughuli zao, badala ya maadili kilele. Tunaonyesha maadili ya RMS na usajili unaohusishwa na barua kuu (kama vile\(I_{rms}\)).
Ingawa capacitor kimsingi ni mzunguko wa wazi, sasa ya rms, au mraba wa maana ya mizizi ya sasa, inaonekana katika mzunguko na voltage ya ac kutumika kwa capacitor. Fikiria kwamba
\[I_{rms} = \frac{I_0}{\sqrt{2}},\]
\(I_0\)wapi kilele cha sasa katika mfumo wa ac. Voltage RMS, au mizizi maana mraba wa voltage, ni
\[V_{rms} = \frac{V_0}{\sqrt{2}},\]
\(V_0\)wapi voltage kilele katika mfumo wa ac. Sasa RMS inaonekana kwa sababu voltage inaendelea kugeuka, kumshutumu, na kuruhusu capacitor. Ikiwa mzunguko unakwenda sifuri, ambayo itakuwa voltage ya dc,\(X_C\) huelekea infinity, na sasa ni sifuri mara moja capacitor inashtakiwa. Katika masafa ya juu sana, mmenyuko wa capacitor huelekea sifuri-ina majibu yasiyo na maana na hauzuii sasa (inafanya kama waya rahisi).
Inductor
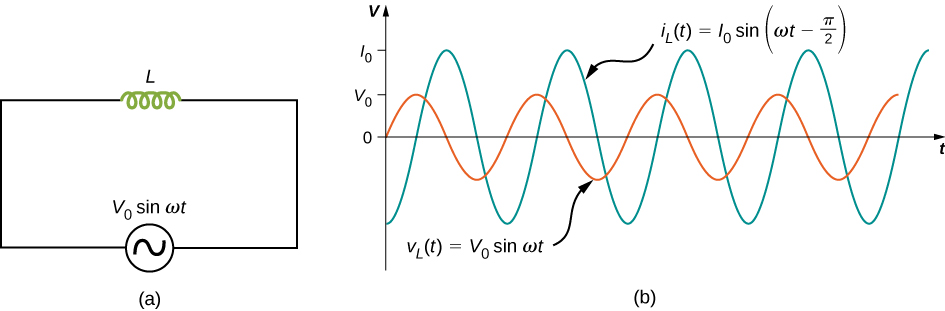
Hatimaye, hebu tuchunguze inductor iliyounganishwa na chanzo cha voltage ya ac. Kutoka kwa utawala wa kitanzi cha Kirchhoff, voltage katika inductor L ya Kielelezo\(\PageIndex{6a}\) ni
\[v_L(t) = V_0 \, sin \, \omega t. \label{15.6}\]
EMF katika inductor ni sawa na\(\epsilon = - L(di_L/dt)\); Hata hivyo, tofauti tofauti katika inductor ni\(v_L(t) = Ldi_L(t)/dt\), kwa sababu ikiwa tunaona kwamba voltage karibu kitanzi lazima iwe sawa na sifuri, voltage iliyopatikana kutoka chanzo cha ac inapaswa kuenea kupitia inductor. Kwa hiyo, kuunganisha hii na chanzo cha voltage ya ac, tuna
\[\frac{di_L(t)}{dt} = \frac{V_0}{L} \, sin \, \omega t.\]
Ya sasa\(i_L(t)\) inapatikana kwa kuunganisha equation hii. Kwa kuwa mzunguko hauna chanzo cha emf mara kwa mara, hakuna sasa ya kutosha katika mzunguko. Kwa hiyo, tunaweza kuweka mara kwa mara ya ushirikiano, ambayo inawakilisha sasa ya kutosha katika mzunguko, sawa na sifuri, na tuna
\[i_L(t) = - \frac{V_0}{\omega L} cos \, \omega t = \frac{V_0}{\omega L} sin \left(\omega t - \frac{\pi}{2}\right) = I_0 \, sin \left(\omega t - \frac{\pi}{2}\right), \label{15.7}\]
wapi\(I_0 = V_0/\omega L\). Uhusiano kati\(V_0\) na pia\(I_0\) unaweza kuandikwa kwa fomu inayofanana na sheria ya Ohm:
\[\frac{V_0}{I_0} = \omega L = X_L. \label{15.8}\]
Kiasi\(X_L\) kinajulikana kama mmenyuko wa inductor, au upinzani wa inductor kwa mabadiliko ya sasa; kitengo chake pia ni ohm. Kumbuka kwamba\(X_L\) inatofautiana moja kwa moja kama mzunguko wa AC chanzo - high frequency husababisha high inductive majibu.
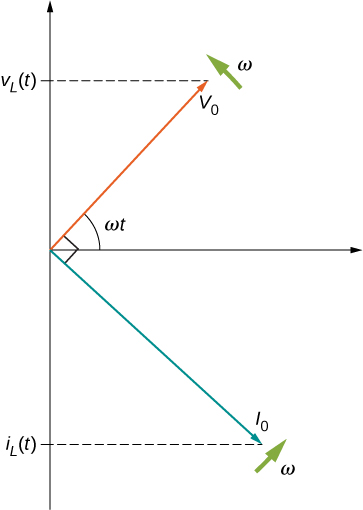
Tofauti ya awamu ya\(\pi/2\) rad hutokea kati ya sasa kupitia na voltage katika inductor. Kutoka Equation\ ref {15.6} na Equation\ ref {15.7}, sasa kwa njia ya inductor lipo tofauti uwezo katika inductor na\(\pi/2\) rad, au robo ya mzunguko. Mchoro wa awamu kwa kesi hii umeonyeshwa kwenye Kielelezo\(\PageIndex{7}\).
uhuishaji kutoka Chuo Kikuu cha New South Wales AC Circuits unaeleza baadhi ya dhana sisi kujadili katika sura hii. Pia ni pamoja na wimbi na phasor michoro kwamba kubadilika baada ya muda ili uweze kupata picha bora ya jinsi kila mabadiliko baada ya muda.
Jenereta ya ac inazalisha emf ya amplitude 10 V kwa mzunguko\(f = 60 \, Hz\). Kuamua voltages kote na mikondo kupitia vipengele vya mzunguko wakati jenereta imeunganishwa na (a)\(100 \, \Omega\) kupinga, (b)\(10 \, \mu F\) capacitor, na (c) inductor 15-mH.
Mkakati
Voltage nzima ya AC katika kila kifaa ni sawa na voltage ya chanzo. Tunaweza kupata mikondo kwa kutafuta reactance X ya kila kifaa na kutatua kwa sasa kilele kutumia\(I_0 = V_0/X\).
Suluhisho
Voltage katika vituo vya chanzo ni
\[v(t) = V_0 \, sin \, \omega t = (10 \, V) sin \, 120 \pi t,\]
\(\omega = 2\pi f = 120 \pi \, rad/s\)wapi mzunguko wa angular. Tangu v (t) pia voltage katika kila moja ya mambo, tuna
\[v(t) = v_R(t) = v_C(t) = v_L(t) = (10 \, V) sin \, 120 \pi t.\]
a Wakati\(R = 100 \, \Omega\), amplitude ya sasa kwa njia ya kupinga ni
\[I_0 = V_0/R = 10 \, V/100 \, \Omega = 0.10 \, A,\]hivyo
\[i_R(t) = (0.10 \, A) sin \, 120 \pi t.\]
b Kutoka Equation\ ref {15.3}, mmenyuko wa capacitive ni
\[X_C = \frac{1}{\omega C} = \frac{1}{(120 \pi \, rad/s)(10 \times 10^{-6}F)} = 265 \, \Omega,\]
hivyo thamani ya juu ya sasa ni
\[I_0 = \frac{V_0}{X_C} = \frac{10 \, V}{265 \, \Omega} = 3.8 \times 10^{-2} \, A\]
na sasa instantaneous inatolewa na
\[i_C(t) = (3.8 \times 10^{-2} \, A) \, sin \, \left(120 \pi t + \frac{\pi}{2}\right).\]
c Kutoka Equation\ ref {15.8}, mmenyuko wa inductive ni
\[ X_L = \omega L = (120 \pi \, rad/s)(15 \times 10^{-3} H) = 5.7 \, \Omega.\]
Upeo wa sasa ni kwa hiyo
\[I_0 = \frac{10 \, V}{5.7 \, \Omega} = 1.8 \, A\]
na sasa instantaneous ni
\[i_L(t) = (1.8 \, A) \, sin \left(120 \pi t - \frac{\pi}{2}\right).\]
Umuhimu
Ingawa voltage katika kila kifaa ni sawa, sasa kilele kina maadili tofauti, kulingana na majibu. Mchanganyiko wa kila kifaa hutegemea maadili ya upinzani, capacitance, au inductance.
Rudia Mfano\(\PageIndex{1}\) kwa chanzo cha ac cha amplitude 20 V na mzunguko 100 Hz.
- Jibu
-
a.\((20 \, V) \, sin \, 200 \pi t\),\((0.20 \, A) \, sin \, 200 \pi t\);
b.\((20 \, V) \, sin \, 200 \pi t\),\((0.13 \, A) \, sin \, (200\pi t + \pi /2)\);
c.\((20 \, V) \, sin \, 200 \pi t\),\((2.1 \, A) \, sin \, (200 \pi t - \pi/2)\)


