13.7: Jenereta za Umeme na Emf ya nyuma

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza jinsi jenereta ya umeme inavyofanya kazi
• Kuamua emf ikiwa katika kitanzi wakati wowote wakati, kupokezana kwa kiwango cha mara kwa mara katika uwanja wa magnetic
• Onyesha kwamba coils zinazozunguka zina emf inayoingizwa; katika motors hii inaitwa nyuma emf kwa sababu inapinga pembejeo ya emf kwa motor.

Matukio mbalimbali muhimu na vifaa vinaweza kueleweka na sheria ya Faraday. Katika sehemu hii, tunachunguza mbili kati ya hizi.

Jenereta za umeme

Jenereta za umeme zinashawishi emf kwa kupokezana coil katika uwanja wa magnetic, kama ilivyojadiliwa kwa ufupi katika Emf ya Motional. Sasa tunachunguza jenereta kwa undani zaidi. Fikiria mfano unaofuata.

Kuhesabu Emf Incuded katika Coil Generator

Coil ya jenereta iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1}\) imezungushwa kupitia moja ya nne ya mapinduzi (kutoka\(\theta = 0^o\) kwa\(\theta = 90^o\)) katika 15.0 ms. Coil 200 ya mviringo ina radius 5.00-cm na iko katika sare 0.80-T magnetic shamba. Je, ni emf ikiwa ni nini?

Kielelezo\(\PageIndex{1}\): Wakati coil hii ya jenereta inapozungushwa kupitia moja ya nne ya mapinduzi,\(\Phi_m\) mabadiliko ya magnetic yanabadilika kutoka upeo wake hadi sifuri, na kusababisha emf.

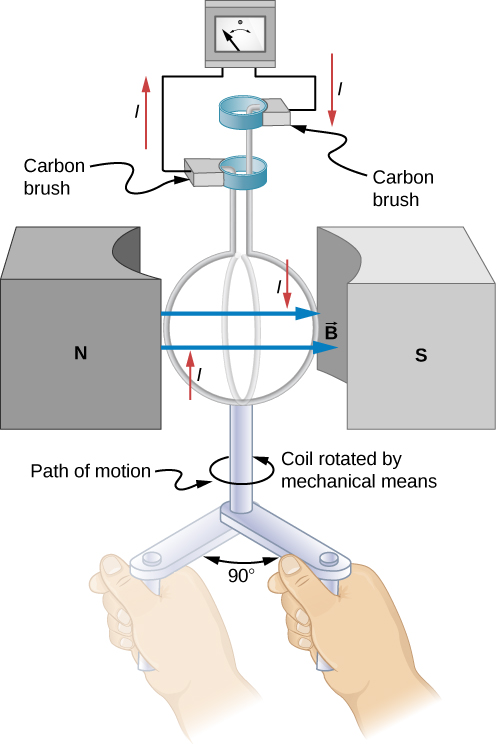
Mkakati

Sheria ya Faraday ya induction hutumiwa kupata emf ikiwa:

\[\epsilon = - N\frac{d\Phi_m}{dt}.\]

Tunatambua hali hii kama moja katika Mfano 13.4.3. Kwa mujibu wa mchoro, makadirio ya vector ya kawaida ya uso\(\hat{n}\) kwenye shamba la magnetic ni ya awali\(cos \, \theta\) na hii imeingizwa na ufafanuzi wa bidhaa ya dot. Ukubwa wa shamba la magnetic na eneo la kitanzi ni fasta kwa muda, ambayo inafanya ushirikiano iwe rahisi haraka. EMF iliyosababishwa imeandikwa kwa kutumia sheria ya Faraday:

\[\epsilon = NBA \, sin \, \theta \frac{d\theta}{dt}.\]

Suluhisho Tunapewa kwamba\(N = 200,\)\(B = 0.80 \, T\)\(\theta = 90^o\),,\(d\theta = 90^o = \pi /2\), na\(dt = 15.0 \, ms\). Eneo la kitanzi ni

\[A = \pi r^2 = (3.14)(0.0500 \, m)^2 = 7.85 \times 10^{-3} \, m^2.\]

Kuingia thamani hii inatoa

\[\epsilon = (200)(0.80 \, T)(7.85 \times 10^{-3} \, m^2) sin (90^o) \frac{\pi/2}{15.0 \times 10^{-3} s} = 131 \, V.\]

Umuhimu

Hii ni thamani ya wastani ya vitendo, sawa na 120 V iliyotumiwa katika nguvu za kaya.

EMF mahesabu katika Mfano\(\PageIndex{1}\) ni wastani juu ya moja ya nne ya mapinduzi. Je, ni emf kwa papo yoyote? Inatofautiana na angle kati ya shamba la magnetic na perpendicular kwa coil. Tunaweza kupata kujieleza kwa emf kama kazi ya muda kwa kuzingatia emf motional juu ya kupokezana mstatili coil ya upana w na urefu l katika uwanja sare magnetic, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\): Jenereta yenye coil moja ya mstatili inayozungushwa kwa kasi ya angular mara kwa mara katika uwanja wa sare ya magnetic hutoa emf ambayo inatofautiana sinusoidally kwa wakati. Kumbuka jenereta ni sawa na motor, isipokuwa shimoni ni kuzungushwa kuzalisha sasa badala ya njia nyingine kote.

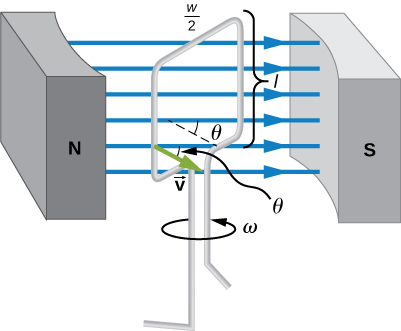
Malipo katika waya wa kitanzi hupata nguvu ya magnetic, kwa sababu wanahamia kwenye uwanja wa magnetic. Malipo katika waya wima uzoefu vikosi sambamba na waya, na kusababisha mikondo. Lakini wale walio katika makundi ya juu na ya chini wanahisi nguvu perpendicular kwa waya, ambayo haina kusababisha sasa. Tunaweza hivyo kupata emf ikiwa kwa kuzingatia tu waya upande. Emf ya motional inapewa kuwa\(\epsilon = Blv\), ambapo kasi v ni perpendicular kwa shamba magnetic B. Hapa kasi ni kwa pembeni\(\theta\) na B, ili sehemu yake perpendicular kwa B ni v dhambi\(\theta\) (angalia Kielelezo\(\PageIndex{2}\)). Kwa hiyo, katika kesi hii, emf ikiwa kila upande ni\(\epsilon = Blv \, sin \, \theta\) na wao ni katika mwelekeo huo. EMF jumla karibu kitanzi ni basi

\[\epsilon = 2 Blv \, sin \, \theta.\]

Maneno haya ni halali, lakini haitoi emf kama kazi ya muda. Ili kupata utegemezi wa muda wa emf, tunadhani coil inazunguka kwa kasi ya angular ya mara kwa mara\(\omega\). Angle\(\theta\) ni kuhusiana na kasi ya angular na\(\theta = \omega t\), ili\[\epsilon = 2 Blv \, sin (\omega t).\]

Sasa, linear kasi v ni kuhusiana na kasi angular\(\omega\) na\(v = r\omega\). Hapa\(r = \omega/2\), ili\(v = (\omega/2)\omega\), na

\[\epsilon = 2Bl \frac{\omega}{2} \omega \, sin \, \omega t = (l\omega) Bw \, sin \, \omega t.\]

Akibainisha kuwa eneo la kitanzi ni\(A = l\omega\), na kuruhusu kwa loops N, tunaona hiyo

\[\epsilon = NBAw \, sin \, (\omega t).\]

Hii ni emf ikiwa katika coil ya jenereta ya N inarudi na eneo A kupokezana kwa kasi ya angular mara kwa mara\(ω\) katika uwanja sare ya magnetic B. Hii pia inaweza kuwa walionyesha kama

\[\epsilon = \epsilon_0 \, sin \, \omega t,\]wapi

\[\epsilon_0 = NAB\omega\]

ni emf kilele, tangu thamani ya juu ya\(sin (\omega t) = 1\). Kumbuka kuwa mzunguko wa oscillation ni\(f = \omega /2\pi\) na kipindi ni\(T = 1/f = 2\pi /\omega\). Kielelezo\(\PageIndex{3}\) inaonyesha grafu ya emf kama kazi ya muda, na sasa inaonekana busara kwamba voltage ac ni sinusoidal.

Kielelezo\(\PageIndex{3}\): EMF ya jenereta inatumwa kwenye bomba la mwanga na mfumo wa pete na maburusi yaliyoonyeshwa. Grafu hutoa emf ya jenereta kama kazi ya wakati,\(\epsilon_0\) wapi emf ya kilele. Kipindi ni\(T = 1/f = 2\pi /\omega\), ambapo f ni mzunguko.

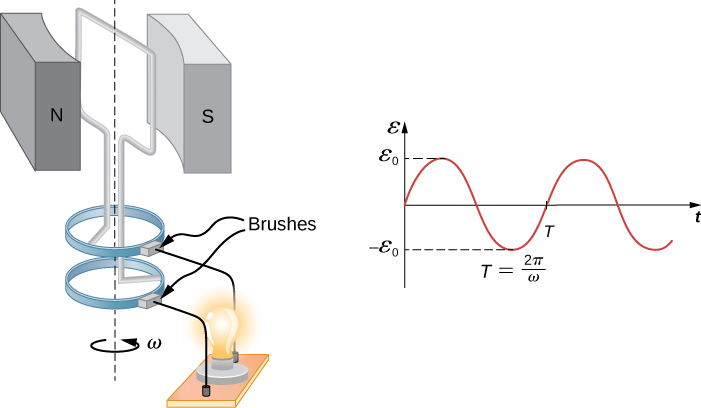
Ukweli kwamba emf kilele ni\(\epsilon_0 = NBA\omega\) mantiki nzuri. Idadi kubwa ya coils, eneo lao kubwa, na shamba lenye nguvu, zaidi ya voltage ya pato. Inashangaza kwamba kasi ya jenereta ni spun (kubwa ω), zaidi ya emf. Hii inaonekana juu ya jenereta za baiskeli-angalau aina za bei nafuu.

Kielelezo\(\PageIndex{4}\) kinaonyesha mpango ambao jenereta inaweza kufanywa ili kuzalisha pulsed dc. Mipango ya kufafanua zaidi ya coils nyingi na pete za kupasuliwa zinaweza kuzalisha DC laini, ingawa elektroniki badala ya njia za mitambo hutumiwa kutengeneza dc ya bure.

Kielelezo\(\PageIndex{4}\): Split pete, kuitwa commutators, kuzalisha pulsed dc emf pato katika Configuration hii.

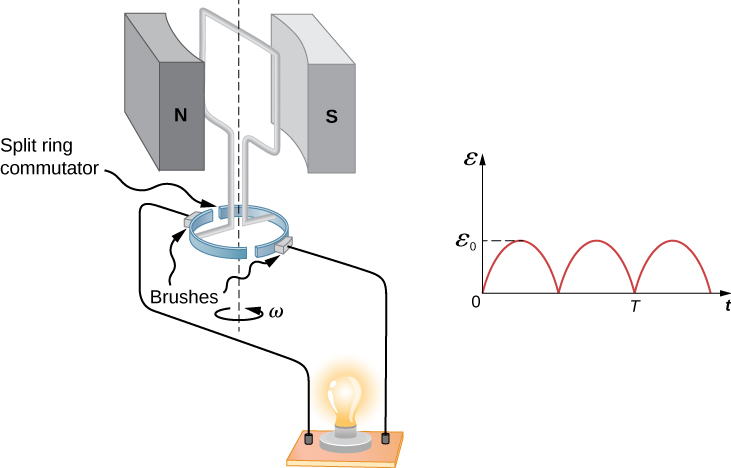
Katika maisha halisi, jenereta za umeme zinaonekana tofauti sana na takwimu katika sehemu hii, lakini kanuni ni sawa. Chanzo cha nishati ya mitambo ambayo inarudi coil inaweza kuwa maji ya kuanguka (hydropower), mvuke zinazozalishwa na kuchomwa kwa mafuta ya mafuta, au nishati ya kinetic ya upepo. Kielelezo\(\PageIndex{5}\) kinaonyesha mtazamo wa cutaway wa turbine ya mvuke; mvuke huenda juu ya vile vilivyounganishwa na shimoni, ambayo huzunguka coil ndani ya jenereta. Kizazi cha nishati ya umeme kutoka nishati ya mitambo ni kanuni ya msingi ya nguvu zote zinazotumwa kupitia gridi zetu za umeme kwenye nyumba zetu.

Kielelezo\(\PageIndex{5}\): Steam turbine/jenereta. Mvuke unaozalishwa na kuchomwa makaa ya mawe huathiri vile vya turbine, na kugeuka shimoni, iliyounganishwa na jenereta.

Jenereta zilizoonyeshwa katika sehemu hii zinaonekana sana kama motors zilizoonyeshwa hapo awali. Hii si kwa bahati mbaya. Kwa kweli, motor inakuwa jenereta wakati shimoni yake inazunguka. Baadhi ya magari mapema kutumika motor yao starter kama jenereta. Katika sehemu inayofuata, tunachunguza zaidi hatua ya motor kama jenereta.

Back Emf

Jenereta hubadilisha nishati ya mitambo katika nishati ya umeme, ambapo motors hubadilisha nishati ya umeme kuwa nishati ya mitambo. Hivyo, haishangazi kwamba motors na jenereta zina ujenzi huo wa jumla. Motor hufanya kazi kwa kutuma sasa kupitia kitanzi cha waya kilicho kwenye uwanja wa magnetic. Matokeo yake, uwanja wa magnetic hufanya wakati juu ya kitanzi. Hii huzunguka shimoni, na hivyo kuchimba kazi ya mitambo nje ya sasa ya umeme iliyotumwa awali. (Rejea Nguvu na Torque juu ya Loop sasa kwa ajili ya majadiliano juu ya motors ambayo itasaidia kuelewa zaidi kuhusu wao kabla ya kuendelea.)

Wakati coil ya motor imegeuka, flux magnetic inabadilika kupitia coil, na emf (sambamba na sheria ya Faraday) inaingizwa. Kwa hiyo motor hufanya kama jenereta wakati wowote coil yake inazunguka. Hii hutokea kama shimoni inageuka na pembejeo ya nje, kama gari la ukanda, au kwa hatua ya motor yenyewe. Hiyo ni, wakati motor inafanya kazi na shimoni yake inageuka, emf huzalishwa. Sheria ya Lenz inatuambia EMF inapinga mabadiliko yoyote, ili emf ya pembejeo inayowezesha motor inapingana na emf ya motor inayozalishwa yenyewe, inayoitwa emf ya nyuma ya motor (Kielelezo\(\PageIndex{6}\)).

Kielelezo\(\PageIndex{6}\): Coil ya motor dc inawakilishwa kama kupinga katika schematic hii. EMF ya nyuma inawakilishwa kama emf ya kutofautiana ambayo inapinga emf kuendesha gari. Back emf ni sifuri wakati motor si kugeuka na kuongezeka kwa uwiano na kasi ya angular motor.

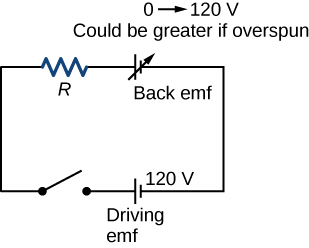
Pato la jenereta la motor ni tofauti kati ya voltage ya usambazaji na emf ya nyuma. Emf ya nyuma ni sifuri wakati motor inapogeuka kwanza, maana yake ni kwamba coil inapata voltage kamili ya kuendesha gari na motor huchota sasa upeo wakati ni juu lakini si kugeuka. Kama motor inarudi kwa kasi, emf ya nyuma inakua, daima inapinga emf ya kuendesha gari, na inapunguza voltage zote kwenye coil na kiasi cha sasa kinachochota. Athari hii inaonekana katika hali nyingi za kawaida. Wakati kusafisha utupu, jokofu, au mashine ya kuosha ni ya kwanza, taa katika mzunguko huo hupungua kwa ufupi kutokana na kushuka kwa IR zinazozalishwa katika mistari ya feeder na sasa kubwa inayotolewa na motor.

Wakati motor kwanza inakuja, huchota zaidi ya sasa kuliko wakati inaendesha kasi yake ya kawaida ya uendeshaji. Wakati mzigo wa mitambo umewekwa kwenye motor, kama gurudumu la umeme linakwenda juu ya kilima, motor hupungua, matone ya nyuma ya emf, mtiririko wa sasa zaidi, na kazi zaidi inaweza kufanyika. Ikiwa motor inaendesha kasi ya chini sana, sasa kubwa inaweza kuifanya (kupitia nguvu ya kupinga kwenye coil\(P = I^2R)\), labda hata kuwaka). Kwa upande mwingine, ikiwa hakuna mzigo wa mitambo kwenye motor, huongeza kasi yake ya angular ω mpaka emf ya nyuma iko karibu sawa na emf ya kuendesha gari. Kisha motor hutumia nishati tu ya kutosha kushinda msuguano.

Maji ya Eddy katika cores ya chuma ya motors inaweza kusababisha hasara za nishati ngumu. Hizi ni kawaida kupunguzwa kwa kujenga cores nje ya karatasi nyembamba, umeme maboksi ya chuma. Mali ya magnetic ya msingi hayaathiriwa na uharibifu wa karatasi ya kuhami, wakati inapokanzwa kwa kupinga kunapungua kwa kiasi kikubwa. Fikiria, kwa mfano, coils motor kuwakilishwa katika Kielelezo\(\PageIndex{6}\). Coils na upinzani sawa\(0.400 \, \Omega\) na inaendeshwa na emf ya 48.0 V. muda mfupi baada ya kugeuka, wao kuteka sasa

\[I = V/R = (48.0 \, V)/(0.400 \, \Omega) = 120 \, A\]

na hivyo dissipate\(P = I^2R = 5.76 \, kW\) ya nishati kama uhamisho joto. Chini ya hali ya kawaida ya uendeshaji kwa motor hii, tuseme emf nyuma ni 40.0 V. kisha kwa kasi ya uendeshaji, voltage jumla katika coils ni 8.0 V (48.0 V bala 40.0 V nyuma emf), na sasa inayotolewa ni

\[I = V/R = (8.0 \, V)/(0.400 \, \Omega) = 20 \, A.\]

Chini ya mzigo wa kawaida, basi, nguvu imeshuka ni\(P = IV = (20 \, A)(8.0 \, V) = 160 \, W\). Hii haina kusababisha tatizo kwa motor hii, wakati wa zamani 5.76 kW ingekuwa kuchoma nje coils kama endelevu.

Mfululizo wa Jeraha la Mfululizo Katika Uendeshaji

Upinzani\((R_f + R_a)\) wa jumla wa motor ya jeraha la mfululizo ni\(2.0 \, \Omega\) (Kielelezo\(\PageIndex{7}\)). Unapounganishwa na chanzo cha 120-V\((\epsilon_S)\), motor huchota 10 A wakati wa kukimbia kwa kasi ya angular mara kwa mara. (a) Ni nini nyuma EMF ikiwa katika coil kupokezana,\(\epsilon_i\)? (b) Je, ni pato la nguvu ya mitambo ya motor? (c) Ni kiasi gani cha nguvu kinachopotea katika upinzani wa coils? (d) Pato la nguvu la chanzo cha 120-V ni nini? (e) Tuseme mzigo juu ya ongezeko motor, na kusababisha kupungua kwa uhakika ambapo huchota 20 A. sehemu Jibu (a) kwa njia ya (d) kwa hali hii.

Kielelezo\(\PageIndex{7}\): Uwakilishi wa mzunguko wa mfululizo wa jeraha moja kwa moja ya sasa.

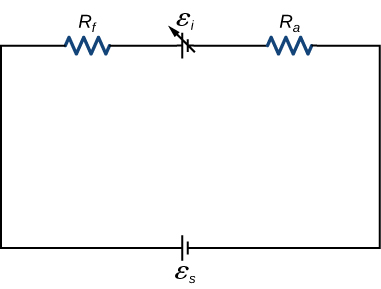
Mkakati

Emf ya nyuma imehesabiwa kulingana na tofauti kati ya voltage iliyotolewa na kupoteza kutoka kwa sasa kupitia upinzani. Nguvu kutoka kwa kila kifaa imehesabiwa kutoka kwa mojawapo ya fomu za nguvu kulingana na taarifa iliyotolewa.

Suluhisho

1. EMF nyuma ni\[\epsilon_i = \epsilon_S - I(R_f + RE_a) = 120 \, V - (10 \, A)(2.0 \, \Omega) = 100 \, V.\]
2. Kwa kuwa uwezo katika silaha ni 100 V wakati sasa kwa njia hiyo ni 10 A, pato la nguvu la motor ni\[P_m = \epsilon_i I = (100 \, V)(10 \, A) = 1.0 \times 10^3 \, W.\]
3. Ya sasa 10-A inapita kupitia coils ambao upinzani pamoja ni\(2.0 \, \Omega\), hivyo nguvu dissipated katika coils ni\[P_R = I^2R = (10 \, A)^2(2.0 \, \Omega) = 2.0 \times 10^2 \, W.\]
4. Tangu 10 A hutolewa kutoka chanzo cha 120-V, pato lake la nguvu ni\[P_S = \epsilon_S I = (120 \, V)(10 \, A) = 1.2 \times 10^3 \, W.\]
5. Kurudia mahesabu sawa na\(I = 20 \, A\), tunapata\[\epsilon_i = 80 \, V, \, P_m = 1.6 \times 10^3 \, W, \, P_R = 8.0 \times 10^2 \, W, \, and \, P_s = 2.4 \times 10^3 \, W.\] Motor inageuka polepole zaidi katika kesi hii, hivyo pato lake la nguvu na nguvu ya chanzo ni kubwa.

Umuhimu Taarifa kwamba tuna uwiano wa nishati katika sehemu (d):\[1.2 \times 10^3 \, W = 1.0 \times 10^3 \, W + 2.0 \times 10^2 \, W.\]