Skip to main content
Global

10.6: RC Circuits

  1. Last updated
  2. Save as PDF
  • Page ID
    175667

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hiyo, utaweza:

    • Eleza mchakato wa malipo ya capacitor
    • Eleza mchakato wa kuruhusu wa capacitor
    • Andika orodha ya baadhi ya programu za nyaya za RC

    Unapotumia kamera ya flash, inachukua sekunde chache kulipa capacitor inayowezesha flash. Flash ya mwanga hutoa capacitor katika sehemu ndogo ya pili. Kwa nini malipo huchukua muda mrefu kuliko kuruhusu? Swali hili na matukio mengine kadhaa ambayo yanahusisha malipo na kuruhusu capacitors yanajadiliwa katika moduli hii.

    Circuits na Upinzani na Capacitance

    Mzunguko wa RC ni mzunguko ulio na upinzani na uwezo. Kama ilivyowasilishwa katika Capacitance, capacitor ni sehemu ya umeme ambayo huhifadhi malipo ya umeme, kuhifadhi nishati katika uwanja wa umeme.

    Kielelezo\(\PageIndex{1a}\) kinaonyesha mzunguko rahisi wa RC ambao huajiri chanzo cha voltage cha\(ε\) DC (moja kwa moja)\(R\), kupinga\(C\), capacitor, na kubadili nafasi mbili. Mzunguko inaruhusu capacitor kushtakiwa au kuruhusiwa, kulingana na nafasi ya kubadili. Wakati kubadili ni wakiongozwa na nafasi\(A\), mashtaka capacitor, kusababisha mzunguko katika Kielelezo\(\PageIndex{1b}\). Wakati kubadili kunahamishwa kwenye nafasi B, capacitor hutoa kwa njia ya kupinga.

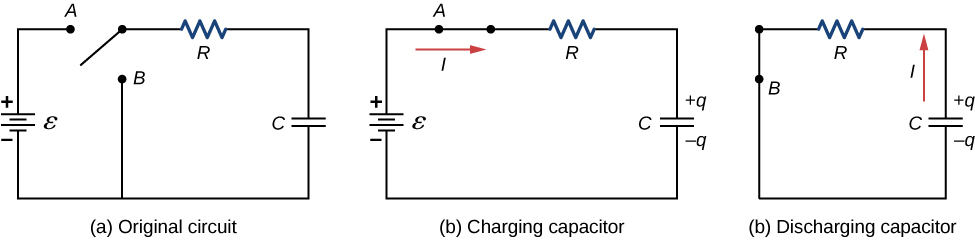
    Sehemu ya A inaonyesha mzunguko wazi na matawi matatu, tawi la kushoto ni chanzo cha voltage na terminal ya juu yenye chanya iliyounganishwa na uhakika A, tawi la kati ni mzunguko mfupi na uhakika B na tawi la kulia ni kupinga na capacitor. Sehemu b inaonyesha mzunguko wa sehemu a na tawi la kwanza kushikamana na tawi la tatu. Sehemu c inaonyesha mzunguko wa sehemu a na tawi la pili kushikamana na tawi la tatu.
    Kielelezo\(\PageIndex{1}\): (a) Mzunguko wa RC na kubadili mbili pole ambayo inaweza kutumika kwa malipo na kutekeleza capacitor. (b) Wakati kubadili kuhamishwa kwenye nafasi A, mzunguko hupunguza uhusiano rahisi wa mfululizo wa chanzo cha voltage, kupinga, capacitor, na kubadili. (c) Wakati kubadili kuhamishwa kwenye nafasi B, mzunguko hupunguza uhusiano rahisi wa mfululizo wa kupinga, capacitor, na kubadili. Chanzo cha voltage kinaondolewa kwenye mzunguko.

    Kushutumu Capacitor

    Tunaweza kutumia utawala wa kitanzi cha Kirchhoff kuelewa malipo ya capacitor. Hii matokeo katika equation\(\epsilon - V_R - V_C = 0\). Equation hii inaweza kutumika kwa mfano malipo kama kazi ya muda kama mashtaka capacitor. Capitance hufafanuliwa kama\(C = q/V\), hivyo voltage katika capacitor ni\(V_C = \frac{q}{C}\). Kutumia sheria ya Ohm, kushuka kwa uwezo katika kupinga ni\(V_R = IR\), na sasa inaelezwa kama\(I = dq/dt\).

    \[\epsilon - V_R - V_C =0,\]

    \[\epsilon - IR - \frac{q}{C} = 0,\]

    \[\epsilon - R\frac{dq}{dt} - \frac{q}{C} = 0.\]

    Equation hii tofauti inaweza kuunganishwa ili kupata equation kwa malipo juu ya capacitor kama kazi ya muda.

    \[\epsilon - R\frac{dq}{dt} - \frac{q}{C} = 0.\]

    \[\frac{dq}{dt} = \frac{\epsilon C - q}{RC},\]

    \[\int_0^q \frac{dq}{\epsilon C - q} = \frac{1}{RC} \int_0^t dt.\]

    Hebu\(u = \epsilon C - q\), basi\(du = -dq\). Matokeo yake ni

    \[-\int_0^q \frac{du}{u} = \frac{1}{RC} \int_0^t dt,\]

    \[\ln \left(\frac{\epsilon C - q}{\epsilon C}\right) = - \frac{1}{RC} t.\]

    \[\frac{\epsilon C - q}{\epsilon C} = e^{-t/RC}.\]

    Kurahisisha matokeo katika equation kwa malipo juu ya malipo capacitor kama kazi ya muda:

    \[q(t) = C\epsilon \left(1 - e^{-\frac{t}{RC}}\right) = Q\left(1 - e^{-\frac{t}{\tau}}\right).\]

    Grafu ya malipo kwenye capacitor dhidi ya wakati inavyoonekana kwenye Mchoro\(\PageIndex{2a}\). Kumbuka kwanza kwamba wakati unakaribia usio na mwisho, ufafanuzi huenda sifuri, hivyo malipo yanakaribia malipo ya juu\(Q = C\epsilon\) na ina vitengo vya coulombs. Vitengo vya RC ni sekunde, vitengo vya wakati. Kiasi hiki kinajulikana kama mara kwa mara ya mara kwa mara:

    \[\tau = RC.\]

    Kwa wakati\(t = \tau = RC\), malipo sawa na\(1 - e^{-1} = 1 - 0.368 = 0.632\) ya malipo ya juu\(Q = C\epsilon\). Kumbuka kwamba mabadiliko ya kiwango cha wakati wa malipo ni mteremko katika hatua ya malipo dhidi ya wakati njama. Mteremko wa grafu ni kubwa kwa wakati\(t - 0.0 \, s\) na unakaribia sifuri kama wakati unavyoongezeka.

    Kama malipo ya capacitor huongezeka, sasa kwa njia ya kupinga hupungua, kama inavyoonekana kwenye Mchoro\(\PageIndex{2b}\). Ya sasa kwa njia ya kupinga inaweza kupatikana kwa kuchukua muda wa malipo.

    \[ \begin{align*} I(t) &= \frac{dq}{dt} \\[4pt] &= \frac{d}{dt}\left[C\epsilon \left( 1 - e^{-\frac{t}{RC}} \right) \right], \\[4pt] &= C\epsilon \left(\frac{1}{RC}\right) e^{-\frac{t}{RC}} \\[4pt] &= \frac{\epsilon}{R} e^{-\frac{t}{TC}} \\[4pt] &= I_0 e^{-\frac{t}{RC}}, \end{align*}\]

    \[I(t) = I_0 e^{-t/\tau}.\]

    Kwa wakati\(t = 0.0 \, s\), sasa kwa njia ya kupinga ni\(I_0 = \frac{\epsilon}{R}\). Kama wakati unakaribia infinity, sasa inakaribia sifuri. Kwa wakati\(t = \tau\), sasa kwa njia ya kupinga ni\(I (t = \tau) = I_0e^{-1} = 0.368 I_0\).

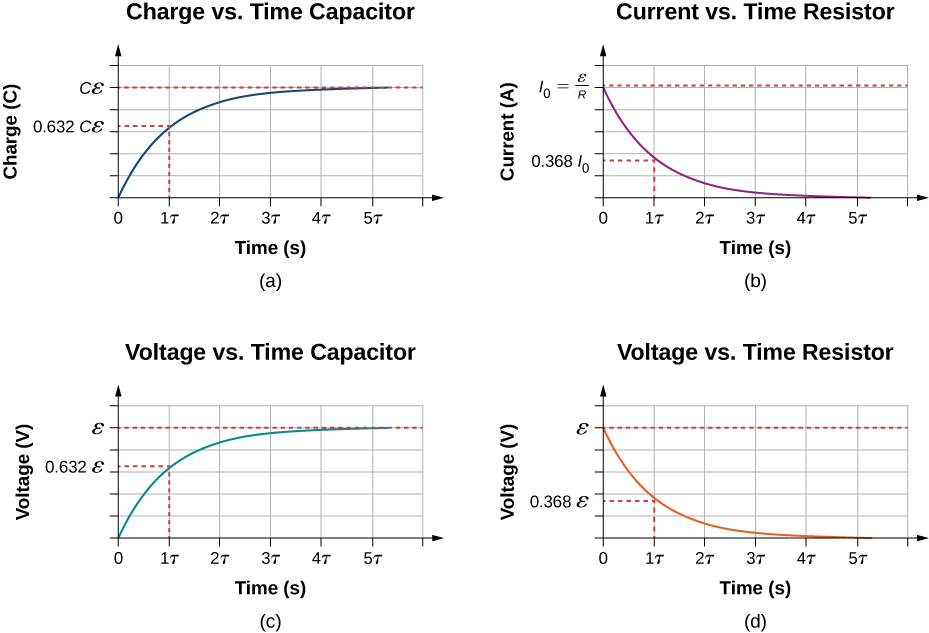
    Takwimu inaonyesha grafu nne za malipo ya capacitor, na wakati kwenye x-axis. Sehemu a inaonyesha malipo ya capacitor kwenye mhimili wa y, thamani huongezeka kutoka 0 hadi Cε na ni sawa na 0.632 Cε baada ya 1 τ. Sehemu b inaonyesha sasa ya kupinga kwenye mhimili wa y, thamani hupungua kutoka kwa mimi kujiandikisha 0 hadi 0 na ni sawa na 0.368 I subscript 0 baada ya 1 τ. Sehemu c inaonyesha voltage ya capacitor kwenye mhimili wa y, thamani huongezeka kutoka 0 hadi ε na ni sawa na 0.632 ε baada ya 1 τ. Sehemu d inaonyesha voltage ya kupinga kwenye mhimili wa y, thamani hupungua kutoka ε hadi 0 na ni sawa na 0.368 ε baada ya 1 τ.
    Kielelezo\(\PageIndex{2}\): (a) Malipo juu ya capacitor dhidi ya muda kama mashtaka capacitor. (b) Sasa kwa njia ya kupinga dhidi ya wakati. (c) Tofauti ya voltage katika capacitor. (d) Tofauti ya voltage katika kupinga.

    Takwimu\(\PageIndex{2c}\) na Kielelezo\(\PageIndex{2d}\) zinaonyesha tofauti za voltage katika capacitor na kupinga, kwa mtiririko huo. Kama malipo ya capacitor huongezeka, sasa hupungua, kama vile tofauti ya voltage katika kupinga\(V_R(t) = (I_0R)e^{-t/\tau} = \epsilon e^{-t/\tau}\). Tofauti ya voltage katika capacitor huongezeka kama\(V_C (t) = \epsilon (1 - e^{-t/\tau} )\).

    Kutekeleza Capacitor

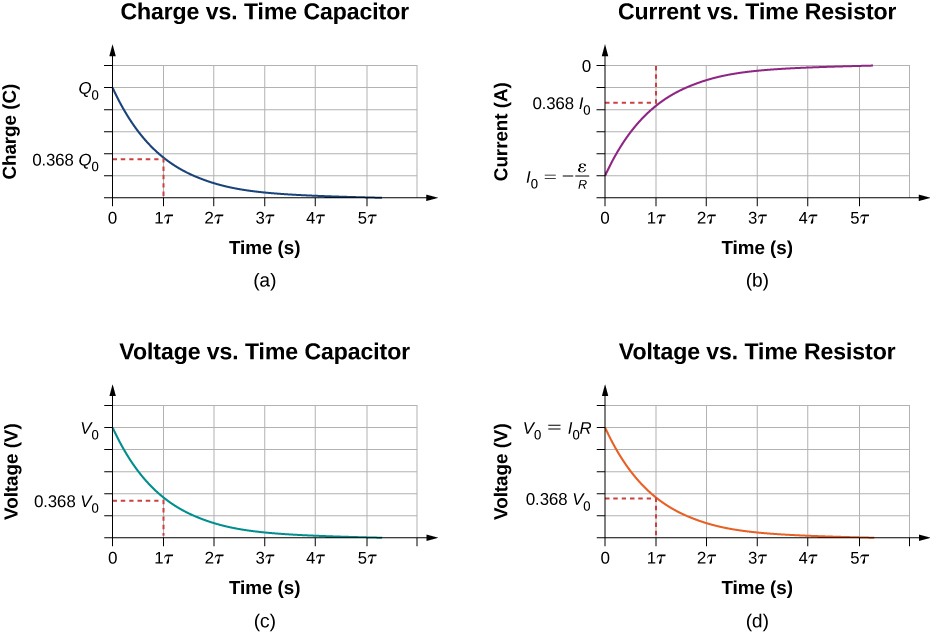
    Wakati kubadili kwenye Kielelezo\(\PageIndex{3a}\) kinahamishwa kwenye nafasi B, mzunguko hupunguza mzunguko kwa sehemu (c), na capacitor ya kushtakiwa inaruhusiwa kutekeleza kupitia kupinga. Grafu ya malipo kwenye capacitor kama kazi ya muda inavyoonekana kwenye Mchoro\(\PageIndex{3a}\). Kutumia utawala wa kitanzi cha Kirchhoff kuchambua mzunguko kama capacitor hutoa matokeo katika equation\(-V_R -V_C = 0\), ambayo simplifies kwa\(IR + \frac{q}{C} = 0\). Kutumia ufafanuzi wa sasa\(\frac{dq}{dt}R = - \frac{q}{C}\) na kuunganisha equation kitanzi hutoa equation kwa malipo juu ya capacitor kama kazi ya muda:

    \[q(t) = Qe^{-t/\tau}.\]

    Hapa, Q ni malipo ya awali kwenye capacitor na\(\tau = RC\) ni mara kwa mara ya mzunguko. Kama inavyoonekana kwenye grafu, malipo hupungua kwa kiasi kikubwa kutoka kwa malipo ya awali, inakaribia sifuri kama wakati unakaribia usio na mwisho.

    Ya sasa kama kazi ya muda inaweza kupatikana kwa kuchukua muda wa malipo:

    \[I(t) = - \frac{Q}{RC}e^{-t/\tau}.\]

    Ishara hasi inaonyesha kwamba sasa inapita katika mwelekeo tofauti wa sasa unaopatikana wakati capacitor inashutumu. Kielelezo\(\PageIndex{3b}\) kinaonyesha mfano wa njama ya malipo dhidi ya muda na sasa dhidi ya wakati. Mpango wa tofauti ya voltage katika capacitor na tofauti ya voltage katika kupinga kama kazi ya muda inavyoonekana katika Takwimu\(\PageIndex{3c}\) na\(\PageIndex{3d}\). Kumbuka kwamba ukubwa wa malipo, sasa, na voltage yote hupungua kwa kiasi kikubwa, inakaribia sifuri kama wakati unavyoongezeka.

    Takwimu inaonyesha grafu nne za capacitor kuruhusu, na wakati kwenye x-axis. Sehemu a inaonyesha malipo ya capacitor kwenye mhimili wa y, thamani hupungua kutoka Q subscript 0 hadi 0 na ni sawa na 0.368 Q subscript 0 baada ya 1 τ. Sehemu b inaonyesha sasa ya kupinga kwenye mhimili wa y, thamani huongezeka kutoka kwa mimi kujiandikisha 0 hadi 0 na ni sawa na 0.368 Ninajiandikisha 0 baada ya 1 τ. Sehemu c inaonyesha voltage ya capacitor kwenye mhimili wa y, thamani inapungua kutoka V subscript 0 hadi 0 na ni sawa na 0.368 V subscript 0 baada ya 1 τ. Sehemu d inaonyesha voltage ya kupinga kwenye mhimili wa y, thamani hupungua kutoka kwa V subscript 0 hadi 0 na ni sawa na 0.368 V subscript 0 baada ya 1 τ.
    Kielelezo\(\PageIndex{3}\): (a) Malipo juu ya capacitor dhidi ya muda kama capacitor kuruhusiwa. (b) Sasa kwa njia ya kupinga dhidi ya wakati. (c) Tofauti ya voltage katika capacitor. (d) Tofauti ya voltage katika kupinga.

    Sasa tunaweza kuelezea kwa nini kamera ya flash iliyotajwa mwanzoni mwa sehemu hii inachukua muda mrefu sana kulipa kuliko kutokwa: Upinzani wakati wa malipo ni mkubwa zaidi kuliko wakati wa kuruhusu. Upinzani wa ndani wa akaunti za betri kwa upinzani zaidi wakati wa malipo. Kama umri wa betri, upinzani wa ndani unaoongezeka hufanya mchakato wa malipo hata polepole.

    Mfano\(\PageIndex{2}\): The Relaxation Oscillator

    Matumizi moja ya mzunguko wa RC ni oscillator ya kufurahi, kama inavyoonekana hapa chini. Oscillator ya kufurahi ina chanzo cha voltage, kupinga, capacitor, na taa ya neon. Taa ya neon hufanya kama mzunguko wazi (upinzani usio na kipimo) mpaka tofauti tofauti katika taa ya neon kufikia voltage maalum. Kwa voltage hiyo, taa hufanya kama mzunguko mfupi (upinzani wa sifuri), na capacitor hutoa kupitia taa ya neon na hutoa mwanga. Katika oscillator relaxation inavyoonekana, chanzo voltage mashtaka capacitor mpaka voltage katika capacitor ni 80 V. wakati hii inatokea, neon katika taa hupungua na inaruhusu capacitor kutekeleza kupitia taa, kuzalisha flash mkali. Baada ya capacitor kikamilifu kuruhusiwa kupitia taa ya neon, huanza kulipa tena, na mchakato unarudia. Kwa kuzingatia kwamba wakati inachukua capacitor kutekeleza ni duni, ni muda gani kati ya flashes?

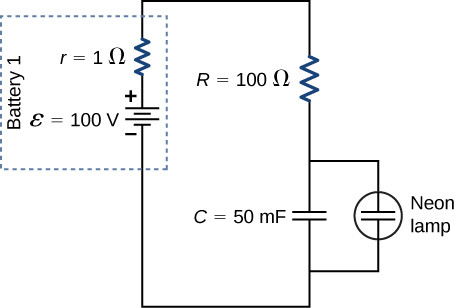
    Chanya terminal ya chanzo cha voltage ya 100 V na upinzani wa ndani wa 1 Ω ni kushikamana na kupinga R ya 100 Ω na capacitor C ya 50 mF. Taa ya neon imeshikamana sawa na capacitor.

    Mkakati

    Kipindi cha muda kinaweza kupatikana kutokana na kuzingatia equation\(V_C(t) = \epsilon (1 - e^{=t/\tau})\). where \(\tau = (R + r)C.\)

    Solution

    The neon lamp flashes when the voltage across the capacitor reaches 80 V. The RC time constant is equal to \(\tau = (R + r) = (101 \, \Omega) (50 \times 10^{-3} F) = 5.05 \, s\). We can solve the voltage equation for the time it takes the capacitor to reach 80 V:

    \[V_C (t) = \epsilon (1 - e^{-t/\tau} ),\]

    \[e^{-t/\tau} = 1 - \frac{V_C(t)}{\epsilon},\]

    \[ln (e^{-t/\tau}) = ln \left(1 - \frac{V_C(t)}{\epsilon} \right),\]

    \[t = -\tau ln \left(1 - \frac{V_C(t)}{\epsilon} \right) = -5.05 \, s \cdot ln \left(1 - \frac{80 \, V}{100 \, V} \right) = 8.13 \, s.\]

    Significance

    One application of the relaxation oscillator is for controlling indicator lights that flash at a frequency determined by the values for R and C. In this example, the neon lamp will flash every 8.13 seconds, a frequency of \( f = \frac{1}{T} = \frac{1}{8.13 \, s} = 0.55 \, Hz\). The relaxation oscillator has many other practical uses. It is often used in electronic circuits, where the neon lamp is replaced by a transistor or a device known as a tunnel diode. The description of the transistor and tunnel diode is beyond the scope of this chapter, but you can think of them as voltage controlled switches. They are normally open switches, but when the right voltage is applied, the switch closes and conducts. The “switch” can be used to turn on another circuit, turn on a light, or run a small motor. A relaxation oscillator can be used to make the turn signals of your car blink or your cell phone to vibrate.

    RC circuits have many applications. They can be used effectively as timers for applications such as intermittent windshield wipers, pace makers, and strobe lights. Some models of intermittent windshield wipers use a variable resistor to adjust the interval between sweeps of the wiper. Increasing the resistance increases the RC time constant, which increases the time between the operation of the wipers.

    Another application is the pacemaker. The heart rate is normally controlled by electrical signals, which cause the muscles of the heart to contract and pump blood. When the heart rhythm is abnormal (the heartbeat is too high or too low), pace makers can be used to correct this abnormality. Pacemakers have sensors that detect body motion and breathing to increase the heart rate during physical activities, thus meeting the increased need for blood and oxygen, and an RC timing circuit can be used to control the time between voltage signals to the heart.

    Looking ahead to the study of ac circuits (Alternating-Current Circuits), ac voltages vary as sine functions with specific frequencies. Periodic variations in voltage, or electric signals, are often recorded by scientists. These voltage signals could come from music recorded by a microphone or atmospheric data collected by radar. Occasionally, these signals can contain unwanted frequencies known as “noise.” RC filters can be used to filter out the unwanted frequencies.

    In the study of electronics, a popular device known as a 555 timer provides timed voltage pulses. The time between pulses is controlled by an RC circuit. These are just a few of the countless applications of RC circuits.

    Example \(\PageIndex{2}\): Intermittent Windshield Wipers

    A relaxation oscillator is used to control a pair of windshield wipers. The relaxation oscillator consists of a 10.00-mF capacitor and a \(10.00 \, k\Omega\) variable resistor known as a rheostat. A knob connected to the variable resistor allows the resistance to be adjusted from \(0.00 \, \Omega\) to \(10.00 \, k\Omega\). The output of the capacitor is used to control a voltage-controlled switch. The switch is normally open, but when the output voltage reaches 10.00 V, the switch closes, energizing an electric motor and discharging the capacitor. The motor causes the windshield wipers to sweep once across the windshield and the capacitor begins to charge again. To what resistance should the rheostat be adjusted for the period of the wiper blades be 10.00 seconds?

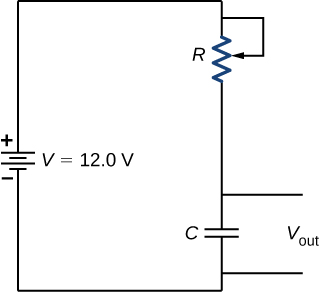
    The positive terminal of voltage source V of 12 V is connected to a variable resistor R and capacitor C. V subscript out is measure across C.

    Mkakati

    Upinzani unazingatia equation\(V_{out}(t) = V(1 - e^{-t/\tau})\), wapi\(\tau = RC\). Capitance, voltage pato, na voltage ya betri hutolewa. Tunahitaji kutatua equation hii kwa upinzani.

    Suluhisho

    Voltage ya pato itakuwa 10.00 V na voltage ya betri ni 12.00 V. uwezo hutolewa kama 10.00 mF. Kutatua kwa mavuno ya upinzani

    \[V_{out}(t) = V(1 - e^{-t/\tau})\]

    \[e^{-t/RC} = 1 - \frac{V_{out}(t)}{V},\]

    \[ln (e^{-t/RC}) = ln \left(1 - \frac{V_{out}(t)}{V} \right),\]

    \[-\frac{t}{RC} = ln \left(1 - \frac{V_{out}(t)}{V} \right),\]

    \[R = \frac{-t}{C \, ln\left( 1 - \frac{V_C(t)}{V}\right)} = \frac{-10.00 \, s}{10 \times 10^{-3} F \, ln \left(1 - \frac{10 \, V}{12 \, V}\right)} = 558.11 \, \Omega.\]

    Umuhimu

    Kuongezeka kwa upinzani huongeza kuchelewa kwa muda kati ya shughuli za wipers za windshield. Wakati upinzani ni sifuri, wipers windshield kukimbia kuendelea. Kwa upinzani wa juu, kipindi cha uendeshaji wa wipers ni:

    \[t = -RC ln\left(1 - \frac{V_{out}(t)}{V}\right) = - (10 \times 10^{-3} F)(10 \times 10^3 \, \Omega) ln \left(1 - \frac{10 \, V}{12 \, V}\right) = 179.18 \, s = 2.98 \, min.\]

    Mzunguko wa RC una maelfu ya matumizi na ni mzunguko muhimu sana kujifunza. Sio tu inaweza kutumika kwa nyaya za muda, inaweza pia kutumika kuchuja masafa zisizohitajika katika mzunguko na kutumika katika vifaa vya nguvu, kama ile ya kompyuta yako, ili kusaidia kugeuka voltage ya ac kwa voltage DC.