7.1: Mteremko wa Mstari
- Page ID
- 164590
Kumbuka kwamba jozi zilizoamriwa zinaweza kupigwa kama pointi katika ndege ya kuratibu mstatili. Kupitia pointi mbili tofauti, graph mstari wa moja kwa moja,\(l\).
Ili kuelezea mstari wa\(l\) algebraically, kwanza fikiria mteremko wa fomu ya mstari.
Mteremko\(m\) wa mstari\(l\) unaopita kupitia pointi\((x_1, y_1)\) na\((x_2, y_2)\) ni
\[m = \dfrac{\text{rise}}{\text{run}} = \dfrac{y_2 − y_1}{x_2 − x_1} \text{ where } x_2 \neq x_1 \nonumber \]
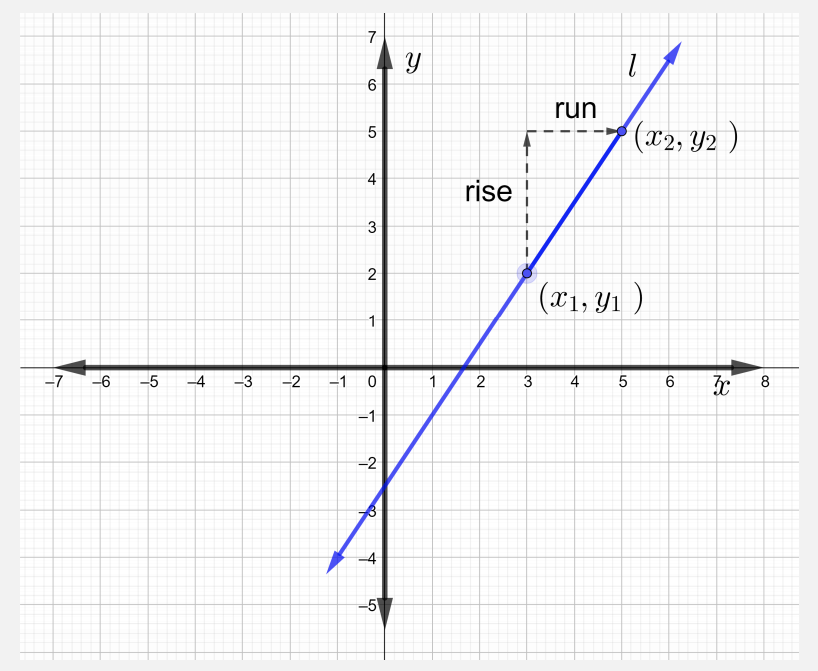
Pata mteremko wa mstari katika takwimu hapa chini.
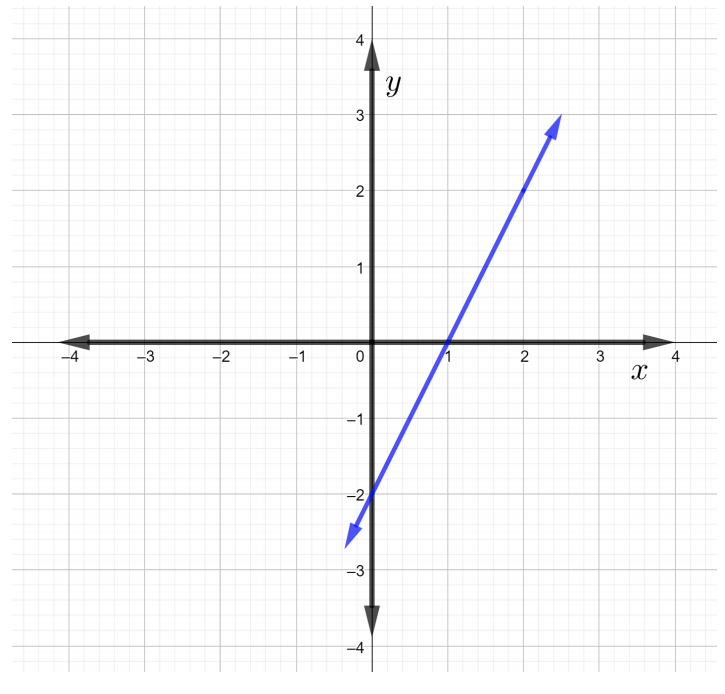
Suluhisho
Kwa ufafanuzi hapo juu wa mteremko wa fomu ya mstari, mteremko wa mstari unaweza kuandikwa kama\(m = \dfrac{\text{rise}}{\text{run}}\). Anza kwa kuchagua pointi mbili,\(P\) na\(Q\), kwenye mstari. Chagua uhakika\(P\) kuwa\((2, 2)\) na uhakika\(Q\) kuwa\((1, 0)\).
Kuanzia saa\(Q\), kupanda hadi hatua\(P\) kwa kuhesabu mraba zaidi ya\(2\) gridi ya taifa, ambayo ina maana\(\text{rise} = 2\). Sasa, ili kufika kwa uhakika\(P\),\(\text{run}\)\(1\) gridi ya mraba kwa haki, ambayo ina maana kwamba\(\text{run} = 1\), kama inavyoonekana katika takwimu hapa chini.
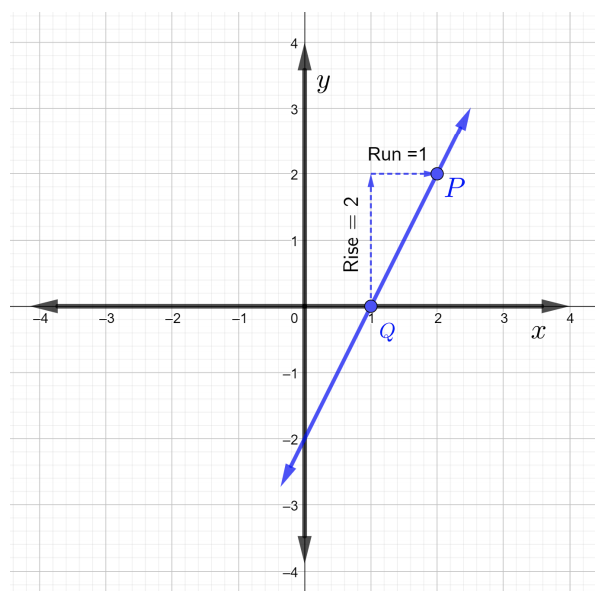
Hivyo,
\(\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{2}{1} &\text{rise \(2\)na kukimbia\(1\)}\\ &= 2\ mwisho {array}\)
Kwa hiyo, mteremko wa mstari katika takwimu ni\(m = 2\).
Pata mteremko wa mstari ulioonyeshwa kwenye takwimu hapa chini.
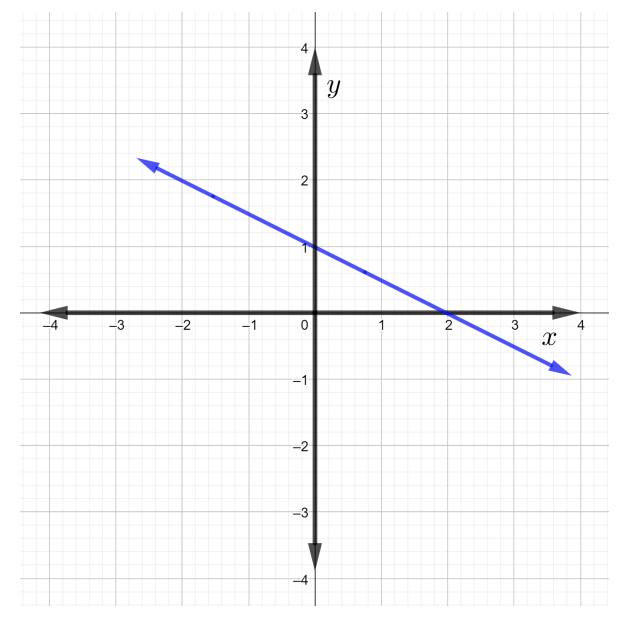
Suluhisho
Sawa na Mfano\(1\), kuanza kwa kuchagua pointi yoyote mbili\(Q\),\(P\) na, kwenye mstari.
Kumbuka: Kwa kuwa\(2\) pointi yoyote kwenye mstari inaweza kuchaguliwa, itakuwa rahisi kuchagua pointi mbili ambazo ni integers. Vipengele hivyo viko kwenye mstari na pia kwenye makutano ya mistari miwili ya gridi ya taifa. Kwa mfano, katika takwimu itakuwa rahisi kuchagua pointi mbili zifuatazo kwenye mstari uliopewa:\((2, 0)\),,,\((0, 1)\)\((4, −1)\),\((6, −2)\)\((−4, 3)\)\((−6, 4)\), na kadhalika...
Mteremko ni sawa kwa pointi yoyote mbili\(P\) na\(Q\) kwenye mstari. Chagua uhakika\(P_1\) kuwa\((0, 1)\) na uhakika\(Q_1\) kuwa\((2, 0)\). Kuanzia katika hatua\(P_1\), kufikia hatua\(Q_1\) kwa kwanza mbio mraba\(2\) gridi ya taifa na haki, ambayo ina maana kwamba\(\text{run} = 2\). Sasa, kuwasili kwa uhakika\(Q_1\) kuhesabu chini\(1\) gridi ya taifa mraba. Kumbuka, kwamba\(\text{rise} = -1\) ambayo ina maana ya hoja chini\(1\) kitengo kama inavyoonekana katika takwimu hapa chini.
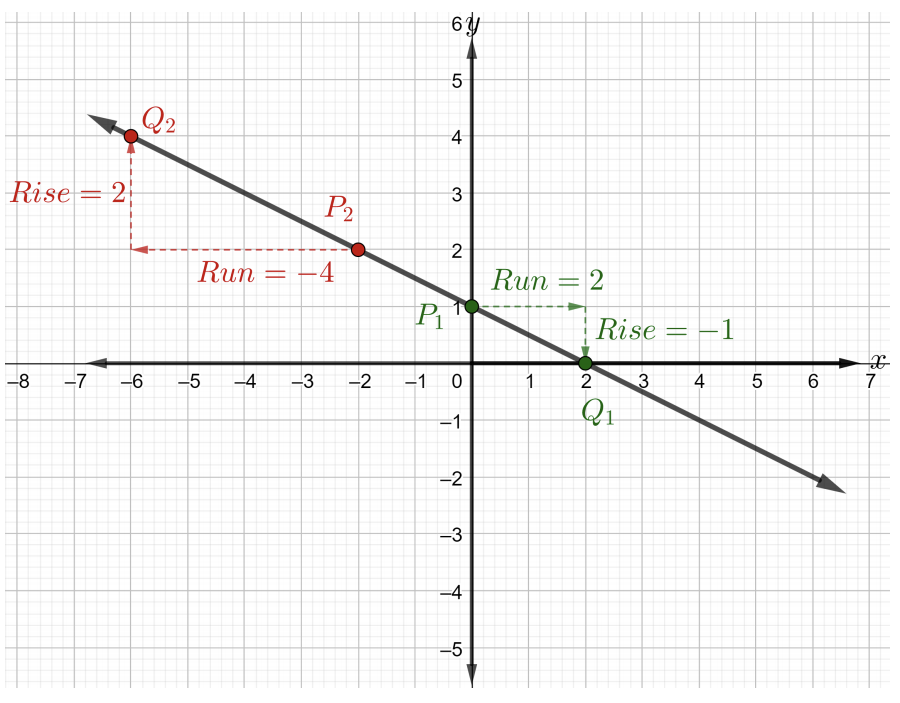
\(\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{−1}{2} &\text{rise = \(-1\)na kukimbia =\(2\)}\ mwisho {array}\)
Kwa hiyo, mteremko wa mstari katika takwimu hapo juu ni\(m = −\dfrac{1}{2}\).
Sasa, chagua uhakika\(P_2\) kuwa\((-2, 2)\) na uhakika\(Q_2\) kuwa\((-6, 4)\) kama inavyoonekana katika takwimu hapo juu. Kuanzia saa pointi\(P_2\), kufikia hatua\(Q_2\) kwa kwanza mbio mraba\(4\) gridi upande wa kushoto, ambayo ina maana kwamba\(\text{run} = -4\). Sasa, kufika kwa uhakika\(Q_2\) kuhesabu mraba\(2\) gridi ya juu. Hivyo, the\(\text{rise} = 2\). Mteremko ni\(m = \dfrac{2}{−4} = −\dfrac{1}{2}\). Angalia, mteremko ni sawa bila kujali\(2\) pointi ambazo tunazingatia kwenye mstari uliopewa.
Pata mteremko wa mstari unaopita\((3, 2)\) na\((4, 4)\) kutumia formula ya mteremko. Grafu mstari unaopita kupitia pointi zilizopewa.
Kumbuka: Utaratibu wa pointi zimeandikwa hazitafanya tofauti katika mteremko wa fomu ya mstari kwa muda mrefu kama kuna msimamo.
Suluhisho
Hebu\((x_1, y_1) = (3, 2)\) na\((x_2, y_2) = (4, 4)\) kisha,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{4 − 2}{4 − 3} & \\ &= \dfrac{2}{1} &\text{rise \(= 2\)na kukimbia\(= 1\)}\\ &= 2 &\ mwisho {safu}\)
Kwa hiyo, mteremko wa mstari unaopita kupitia pointi\((3, 2)\) na\((4, 4)\) ni\(m = 2\). Mstari unaopita kupitia pointi zilizopewa ni kama inavyoonekana katika takwimu hapa chini.
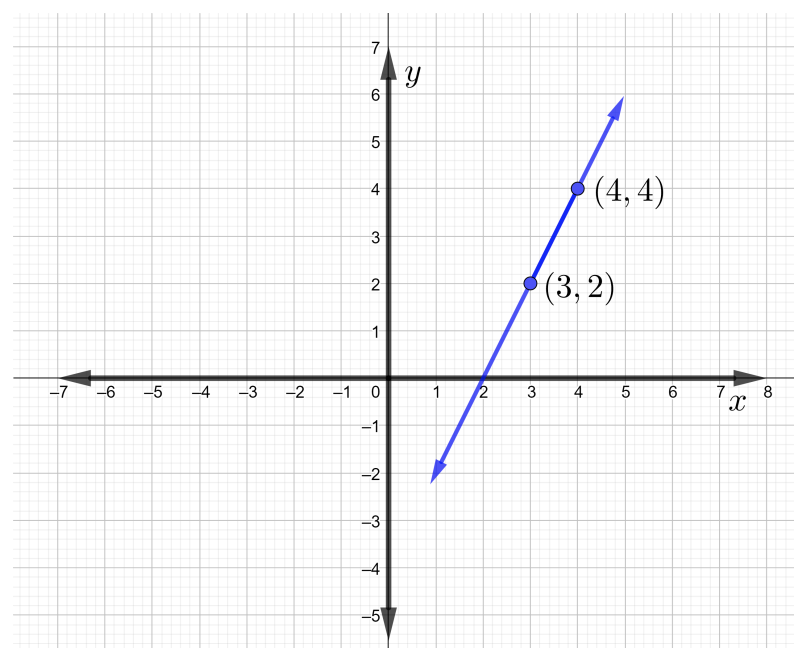
Angalia kwamba wakati mstari unapoinuka kutoka kushoto kwenda kulia, mstari una mteremko mzuri.
Pata mteremko wa mstari unaopita kupitia pointi\((−1, 2)\) na\((3, −4)\). Panda pointi na grafu mstari.
Suluhisho
Hebu\((x_1, y_1) = (-1, 2)\) na\((x_2, y_2) = (3, -4)\) kisha,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{-4 − 2}{3 − (-1)} & \\ &= \dfrac{-6}{4} &\text{Simplify} \\ &= -\dfrac{3}{2} & \end{array}\)
Sasa, ili kuchora mstari kupitia pointi zilizotolewa, kwanza njama pointi mbili, kisha futa mstari wa moja kwa moja kupitia kwao, kama inavyoonekana kwenye Mchoro hapa chini.
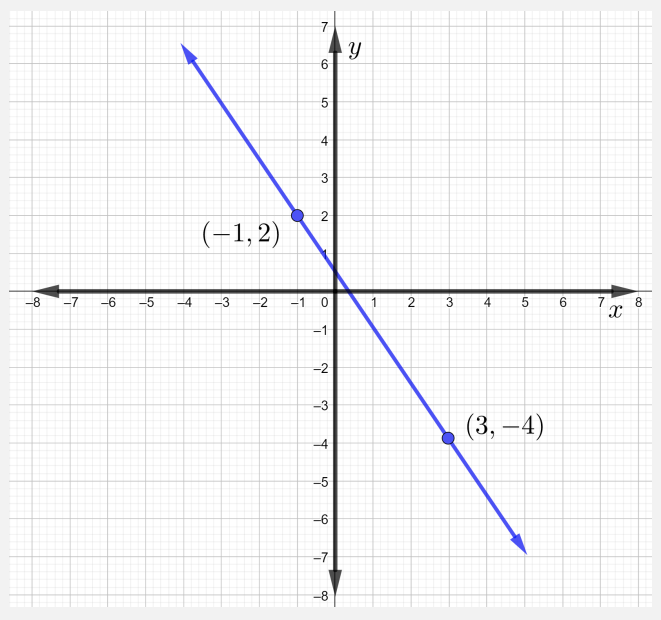
Angalia kwamba wakati mstari unapoanguka kutoka kushoto kwenda kulia, mstari una mteremko hasi.
Kupata mteremko wa kila mstari katika grafu katika Matatizo\(1\) kupitia\(4\)
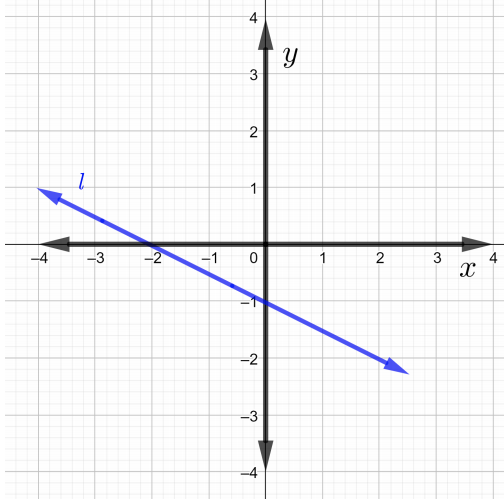
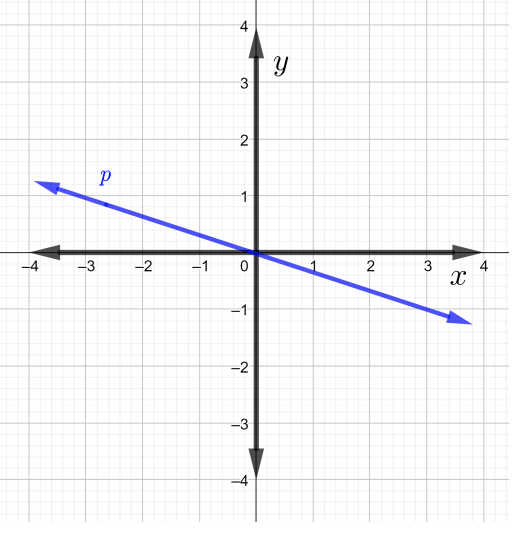
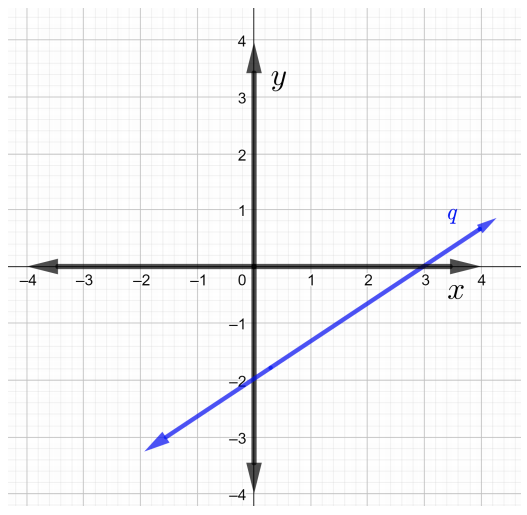
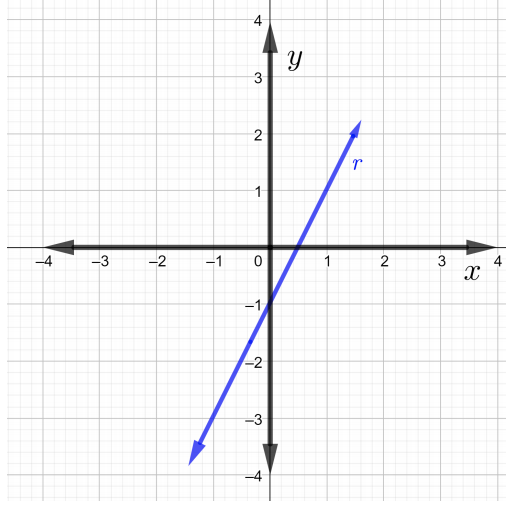
Pata mteremko wa mstari unaopita kupitia pointi zilizopewa katika Matatizo\(5\) kupitia\(7\).
- \((−3, 5)\)na\((4, −5)\)
- \((2, 5)\)na\((0, −1)\)
- \((4, 1)\)na\((0, 0)\)


