4.6: Kazi nyingi
- Page ID
- 164646
Kazi ya Polynomial ni kazi ambayo inaweza kuandikwa kwa fomu ya jumla:
\(f(x) = a_n x^n + a_{n−1} x^{n−1 }+ ... + a_1x + a_0\)
\(n\)kwa integer isiyo ya hasi, inayoitwa shahada ya polynomial. Coefficients\(a_0\),\(a_1\)\(\ldots\), na ni namba halisi na mgawo wa kuongoza an\(a_n \neq 0\). Uwanja wa Kazi ya Polynomial ni\((−\infty , \infty )\). Grafu ya kazi ya polynomial ya shahada\(n\) inaweza kuingiliana na x-axis\(n\) mara nyingi. Hizi ni mizizi ya kazi ya polynomial.
Hakuna mifano au kazi za nyumbani katika sehemu hii.
Kazi za Quadratic
\(f(x) = ax^2 + bx + c\)wapi\(a\neq 0\)
ni Kazi ya Quadratic katika fomu ya kawaida, na grafu yake ni parabola. Wakati mgawo wa kuongoza\(a\), ni chanya, grafu ya Kazi ya Quadratic inafungua juu. Wakati mgawo wa kuongoza\(a\),, ni hasi, grafu ya Kazi ya Quadratic inafungua chini.
Mchoro grafu ya mfumo\(f(x) = −x^2 + 5x + 3\) wa kuratibu mstatili. Pata vertex, x-intercept (s) na y-intercept algebraically.
Suluhisho
Pata vertex kwa kuhesabu\(\left(\dfrac{-b}{2 a}, f\left(\dfrac{-b}{2 a}\right)\right)\) na\(a = −1\),\(b = 5\) na\(c = 3\).
\ (\ kuanza {iliyokaa}
\ kushoto (\ dfrac {-b} {2 a}, f\ kushoto (\ dfrac {-b} {2 a}\ haki)\ haki) &=&\ maandishi {Pata kipeo cha parabola}\
\ dfrac {-5} {2 (-1)} &=\
\ dfrac {5} {2} &=2.5 &\ Nakala {Kurahisisha}\
\ dfrac {-5} {2 (-1)} &=2.5\\
f (2.5) &=- (2.5) ^ {2} +5 (2.5) +3=9.25=&f\ kushoto (\ dfrac {-b} {2 a}\ kulia) =9.25\\ kushoto (\ dfrac {-b} {2 a}, f\ kushoto (\ dfrac {-b} {2 a}\ haki) & =( 2.5,9.25) &&\ maandishi {Vertex ya parabola}
\ mwisho {iliyokaa}\)
Ili kupata intercepts:
\ (\ kuanza {iliyokaa} 0 & = -x^ {2} +5 x+3 &\ maandishi {x-intercept, kuweka} f (x) =0\\ 0 & = -x^ {2} +5 x+3 &\ maandishi {Tumia Mfumo wa Quadratic kutatua equation hii (haiwezi kuhesabiwa). Hebu} a=-1, b = 5, c = 3\\ x&=\ dfrac {-5\ pm\ sqt {(5) ^ {2} -4 (-1) (3)} {2 (-1)} &\ maandishi {Mfumo wa Quadratic}\ x&=\ dfrac {-5\ pm\ sqrt {37
}} {-2} &\ maandishi {Kurahisisha}\\ x&=\ xrac {-5\ pm\ sqrt {37}} &\ Nakala {Kurahisisha}\\
x&&=-0.54\ maandishi {au} x=5.54 &&\ maandishi {Kazi hii ya quadratic ina mizizi miwili (x-intercepts). }\\ f (0) &=-0^ {2} +5 (0) +3 &&\ maandishi {y-kukatiza, kuweka} x = 0\\ f (0) &=3 &&\ maandishi {y-intercept}\ mwisho {iliyokaa}\)
Grafu jozi nne zilizoamriwa, na uhesabu jozi zilizoamriwa zaidi ikiwa inahitajika:\((2.5, 9.25)\)\((−.54, 0)\),\((5.54, 0)\),,\((0, 3)\).

- \(f(x) = 2x ^2 − 5x − 5\)
- \(f(x) = 0.5x ^2 − 6x + 21\)
- \(f(x) = −4x ^2 − 8x − 3\)
- \(f(x) = −4x^ 2 + 16x − 15\)
- \(f(x) = x^ 2 − 8x + 12\)
- \(f(x) = −7x^ 2 + 100x − 10\)
Kazi za Cubic na za Juu
Kazi ya Cubic ni kazi ya shahada ya tatu ya polynomial ambayo inaweza kuandikwa kwa fomu ya jumla:
\(f(x) = a_3x^ 3 + a_2x^2 + a_1x + a_0\)
na 3 kama shahada ya kazi za ujazo. Coefficients\(a_0\),\(a_1\),\(a_2\),\(a_3\) ni namba halisi na mgawo wa kuongoza\(a_3 \neq 0\). Kikoa cha kazi ya ujazo ni\((−\infty , \infty )\).
Factor kama inawezekana na grafu kazi kwa kujenga meza ya ufumbuzi:
\(f(x) = x^3 − 4x^2 + 6x − 1\)
Suluhisho
Polynomial hii ni ya shahada ya 3, na ni vigumu kuzingatia. Unda meza ya ufumbuzi wa grafu.

| Jedwali la Solutions kwa\(f(x) = x^3 − 4x^2 + 6x − 1\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^3 − 4(−2)^2 + 6(−2) − 1 = −37\) |
| -1 | \(f(−1) = (−1)^3 − 4(−1)^2 + 6(−1) − 1 = −12\) |
| 0 | \(f(0) = (0)^3 − 4(0)^2 + 6(0) − 1 = −1\) |
| 1 | \(f(1) = (1)^3 − 4(1)^2 + 6(1) − 1 = 2\) |
| 2 | \(f(2) = (2)^3 − 4(2)^2 + 6(2) − 1 = 3\) |
Factor kama inawezekana na grafu kazi kwa kujenga meza ya ufumbuzi:
\(g(x)=x^4-16\)
Suluhisho
Polynomial hii ni ya shahada ya 4, na kwa sababu ni tofauti ya mraba, inaweza kuhesabiwa katika bidhaa ya binomials ili kupata zero za polynomial. Unda meza ya ufumbuzi wa grafu.
\(\begin{aligned} g(x)&=\left(x^{2}-4\right)\left(x^{2}+4\right) && \text{Factoring into the sum and difference of binomials.} \\ g(x)&=(x-2)(x+2)\left(x^{2}+4\right) && \text{Further factoring. Set each binomial equal to zero to find the real number zeroes of the polynomial.} \\ x-2&=0, x=2 && \text{The first real number zero of the polynomial, }(2,0) \\ x+2&=0, x=-2 &&\text{The second real number zero of the polynomial, } (2,0) \\ x^{2}+4&=0, x^{2}=-4 && \text{The third binomial factor does not produce real number zeroes, } \\ & &&\text{because no number squared can result in a negative value.} \end{aligned}\)
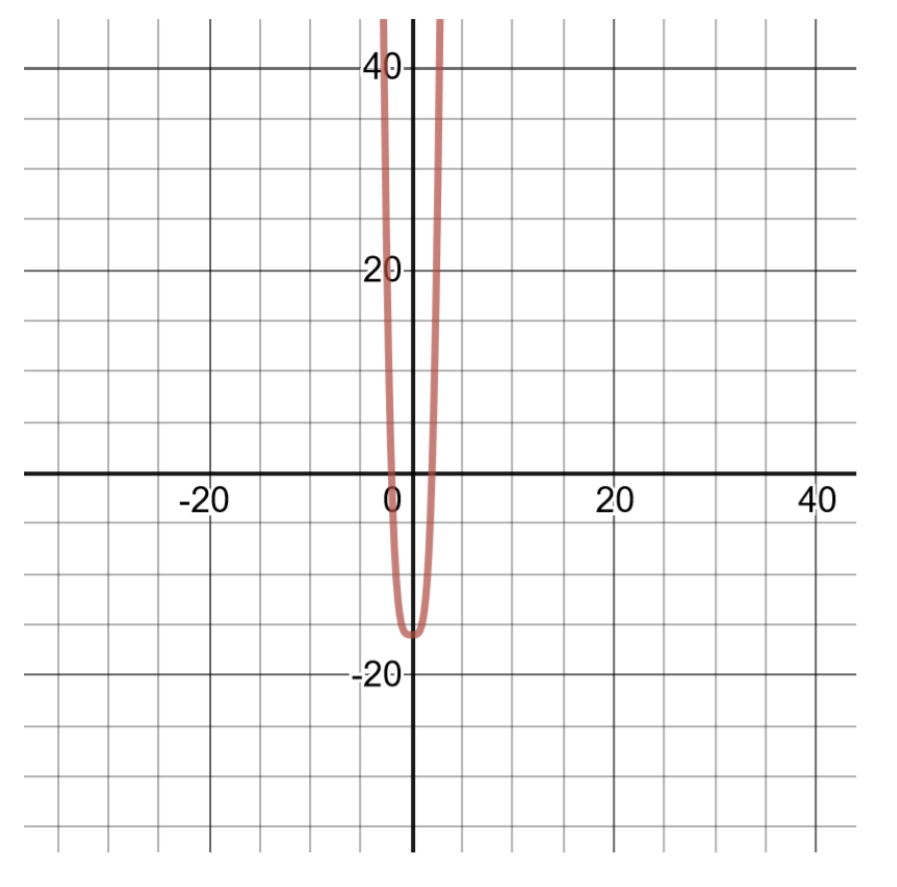
| Jedwali la Solutions kwa\(g(x)=x^4-16\) | |
| \(x\) | \(g(x)\) |
| -2 | \(g(−2) = (−2)^4 − 16 = 16 − 16 = 0\) |
| -1 | \(g(−1) = (−1)^4 − 16 = 1 − 16 = −15\) |
| 0 | \(g(0) = (0)^4 − 16 = 0 − 16 = −16\) |
| 1 | \(g(1) = g(1) = (1)^4 − 16 = 1 − 16 = −15\) |
| 2 | \(g(2) = g(2) = (2)^4 − 16 = 16 − 16 = 0\) |
Factor kama inawezekana na grafu kazi kwa kujenga meza ya ufumbuzi:
\(f(x) = x ^6 − 5x ^2 + 3\)
Suluhisho
Polynomial hii ni ya shahada ya 6, na ni vigumu kuzingatia. Unda meza ya ufumbuzi wa grafu.
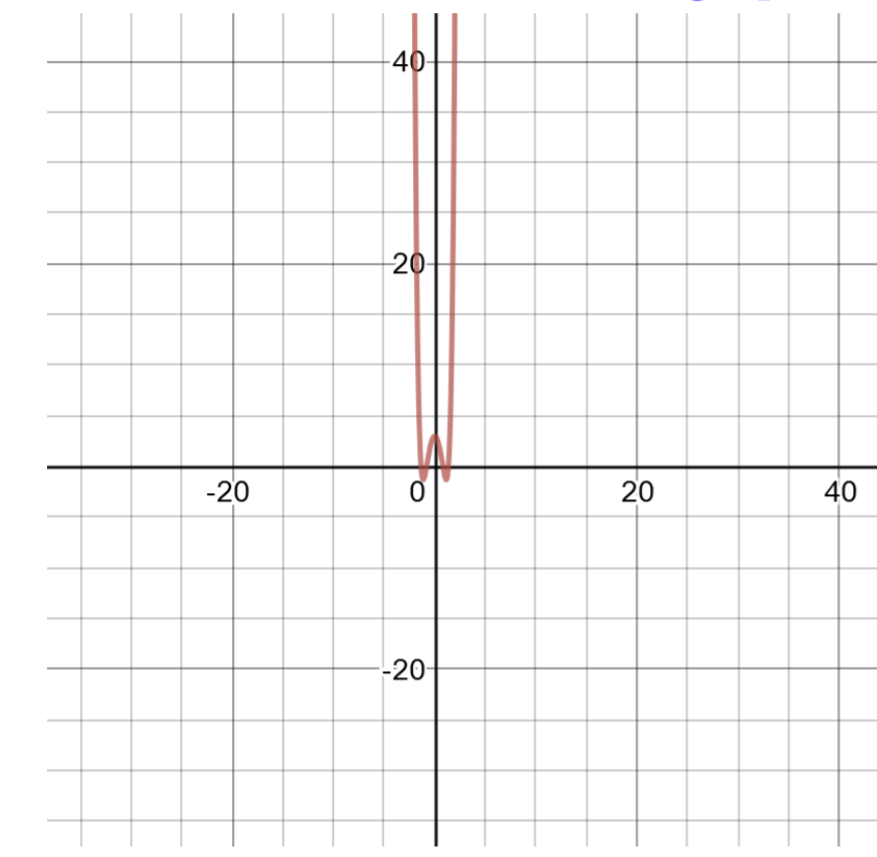
| Jedwali la Solutions kwa\(f(x) = x ^6 − 5x ^2 + 3\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^6 − 5(−2)^2 + 3 = 47\) |
| -1 | \(f(−1) = (−1)^6 − 5(−1)^2 + 3 = −1\) |
| 0 | \(f(0) = (0)^6 − 5(0)^2 + 3 = 3\) |
| 1 | \(f(1) = (1)^6 − 5(1)^2 + 3 = −1\) |
| 2 | \(f(2) = (2)^6 − 5(2)^2 + 3 = 47\) |
- \(f(x) = x^3 − 27\)
- \(g(x) = 81x ^4 − 16\)
- \(h(x) = 2x ^5 − 4x ^2 − 6x + 3\)
- \(f(x) = 5x ^6 − 6x ^4 + 5\)
Kazi za busara
Kazi ya busara ni kazi ambayo inaweza kuandikwa kama quotient ya polynomials.
\(f(x) = \dfrac{P (x) }{Q(x) }\),\(Q(x) \neq 0\)
wapi\(P(x)\) na\(Q(x)\) ni polynomials katika variable moja\(x\). Kikoa ni seti ya namba zote halisi kama hizo\(Q(x) \neq 0\).
Kwa kazi,\(f(x) = \dfrac{9 }{x − 3}\):
- Graph kazi
- Tathmini kazi kwa\(x = 0\) na\(x = 2\)
Suluhisho
Jihadharini na uwanja wa kazi hii. Idara na sifuri haijulikani, hivyo namba (s) ambayo itafanya denominator 0 lazima iondokewe kwenye kikoa.
Katika tatizo hili,\(x − 3\) ni katika denominator ya kazi. Kuweka\(x − 3 = 0\) na kutatua kwa\(x\). Ikiwa\(x = 3\) mgawanyiko haujafafanuliwa, hivyo usiondoe namba 3 kutoka kwenye uwanja wa kazi. Fikiria kama daima kuanzia na namba zote halisi\((−\infty , \infty )\) na kisha kuondoa maadili ambayo yatasababisha mgawanyiko usiojulikana.
Kikoa cha kazi hii ni\((−\infty , 3) \cup (3, \infty )\).
Kazi za busara mara nyingi zitakuwa na asymptotes, mstari unaoendelea unakaribia pembe iliyotolewa lakini haukutana nayo kwa umbali wowote wa mwisho. Utajifunza kuhusu asymptotes katika sehemu ya Sketching ya Curve ya Math 162.
Grafu ya kazi hii inaweza kupatikana kwa kufanya meza ya ufumbuzi:

| Jedwali la Solutions kwa\(f(x) = \dfrac{9 }{x − 3}\) | Domain:\((−\infty , 3) \cup (3, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | \(-\dfrac{9}{7}\) |
| -3 | \(-\dfrac{3}{2}\) |
| -2 | \(-\dfrac{9}{5}\) |
| -1 | \(-\dfrac{9}{4}\) |
| 0 | \(-3\) |
| 1 | \(-\dfrac{9}{2}\) |
| 2 | \(-9\) |
Kwa kazi,\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\)
- Graph kazi
- Tathmini kazi kwa\(x = −1\) na\(x = 3\)
Suluhisho
Jihadharini na uwanja wa kazi hii. Idara na sifuri haijulikani, hivyo namba (s) ambayo itafanya denominator 0 lazima iondokewe kwenye kikoa.
Katika tatizo hili,\(x^2 − 3x − 4\) ni katika denominator ya kazi. Fanya kujieleza kwa quadratic kupata\((x − 4)(x + 1)\) na kuweka kila sababu sawa na sifuri na kutatua kwa\(x\):\(x − 4 = 0\), hivyo\(x = 4\);\(x + 1 = 0\), hivyo\(x = −1\). Ikiwa\(x = 4\) au\(x = −1\), mgawanyiko haujafafanuliwa, hivyo usiondoe namba 4 na -1 kutoka kwenye uwanja wa kazi. Fikiria kama daima kuanzia na namba zote halisi\((−\infty , \infty )\) na kisha kuondoa maadili ambayo yatasababisha mgawanyiko usiojulikana.
Kikoa cha kazi hii ni\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\). Grafu ya kazi hii inaweza kupatikana kwa kufanya meza ya ufumbuzi:
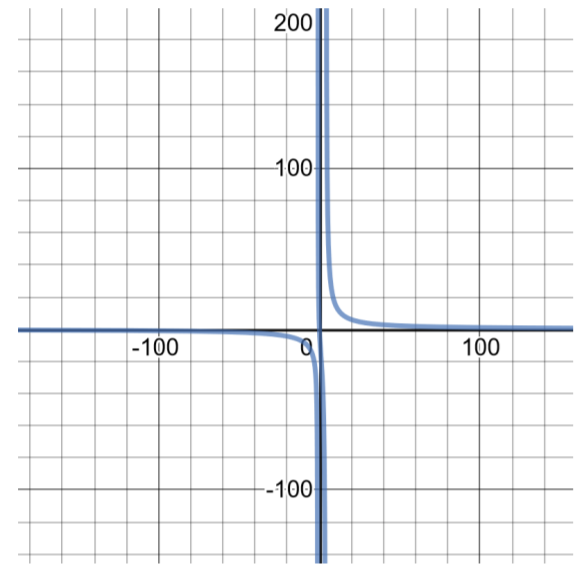
| Jedwali la Solutions kwa\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\) | Domain:\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | -16.667 |
| -3 | -21.429 |
| -2 | -33.333 |
| -1 | haijafafanuliwa |
| 0 | 0 |
| 1 | -16.667 |
| 2 | -33.333 |
| 3 | -75 |
| 4 | haijafafanuliwa |
- \(f(x) = \dfrac{3x + 6 }{x − 1}\)
- \(f(x) = \dfrac{9 }{x^2 − 9}\)
- \(f(x) = \dfrac{x^ 2 − 4 }{x^2 − 4x}\)


