3.5: Muda Notation na Infinity
- Page ID
- 164579
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Je, ni infinity? Infinity si idadi halisi. Infinity ni kubwa kuliko idadi yoyote ambayo inaweza kufikiria. Ni wazo la kuwa na mipaka isiyo na mipaka. Mstari ni mfano wa kutokuwa na mipaka. Kwa mfano mstari wa namba una mishale mwishoni ili kuwakilisha wazo hili la kuwa na mipaka. Ishara inayotumiwa kuwakilisha infinity ni\(\infty\). Kwenye upande wa kushoto wa mstari wa namba ni\(−\infty\) na upande wa kulia wa mstari wa nambari ni\(\infty\) kuelezea tabia isiyo na mipaka ya mstari wa namba.
| Muda Nukuu | Nambari ya mstari |
| a)\((12,\infty)\) |
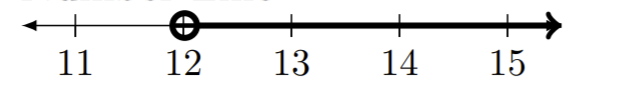
|
| b)\([-5,\infty)\) |
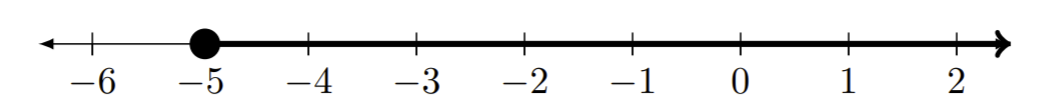
|
| c)\((−\infty,4)\) |

|
| d)\((−\infty,0]\) |
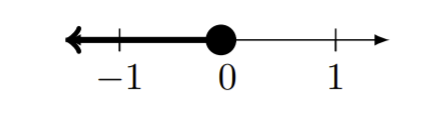
|
| e)\((−\infty,\infty)\) |
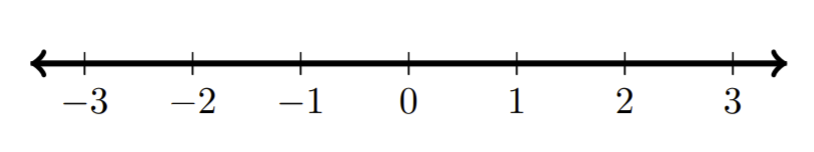
|
Kumbuka: Kwa kuwa\(\infty\) si idadi halisi, inahitajika kutumia mabano (,). \(\infty\)haiwezi kuingizwa katika kipindi.
Chora mstari wa nambari unaofanana na vipindi vifuatavyo.
- \((−\infty,5)\)
- \([-5,\infty)\)
- \((−\infty,\infty)\)
- \((-3,\infty)\)
- \((−\infty,-2]\)


