1.4: Medições
- Page ID
- 185232
‣
- Explique o processo de medição e descreva as três partes básicas de uma quantidade.
- Descreva as propriedades e unidades de comprimento, massa, volume, densidade, temperatura e tempo.
- Reconheça os prefixos de unidades comuns e use-os para descrever a magnitude de uma medição.
- Descreva e calcule a densidade de uma substância.
- Execute cálculos e conversões de unidades básicas no sistema métrico e em outros sistemas de unidades.
As medições fornecem as informações macroscópicas que são a base da maioria das hipóteses, teorias e leis que descrevem o comportamento da matéria e da energia nos domínios macroscópico e microscópico da química. Cada medição fornece três tipos de informações: o tamanho ou a magnitude da medição (um número); um padrão de comparação para a medição (uma unidade); e uma indicação da incerteza da medição. Embora o número e a unidade sejam representados explicitamente quando uma quantidade é escrita, a incerteza é um aspecto do resultado da medição que é representado de forma mais implícita e será discutido posteriormente.
O número na medição pode ser representado de diferentes maneiras, incluindo a forma decimal e a notação científica. Por exemplo, o peso máximo de decolagem de um avião Boeing 777-200ER é de 298.000 kg, o que também pode ser escrito como 2,98\(\times\) 10 5 kg. A massa média do mosquito é de cerca de 0,0000025 kg, o que pode ser escrito como 2,5\(\times\) 10 −6 kg.
Unidades, como litros, libras e centímetros, são padrões de comparação para medições. Quando compramos uma garrafa de 2 litros de refrigerante, esperamos que o volume da bebida tenha sido medido, então é duas vezes maior do que o volume que todos concordam em ser de 1 litro. A carne usada para preparar um hambúrguer de 0,25 libras é medida para pesar um quarto até 1 libra. Sem unidades, um número pode ser insignificante, confuso ou possivelmente fatal. Suponha que um médico prescreva fenobarbital para controlar as convulsões de um paciente e indique uma dosagem de “100” sem especificar unidades. Isso não só confundirá o profissional médico que administra a dose, mas as consequências podem ser terríveis: 100 mg administrados três vezes ao dia podem ser eficazes como anticonvulsivantes, mas uma dose única de 100 g é mais de 10 vezes a quantidade letal.
Normalmente relatamos os resultados das medições científicas em unidades SI, uma versão atualizada do sistema métrico, usando as unidades listadas na Tabela\(\PageIndex{1}\). Outras unidades podem ser derivadas dessas unidades básicas. Os padrões para essas unidades são fixados por acordo internacional e são chamados de Sistema Internacional de Unidades ou Unidades SI (do francês Le Système International d'Unités). As unidades SI são usadas pelo Instituto Nacional de Padrões e Tecnologia dos Estados Unidos (NIST) desde 1964.
| Propriedade medida | Nome da unidade | Símbolo da unidade |
|---|---|---|
| comprimento | contador | m |
| massa | quilograma | kg |
| horas | segundo | s |
| temperatura | kelvin | K |
| corrente elétrica | ampere | UMA |
| quantidade de substância | toupeira | toupeira |
| intensidade luminosa | candela | cd |
Às vezes, usamos unidades que são frações ou múltiplos de uma unidade base. O sorvete é vendido em litros (uma unidade base familiar que não é SI), litros (0,5 litro) ou galões (4 litros). Também usamos frações ou múltiplos de unidades no sistema SI, mas essas frações ou múltiplos são sempre potências de 10. As unidades SI fracionárias ou múltiplas são nomeadas usando um prefixo e o nome da unidade base. Por exemplo, um comprimento de 1000 metros também é chamado de quilômetro porque o prefixo quilo significa “mil”, que em notação científica é 10 3 (1 quilômetro = 1000 m = 10 3 m). Os prefixos usados e os poderes aos quais 10 são aumentados estão listados na Tabela\(\PageIndex{2}\).
NG, igual a 4 vezes dez elevado a menos 9, ou 0,0000004 g. O prefixo micro tem a letra grega mu como símbolo e um fator de 10 elevado a menos sexta potência. Portanto, 1 microlitro, ou mu L, é igual a um vezes dez elevado a menos 6 ou 0,000001 L. O prefixo milli tem um M minúsculo como símbolo e um fator de 10 elevado à terceira potência negativa. Portanto, 2 milimoles, ou M mol, são iguais a duas vezes dez elevado a menos 3 ou 0,002 mol. O prefixo centi tem um C minúsculo como símbolo e um fator de 10 elevado à segunda potência negativa. Portanto, 7 centímetros, ou C M, são iguais a sete vezes dez elevado a menos 2 metros ou 0,07 M O L. O prefixo deci tem um D minúsculo como símbolo e um fator de 10 elevado à primeira potência negativa. Portanto, 1 decilitro, ou D minúsculo L maiúsculo, é igual a um vezes dez elevado a menos 1 metro ou 0,1 L. O prefixo quilo tem um K minúsculo como símbolo e um fator de 10 elevado à terceira potência. Portanto, 1 quilômetro, ou K M, é igual a um vezes dez elevado ao terceiro metro ou 1000 M. O prefixo mega tem um M maiúsculo como símbolo e um fator de 10 elevado à sexta potência. Portanto, 3 megahertz, ou M H Z, são iguais a três vezes 10 elevado ao sexto hertz, ou 3000000 H Z. O prefixo giga tem um G maiúsculo como símbolo e um fator de 10 elevado à nona potência. Portanto, 8 gigaanos, ou G Y R, são iguais a oito vezes 10 ao nono ano, ou 800000000 G Y R. O prefixo tera tem um T maiúsculo como símbolo e um fator de 10 elevado à décima segunda potência. Portanto, 5 terawatts, ou T W, são iguais a cinco vezes 10 elevado a doze watts, ou 5000000000000 W.” data-quail-id="64" data-mt-width="1076">
| Prefixo | Símbolo | Fator | Exemplo |
|---|---|---|---|
| femto | f | 10 −15 | 1 femtosec one (fs) = 1\(\times\) 10 −15 s (0,0000000000001 s) |
| pico | p | 10 −12 | 1 picômetro (pm) = 1\(\times\) 10 −12 m (0,000000000001 m) |
| nano | n | 10 −9 | 4 nanogramas (ng) = 4\(\times\) 10 −9 g (0,0000004 g) |
| micro | µ | 10 −6 | 1 microlitro (μL) = 1\(\times\) 10 −6 L (0,000001 L) |
| mili | m | 10 −3 | 2 milimoles (mmol) = 2\(\times\) 10 −3 mol (0,002 mol) |
| centi | c | 10 −2 | 7 centímetros (cm) = 7\(\times\) 10 −2 m (0,07 m) |
| deci | d | 10 −1 | 1 decilitro (dL) = 1\(\times\) 10 −1 L (0,1 L) |
| quilo | k | 10 3 | 1 quilômetro (km) = 1\(\times\) 10 3 m (1000 m) |
| mega | M | 10 6 | 3 megahertz (MHz) = 3\(\times\) 10 6 Hz (3.000.000 Hz) |
| giga | G | 10 9 | 8 gigaanos (Gyr) = 8\(\times\) 10 9 anos (8.000.000.000 Gyr) |
| tera | T | 10 12 | 5 terawatts (TW) = 5\(\times\) 10 12 W (5.000.000.000.000 W) |
Unidades base SI
As unidades iniciais do sistema métrico, que eventualmente evoluíram para o sistema SI, foram estabelecidas na França durante a Revolução Francesa. Os padrões originais para o medidor e o quilograma foram adotados lá em 1799 e, eventualmente, por outros países. Esta seção apresenta quatro das unidades base SI comumente usadas em química. Outras unidades SI serão introduzidas nos capítulos subsequentes.
Comprimento
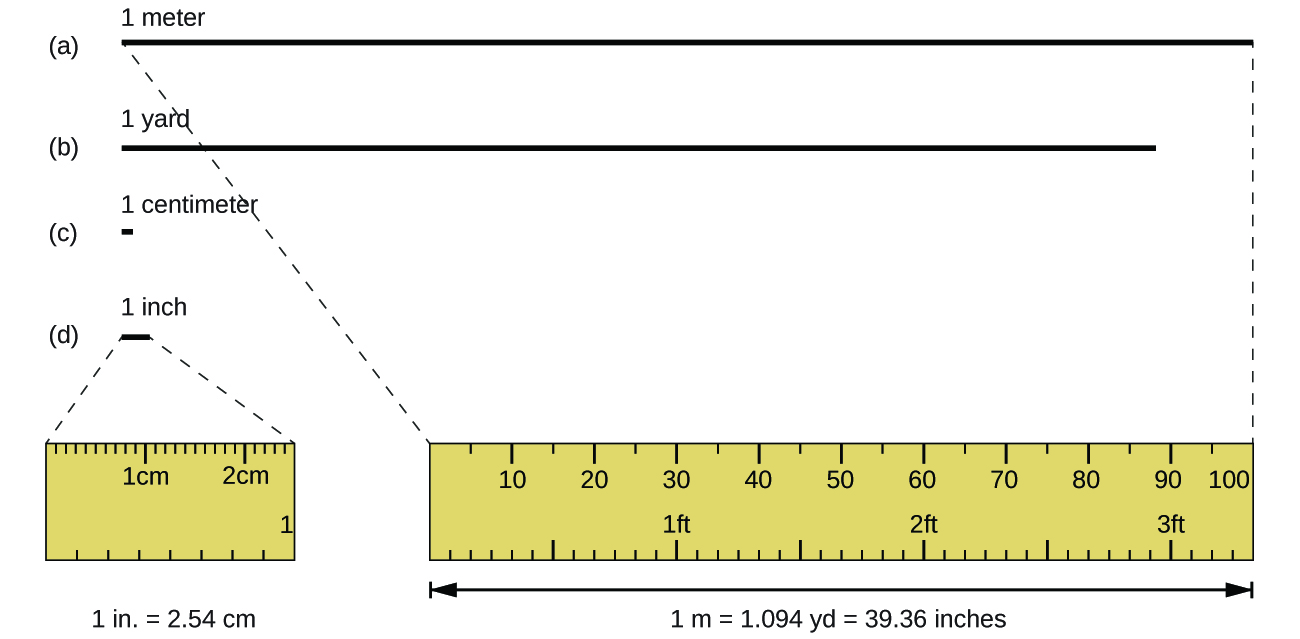
A unidade padrão de comprimento nos sistemas métrico SI e original é o medidor (m). Um metro foi originalmente especificado como 1/10.000.000 da distância do Pólo Norte até o equador. Agora é definido como a distância que a luz no vácuo percorre em 1/299.792.458 de segundo. Um metro é cerca de 3 polegadas mais longo do que uma jarda (Figura\(\PageIndex{1}\)); um metro tem cerca de 39,37 polegadas ou 1.094 jardas. Distâncias maiores são frequentemente relatadas em quilômetros (1 km = 1000 m = 10 3 m), enquanto distâncias mais curtas podem ser relatadas em centímetros (1 cm = 0,01 m = 10 −2 m) ou milímetros (1 mm = 0,001 m = 10 −3 m).
Missa
A unidade de massa padrão no sistema SI é o quilograma (kg). Um quilograma foi originalmente definido como a massa de um litro de água (um cubo de água com um comprimento de borda de exatamente 0,1 metro). Agora é definido por um certo cilindro de liga de platina-irídio, que é mantido na França (Figura 1.4.2). Diz-se que qualquer objeto com a mesma massa desse cilindro tem uma massa de 1 kg. Um quilo equivale a cerca de 2,2 libras. O grama (g) é exatamente igual a 1/1000 da massa do quilograma (10 −3 kg).

Temperatura
A temperatura é uma propriedade intensiva. A unidade de temperatura SI é o kelvin (K). A convenção da IUPAC é usar kelvin (tudo em minúsculas) para a palavra, K (maiúscula) para o símbolo da unidade e nem a palavra “grau” nem o símbolo de grau (°). O grau Celsius (°C) também é permitido no sistema SI, com a palavra “grau” e o símbolo de grau usados para medições em graus Celsius. Os graus Celsius têm a mesma magnitude que os de Kelvin, mas as duas escalas colocam seus zeros em lugares diferentes. A água congela a 273,15 K (0° C) e ferve a 373,15 K (100° C) por definição, e a temperatura normal do corpo humano é de aproximadamente 310 K (37° C). A conversão entre essas duas unidades e a escala Fahrenheit será discutida posteriormente neste capítulo.
Horário
A unidade base de tempo do SI é o (s) segundo (s). Intervalos de tempo pequenos e grandes podem ser expressos com os prefixos apropriados; por exemplo, 3 microssegundos = 0,000003 s = 3\(\times\) 10 −6 e 5 megassegundos = 5.000.000 s = 5\(\times\) 10 6 s. Como alternativa, horas, dias e anos podem ser usados.
Unidades SI derivadas
Podemos derivar muitas unidades das sete unidades base SI. Por exemplo, podemos usar a unidade base de comprimento para definir uma unidade de volume e as unidades base de massa e comprimento para definir uma unidade de densidade.
Volume
O volume é a medida da quantidade de espaço ocupado por um objeto. A unidade de volume SI padrão é definida pela unidade base de comprimento (Figura\(\PageIndex{3}\)). O volume padrão é um metro cúbico (m 3), um cubo com um comprimento de borda de exatamente um metro. Para dispensar um metro cúbico de água, poderíamos construir uma caixa cúbica com comprimentos de borda de exatamente um metro. Essa caixa teria um metro cúbico de água ou qualquer outra substância.
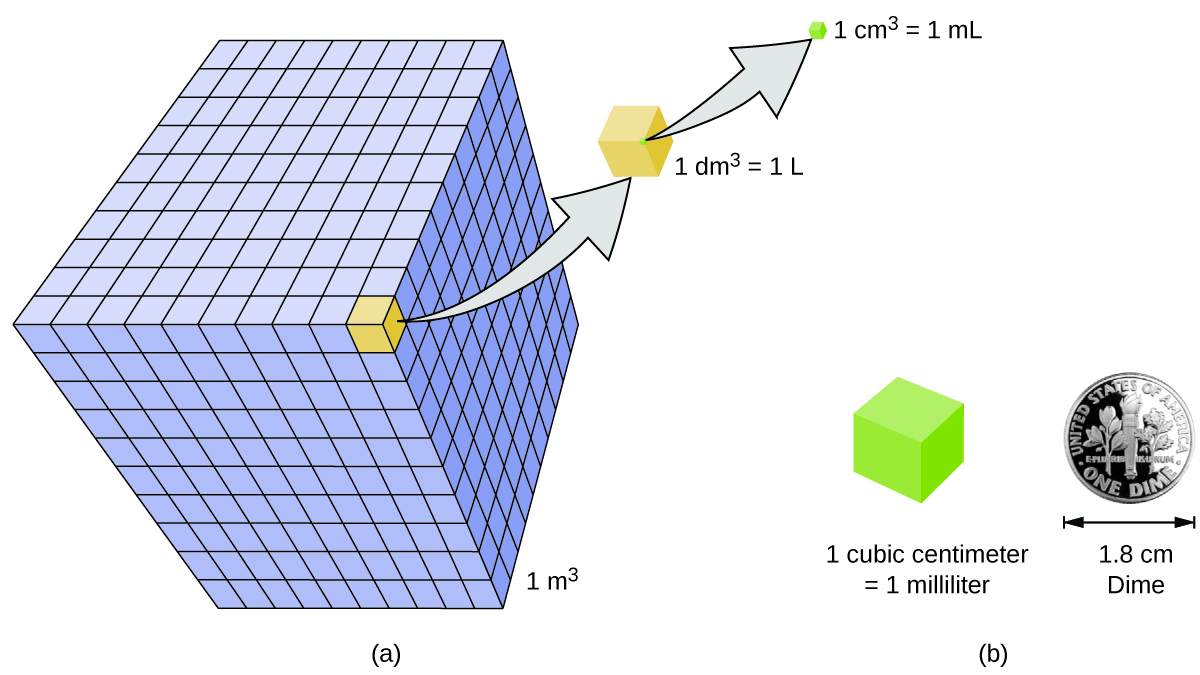
Uma unidade de volume mais usada é derivada do decímetro (0,1 m ou 10 cm). Um cubo com comprimentos de borda de exatamente um decímetro contém um volume de um decímetro cúbico (dm 3). Um litro (L) é o nome mais comum para o decímetro cúbico. Um litro equivale a cerca de 1,06 litros. Um centímetro cúbico (cm 3) é o volume de um cubo com um comprimento de borda de exatamente um centímetro. A abreviatura cc (para c ubic c entímetro) é frequentemente usada por profissionais de saúde. Um centímetro cúbico também é chamado de mililitro (mL) e é 1/1000 de um litro.
Densidade
Usamos a massa e o volume de uma substância para determinar sua densidade. Assim, as unidades de densidade são definidas pelas unidades básicas de massa e comprimento.
A densidade de uma substância é a razão entre a massa de uma amostra da substância e seu volume. A unidade SI para densidade é o quilograma por metro cúbico (kg/m 3). Em muitas situações, no entanto, essa é uma unidade inconveniente, e costumamos usar gramas por centímetro cúbico (g/cm 3) para as densidades de sólidos e líquidos e gramas por litro (g/L) para gases. Embora haja exceções, a maioria dos líquidos e sólidos tem densidades que variam de cerca de 0,7 g/cm 3 (a densidade da gasolina) a 19 g/cm 3 (a densidade do ouro). A densidade do ar é de cerca de 1,2 g/L. A tabela\(\PageIndex{3}\) mostra as densidades de algumas substâncias comuns.
| Sólidos | Líquidos | Gases (a 25 °C e 1 atm) |
|---|---|---|
| gelo (a 0 °C) 0,92 g/cm 3 | água 1,0 g/cm 3 | ar seco 1,20 g/L |
| carvalho (madeira) 0,60—0,90 g/cm 3 | etanol 0,79 g/cm 3 | oxigênio 1,31 g/L |
| ferro 7,9 g/cm 3 | acetona 0,79 g/cm 3 | nitrogênio 1,14 g/L |
| cobre 9,0 g/cm 3 | glicerina 1,26 g/cm 3 | dióxido de carbono 1,80 g/L |
| chumbo 11,3 g/cm 3 | azeite de oliva 0,92 g/cm 3 | hélio 0,16 g/L |
| prata 10,5 g/cm 3 | gasolina 0,70—0,77 g/cm 3 | néon 0,83 g/L |
| ouro 19,3 g/cm 3 | mercúrio 13,6 g/cm 3 | radônio 9,1 g/L |
Embora existam muitas maneiras de determinar a densidade de um objeto, talvez o método mais simples envolva encontrar separadamente a massa e o volume do objeto e, em seguida, dividir a massa da amostra pelo volume. No exemplo a seguir, a massa é encontrada diretamente pela pesagem, mas o volume é encontrado indiretamente por meio de medições de comprimento.
\[\mathrm{density=\dfrac{mass}{volume}} \nonumber \]
Cálculo da densidade O ouro — em tijolos, barras e moedas — tem sido uma forma de moeda por séculos. Para fazer com que as pessoas paguem por um tijolo de ouro sem realmente investir em um tijolo de ouro, as pessoas consideraram encher os centros dos tijolos de ouro ocos com chumbo para enganar os compradores fazendo-os pensar que o tijolo inteiro é ouro. Não funciona: o chumbo é uma substância densa, mas sua densidade não é tão grande quanto a do ouro, 19,3 g/cm 3. Qual é a densidade do chumbo se um cubo de chumbo tiver um comprimento de borda de 2,00 cm e uma massa de 90,7 g?
Solução
A densidade de uma substância pode ser calculada dividindo sua massa pelo volume. O volume de um cubo é calculado ao cubinar o comprimento da borda.
\[\mathrm{volume\: of\: lead\: cube=2.00\: cm\times2.00\: cm\times2.00\: cm=8.00\: cm^3} \nonumber \]
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{90.7\: g}{8.00\: cm^3}=\dfrac{11.3\: g}{1.00\: cm^3}=11.3\: g/cm^3} \nonumber \]
(Discutiremos o motivo do arredondamento para a primeira casa decimal na próxima seção.)
- Com três casas decimais, qual é o volume de um cubo (cm 3) com um comprimento de borda de 0,843 cm?
- Se o cubo na parte (a) for de cobre e tiver uma massa de 5,34 g, qual é a densidade do cobre com duas casas decimais?
- Responda a um
-
0,599 cm 3;
- Resposta b
-
8,91 g/cm 3
Essa simulação PhET ilustra outra maneira de determinar a densidade, usando o deslocamento da água. Determine a densidade dos blocos vermelho e amarelo.
Solução
Ao abrir a simulação de densidade e selecionar Mesma massa, você pode escolher entre vários blocos coloridos de 5,00 kg que podem ser jogados em um tanque contendo 100,00 L de água. O bloco amarelo flutua (é menos denso que a água) e o nível da água sobe para 105,00 L. Enquanto flutua, o bloco amarelo desloca 5,00 L de água, quantidade igual ao peso do bloco. O bloco vermelho afunda (é mais denso que a água, que tem densidade = 1,00 kg/L) e o nível da água sobe para 101,25 L.
O bloco vermelho, portanto, desloca 1,25 L de água, quantidade igual ao volume do bloco. A densidade do bloco vermelho é:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{1.25\: L}=4.00\: kg/L} \nonumber \]
Observe que, como o bloco amarelo não está completamente submerso, você não pode determinar sua densidade a partir dessas informações. Mas se você segurar o bloco amarelo no fundo do tanque, o nível da água sobe para 110,00 L, o que significa que agora ele desloca 10,00 L de água, e sua densidade pode ser encontrada:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{10.00\: L}=0.500\: kg/L} \nonumber \]
Remova todos os blocos da água e adicione o bloco verde ao tanque de água, colocando-o aproximadamente no meio do tanque. Determine a densidade do bloco verde.
- Resposta
-
2,00 kg/L
Resumo
As medições fornecem informações quantitativas que são essenciais para estudar e praticar química. Cada medição tem uma quantidade, uma unidade para comparação e uma incerteza. As medições podem ser representadas em notação decimal ou científica. Os cientistas usam principalmente o SI (Sistema Internacional) ou sistemas métricos. Usamos unidades básicas de SI, como metros, segundos e quilogramas, bem como unidades derivadas, como litros (para volume) e g/cm 3 (para densidade). Em muitos casos, achamos conveniente usar prefixos unitários que produzem unidades fracionárias e múltiplas, como microssegundos (10 −6 segundos) e megahertz (10 6 hertz), respectivamente.
Equações-chave
- \(\mathrm{density=\dfrac{mass}{volume}}\)
Glossário
- Celsius (°C)
- unidade de temperatura; a água congela a 0 °C e ferve a 100 °C nesta escala
- centímetro cúbico (cm 3 ou cc)
- volume de um cubo com um comprimento de borda de exatamente 1 cm
- metro cúbico (m 3)
- Unidade de volume SI
- densidade
- relação entre massa e volume de uma substância ou objeto
- Kelvin (K)
- Unidade SI de temperatura; 273,15 K = 0 ºC
- quilograma (kg)
- unidade de massa SI padrão; 1 kg = aproximadamente 2,2 libras
- comprimento
- medida de uma dimensão de um objeto
- litro (L)
- (também, decímetro cúbico) unidade de volume; 1 L = 1.000 cm 3
- metro (m)
- unidade métrica padrão e unidade SI de comprimento; 1 m = aproximadamente 1.094 jardas
- mililitro (mL)
- 1/1.000 de um litro; igual a 1 cm 3
- segundo (s)
- Unidade de tempo SI
- Unidades SI (Sistema Internacional de Unidades)
- padrões fixados por acordo internacional no Sistema Internacional de Unidades (Le Système International d'Unités)
- unidade
- padrão de comparação para medições
- volume
- quantidade de espaço ocupado por um objeto


