Matemática essencial
- Page ID
- 185078
Aritmética exponencial
A notação exponencial é usada para expressar números muito grandes e muito pequenos como um produto de dois números. O primeiro número do produto, o termo do dígito, geralmente é um número não inferior a 1 e não maior que 10. O segundo número do produto, o termo exponencial, é escrito como 10 com um expoente. Alguns exemplos de notação exponencial são:
\ [\ begin {align*}
1000&=1×10^3\\
100&=1×10^2\\
10&=1×10^1\\
1&=1×10^0\\
0,1&=1×10^ {−1}\\
0.001&=1×10^ {−3}\\
2386&=2,386×1000=2,386×10^3\\
0,123&=1,23 × 0,1 = 1,23 × 10^ { −1}
\ end {align*}\ nonumber\]
A potência (expoente) de 10 é igual ao número de casas em que o decimal é deslocado para dar o número do dígito. O método exponencial é uma notação particularmente útil para todos os números grandes e muito pequenos. Por exemplo, 1.230.000.000 = 1,23 × 10 9 e 0,0000000000036 = 3,6 × 10 −10.
Adição de exponenciais
Converta todos os números com a mesma potência de 10, adicione os termos dos dígitos e, se apropriado, converta o termo do dígito novamente em um número entre 1 e 10 ajustando o termo exponencial.
Adicione 5,00 × 10 −5 e 3,00 × 10 −3.
Solução em
\ [\ begin {align*}
3.00×10^ {−3} &=300×10^ {−5}\\
(5,00×10^ {−5}) + (300×10^ {−5}) &=305 × 10^ {−5} =3,05 × 10^ {−3}
\ end {align*}\ nonumber\]
Subtração de exponenciais
Converta todos os números na mesma potência de 10, calcule a diferença dos termos dos dígitos e, se apropriado, converta o termo do dígito novamente em um número entre 1 e 10 ajustando o termo exponencial.
Subtraia 4,0 × 10 −7 de 5,0 × 10 −6.
Solução em
\ [4,0×10^ {−7} =0,40×10^ {−6}\\
(5,0×10^ {−6}) − (0,40×10^ {−6}) =4,6×10^ {−6}\ nonumber\]
Multiplicação de exponenciais
Multiplique os termos dos dígitos da maneira usual e adicione os expoentes dos termos exponenciais.
Multiplique 4,2 × 10 −8 por 2,0 × 10 3.
Solução em
\[(4.2×10^{−8})×(2.0×10^3)=(4.2×2.0)×10^{(−8)+(+3)}=8.4×10^{−5} \nonumber \]
Divisão de exponenciais
Divida o termo do dígito do numerador pelo termo do dígito do denominador e subtraia os expoentes dos termos exponenciais.
Divida 3,6 × 10 5 por 6,0 × 10 −4.
Solução em
\[\dfrac{3.6×10^{−5}}{6.0×10^{−4}}=\left(\dfrac{3.6}{6.0}\right)×10^{(−5)−(−4)}=0.60×10^{−1}=6.0×10^{−2} \nonumber \]
Quadratura dos exponenciais
Faça o quadrado do termo do dígito da maneira usual e multiplique o expoente do termo exponencial por 2.
Elabore o número 4,0 × 10 −6.
Solução em
\[(4.0×10^{−6})^2=4×4×10^{2×(−6)}=16×10^{−12}=1.6×10^{−11} \nonumber \]
Cubagem de exponenciais
Cube o termo do dígito da maneira usual e multiplique o expoente do termo exponencial por 3.
Cube o número 2 × 10 4.
Solução em
\[(2×10^4)^3=2×2×2×10^{3×4}=8×10^{12} \nonumber \]
Obtendo raízes quadradas de exponenciais
Se necessário, diminua ou aumente o termo exponencial para que a potência de 10 seja uniformemente divisível por 2. Extraia a raiz quadrada do termo do dígito e divida o termo exponencial por 2.
Encontre a raiz quadrada de 1,6 × 10 −7.
Solução em
\ [\ begin {align*}
1,6 × 10^ {−7} &=16×10^ {−8}\\ sqrt {16×10^ {−8}} =
\ sqrt {16} ×\ sqrt {10^ {−8}} &=\ sqrt {16} ×10^ {−\ large {\ frac {8} {2}}} =4,0 × 10^ {−\ large {\ frac {8} {2}}} =4,0 × 10^ {−4}
\ end {align*}\ nonumber\]
Números significativos
Um apicultor relata que ele tem 525.341 abelhas. Os últimos três números do número são obviamente imprecisos, pois durante o tempo em que o guardião estava contando as abelhas, algumas delas morreram e outras eclodiram; isso torna muito difícil determinar o número exato de abelhas. Teria sido mais preciso se o apicultor tivesse relatado o número 525.000. Em outras palavras, os últimos três números não são significativos, exceto para definir a posição do ponto decimal. Seus valores exatos não têm significado útil nessa situação. Ao relatar qualquer informação como números, use apenas tantos números significativos quanto a precisão da medição garantir.
A importância de números significativos está em sua aplicação à computação fundamental. Além da adição e subtração, a soma ou diferença deve conter tantos dígitos à direita do decimal quanto os do menor número usado no cálculo (indicado por sublinhado no exemplo a seguir).
Adicione 4,383 g e 0,0023 g.
Solução em
\ [\ begin {align*}
&\ mathrm {4.38\ underline {3}\ :g}\\
&\ mathrm {\ underline {0.002\ underline {3}\ :g}\\
&\ mathrm {4.38\ underline {5}\ :g}
\ end {align*}\ nonumber\]
Na multiplicação e divisão, o produto ou quociente não deve conter mais dígitos do que o fator que contém o menor número de números significativos.
Multiplique 0,6238 por 6,6.
Solução em
\[0.623\underline{8}×6.\underline{6}=4.\underline{1} \nonumber \]
Ao arredondar números, aumente o dígito retido em 1 se ele for seguido por um número maior que 5 (“arredondar para cima”). Não altere o dígito retido se os dígitos seguintes forem menores que 5 (“arredondar para baixo”). Se o dígito retido for seguido por 5, arredonde para cima se o dígito retido for ímpar ou para baixo se for par (após o arredondamento, o dígito retido sempre será par).
O uso de logaritmos e números exponenciais
O logaritmo comum de um número (log) é a potência à qual 10 deve ser aumentado para igualar esse número. Por exemplo, o logaritmo comum de 100 é 2, porque 10 deve ser elevado à segunda potência para ser igual a 100. Veja a seguir exemplos adicionais.
| Número | Número expresso exponencialmente | Logaritmo comum |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Qual é o logaritmo comum de 60? Como 60 está entre 10 e 100, que têm logaritmos de 1 e 2, respectivamente, o logaritmo de 60 é 1,7782; ou seja,
\[60=10^{1.7782} \nonumber \]
O logaritmo comum de um número menor que 1 tem um valor negativo. O logaritmo de 0,03918 é −1,4069, ou
\[0.03918=10^{-1.4069}=\dfrac{1}{10^{1.4069}} \nonumber \]
Para obter o logaritmo comum de um número, use o botão de registro na sua calculadora. Para calcular um número a partir de seu logaritmo, pegue o log inverso do logaritmo ou calcule 10 x (onde x é o logaritmo do número).
O logaritmo natural de um número (ln) é a potência à qual e deve ser elevado para igualar o número; e é a constante 2,7182818. Por exemplo, o logaritmo natural de 10 é 2,303; ou seja,
\[10=e^{2.303}=2.7182818^{2.303} \nonumber \]
Para obter o logaritmo natural de um número, use o botão ln na sua calculadora. Para calcular um número a partir de seu logaritmo natural, insira o logaritmo natural e pegue o inverso ln do logaritmo natural ou calcule e x (onde x é o logaritmo natural do número).
Os logaritmos são expoentes; portanto, as operações que envolvem logaritmos seguem as mesmas regras das operações que envolvem expoentes.
- O logaritmo de um produto de dois números é a soma dos logaritmos dos dois números. \[\log xy= \log x + \log y, \textrm{ and }\ln xy=\ln x + \ln y \nonumber \]
- O logaritmo do número resultante da divisão de dois números é a diferença entre os logaritmos dos dois números. \[\log\dfrac{x}{y}=\log x-\log y,\textrm{ and } \ln\dfrac{x}{y}=\ln x-\ln y \nonumber \]
- O logaritmo de um número elevado a um expoente é o produto do expoente e o logaritmo do número. \[\log x^n=n\log x \textrm{ and }\ln x^n=n\ln x \nonumber \]
A solução de equações quadráticas
As funções matemáticas dessa forma são conhecidas como polinômios de segunda ordem ou, mais comumente, funções quadráticas.
\[ax^2+bx+c=0 \nonumber \]
A solução ou raízes de qualquer equação quadrática podem ser calculadas usando a seguinte fórmula:
\[x=\dfrac{-b±\sqrt{b^2−4ac}}{2a} \nonumber \]
Solução de equações quadráticas Resolva a equação quadrática 3 x 2 + 13 x − 10 = 0.
Solução Substituindo os valores a = 3, b = 13, c = −10 na fórmula, obtemos
\[x=\dfrac{−13±\sqrt{(13)^2−4×3×(−10)}}{2×3} \nonumber \]
\[x=\dfrac{−13±\sqrt{169+120}}{6}=\dfrac{−13±\sqrt{289}}{6}=\dfrac{−13±17}{6} \nonumber \]
As duas raízes são, portanto,
\[x=\dfrac{−13+17}{6}=\dfrac{2}{3}\textrm{ and }x=\dfrac{−13−17}{6}=−5 \nonumber \]
As equações quadráticas construídas em dados físicos sempre têm raízes reais e, dessas raízes reais, geralmente apenas aquelas com valores positivos têm alguma importância.
Gráficos bidimensionais (x - y)
A relação entre quaisquer duas propriedades de um sistema pode ser representada graficamente por um gráfico de dados bidimensional. Esse gráfico tem dois eixos: um horizontal correspondente à variável independente, ou a variável cujo valor está sendo controlado (x), e um eixo vertical correspondente à variável dependente, ou a variável cujo valor está sendo observado ou medido (y).
Quando o valor de y está mudando em função de x (ou seja, valores diferentes de x correspondem a diferentes valores de y), um gráfico dessa mudança pode ser plotado ou esboçado. O gráfico pode ser produzido usando valores específicos para pares de dados (x, y).
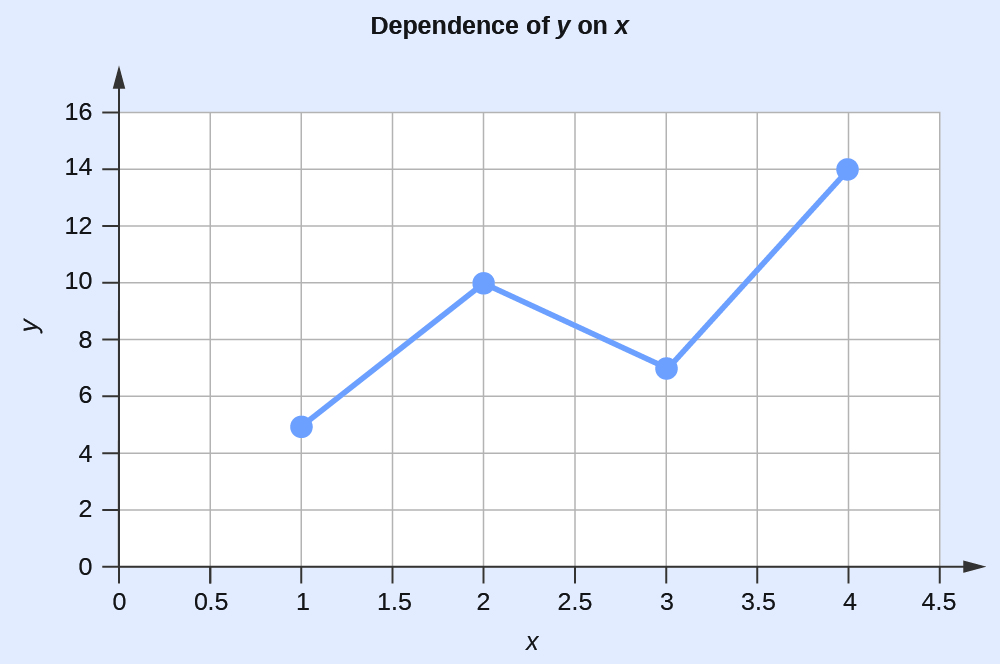
Representando graficamente a dependência de y em x
| x | y |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 7 |
| 4 | 14 |
Esta tabela contém os seguintes pontos: (1,5), (2,10), (3,7) e (4,14). Cada um desses pontos pode ser plotado em um gráfico e conectado para produzir uma representação gráfica da dependência de y em x.
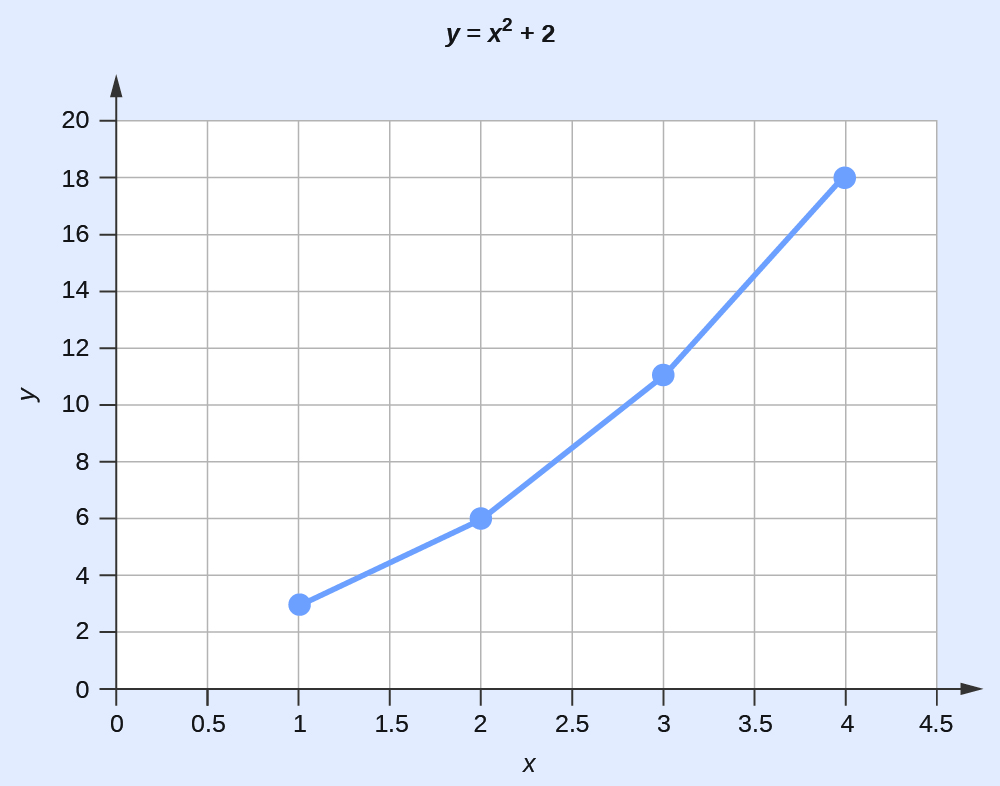
Se a função que descreve a dependência de y em x for conhecida, ela poderá ser usada para calcular pares de dados x, y que podem ser plotados posteriormente.
Plotting Data Pairs If we know that y = x2 + 2, we can produce a table of a few (x,y) values and then plot the line based on the data shown here.
| x | y = x2 + 2 |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 11 |
| 4 | 18 |