21.3: Decaimento radioativo

objetivos de aprendizagem

• Reconheça os modos comuns de decaimento radioativo
• Identifique partículas e energias comuns envolvidas nas reações de decaimento nuclear
• Escreva e equilibre equações de decaimento nuclear
• Calcule parâmetros cinéticos para processos de decaimento, incluindo meia-vida
• Descreva técnicas comuns de datação radiométrica

Após a descoberta um tanto fortuita da radioatividade por Becquerel, muitos cientistas proeminentes começaram a investigar esse fenômeno novo e intrigante. Entre eles estavam Marie Curie (a primeira mulher a ganhar um Prêmio Nobel e a única pessoa a ganhar dois prêmios Nobel em ciências diferentes - química e física), que foi a primeira a cunhar o termo “radioatividade”, e Ernest Rutherford (famoso por experimentos de folha de ouro), que investigou e nomeou três dos mais comuns tipos de radiação. Durante o início do século XX, muitas substâncias radioativas foram descobertas, as propriedades da radiação foram investigadas e quantificadas e uma sólida compreensão da radiação e do decaimento nuclear foi desenvolvida.

A mudança espontânea de um nuclídeo instável em outro é o decaimento radioativo. O nuclídeo instável é chamado de nuclídeo pai; o nuclídeo que resulta da decomposição é conhecido como nuclídeo filho. O nuclídeo filho pode ser estável ou pode se decompor sozinho. A radiação produzida durante o decaimento radioativo é tal que o nuclídeo filho fica mais próximo da faixa de estabilidade do que o nuclídeo original, portanto, a localização de um nuclídeo em relação à faixa de estabilidade pode servir como um guia para o tipo de decaimento que ele sofrerá (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Um núcleo de urânio-238 (o nuclídeo parental) sofre decaimento α para formar tório-234 (o nuclídeo filho). A partícula alfa remove dois prótons (verdes) e dois nêutrons (cinza) do núcleo urânio-238.

Um diagrama mostra duas esferas compostas por muitas esferas brancas e verdes menores conectadas por uma seta voltada para a direita com outra flecha voltada para baixo saindo dela. A esfera esquerda, chamada “núcleo principal de urânio traço 238”, tem duas esferas brancas e duas verdes que estão próximas uma da outra e são delineadas em vermelho. Essas duas esferas verdes e duas brancas são mostradas perto da ponta da seta voltada para baixo e rotuladas como “partícula alfa”. A esfera direita, chamada “Daughter nucleus radon dash 234”, tem a mesma aparência da esquerda, mas tem um espaço para quatro esferas menores delineadas com uma linha pontilhada vermelha.

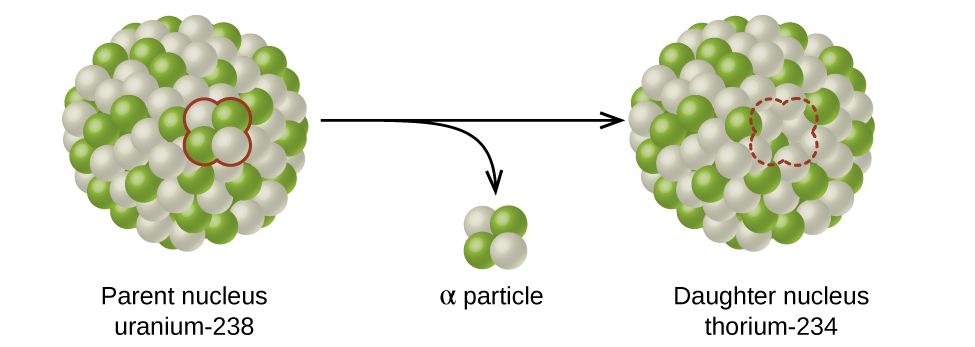
Embora o decaimento radioativo de um núcleo seja muito pequeno para ser visto a olho nu, podemos ver indiretamente o decaimento radioativo em um ambiente chamado câmara de nuvem. Clique aqui para saber mais sobre câmaras de nuvem e ver uma interessante demonstração da câmara de nuvem do Jefferson Lab.

Vídeo\(\PageIndex{1}\): Como construir uma câmara de nuvem!

Tipos de decaimento radioativo

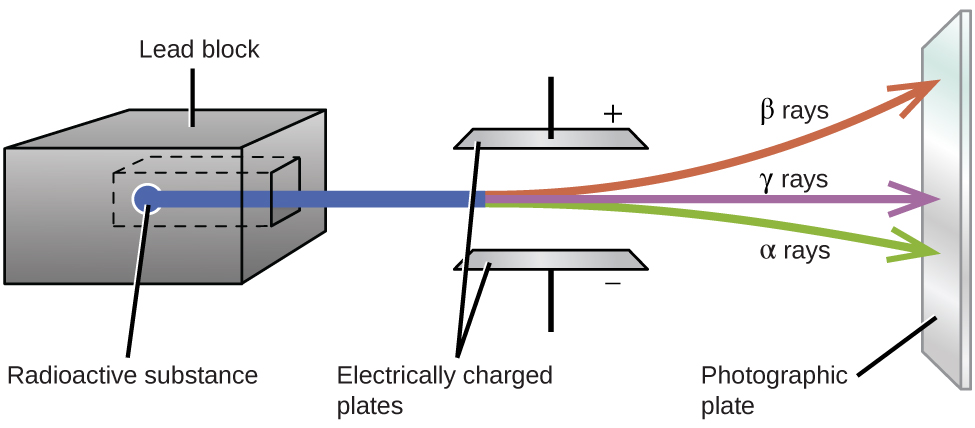
Os experimentos de Ernest Rutherford envolvendo a interação da radiação com um campo magnético ou elétrico (Figura\(\PageIndex{2}\)) o ajudaram a determinar que um tipo de radiação consistia em\(α\) partículas carregadas positivamente e relativamente massivas; um segundo tipo era composto de carga negativa e muito menos \(β\)partículas massivas; e uma terceira eram ondas eletromagnéticas não carregadas,\(γ\) raios. Agora sabemos que\(α\) as partículas são núcleos de hélio de alta energia,\(β\) as partículas são elétrons de alta energia e a\(γ\) radiação compõe radiação eletromagnética de alta energia. Classificamos diferentes tipos de decaimento radioativo pela radiação produzida.

Figura\(\PageIndex{2}\): As partículas alfa, que são atraídas para a placa negativa e desviadas em uma quantidade relativamente pequena, devem ser carregadas positivamente e relativamente massivas. As partículas beta, que são atraídas para a placa positiva e desviadas em uma quantidade relativamente grande, devem ser carregadas negativamente e relativamente leves. Os raios gama, que não são afetados pelo campo elétrico, devem estar descarregados.

Um diagrama é mostrado. Uma caixa cinza no lado esquerdo do diagrama chamada “Bloco de chumbo” tem uma câmara escavada no centro na qual uma amostra rotulada como “Substância radioativa” é colocada. Um feixe azul está saindo da amostra, saindo do bloco e passando por duas placas colocadas horizontalmente que são rotuladas como “Placas carregadas eletricamente”. A placa superior é rotulada com um sinal positivo, enquanto a placa inferior é rotulada com um sinal negativo. É mostrado que o feixe se divide em três feixes à medida que passa entre as placas; em ordem, de cima para baixo, eles são vermelhos, rotulados como “raios beta”, roxos rotulados como “raios gama” e verdes rotulados como “raios alfa”. É mostrado que as vigas atingem uma placa vertical chamada “Placa fotográfica” no lado direito do diagrama.

Alfa (\(α\)) decayé a emissão de uma partícula α do núcleo. Por exemplo, o polônio-210 sofre decaimento α:

\[\ce{^{210}_{84}Po⟶ ^4_2He + ^{206}_{82}Pb} \hspace{40px}\ce{or}\hspace{40px} \ce{^{210}_{84}Po ⟶ ^4_2α + ^{206}_{82}Pb}\nonumber \]

O decaimento alfa ocorre principalmente em núcleos pesados (A > 200, Z > 83). Como a perda de uma partícula α dá a um nuclídeo filho com um número de massa quatro unidades menor e um número atômico duas unidades menor que o do nuclídeo pai, o nuclídeo filho tem uma razão n:p maior do que o nuclídeo pai. Se o nuclídeo pai que sofre decaimento α estiver abaixo da faixa de estabilidade, o nuclídeo filho ficará mais próximo da banda.

O decaimento beta (β) é a emissão de um elétron de um núcleo. O iodo-131 é um exemplo de um nuclídeo que sofre decaimento β:

\[\ce{^{131}_{53}I ⟶ ^0_{-1}e + ^{131}_{54}X} \hspace{40px}\ce{or}\hspace{40px} \ce{^{131}_{53}I ⟶ ^0_{-1}β + ^{131}_{54}Xe}\nonumber \]

O decaimento beta, que pode ser considerado como a conversão de um nêutron em um próton e uma partícula β, é observado em nuclídeos com uma grande proporção n:p. A partícula beta (elétron) emitida é do núcleo atômico e não é um dos elétrons ao redor do núcleo. Esses núcleos estão acima da faixa de estabilidade. A emissão de um elétron não altera o número de massa do nuclídeo, mas aumenta o número de seus prótons e diminui o número de seus nêutrons. Consequentemente, a relação n:p é reduzida e o nuclídeo filho fica mais próximo da faixa de estabilidade do que o nuclídeo original.

A emissão gama (emissão γ) é observada quando um nuclídeo é formado em um estado excitado e depois decai para seu estado fundamental com a emissão de um raio γ, um quantum de radiação eletromagnética de alta energia. A presença de um núcleo em estado excitado geralmente é indicada por um asterisco (*). O cobalto-60 emite radiação γ e é usado em muitas aplicações, incluindo tratamento de câncer:

\[\mathrm{^{60}_{27}Co^* ⟶\, ^0_0γ +\, ^{60}_{27}Co}\nonumber \]

Não há mudança no número de massa ou no número atômico durante a emissão de um raio γ, a menos que a emissão γ acompanhe um dos outros modos de decaimento.

O íon emissor de pósitrons (\(β^+\)decaimento) é a emissão de um pósitron do núcleo. O oxigênio-15 é um exemplo de nuclídeo que sofre emissão de pósitrons:

\[\ce{^{15}_8O ⟶ ^0_{+1}e + ^{15}_7N} \hspace{40px}\ce{or}\hspace{40px} \ce{^{15}_8O ⟶ ^0_{+1}β + ^{15}_7N}\nonumber \]

A emissão de pósitrons é observada para nuclídeos nos quais a relação n:p é baixa. Esses nuclídeos estão abaixo da faixa de estabilidade. O decaimento do pósitron é a conversão de um próton em nêutron com a emissão de um pósitron. A relação n:p aumenta e o nuclídeo filho fica mais próximo da faixa de estabilidade do que o nuclídeo original.

A captura de elétrons ocorre quando um dos elétrons internos de um átomo é capturado pelo núcleo do átomo. Por exemplo, o potássio-40 sofre captura de elétrons:

\[\ce{^{40}_{19}K + ^0_{-1}e ⟶ ^{40}_{18}Ar}\nonumber \]

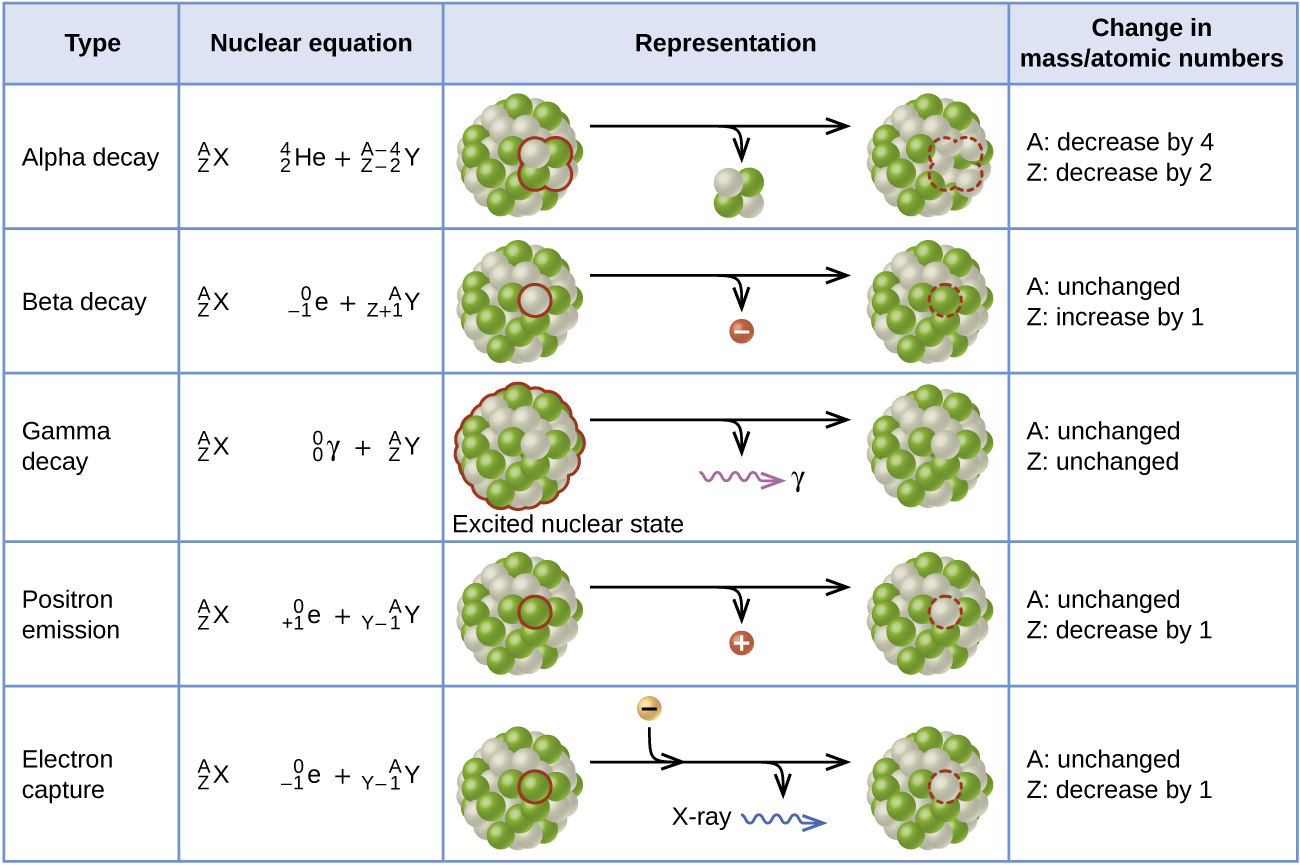
A captura de elétrons ocorre quando um elétron da camada interna se combina com um próton e é convertido em um nêutron. A perda de um elétron da camada interna deixa uma vaga que será preenchida por um dos elétrons externos. Quando o elétron externo cair na vaga, ele emitirá energia. Na maioria dos casos, a energia emitida será na forma de um raio-X. Assim como a emissão de pósitrons, a captura de elétrons ocorre para núcleos “ricos em prótons” que estão abaixo da faixa de estabilidade. A captura de elétrons tem o mesmo efeito no núcleo que a emissão de pósitrons: o número atômico é reduzido em um e o número de massa não muda. Isso aumenta a relação n:p, e o nuclídeo filho fica mais próximo da faixa de estabilidade do que o nuclídeo original. É difícil prever se a captura de elétrons ou a emissão de pósitrons ocorrem. A escolha se deve principalmente a fatores cinéticos, com aquele que requer menor energia de ativação sendo o mais provável de ocorrer. A figura\(\PageIndex{3}\) resume esses tipos de decaimento, junto com suas equações e mudanças nos números atômicos e de massa.

Figura\(\PageIndex{3}\): Esta tabela resume o tipo, a equação nuclear, a representação e quaisquer alterações na massa ou nos números atômicos para vários tipos de decaimento.

Essa tabela tem quatro colunas e seis linhas. A primeira linha é uma linha de cabeçalho e ela rotula cada coluna: “Tipo”, “Equação nuclear”, “Representação” e “Mudança na massa/números atômicos”. Sob a coluna “Tipo” estão os seguintes: “Decaimento alfa”, “Decaimento beta”, “Decaimento gama”, “Emissão de pósitrons” e “Captura de elétrons”. Sob a coluna “Equação nuclear” existem várias equações. Cada um começa com o sobrescrito A empilhado sobre o subscrito Z X. Há uma grande lacuna de espaço e, em seguida, as seguintes equações: “sobrescrito 4 empilhado sobre o subscrito 2 Ele mais sobrescrito A menos 4 empilhado sobre o subscrito Z menos 2 Y”, “sobrescrito 0 empilhado sobre o subscrito negativo 1 e mais o sobrescrito A empilhado subscrito Z mais 1 Y”, “sobrescrito 0 empilhado sobre subscrito 0 gama minúscula mais sobrescrito A empilhado sobre o subscrito Z Y”, “sobrescrito 0 empilhado sobre subscrito positivo 1 e mais sobrescrito A empilhado sobre o subscrito Y menos 1 Y” e “sobrescrito 0 empilhado sobre o subscrito negativo 1 e mais sobrescrito A empilhados sobre o subscrito Y menos 1 Y.” Sob a coluna “Representação” estão os cinco diagramas. O primeiro mostra um conjunto de esferas verdes e brancas. Uma seção do cluster contendo duas esferas brancas e duas verdes é delineada. Há uma seta voltada para a direita apontando para um agrupamento semelhante ao descrito anteriormente, mas a seção delineada está ausente. Da flecha, outra flecha se ramifica e aponta para baixo. O pequeno aglomerado de duas esferas brancas e duas esferas verdes aparece no final da seta. O diagrama a seguir mostra o mesmo conjunto de esferas brancas e verdes. Uma esfera branca é delineada. Há uma seta voltada para a direita em um cluster similar, mas a esfera branca está ausente. Outra flecha se ramifica da seta principal e uma esfera vermelha com um sinal negativo aparece no final. O diagrama a seguir mostra o mesmo conjunto de esferas brancas e verdes. Toda a esfera é delineada e rotulada como “estado nuclear excitado”. Há uma seta voltada para a direita que aponta para o mesmo agrupamento. Não faltam esferas. Fora da seta principal está outra seta que aponta para uma flecha rabiscada roxa que, por sua vez, aponta para uma gama minúscula. O diagrama a seguir mostra o mesmo conjunto de esferas brancas e verdes. Uma esfera verde é delineada. Há uma seta voltada para a direita em um cluster similar, mas a esfera verde está ausente. Outra flecha se ramifica da seta principal e uma esfera vermelha com um sinal positivo aparece no final. O diagrama a seguir mostra o mesmo conjunto de esferas brancas e verdes. Uma esfera verde é delineada. Há uma seta voltada para a direita em um cluster similar, mas a esfera verde está ausente. Duas outras flechas se ramificam da seta principal. A primeira mostra uma esfera dourada com um sinal negativo se unindo à seta voltada para a direita. O segundo aponta para uma seta rabiscada azul chamada “Raio-X”. Na coluna “Mudança na massa/números atômicos” estão os seguintes: “A: diminuição em 4, Z: diminuição em 2”, “A: inalterado, Z: aumentado em 1”, “A: inalterado, Z: inalterado”, “A: inalterado, Z: inalterado”, “A: inalterado, Z: diminuição em 1” e “A: inalterado, Z: diminuição em 1” e “A: inalterado, Z: diminuição em 1” e “A: inalterado, Z: diminuição em 1”.

PET Scan

Os exames de tomografia por emissão de pósitrons (PET) usam radiação para diagnosticar e rastrear condições de saúde e monitorar tratamentos médicos, revelando como partes do corpo de um paciente funcionam (Figura\(\PageIndex{4}\)). Para realizar uma tomografia computadorizada, um radioisótopo emissor de pósitrons é produzido em um ciclotron e, em seguida, ligado a uma substância usada pela parte do corpo que está sendo investigada. Esse composto “marcado”, ou radiotraçador, é então colocado no paciente (injetado via intravenosa ou respirado como um gás) e, como é usado pelo tecido, revela como esse órgão ou outra área do corpo funciona.

Figura\(\PageIndex{4}\): Um scanner PET (a) usa radiação para fornecer uma imagem de como parte do corpo de um paciente funciona. Os exames que ele produz podem ser usados para obter imagens de um cérebro saudável (b) ou para diagnosticar condições médicas, como a doença de Alzheimer (c). (crédito a: modificação da obra de Jens Maus)

Três figuras são mostradas e rotuladas como “a”, “b” e “c”. A figura a mostra uma máquina com uma abertura redonda conectada a uma mesa de exame. A figura b é um exame médico da parte superior da cabeça de uma pessoa e mostra grandes manchas amarelas e vermelhas e manchas menores de azul, verde e roxo. A figura c também mostra um exame médico do topo da cabeça de uma pessoa, mas essa imagem é principalmente colorida em azul e roxo com manchas muito pequenas de vermelho e amarelo.

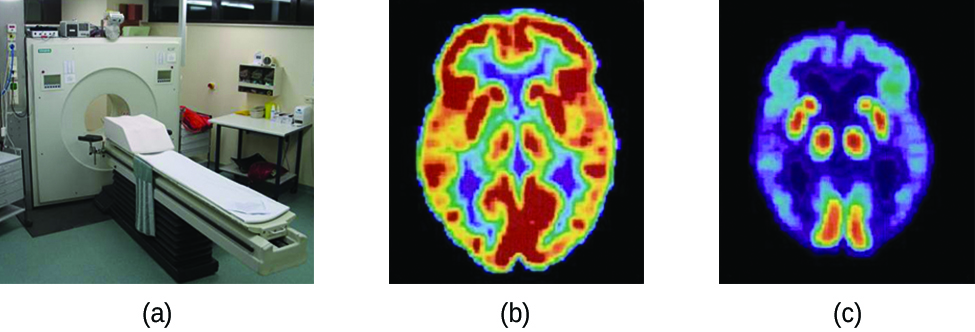
Por exemplo, o F-18 é produzido por bombardeio de prótons de ¹⁸ O\( (\ce{^{18}_8O + ^1_1p⟶ ^{18}_9F + ^1_0n})\) e incorporado a um análogo da glicose chamado fludeoxiglicose (FDG). A forma como o FDG é usado pelo corpo fornece informações diagnósticas críticas; por exemplo, como os cânceres usam glicose de forma diferente dos tecidos normais, o FDG pode revelar cânceres. O ¹⁸ F emite pósitrons que interagem com elétrons próximos, produzindo uma explosão de radiação gama. Essa energia é detectada pelo scanner e convertida em uma imagem colorida tridimensional detalhada que mostra como essa parte do corpo do paciente funciona. Níveis diferentes de radiação gama produzem diferentes quantidades de brilho e cores na imagem, que podem então ser interpretadas por um radiologista para revelar o que está acontecendo. Os exames PET podem detectar danos cardíacos e doenças cardíacas, ajudar a diagnosticar a doença de Alzheimer, indicar a parte do cérebro que é afetada pela epilepsia, revelar o câncer, mostrar em que estágio ele está e o quanto ele se espalhou e se os tratamentos são eficazes. Ao contrário da ressonância magnética e dos raios-X, que mostram apenas a aparência de algo, a grande vantagem dos exames de PET é que eles mostram como algo funciona. Agora, os exames de PET geralmente são realizados em conjunto com uma tomografia computadorizada.

Série Radioactive Decay

Os isótopos radioativos que ocorrem naturalmente dos elementos mais pesados se enquadram em cadeias de sucessivas desintegrações, ou decaimentos, e todas as espécies em uma cadeia constituem uma família radioativa, ou série de decaimento radioativo. Três dessas séries incluem a maioria dos elementos naturalmente radioativos da tabela periódica. Eles são a série do urânio, a série dos actinídeos e a série do tório. A série neptúnio é uma quarta série, que não é mais significativa na Terra devido à curta meia-vida das espécies envolvidas. Cada série é caracterizada por um pai (primeiro membro) que tem uma meia-vida longa e uma série de nuclídeos filhos que, em última análise, levam a um produto final estável - ou seja, um nuclídeo na faixa de estabilidade (Figura\(\PageIndex{5}\)). Em todas as três séries, o produto final é um isótopo estável de chumbo. A série neptúnio, anteriormente pensada para terminar com bismuto-209, termina com tálio-205.

Figura\(\PageIndex{5}\): O urânio-238 sofre uma série de decaimento radioativo que consiste em 14 etapas separadas antes de produzir chumbo-206 estável. Esta série consiste em oito\(α\) decaimentos e seis\(β\) decaimentos.

É mostrado um gráfico onde o eixo x é rotulado como “Número de nêutrons, parênteses abertos, n, parênteses próximos” e tem valores de 122 a 148 em incrementos de 2. O eixo y é rotulado como “Número atômico” e tem valores de 80 a 92 em incrementos de 1. Dois tipos de setas são usados neste gráfico para conectar os pontos. As setas verdes são rotuladas como “decaimento alfa”, enquanto as setas vermelhas são rotuladas como “decaimento beta”. Começando no ponto “92, 146” que é rotulado como “sobrescrito 238, U”, uma seta verde conecta esse ponto ao segundo ponto “90, 144”, que é rotulado como “sobrescrito 234, T h”. Uma seta vermelha conecta isso ao terceiro ponto “91, 143”, que é rotulado como “sobrescrito 234, P a”, que é conectado ao quarto ponto “92, 142” por uma seta vermelha e é rotulado como “sobrescrito 234, U.” Uma seta verde leva ao próximo ponto, “90, 140”, que é rotulado como “sobrescrito 230, T h” e é conectado por uma seta verde ao sexto ponto, “88, 138” que é rotulado como “sobrescrito 226, R a” que, por sua vez, é conectado por uma seta verde ao sétimo ponto “86, 136”, que é rotulado como “sobrescrito 222, Ra”. O oitavo ponto, em “84, 134”, é rotulado como “sobrescrito 218, P o” e tem setas verdes que levam a ele e se afastam dele até o nono ponto “82, 132”, que é rotulado como “sobrescrito 214, Pb”, que é conectado por uma seta vermelha ao décimo ponto, “83, 131”, que é rotulado como “sobrescrito 214, B i”. Uma seta vermelha leva ao décimo primeiro ponto “84, 130”, que é rotulado como “sobrescrito 214, P o” e uma seta verde leva ao décimo segundo ponto “82, 128”, que é rotulado como “sobrescrito 210, P b”. Uma seta vermelha leva ao décimo terceiro ponto “83, 127”, que é rotulado como “sobrescrito 210, B i” e uma seta vermelha leva ao décimo quarto ponto “84, 126”, que é rotulado como “sobrescrito 210, P o.” O ponto final é rotulado como “82, 124” e “sobrescrito 206, P b.”.

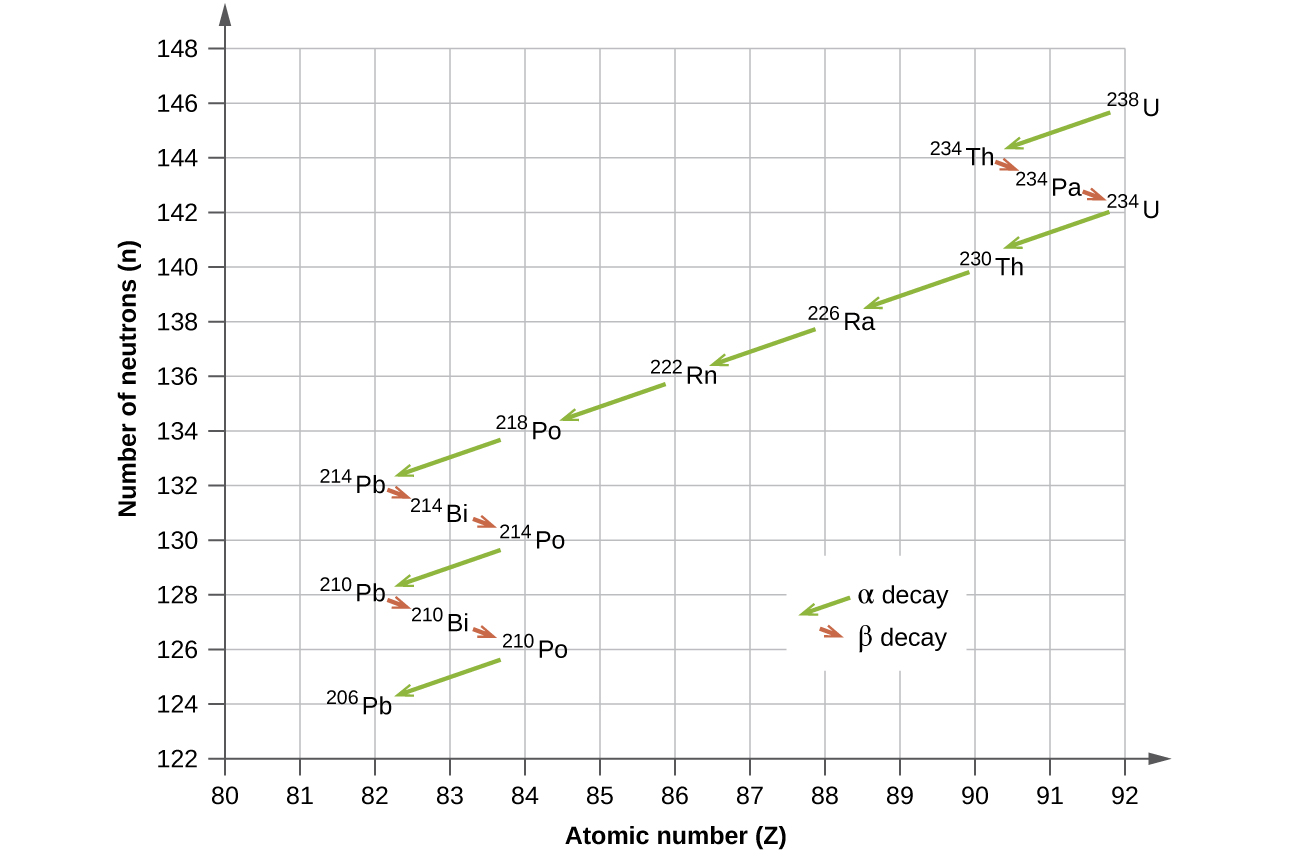
Meias-vidas radioativas

O decaimento radioativo segue a cinética de primeira ordem. Como as reações de primeira ordem já foram abordadas em detalhes no capítulo de cinética, agora aplicaremos esses conceitos às reações de decaimento nuclear. Cada nuclídeo radioativo tem uma meia-vida característica e constante (t _1/2), o tempo necessário para que metade dos átomos em uma amostra se decomponha. A meia-vida de um isótopo nos permite determinar por quanto tempo uma amostra de um isótopo útil estará disponível, e por quanto tempo uma amostra de um isótopo indesejável ou perigoso deve ser armazenada antes de decair para um nível de radiação baixo o suficiente que não seja mais um problema.

Por exemplo, o cobalto-60, um isótopo que emite raios gama usados para tratar o câncer, tem meia-vida de 5,27 anos (Figura\(\PageIndex{6}\)). Em uma determinada fonte de cobalto-60, como metade dos\(\ce{^{60}_{27}Co}\) núcleos se decompõe a cada 5,27 anos, tanto a quantidade de material quanto a intensidade da radiação emitida são reduzidas pela metade a cada 5,27 anos. (Observe que, para uma determinada substância, a intensidade da radiação que ela produz é diretamente proporcional à taxa de decaimento da substância e à quantidade da substância.) Isso é o esperado para um processo que segue uma cinética de primeira ordem. Portanto, uma fonte de cobalto-60 usada no tratamento do câncer deve ser substituída regularmente para continuar sendo eficaz.

Figura\(\PageIndex{6}\): Para o cobalto-60, que tem meia-vida de 5,27 anos, 50% permanecem após 5,27 anos (uma meia-vida), 25% permanecem após 10,54 anos (duas meias-vidas), 12,5% permanecem após 15,81 anos (três meias-vidas) e assim por diante.

Um gráfico, intitulado “C o traço 60 Decay”, é mostrado onde o eixo x é rotulado como “C o traço 60 restante, parêntese aberto, sinal de porcentagem, parêntese de fechamento” e tem valores de 0 a 100 em incrementos de 25. O eixo y é rotulado como “Número de vidas de meio traço” e tem valores de 0 a 5 em incrementos de 1. O primeiro ponto, em “0, 100”, tem um círculo cheio de pequenos pontos desenhados perto dele, rotulado como “10 g”. O segundo ponto, em “1,50”, tem um círculo menor preenchido com pequenos pontos desenhados perto dele, rotulado como “5 g”. O terceiro ponto, em “2, 25”, tem um pequeno círculo cheio de pequenos pontos desenhados perto dele, rotulado como “2,5 g”. O quarto ponto, em “3.12,5”, tem um círculo muito pequeno cheio de pequenos pontos desenhados perto dele, rotulado como “1,25 g”. O último ponto, em “4, 6,35”, tem um pequeno círculo cheio de pequenos pontos desenhados perto dele rotulados.” 625 g.”

Como o decaimento nuclear segue a cinética de primeira ordem, podemos adaptar as relações matemáticas usadas para reações químicas de primeira ordem. Geralmente substituímos o número de núcleos, N, pela concentração. Se a taxa for declarada em decaimentos nucleares por segundo, nos referimos a ela como a atividade da amostra radioativa. A taxa de decaimento radioativo é:

\[\text{decay rate} = \lambda N\nonumber \]

com\(\lambda\) é a constante de decaimento do radioisótopo específico.

A constante de decaimento,\(\lambda\), que é o mesmo que uma constante de taxa discutida no capítulo de cinética. É possível expressar a constante de decaimento em termos de meia-vida, t _1/2:

\[λ=\dfrac{\ln 2}{t_{1/2}}=\dfrac{0.693}{t_{1/2}} \hspace{40px}\ce{or}\hspace{40px} t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\nonumber \]

As equações de primeira ordem que relacionam quantidade, N e tempo são:

\[N_t=N_0e^{−kt} \hspace{40px}\ce{or}\hspace{40px} t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]

onde N ₀ é o número inicial de núcleos ou moles do isótopo, e N _t é o número de núcleos/moles restantes no tempo t. \(\PageIndex{1}\)O exemplo aplica esses cálculos para encontrar as taxas de decaimento radioativo para nuclídeos específicos.

Exemplo\(\PageIndex{1}\): Rates of Radioactive Decay

\(\ce{^{60}_{27}Co}\)decai com meia-vida de 5,27 anos para produzir\(\ce{^{60}_{28}Ni}\).

1. Qual é a constante de decaimento da desintegração radioativa do cobalto-60?
2. Calcule a fração de uma amostra do\(\ce{^{60}_{27}Co}\) isótopo que permanecerá após 15 anos.
3. Quanto tempo leva para uma amostra de\(\ce{^{60}_{27}Co}\) se desintegrar na medida em que restam apenas 2,0% da quantidade original?

Solução

(a) O valor da constante de taxa é dado por:

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5.27\:y}=0.132\:y^{−1}} \nonumber \]

(b) A fração\(\ce{^{60}_{27}Co}\) disso é deixada após o tempo t ser dado por\(\dfrac{N_t}{N_0}\). Reorganizar a relação de primeira ordem N _t = N ₀ e ^{— λt} para resolver essa razão produz:

\[\dfrac{N_t}{N_0}=e^{-λt}=e^\mathrm{-(0.132/y)(15.0/y)}=0.138 \nonumber \]

A fração\(\ce{^{60}_{27}Co}\) disso permanecerá após 15,0 anos é 0,138. Ou dito de outra forma, 13,8% do presente\(\ce{^{60}_{27}Co}\) originalmente permanecerá após 15 anos.

(c) 2,00% da quantidade original de\(\ce{^{60}_{27}Co}\) é igual a 0,0200 × N ₀. Substituindo isso na equação do tempo pela cinética de primeira ordem, temos:

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)=−\dfrac{1}{0.132\:\ce y^{−1}}\ln\left(\dfrac{0.0200×N_0}{N_0}\right)=29.6\:\ce y \nonumber \]

Exercício\(\PageIndex{1}\)

Radon-222,\(\ce{^{222}_{86}Rn}\), tem meia-vida de 3.823 dias. Quanto tempo uma amostra de radônio-222 com uma massa de 0,750 g levará para se decompor em outros elementos, restando apenas 0,100 g de radônio-222?

Resposta

11,1 dias

Como cada nuclídeo tem um número específico de nucleons, um equilíbrio particular de repulsão e atração e seu próprio grau de estabilidade, as meias-vidas dos nuclídeos radioativos variam amplamente. Por exemplo: a meia-vida de\(\ce{^{209}_{83}Bi}\) é 1,9 × 10 ¹⁹ anos;\(\ce{^{239}_{94}Ra}\) é 24.000 anos;\(\ce{^{222}_{86}Rn}\) é 3,82 dias; e o elemento-111 (Rg para roentgenium) é 1,5 × 10 ^—3 segundos. As meias-vidas de vários isótopos radioativos importantes para a medicina são mostradas na Tabela\(\PageIndex{1}\), e outros estão listados no Apêndice N1.

Tabela\(\PageIndex{1}\): Meias-vidas de isótopos radioativos importantes para a medicina

Tipo	Modo de decaimento	Meia-vida	Usos
F-18	decaimento β ^+	110. minutos	Exames PET
Co-60	decaimento β, decaimento γ	5,27 anos	tratamento do câncer
TC-99 m ^1	decaimento γ	8,01 horas	exames de cérebro, pulmão, coração, osso
I-131	decaimento β	8,02 dias	exames e tratamento da tireoide
Tl-201	captura de elétrons	73 horas	exames de coração e artérias; testes de estresse cardíaco
O “m” em TC-99m significa “metaestável”, indicando que esse é um estado instável e de alta energia do Tc-99. Isótopos metaestáveis emitem\(γ\) radiação para se livrar do excesso de energia e se tornarem (mais) estáveis.

Datação radiométrica

Vários radioisótopos têm meia-vida e outras propriedades que os tornam úteis para fins de “datação” da origem de objetos, como artefatos arqueológicos, organismos anteriormente vivos, ou formações geológicas. Esse processo é de datação radiométrica e tem sido responsável por muitas descobertas científicas inovadoras sobre a história geológica da Terra, a evolução da vida, e a história da civilização humana. Vamos explorar alguns dos tipos mais comuns de datação radioativa e como os isótopos específicos funcionam para cada tipo.

Datação radioativa usando carbono-14

A radioatividade do carbono-14 fornece um método para datar objetos que faziam parte de um organismo vivo. Esse método de datação radiométrica, também chamado de datação por radiocarbono ou datação por carbono-14, é preciso para datar substâncias que contêm carbono com até cerca de 30.000 anos e pode fornecer datas razoavelmente precisas até um máximo de cerca de 50.000 anos.

O carbono que ocorre naturalmente consiste em três isótopos:\(\ce{^{12}_6C}\), que constitui cerca de 99% do carbono na Terra;\(\ce{^{13}_6C}\), cerca de 1% do total; e vestígios de\(\ce{^{14}_6C}\). O carbono-14 se forma na alta atmosfera pela reação de átomos de nitrogênio com nêutrons dos raios cósmicos no espaço:

\[\ce{^{14}_7N + ^1_0n⟶ ^{14}_6C + ^1_1H}\nonumber \]

Todos os isótopos de carbono reagem com o oxigênio para produzir moléculas de CO ₂. A proporção de\(\ce{^{14}_6CO2}\) para\(\ce{^{12}_6CO2}\) depende da proporção de\(\ce{^{14}_6CO}\) para\(\ce{^{12}_6CO}\) na atmosfera. A abundância natural de\(\ce{^{14}_6CO}\) na atmosfera é de aproximadamente 1 parte por trilhão; até recentemente, isso geralmente era constante ao longo do tempo, como visto em amostras de gás encontradas presas no gelo. A incorporação de\(\ce{^{14}_6C ^{14}_6CO2}\) e\(\ce{^{12}_6CO2}\) nas plantas é uma parte regular do processo de fotossíntese, o que significa que a\(\ce{^{14}_6C: ^{12}_6C}\) proporção encontrada em uma planta viva é a\(\ce{^{14}_6C: ^{12}_6C}\) mesma da atmosfera. Mas quando a planta morre, ela não retém mais carbono por meio da fotossíntese. \(\ce{^{12}_6C}\)Por ser um isótopo estável e não sofrer decaimento radioativo, sua concentração na planta não muda. No entanto, o carbono-14 decai por emissão β com meia-vida de 5730 anos:

\[\ce{^{14}_6C⟶ ^{14}_7N + ^0_{-1}e}\nonumber \]

Assim, a\(\ce{^{14}_6C: ^{12}_6C}\) proporção diminui gradualmente após a morte da planta. A diminuição da proporção com o tempo fornece uma medida do tempo decorrido desde a morte da planta (ou outro organismo que a comeu). A figura retrata\(\PageIndex{7}\) visualmente esse processo.

Figura\(\PageIndex{7}\): Junto com o carbono-12 estável, o carbono radioativo 14 é absorvido por plantas e animais e permanece em um nível constante dentro deles enquanto estão vivos. Após a morte, o C-14 decai e a relação C-14:C-12 nos restos mortais diminui. Comparar essa proporção com a proporção C-14:C-12 em organismos vivos nos permite determinar há quanto tempo o organismo viveu (e morreu).

Um diagrama mostra uma vaca parada no chão ao lado de uma árvore. No canto superior esquerdo do diagrama, onde o céu está representado, uma única esfera branca é mostrada e é conectada por uma seta voltada para baixo a uma esfera maior composta por esferas verdes e brancas que é rotulada como “sobrescrito 14, subscrito 7, N.” Essa estrutura é conectada a outras três estruturas por uma seta voltada para a direita. Cada uma das três que aponta é composta por esferas verdes e brancas e todas têm setas apontando delas para o chão. O primeiro deles é rotulado como “Rastreamento, sobrescrito 14, subscrito 6, C”, o segundo é rotulado como “1 por cento, sobrescrito 13, subscrito 6, C” e o último é rotulado como “99 por cento, sobrescrito 12, subscrito 6, C.” Duas flechas voltadas para baixo que se fundem em uma flecha conduzem da vaca e da árvore até o chão e são rotuladas como “o organismo morre” e “sobrescrito 14, subscrito 6, C, a decomposição começa”. Uma seta voltada para a direita rotulada na parte superior como “Decaimento” e na parte inferior como “Tempo” leva a uma etiqueta de “sobrescrito 14, subscrito 6, C, barra invertida, sobrescrito 12, subscrito 6, C, proporção diminuída”. Perto do topo da árvore, há uma seta voltada para baixo com o rótulo “sobrescrito 14, subscrito 6, C, barra invertida, sobrescrito 12, subscrito 6, C, a proporção é constante em organismos vivos” que leva à última das afirmações mais baixas.

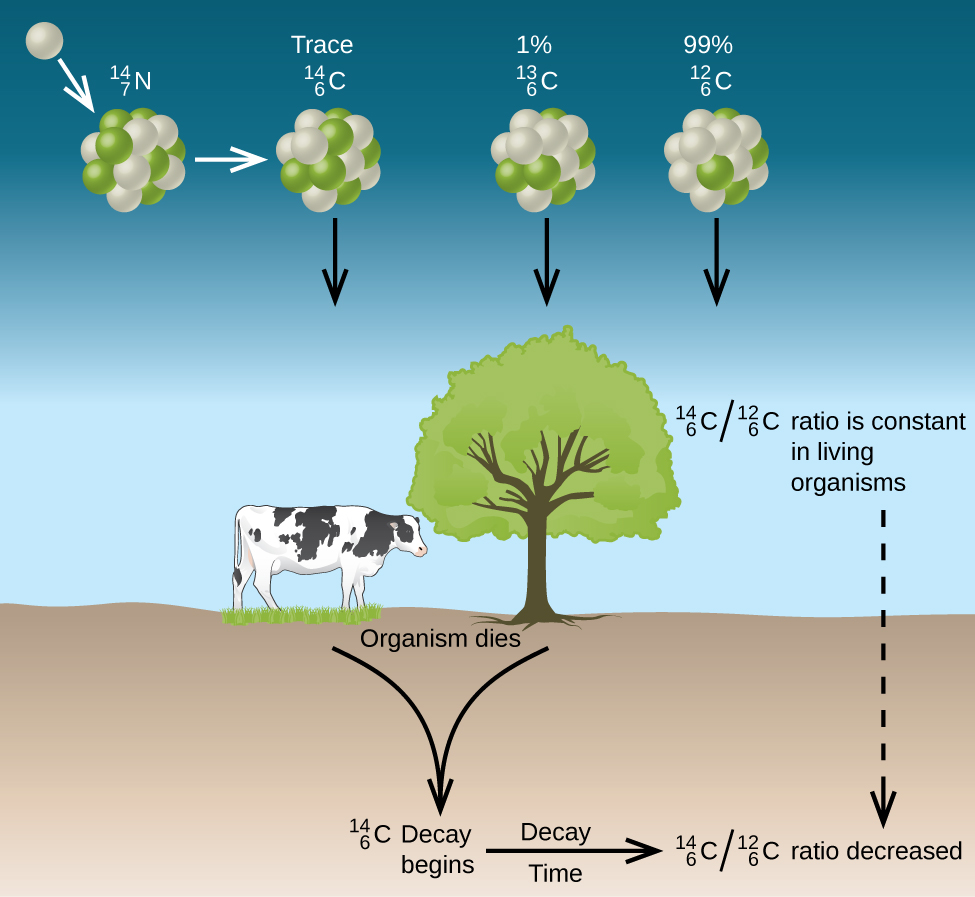
Por exemplo, com a meia-vida de\(\ce{^{14}_6C}\) 5730 anos, se a\(\ce{^{14}_6C : ^{12}_6C}\) proporção em um objeto de madeira encontrado em uma escavação arqueológica for metade da de uma árvore viva, isso indica que o objeto de madeira tem 5730 anos. Determinações de\(\ce{^{14}_6C : ^{12}_6C}\) proporções altamente precisas podem ser obtidas de amostras muito pequenas (tão pouco quanto um miligrama) com o uso de um espectrômetro de massa.

Exemplo\(\PageIndex{2}\): Radiocarbon Dating

Um pequeno pedaço de papel (produzido a partir de matéria vegetal anteriormente viva) retirado dos Manuscritos do Mar Morto tem uma atividade de 10,8 desintegrações por minuto por grama de carbono. Se a atividade inicial do C-14 foi de 13,6 desintegrações/min/g de C, estime a idade dos Manuscritos do Mar Morto.

Solução

A taxa de decaimento (número de desintegrações/minuto/grama de carbono) é proporcional à quantidade de C-14 radioativo restante no papel, então podemos substituir as taxas pelas quantidades, N, na relação:

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)⟶t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right) \nonumber \]

onde o subscrito 0 representa a época em que as plantas foram cortadas para fazer o papel, e o subscrito t representa a hora atual.

A constante de decaimento pode ser determinada a partir da meia-vida de C-14, 5730 anos:

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5730\: y}=1.21×10^{−4}\:y^{−1}} \nonumber \]

Substituindo e resolvendo, temos:

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right)=\mathrm{−\dfrac{1}{1.21×10^{−4}\:y^{−1}}\ln\left(\dfrac{10.8\:dis/min/g\: C}{13.6\:dis/min/g\: C}\right)=1910\: y}\nonumber \]

Portanto, os Manuscritos do Mar Morto têm aproximadamente 1900 anos (Figura\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\): A datação por carbono 14 mostrou que essas páginas dos Manuscritos do Mar Morto foram escritas ou copiadas em papel feito de plantas que morreram entre 100 a.C. e 50 d.C.

Exercício\(\PageIndex{2}\)

Datas mais precisas dos reinados dos antigos faraós egípcios foram determinadas recentemente usando plantas que foram preservadas em seus túmulos. Amostras de sementes e matéria vegetal do túmulo do rei Tutancâmon têm uma taxa de decaimento de C-14 de 9,07 desintegrações/min/g de C. Há quanto tempo o reinado do rei Tut chegou ao fim?

Resposta

cerca de 3350 anos atrás, ou aproximadamente 1340 BC

Houve algumas mudanças significativas e bem documentadas na\(\ce{^{14}_6C : ^{12}_6C}\) proporção. A precisão de uma aplicação direta dessa técnica depende de a\(\ce{^{14}_6C : ^{12}_6C}\) proporção em uma planta viva ser a mesma agora de uma era anterior, mas isso nem sempre é válido. Devido ao crescente acúmulo de moléculas de CO ₂ (em grande parte\(\ce{^{12}_6CO2}\)) na atmosfera causado pela combustão de combustíveis fósseis (nos quais essencialmente todas elas decaíram), a proporção de\(\ce{^{14}_6C : ^{12}_6C}\) na atmosfera pode estar mudando.\(\ce{^{14}_6C}\) Esse aumento causado pelo homem\(\ce{^{12}_6CO2}\) na atmosfera faz com que a\(\ce{^{14}_6C : ^{12}_6C}\) proporção diminua e, por sua vez, afeta a proporção de organismos atualmente vivos na Terra. Felizmente, no entanto, podemos usar outros dados, como datação de árvores por meio do exame de anéis de crescimento anuais, para calcular os fatores de correção. Com esses fatores de correção, datas precisas podem ser determinadas. Em geral, a datação radioativa só funciona por cerca de 10 meias-vidas; portanto, o limite para datação por carbono 14 é de cerca de 57.000 anos.

Datação radioativa usando nuclídeos que não sejam carbono-14

A datação radioativa também pode usar outros nuclídeos radioativos com meia-vida mais longa para datar eventos mais antigos. Por exemplo, o urânio-238 (que decai em uma série de etapas em chumbo-206) pode ser usado para estabelecer a idade das rochas (e a idade aproximada das rochas mais antigas da Terra). Como o U-238 tem meia-vida de 4,5 bilhões de anos, é preciso esse tempo para que metade do U-238 original se decomponha em Pb-206. Em uma amostra de rocha que não contém quantidades apreciáveis de Pb-208, o isótopo de chumbo mais abundante, podemos supor que o chumbo não estava presente quando a rocha foi formada. Portanto, medindo e analisando a proporção de U-238:Pb-206, podemos determinar a idade da rocha. Isso pressupõe que todo o chumbo-206 presente veio da decomposição do urânio-238. Se houver chumbo-206 adicional presente, o que é indicado pela presença de outros isótopos de chumbo na amostra, é necessário fazer um ajuste. A datação por potássio-argônio usa um método semelhante. O K-40 decai por emissão de pósitrons e captura de elétrons para formar o Ar-40 com meia-vida de 1,25 bilhão de anos. Se uma amostra de rocha for triturada e a quantidade de gás Ar-40 que escapa for medida, a determinação da razão Ar-40:K-40 produz a idade da rocha. Outros métodos, como a datação por rubídio-estrôncio (o Rb-87 decai em Sr-87 com meia-vida de 48,8 bilhões de anos), operam segundo o mesmo princípio. Para estimar o limite inferior da idade da Terra, os cientistas determinam a idade de várias rochas e minerais, assumindo que a Terra é mais velha do que as rochas e minerais mais antigos de sua crosta. Em 2014, as rochas mais antigas conhecidas na Terra são os zircões Jack Hills da Austrália, encontrados pela datação de urânio-chumbo com quase 4,4 bilhões de anos.

Exemplo\(\PageIndex{3}\): Radioactive Dating of Rocks

Uma rocha ígnea contém 9,58 × 10 ^—5 g de U-238 e 2,51 × 10 ^—5 g de Pb-206 e quantidades muito, muito menores de Pb-208. Determine o tempo aproximado em que a rocha se formou.

Solução

A amostra de rocha contém muito pouco Pb-208, o isótopo mais comum de chumbo, então podemos supor com segurança que todo o Pb-206 na rocha foi produzido pelo decaimento radioativo do U-238. Quando a rocha se formou, ela continha todo o U-238 atualmente nela, além de alguns U-238 que já sofreram decaimento radioativo.

A quantidade de U-238 atualmente na rocha é:

\[\mathrm{9.58×10^{−5}\cancel{g\: U}×\left( \dfrac{1\: mol\: U}{238\cancel{g\: U}}\right )=4.03×10^{−7}\:mol\: U}\nonumber \]

Porque quando um mol de U-238 decai, ele produz um mol de Pb-206, a quantidade de U-238 que sofreu decaimento radioativo desde que a rocha foi formada é:

\[\mathrm{2.51×10^{-5}\cancel{g\: Pb}×\left( \dfrac{1\cancel{mol\: Pb}}{206\cancel{g\: Pb}}\right )×\left(\dfrac{1\: mol\: U}{1\cancel{mol\: Pb}}\right)=1.22×10^{-7}\:mol\: U}\nonumber \]

A quantidade total de U-238 originalmente presente na rocha é, portanto:

\[\mathrm{4.03×10^{−7}\:mol+1.22×10^{−7}\:mol=5.25×10^{−7}\:mol\: U}\nonumber \]

O tempo decorrido desde a formação da rocha é dado por:

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]

com N ₀ representando a quantidade original de U-238 e N _t representando a quantidade atual de U-238.

O U-238 decai em Pb-206 com meia-vida de 4,5 × 10 ⁹ y, então a constante de decaimento λ é:

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{4.5×10^9\:y}=1.54×10^{−10}\:y^{−1}}\nonumber \]

Substituindo e resolvendo, temos:

\[t=\mathrm{−\dfrac{1}{1.54×10^{−10}\:y^{−1}}\ln\left(\dfrac{4.03×10^{−7}\cancel{mol\: U}}{5.25×10^{−7}\cancel{mol\: U}}\right)=1.7×10^9\:y}\nonumber \]

Portanto, a rocha tem aproximadamente 1,7 bilhão de anos.

Exercício\(\PageIndex{3}\)

Uma amostra de rocha contém 6,14 × 10 ^—4 g de Rb-87 e 3,51 × 10 ^—5 g de Sr-87. Calcule a idade da rocha. (A meia-vida do decaimento β do Rb-87 é 4,7 × 10 ¹⁰ y.)

Resposta

3,7 × 10 ⁹ g

Resumo

Núcleos com relações n:p instáveis sofrem decaimento radioativo espontâneo. Os tipos mais comuns de radioatividade são decaimento α, decaimento β, emissão γ, emissão de pósitrons e captura de elétrons. As reações nucleares também costumam envolver raios γ, e alguns núcleos decaem por captura de elétrons. Cada um desses modos de decaimento leva à formação de um novo núcleo com uma relação n:p mais estável. Algumas substâncias passam por séries de decaimento radioativo, passando por vários decaimentos antes de terminar em um isótopo estável. Todos os processos de decaimento nuclear seguem uma cinética de primeira ordem, e cada radioisótopo tem sua própria meia-vida característica, o tempo necessário para a decomposição da metade de seus átomos. Devido às grandes diferenças de estabilidade entre os nuclídeos, há uma ampla gama de meias-vidas de substâncias radioativas. Muitas dessas substâncias encontraram aplicações úteis no diagnóstico e tratamento médico, determinando a idade de objetos arqueológicos e geológicos e muito mais.

Equações-chave

• taxa de decaimento = λN
• \(t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\)

Glossário

decaimento alfa (α)

perda de uma partícula alfa durante o decaimento radioativo

decaimento beta (β)

quebra de um nêutron em um próton, que permanece no núcleo, e um elétron, que é emitido como uma partícula beta

nuclídeo filha

nuclídeo produzido pela decomposição radioativa de outro nuclídeo; pode ser estável ou pode decair ainda mais

captura de elétrons

combinação de um elétron central com um próton para produzir um nêutron dentro do núcleo

emissão gama (γ)

decaimento de um nuclídeo de estado excitado acompanhado pela emissão de um raio gama

meia-vida (t _1/2)

tempo necessário para que metade dos átomos em uma amostra radioativa se decomponha

nuclídeo parental

nuclídeo instável que se transforma espontaneamente em outro nuclídeo (filho)

emissão de pósitrons

(também, decaimento β ⁺) conversão de um próton em um nêutron, que permanece no núcleo, e um pósitron, que é emitido

decaimento radioativo

decaimento espontâneo de um nuclídeo instável em outro nuclídeo

série de decaimento radioativo

cadeias de desintegrações sucessivas (decaimentos radioativos) que, em última análise, levam a um produto final estável

datação por radiocarbono

meios altamente precisos de datar objetos de 30.000 a 50.000 anos que foram derivados de matéria outrora viva; alcançado calculando a proporção de\(\ce{^{14}_6C : ^{12}_6C}\) no objeto versus a proporção de\(\ce{^{14}_6C : ^{12}_6C}\) na atmosfera atual

datação radiométrica

uso de radioisótopos e suas propriedades para datar a formação de objetos como artefatos arqueológicos, organismos anteriormente vivos ou formações geológicas