21.1: Estrutura e estabilidade nucleares
- Page ID
- 185352
- Descreva a estrutura nuclear em termos de prótons, nêutrons e elétrons
- Calcule o defeito de massa e a energia de ligação dos núcleos
- Explicar as tendências na estabilidade relativa dos núcleos
A química nuclear é o estudo de reações que envolvem mudanças na estrutura nuclear. O capítulo sobre átomos, moléculas e íons introduziu a ideia básica da estrutura nuclear, de que o núcleo de um átomo é composto por prótons e, com exceção de\(\ce{^1_1H}\), nêutrons. Lembre-se de que o número de prótons no núcleo é chamado de número atômico (\(Z\)) do elemento, e a soma do número de prótons e do número de nêutrons é o número de massa (\(A\)). Átomos com o mesmo número atômico, mas números de massa diferentes, são isótopos do mesmo elemento. Quando nos referimos a um único tipo de núcleo, costumamos usar o termo nuclídeo e identificá-lo pela notação:
\[\ce{^{A}_{Z}X} \label{Eq1} \]
onde
- \(X\)é o símbolo do elemento,
- \(A\)é o número da massa e
- \(Z\)é o número atômico.
Freqüentemente, um nuclídeo é referenciado pelo nome do elemento seguido por um hífen e pelo número da massa. Por exemplo,\(\ce{^{14}_6C}\) é chamado de “carbono-14".
Prótons e nêutrons, chamados coletivamente de nucleons, são agrupados firmemente em um núcleo. Com um raio de cerca de 10 a 15 metros, um núcleo é bem pequeno em comparação com o raio de todo o átomo, que é de cerca de 10 a 10 metros. Os núcleos são extremamente densos em comparação com a matéria a granel, com média de\(1.8 \times 10^{14}\) gramas por centímetro cúbico. Por exemplo, a água tem uma densidade de 1 grama por centímetro cúbico e o irídio, um dos elementos mais densos conhecidos, tem uma densidade de 22,6 g/cm 3. Se a densidade da Terra fosse igual à densidade nuclear média, o raio da Terra seria de apenas cerca de 200 metros (o raio real da Terra é de aproximadamente\(6.4 \times 10^6\) metros, 30.000 vezes maior). O exemplo\(\PageIndex{1}\) demonstra o quão grandes as densidades nucleares podem ser no mundo natural.
Densidade de uma estrela de nêutrons As estrelas de nêutrons se formam quando o núcleo de uma estrela muito massiva sofre um colapso gravitacional, fazendo com que as camadas externas da estrela explodam em uma supernova. Compostas quase completamente por nêutrons, elas são as estrelas mais densas conhecidas no universo, com densidades comparáveis à densidade média de um núcleo atômico. Uma estrela de nêutrons em uma galáxia distante tem uma massa igual a 2,4 massas solares (1 massa solar\(M_☉\) = = massa do sol =\(\mathrm{1.99 \times 10^{30}\; kg}\)) e um diâmetro de 26 km.
- Qual é a densidade\(\rho\) dessa estrela de nêutrons?
- Como a densidade dessa estrela de nêutrons se compara à densidade de um núcleo de urânio, que tem um diâmetro de cerca de 15 fm (1 fm = 10 —15 m)?
Solução
Podemos tratar tanto a estrela de nêutrons quanto o núcleo U-235 como esferas. Então, a densidade para ambos é dada por:
\[\rho = \dfrac{m}{V} \nonumber \]
com
\[V = \dfrac{4}{3} \pi r^3 \nonumber \]
(a) O raio da estrela de nêutrons é\(\mathrm{\dfrac{1}{2}\times 26\; km = \dfrac{1}{2} \times 2.6 \times 10^4\; m = 1.3 \times 10^4\; m}\) então que a densidade da estrela de nêutrons é:
\[ \begin{align*} \rho &= \dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{2.4(1.99 \times 10^{30}\;kg)}{\frac{4}{3} \pi (1.3 \times 10^4m)^3} \\[4pt] &=5.2 \times 10^{17}\;kg/m^3 \end{align*} \nonumber \]
(b) O raio do núcleo U-235 é\(\mathrm{\dfrac{1}{2} \times 15 \times 10^{−15}\;m=7.5 \times 10^{−15}\;m}\), então a densidade do núcleo U-235 é:
\[ \begin{align*} \rho &=\dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{235\;amu \left(\frac{1.66 \times 10^{-27}\;kg}{1\;amu}\right)}{ \frac{4}{3} \pi (7.5 \times 10^{-15}m)^3} \\[4pt] &=2.2 \times 10^{17} \; kg/m^3 \end{align*} \nonumber \]
Esses valores são bastante semelhantes (mesma ordem de magnitude), mas o núcleo é duas vezes mais denso que a estrela de nêutrons.
Encontre a densidade de uma estrela de nêutrons com uma massa de 1,97 massas solares e um diâmetro de 13 km e compare-a com a densidade de um núcleo de hidrogênio, que tem um diâmetro de 1,75 fm (\(\mathrm{1\; fm = 1 \times 10^{–15}\; m}\)).
- Responda
-
A densidade da estrela de nêutrons é\(\mathrm{3.4 \times 10^{18}\; kg/m^3}\). A densidade de um núcleo de hidrogênio é\(\mathrm{6.0 \times 10^{17}\; kg/m^3}\). A estrela de nêutrons é 5,7 vezes mais densa que o núcleo de hidrogênio.
Manter prótons carregados positivamente juntos no volume muito pequeno de um núcleo requer forças de atração muito fortes porque os prótons carregados positivamente se repelem fortemente a distâncias tão curtas. A força de atração que mantém o núcleo unido é a força nuclear forte. (A força forte é uma das quatro forças fundamentais que se sabe que existem. As outras são a força eletromagnética, a força gravitacional e a força nuclear fraca.) Essa força atua entre prótons, entre nêutrons e entre prótons e nêutrons. É muito diferente da força eletrostática que mantém elétrons carregados negativamente em torno de um núcleo com carga positiva (a atração entre cargas opostas). Em distâncias inferiores a 10-15 metros e dentro do núcleo, a força nuclear forte é muito mais forte do que as repulsões eletrostáticas entre prótons; em distâncias maiores e fora do núcleo, ela é essencialmente inexistente.
Energia de ligação nuclear
Como um exemplo simples da energia associada à força nuclear forte, considere o átomo de hélio composto por dois prótons, dois nêutrons e dois elétrons. A massa total dessas seis partículas subatômicas pode ser calculada como:
\[ \underset{\Large\text{protons}}{(2 \times 1.0073\; \text{amu})} + \underset{\Large\text{neutrons}}{(2 \times 1.0087\; \text{amu})} + \underset{\Large\text{electrons}}{(2 \times 0.00055\; \text{amu})}= 4.0331\; \text{amu }\label{Eq2} \]
No entanto, medições espectrométricas de massa revelam que a massa de um\(\ce{_2^4 He}\) átomo é 4.0026 amu, menor do que as massas combinadas de suas seis partículas subatômicas constituintes. Essa diferença entre as massas calculadas e medidas experimentalmente é conhecida como defeito de massa do átomo. No caso do hélio, o defeito de massa indica uma “perda” de massa de 4,0331 amu — 4,0026 amu = 0,0305 amu. A perda de massa que acompanha a formação de um átomo a partir de prótons, nêutrons e elétrons se deve à conversão dessa massa em energia que evolui à medida que o átomo se forma. A energia de ligação nuclear é a energia produzida quando os núcleons dos átomos estão unidos; essa também é a energia necessária para quebrar um núcleo em seus prótons e nêutrons constituintes. Em comparação com as energias de ligação química, as energias de ligação nuclear são muito maiores, como aprenderemos nesta seção. Consequentemente, as mudanças de energia associadas às reações nucleares são muito maiores do que as das reações químicas.
A conversão entre massa e energia é representada de forma mais identificável pela equação de equivalência massa-energia, conforme declarado por Albert Einstein:
\[E=mc^2 \label{Eq3} \]
onde E é energia, m é a massa da matéria sendo convertida e c é a velocidade da luz no vácuo. Essa equação pode ser usada para encontrar a quantidade de energia que resulta quando a matéria é convertida em energia. Usando essa equação de equivalência massa-energia, a energia de ligação nuclear de um núcleo pode ser calculada a partir de seu defeito de massa, conforme demonstrado em Exemplo\(\PageIndex{2}\). Uma variedade de unidades é comumente usada para energias de ligação nuclear, incluindo elétron-volts (eV), com 1 eV igual à quantidade de energia necessária para mover a carga de um elétron através de uma diferença de potencial elétrico de 1 volt, fazendo\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\).
Determine a energia de ligação para o nuclídeo\(\ce{^4_2 He}\) em:
- joules por mol de núcleos
- joules por núcleo
- MeV por núcleo
Solução
O defeito de massa de um\(\ce{^4_2He}\) núcleo é 0,0305 amu, conforme mostrado anteriormente. Determine a energia de ligação em joules por nuclídeo usando a equação de equivalência massa-energia. Para acomodar as unidades de energia solicitadas, o defeito de massa deve ser expresso em quilogramas (lembre-se de que 1 J = 1 kg m 2 /s 2).
(a) Primeiro, expresse o defeito de massa em g/mol. Isso é feito facilmente considerando a equivalência numérica da massa atômica (amu) e da massa molar (g/mol) que resulta das definições das unidades amu e mol (consulte a discussão anterior no capítulo sobre átomos, moléculas e íons, se necessário). O defeito de massa é, portanto, 0,0305 g/mol. Para acomodar as unidades dos outros termos na equação massa-energia, a massa deve ser expressa em kg, já que 1 J = 1 kg m 2 /s 2. A conversão de gramas em quilogramas produz um defeito de massa de\(\mathrm{3.05 \times 10^{–5}\; kg/mol}\). Substituir essa quantidade na equação de equivalência massa-energia produz:
\[\begin{align*} E &=mc^2 \\[4pt] &= \dfrac{3.05 \times 10^{-5}\;kg}{mol} \times \left(\dfrac{2.998 \times 10^8\;m}{s}\right)^2 \\[4pt] &= 2.74×10^{12}\:kg\:m^2s^{-2}mol^{-1} \\[4pt] &=2.74 \times 10^{12}\;J/mol=2.74\: TJ /mol \end{align*} \nonumber \]
(b) A energia de ligação para um único núcleo é calculada a partir da energia de ligação molar usando o número de Avogadro:
\[\begin{align*} E &= 2.74×10^{12}\:J\:mol^{-1}×\dfrac{1\: mol}{6.022×10^{23}\:nuclei} \\[4pt] &=4.55×10^{-12} \: J =4.55\: pJ \end{align*} \nonumber \]
(c) Lembre-se disso\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\). Usando a energia de ligação calculada na parte (b):
\[\begin{align*} E &= 4.55×10^{-12} \: J× \dfrac{1\: eV}{1.602×10^{-19}\:J} \\[4pt] &=2.84×10^7\:eV=28.4\: MeV \end{align*} \nonumber \]
Qual é a energia de ligação do nuclídeo\(\ce{^{19}_9F}\) (massa atômica: 18,9984 amu) em MeV por núcleo?
- Responda
-
148,4 MeV
Como as mudanças de energia para quebrar e formar ligações são muito pequenas em comparação com as mudanças de energia para quebrar ou formar núcleos, as mudanças na massa durante todas as reações químicas comuns são praticamente indetectáveis. Conforme descrito no capítulo sobre termoquímica, as reações químicas mais energéticas exibem entalpias da ordem de milhares de kJ/mol, o que equivale às diferenças de massa na faixa de nanogramas (10 a 9 g). Por outro lado, as energias de ligação nuclear são tipicamente da ordem de bilhões de kJ/mol, correspondendo a diferenças de massa na faixa de miligramas (10 —3 g).
Estabilidade nuclear
Um núcleo é estável se não puder ser transformado em outra configuração sem adicionar energia externa. Dos milhares de nuclídeos existentes, cerca de 250 são estáveis. Um gráfico do número de nêutrons versus o número de prótons para núcleos estáveis revela que os isótopos estáveis caem em uma banda estreita. Essa região é conhecida como faixa de estabilidade (também chamada de cinturão, zona ou vale da estabilidade). A linha reta na Figura\(\PageIndex{1}\) representa núcleos que têm uma proporção 1:1 de prótons para nêutrons (razão n:p). Observe que os núcleos estáveis mais leves, em geral, têm números iguais de prótons e nêutrons. Por exemplo, o nitrogênio-14 tem sete prótons e sete nêutrons. Núcleos estáveis mais pesados, no entanto, têm cada vez mais nêutrons do que prótons. Por exemplo: o ferro-56 tem 30 nêutrons e 26 prótons, uma razão n:p de 1,15, enquanto o nuclídeo estável chumbo-207 tem 125 nêutrons e 82 prótons, uma razão n:p igual a 1,52. Isso ocorre porque núcleos maiores têm mais repulsões próton-próton e exigem um número maior de nêutrons para fornecer forças compensadoras fortes para superar essas repulsões eletrostáticas e manter o núcleo unido.
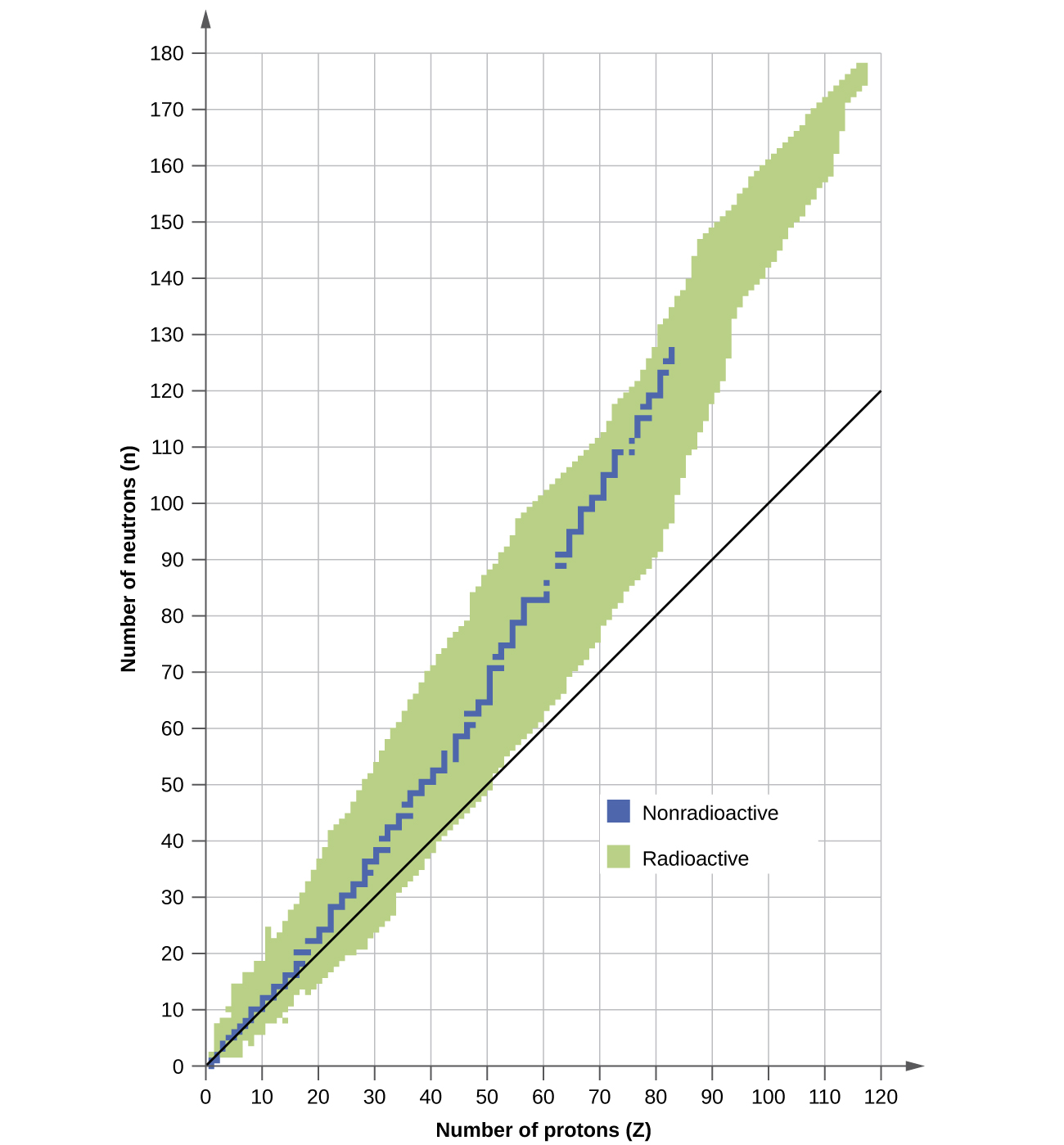
Os núcleos que estão à esquerda ou à direita da faixa de estabilidade são instáveis e exibem radioatividade. Eles se transformam espontaneamente (decaem) em outros núcleos que estão dentro ou mais próximos da faixa de estabilidade. Essas reações de decaimento nuclear convertem um isótopo instável (ou radioisótopo) em outro isótopo mais estável. Discutiremos a natureza e os produtos desse decaimento radioativo nas seções subsequentes deste capítulo.
Várias observações podem ser feitas sobre a relação entre a estabilidade de um núcleo e sua estrutura. Núcleos com números pares de prótons, nêutrons ou ambos têm maior probabilidade de serem estáveis (Tabela\(\PageIndex{1}\)). Núcleos com certos números de nucleons, conhecidos como números mágicos, são estáveis contra o decaimento nuclear. Esses números de prótons ou nêutrons (2, 8, 20, 28, 50, 82 e 126) formam camadas completas no núcleo. Eles são semelhantes em conceito às camadas de elétrons estáveis observadas para os gases nobres. Núcleos que têm números mágicos de prótons e nêutrons, como\(\ce{^4_2He}\),\(\ce{^{16}_8O}\)\(\ce{^{40}_{20}Ca}\), e\(\ce{^{208}_{82}Pb}\) e são particularmente estáveis. Essas tendências na estabilidade nuclear podem ser racionalizadas considerando um modelo de mecânica quântica de estados de energia nuclear análogo ao usado para descrever estados eletrônicos anteriormente neste livro didático. Os detalhes desse modelo estão além do escopo deste capítulo.
| Número de isótopos estáveis | Número de prótons | Número de nêutrons |
|---|---|---|
| 157 | uniforme | uniforme |
| 53 | uniforme | estranha |
| 50 | estranha | uniforme |
| 5 | estranha | estranha |
A estabilidade relativa de um núcleo está correlacionada com sua energia de ligação por núcleo, a energia total de ligação para o núcleo dividida pelo número ou núcleons no núcleo. Por exemplo, a energia de ligação para um\(\ce{^4_2He}\) núcleo é, portanto:
\[\mathrm{\dfrac{28.4\; MeV}{4\; nucleons}=7.10\; MeV/nucleon} \label{Eq3a} \]
A energia de ligação por núcleo de um nuclídeo na curva mostrada na Figura\(\PageIndex{2}\)
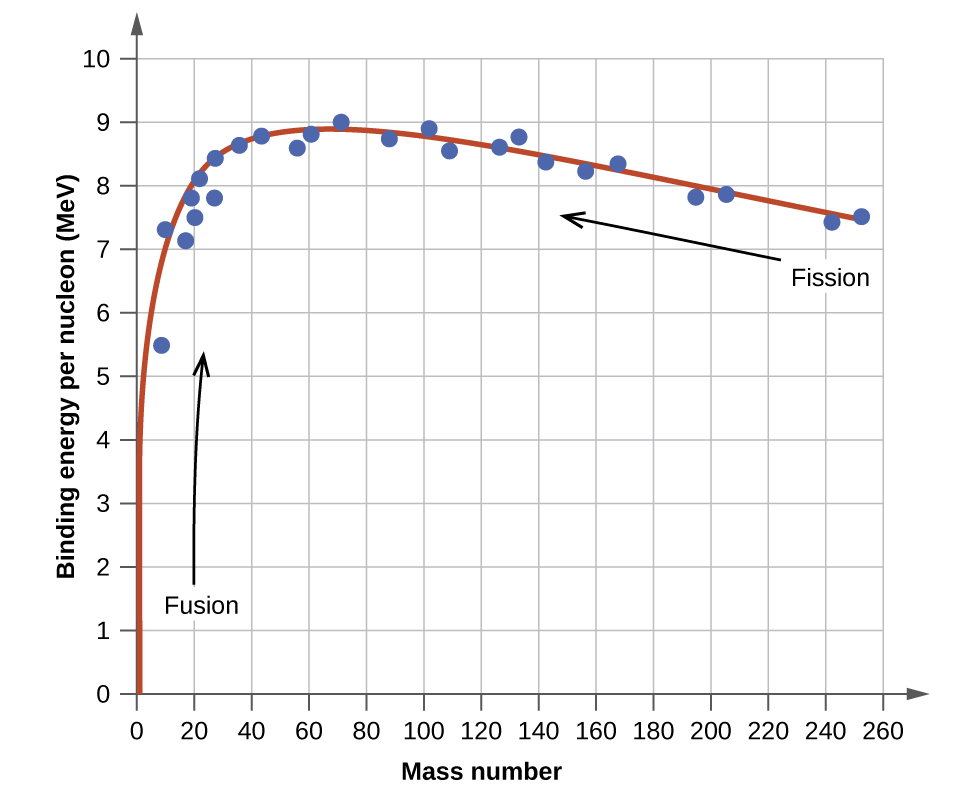
O nuclídeo de ferro\(\ce{^{56}_{26}Fe}\) fica próximo ao topo da curva de energia de ligação (Figura\(\PageIndex{2}\)) e é um dos nuclídeos mais estáveis. Qual é a energia de ligação por núcleo (em MeV) para o nuclídeo\(\ce{^{56}_{26}Fe}\) (massa atômica de 55,9349 amu)?
Solução
Como no exemplo, primeiro determinamos o defeito de massa do nuclídeo, que é a diferença entre a massa de 26 prótons, 30 nêutrons e 26 elétrons, e a massa observada de um\(\ce{^{56}_{26}Fe}\) átomo:
\ [\ begin {align*}
\ mathrm {Massa\: defeito} &=\ mathrm {[(26×1.0073\: amu) + (30×1.0087\: amu) + (26×0,00055\: amu)] −55.9349\: amu}\\
&=\ mathrm {56.4651\: amu−55.9349\: amu}\\ &=\ mathrm {56.4651\: amu 349\: amu}\\
&=\ mathrm {0,5302\: amu}
\ end {align*}\ nonumber\]
Em seguida, calculamos a energia de ligação para um núcleo a partir do defeito de massa usando a equação de equivalência massa-energia:
\ [\ begin {align*}
E&=mc^2=\ mathrm {0,5302\: amu×\ dfrac {1.6605×10^ {-27}\ :kg} {1\: amu} × (2,998×10^8\ :m/s) ^2}\\
&=\ mathrm {7,913×10^ {−11}\: trm {kg⋅m} /s^2}\\
&=\ mathrm {7,913×10^ {−11}\ :J}
\ end {align*}\ nonumber\]
Em seguida, convertemos a energia de ligação em joules por núcleo em unidades de MeV por nuclídeo:
\[\mathrm{7.913×10^{−11}\:J×\dfrac{1\: MeV}{1.602×10^{−13}\:J}=493.9\: MeV} \nonumber \]
Finalmente, determinamos a energia de ligação por núcleo dividindo a energia total de ligação nuclear pelo número de nucleons no átomo:
\[\textrm{Binding energy per nucleon}=\mathrm{\dfrac{493.9\: MeV}{56}=8.820\: MeV/nucleon} \nonumber \]
Observe que isso é quase 25% maior do que a energia de ligação por núcleo para\(\ce{^4_2He}\). (Observe também que esse é o mesmo processo do Example\ (\ PageIndex {2}\, mas com a etapa adicional de dividir a energia total de ligação nuclear pelo número de nucleons.)
Qual é a energia de ligação por núcleo em\(\ce{^{19}_9F}\) (massa atômica, 18.9984 amu)?
- Responda
-
7.810 MeV/nucleon
Resumo
Um núcleo atômico consiste em prótons e nêutrons, chamados coletivamente de nucleons. Embora os prótons se repelam, o núcleo é mantido firmemente unido por uma força de curto alcance, mas muito forte, chamada força nuclear forte. Um núcleo tem menos massa do que a massa total de seus núcleons constituintes. Essa massa “ausente” é o defeito de massa, que foi convertido na energia de ligação que mantém o núcleo unido de acordo com a equação de equivalência massa-energia de Einstein, E = mc 2. Dos muitos nuclídeos existentes, apenas um pequeno número é estável. Nuclídeos com números pares de prótons ou nêutrons, ou aqueles com números mágicos de nucleons, são especialmente propensos a serem estáveis. Esses nuclídeos estáveis ocupam uma faixa estreita de estabilidade em um gráfico do número de prótons versus número de nêutrons. A energia de ligação por núcleo é maior para os elementos com números de massa próximos a 56; esses são os núcleos mais estáveis.
Equações-chave
- E = cm 2
Glossário
- faixa de estabilidade
- (também, cinturão de estabilidade, zona de estabilidade ou vale de estabilidade) região do gráfico do número de prótons versus número de nêutrons contendo nuclídeos estáveis (não radioativos)
- energia de ligação por núcleo
- energia de ligação total para o núcleo dividida pelo número de nucleons no núcleo
- voltagem eletrônica (eV)
- unidade de medição de energias de ligação nuclear, com 1 eV igual à quantidade de energia devido à movimentação de um elétron através de uma diferença de potencial elétrico de 1 volt
- número mágico
- núcleos com números específicos de nucleons que estão dentro da faixa de estabilidade
- defeito de massa
- diferença entre a massa de um átomo e a massa somada de suas partículas subatômicas constituintes (ou a massa “perdida” quando os nucleons são reunidos para formar um núcleo)
- equação de equivalência massa-energia
- A relação de Albert Einstein mostrando que massa e energia são equivalentes
- energia de ligação nuclear
- energia perdida quando os nucleons de um átomo são unidos (ou a energia necessária para quebrar um núcleo em seus prótons e nêutrons constituintes)
- química nuclear
- estudo da estrutura dos núcleos atômicos e processos que alteram a estrutura nuclear
- nucléon
- termo coletivo para prótons e nêutrons em um núcleo
- nuclídeo
- núcleo de um isótopo específico
- radioatividade
- fenômeno exibido por um nucleon instável que se transforma espontaneamente em um nucleon que é mais estável; diz-se que um nucleon instável é radioativo
- radioisótopo
- isótopo que é instável e sofre conversão em um isótopo diferente e mais estável
- força nuclear forte
- força de atração entre nucleons que mantém um núcleo unido


