17.4: A equação de Nernst
- Page ID
- 184749
- Relacione os potenciais celulares às mudanças de energia livre
- Use a equação de Nernst para determinar os potenciais celulares em condições não padronizadas
- Execute cálculos que envolvam a conversão entre potenciais celulares, mudanças de energia livre e constantes de equilíbrio
Agora estenderemos a eletroquímica determinando a relação entre\(E^\circ_\ce{cell}\) e as quantidades termodinâmicas, como ΔG° (energia livre de Gibbs) e K (a constante de equilíbrio). Nas células galvânicas, a energia química é convertida em energia elétrica, que pode funcionar. O trabalho elétrico é o produto da carga transferida multiplicada pela diferença de potencial (tensão):
\[\mathrm{electrical\: work=volts \times (charge\: in\: coulombs)=J} \nonumber \]
A carga em 1 mol de elétrons é dada pela constante de Faraday (F)
\[ \begin{align*} F &=\dfrac{6.022 \times 10^{23}\:e^-}{mol} \times \dfrac{1.602 \times 10^{−19}\:C}{e^-} \\[4pt] &=9.648 \times 10^4\:\dfrac{C}{mol} \\[4pt] &=9.648 \times 10^4\:\dfrac{J}{V⋅mol} \end{align*} \nonumber \]
Portanto
\[\mathrm{total\: charge=(number\: of\: moles\: of\: e^-)} \times F=nF \nonumber \]
Nesta equação,\(n\) é o número de moles de elétrons para a reação balanceada de oxidação-redução. O potencial celular medido é o potencial máximo que a célula pode produzir e está relacionado ao trabalho elétrico (w ele) por
\[E_\ce{cell}=\dfrac{−w_\ce{ele}}{nF}\hspace{40px}\ce{or}\hspace{40px}w_\ce{ele}=−nFE_\ce{cell} \nonumber \]
O sinal negativo do trabalho indica que o trabalho elétrico é feito pelo sistema (a célula galvânica) no entorno. Em um capítulo anterior, a energia livre foi definida como a energia que estava disponível para trabalhar. Em particular, a mudança na energia livre foi definida em termos do trabalho máximo (\(w_{max}\)), que, para sistemas eletroquímicos, é\(w_{ele}\).
\[\begin{align*} ΔG&=w_\ce{max}=w_\ce{ele} \\[4pt] &=−nFE_\ce{cell} \end{align*} \nonumber \]
Podemos verificar se os sinais estão corretos quando percebemos que\(n\)\(F\) são constantes positivas e que as células galvânicas, que têm potenciais celulares positivos, envolvem reações espontâneas. Assim, as reações espontâneas, que têm\(ΔG < 0\), devem ter\(E_{cell} > 0\). Se todos os reagentes e produtos estiverem em seus estados padrão, isso se torna
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
Isso fornece uma maneira de relacionar os potenciais celulares padrão às constantes de equilíbrio, uma vez que
\[ΔG°=−RT\ln K \nonumber \]
\[−nFE^\circ_\ce{cell}=−RT\ln K \nonumber \]
ou
\[ E^\circ_\ce{cell}=\dfrac{RT}{nF}\ln K \nonumber \]
Na maioria das vezes, as reações eletroquímicas são executadas na temperatura padrão (298,15 K). A coleta de termos nessa temperatura produz
\[\begin{align*} E^\circ_\ce{cell}&=\dfrac{RT}{nF}\:\ln K \\[4pt] &=\dfrac{\left(8.314\:\dfrac{\ce{J}}{\textrm{K⋅mol}}\right)(298.15\:K)}{n \times 96,485\: \textrm{C/V⋅mol}}\:\ln K \\[4pt] &=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K \end{align*} \nonumber \]
onde\(n\) está o número de moles de elétrons. O logaritmo em equações envolvendo potenciais celulares é frequentemente expresso usando logaritmos de base 10 (ou seja,\(\log_{10}\) ou apenas\(\log\)), que alteram a constante por um fator de 2,303:
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
Assim, se ΔG°, K ou\(E^\circ_\ce{cell}\) for conhecido ou puder ser calculado, as outras duas quantidades podem ser facilmente determinadas. As relações são mostradas graficamente na Figura\(\PageIndex{1}\).
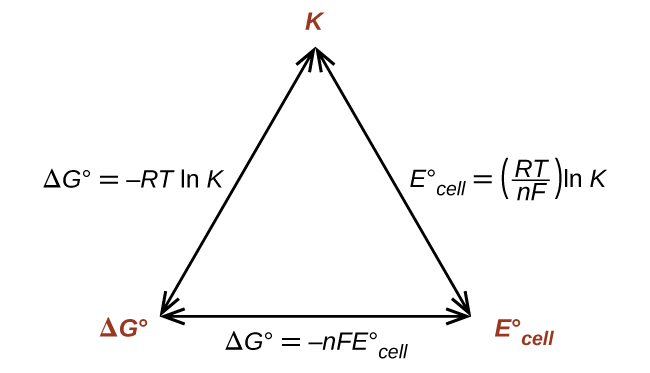
Dada qualquer uma das quantidades, as outras duas podem ser calculadas.
Qual é a mudança de energia livre padrão de Gibbs e a constante de equilíbrio para a seguinte reação a 25 °C?
\[\ce{2Ag+}(aq)+\ce{Fe}(s)⇌\ce{2Ag}(s)+\ce{Fe^2+}(aq) \nonumber \]
Então, lução
A reação envolve uma reação de redução de oxidação, portanto, o potencial celular padrão pode ser calculado usando os dados na Tabela P1.
\ [\ begin {align*}
&\ textrm {ânodo (oxidação):}\ ce {Fe} (s) ⟶\ ce {Fe^2+} (aq) +\ ce {2e-}\ hspace {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0,447\: V}\ nonumber\
&\ textrm {cátodo (redução):} 2\ times (\ ce {Ag+} (aq) +\ ce {e-} ⟶\ ce {Ag} (s))\ hspace {40px} E^\ circ_ {\ ce {Ag+/Ag}} =\ mathrm {0,7996\ : V}\ nonumber\\
&E^\ circ_\ ce {célula} =E^\ circ_\ ce {cátodo} −E^\ circ_\ ce {ânodo} =E^\ circ_ {\ ce {Ag+/Ag}} −E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {+1.247\: V}\ nonum ber
\ end {align*}\ nonumber\]
Lembre-se de que o potencial celular do cátodo não é multiplicado por dois ao determinar o potencial celular padrão. Com n = 2, a constante de equilíbrio é então
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
\[\begin{align*} K&=10^{n \times E^\circ_\ce{cell}/\mathrm{0.0592\: V}} \\[4pt] &=10^{2 \times \mathrm{1.247\: V/0.0592\: V}} \\[4pt] &=10^{42.128} \\[4pt] &=1.3 \times 10^{42}\end{align*} \nonumber \]
A energia livre padrão é então
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
\[ΔG°=\mathrm{−2 \times 96,485\:\dfrac{J}{\textrm{V⋅mol}} \times 1.247\: V=−240.6\:\dfrac{kJ}{mol}} \nonumber \]
Verifique sua resposta: Um potencial celular padrão positivo significa uma reação espontânea, então a mudança padrão de energia livre deve ser negativa e uma constante de equilíbrio deve ser >1.
Qual é a mudança de energia livre padrão de Gibbs e a constante de equilíbrio para a seguinte reação à temperatura ambiente? A reação é espontânea?
\[\ce{Sn}(s)+\ce{2Cu^2+}(aq)⇌\ce{Sn^2+}(aq)+\ce{2Cu+}(aq) \nonumber \]
- Resposta
-
Espontâneo; n = 2;\(E^\circ_\ce{cell}=\mathrm{+0.291\: V}\);\(ΔG°=\mathrm{−56.2\:\dfrac{kJ}{mol}}\);\(K = 6.8 \times 10^9\).
Agora que a conexão foi feita entre a energia livre e os potenciais celulares, seguem concentrações não padronizadas. Lembre-se de que
\[ΔG=ΔG°+RT\ln Q \nonumber \]
onde\(Q\) está o quociente de reação (veja o capítulo sobre os fundamentos do equilíbrio). Conversão para potenciais celulares:
\[−nFE_\ce{cell}=−nFE^\circ_\ce{cell}+RT\ln Q \label{nernst1A} \]
ou
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \label{nernst1B} \]
A equação\ ref {nernst1b} é a equação generalizada de Nernst que é aplicável a qualquer temperatura. No entanto, pode ser simplificado para reações que ocorrem a 25 °C (298,15 K) reescrevendo-o como
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0257\: V}}{n}\:\ln Q \label{nernst2A} \]
ou
\[ E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\log_{10} Q \label{nernst2B} \]
Se a temperatura não for 298,15 K, é necessário recalcular o potencial com a Equação\ ref {Nernst1b}. Com a equação de Nernst, é possível calcular o potencial celular em condições não padronizadas. Esse ajuste é necessário porque os potenciais determinados sob condições diferentes terão valores diferentes.
Considere a seguinte reação à temperatura ambiente:
\[\ce{Co}(s)+\ce{Fe^2+}(aq,\:1.94\:M)⟶\ce{Co^2+}(aq,\: 0.15\:M)+\ce{Fe}(s) \nonumber \]
O processo é espontâneo?
Solução
Há duas maneiras de resolver o problema. Se as informações termodinâmicas na Tabela T1 estivessem disponíveis, você poderia calcular a mudança de energia livre. Se a mudança de energia livre for negativa, o processo é espontâneo. A outra abordagem, que usaremos, requer informações como as fornecidas na Tabela P1. Usando esses dados, o potencial celular pode ser determinado. Se o potencial celular for positivo, o processo é espontâneo. Coletando informações da Tabela P1 e o problema,
\ [\ begin {align*}
&\ textrm {Ânodo (oxidação):}\ ce {Co} (s) ⟶\ ce {Co^2+} (aq) +\ ce {2e-}\ hspace {40px} E^\ circ_ {\ ce {Co^2+/Co}} =\ mathrm {−0,28\: V}\\
&\ textrm {Cátodo (redução):}\ ce {Fe^2+} (aq) +\ ce {2e-} ⟶\ ce {Fe} (s)\ hspace {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0,447\: V}\\
&E^\ circ_\ ce {cell} =E^\ circ_\ ce {cátodo} −E^\ circ_\ ce {ânodo} =\ mathrm {−0,447\: V − (−0,28\: V) =−0,17\: V}
\ end {align*}\ nonumber\]
O processo não é espontâneo em condições padrão. Usando a equação de Nernst e as concentrações declaradas no problema e\(n = 2\),
\[Q=\ce{\dfrac{[Co^2+]}{[Fe^2+]}}=\dfrac{0.15\:M}{1.94\:M}=0.077 \nonumber \]
Agora podemos inseri-los na Equação de Nernst à temperatura ambiente (Equação\ ref {Nernst2b})
\[\begin{align*} E_\ce{cell} &=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \\[4pt] &=\mathrm{−0.17\: V−\dfrac{0.0592\: V}{2}\:\log 0.077} \\[4pt] &=\mathrm{−0.17\: V+0.033\: V=−0.14\: V} \end{align*} \nonumber \]
O processo é (ainda) não espontâneo.
Qual é o potencial celular para a seguinte reação em temperatura ambiente?
\[\ce{Al}(s)│\ce{Al^3+}(aq,\:0.15\:M)║\ce{Cu^2+}(aq,\:0.025\:M)│\ce{Cu}(s) \nonumber \]
Quais são os valores de n e Q para a reação geral? A reação é espontânea nessas condições?
- Resposta
-
n = 6; Q = 1440; célula E = +1,97 V, espontânea.
Finalmente, daremos uma breve olhada em um tipo especial de célula chamada célula de concentração. Em uma célula de concentração, os eletrodos são do mesmo material e as meias-células diferem apenas na concentração. Como um ou ambos os compartimentos não são padrão, os potenciais celulares serão desiguais; portanto, haverá uma diferença de potencial, que pode ser determinada com o auxílio da equação de Nernst.
Qual é o potencial celular da célula de concentração descrito por
\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\: 0.10\:M)║\ce{Zn^2+}(aq,\: 0.50\:M)│\ce{Zn}(s) \nonumber \]
Então, lução
A partir das informações fornecidas:
\ [\ begin {align*}
&\ textrm {Ânodo:}\ ce {Zn} (s) ⟶\ ce {Zn^2+} (aq,\: 0,10\ :M) +\ ce {2e-}\ hspace {40px} E^\ circ_\ ce {ânodo} =\ mathrm {−0,7618\: V}\\ &\ textrm {−0,7618\: V}\\
&\ textrm m {Cátodo:}\ ce {Zn^2+} (aq,\: 0,50\ :M) +\ ce {2e-} ⟶\ ce {Zn} (s)\ hspace {40px} E^\ circ_\ ce {cátodo} =\ mathrm {−0,7618\: V}\\
& amp;\ overline {\ textrm {Geral:}\ ce {Zn^2+} (aq,\: 0,50\ :M) ⟶\ ce {Zn^2+} (aq,\: 0,10\ :M)\ hspace {40px} E^\ circ_\ ce {cell} =\ mathrm {0.000\: V}}
\ end {align*}\ nonumber\]
O potencial celular padrão é zero porque o ânodo e o cátodo envolvem a mesma reação; somente a concentração de Zn 2 + muda. Substituindo na equação de Nernst,
\[E_\ce{cell}=\mathrm{0.000\: V−\dfrac{0.0592\: V}{2}\:\log\dfrac{0.10}{0.50}=+0.021\: V} \nonumber \]
e o processo é espontâneo nessas condições.
Verifique sua resposta: Em uma célula de concentração, o potencial celular padrão sempre será zero. Para obter um potencial celular positivo (processo espontâneo), o quociente de reação Q deve ser <1. Q < 1 nesse caso, então o processo é espontâneo.
Qual valor de Q para a célula de concentração anterior resultaria em uma tensão de 0,10 V? Se a concentração de íon zinco no cátodo fosse de 0,50 M, qual era a concentração no ânodo?
- Resposta
-
Q = 0,00042; [Zn 2 +] cat = 2,1\ vezes 10 −4 M.
Resumo
O trabalho elétrico (w ele) é o negativo do produto da carga total (Q) e do potencial da célula (célula E). A carga total pode ser calculada como o número de moles de elétrons (n) vezes a constante de Faraday (F = 96.485 C/mol e −). O trabalho elétrico é o trabalho máximo que o sistema pode produzir e, portanto, é igual à mudança na energia livre. Assim, qualquer coisa que possa ser feita com ou para uma mudança de energia livre também pode ser feita para ou com um potencial celular. A equação de Nernst relaciona o potencial celular em condições não padronizadas com o logaritmo do quociente de reação. As células de concentração exploram essa relação e produzem um potencial celular positivo usando meias-células que diferem apenas na concentração de seus solutos.
Equações-chave
- \(E^\circ_\ce{cell}=\dfrac{RT}{nF}\:\ln K\)
- \(E^\circ_\ce{cell}=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \hspace{40px} \textrm{(Nernst equation)}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathit{0.0257\: V}}{n}\:\ln Q=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- ΔG = − célula NFe
- \(ΔG^∘=−nFE^\circ_\ce{cell}\)
- \(w_\ce{ele}=w_\ce{max}=−nFE_\ce{cell}\)
Glossário
- célula de concentração
- célula galvânica na qual as duas meias-células são iguais, exceto pela concentração dos solutos; espontânea quando a reação geral é a diluição do soluto
- trabalho elétrico (w ele)
- negativo da carga total vezes o potencial da célula; igual a w max para o sistema e, portanto, igual à mudança de energia livre (ΔG)
- Constante de Faraday (F)
- carga em 1 mol de elétrons; F = 96.485 C/mol e −
- Equação de Nernst
- equação que relaciona o logaritmo do quociente de reação (Q) com potenciais celulares não padrão; pode ser usada para relacionar constantes de equilíbrio com potenciais celulares padrão


