16.E: Termodinâmica (exercícios)

Last updated
Save as PDF

Page ID: 184632

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

16.1: Exercícios de espontaneidade

Q16.1.1

O que é uma reação espontânea?

S16.1.1

Uma reação tem uma tendência natural de ocorrer e ocorre sem a entrada contínua de energia de uma fonte externa.

Q16.1.2

O que é uma reação não espontânea?

Q16.1.3

Indique se os seguintes processos são espontâneos ou não espontâneos.

Congelamento de água líquida a uma temperatura abaixo do seu ponto de congelamento
Congelamento de água líquida a uma temperatura acima do seu ponto de congelamento
A combustão da gasolina
Uma bola jogada no ar
Uma gota de chuva caindo no chão
Ferrugem de ferro em uma atmosfera úmida

S16.1.2

espontâneo; não espontâneo; espontâneo; não espontâneo; espontâneo; espontâneo

Q16.1.4

Um balão cheio de hélio se esvazia espontaneamente durante a noite à medida que os átomos de He se difundem pela parede do balão. Descreva a redistribuição de matéria e/ou energia que acompanha esse processo.

Q16.1.5

Muitos materiais plásticos são polímeros orgânicos que contêm carbono e hidrogênio. A oxidação desses plásticos no ar para formar dióxido de carbono e água é um processo espontâneo; no entanto, os materiais plásticos tendem a persistir no meio ambiente. Explique.

S16.1.5

Embora a oxidação dos plásticos seja espontânea, a taxa de oxidação é muito lenta. Os plásticos são, portanto, cineticamente estáveis e não se decompõem consideravelmente, mesmo em períodos de tempo relativamente longos.

16.2: Exercícios de entropia

Q16.2.1

Na Figura abaixo, todas as distribuições e microestados possíveis são mostrados para quatro partículas diferentes compartilhadas entre duas caixas. Determine a mudança de entropia, ΔS, se as partículas forem inicialmente distribuídas uniformemente entre as duas caixas, mas após a redistribuição, todas acabarão na Caixa (b).

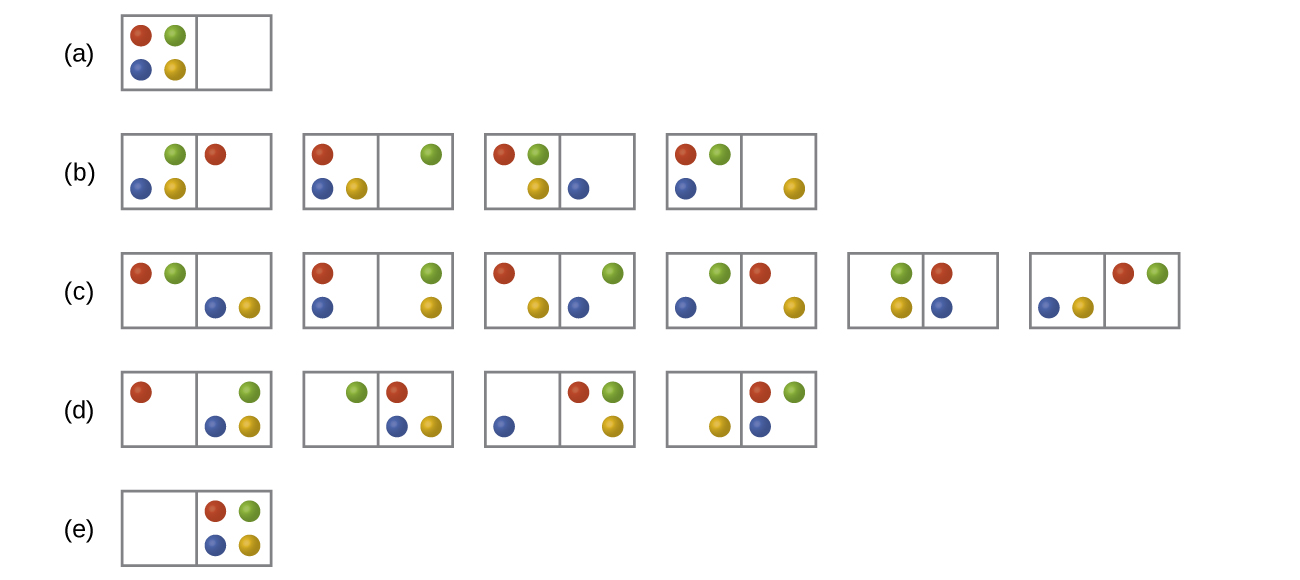
Q16.2.2

Na Figura, todas as distribuições e microestados possíveis são mostrados para quatro partículas diferentes compartilhadas entre duas caixas. Determine a mudança de entropia, ΔS, para o sistema quando ele é convertido de distribuição para distribuição (d).

S16.2.2

Existem quatro microestados iniciais e quatro microestados finais.

\[ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}=\mathrm{1.38×10^{−23}\:J/K×\ln\dfrac{4}{4}=0}\]

Q16.2.3

Como o processo descrito no item anterior se relaciona com o sistema mostrado em [link]?

Q16.2.4

Considere um sistema semelhante ao abaixo, exceto que ele contém seis partículas em vez de quatro. Qual é a probabilidade de ter todas as partículas em apenas uma das duas caixas da caixa? Compare isso com a probabilidade similar para o sistema de quatro partículas que derivamos ser igual\(\dfrac{1}{8}\) a. O que essa comparação nos diz sobre sistemas ainda maiores?

S16.2.4

A probabilidade de todas as partículas estarem de um lado é\(\dfrac{1}{32}\). Essa probabilidade é visivelmente menor do que o\(\dfrac{1}{8}\) resultado para o sistema de quatro partículas. A conclusão que podemos fazer é que a probabilidade de todas as partículas permanecerem em apenas uma parte do sistema diminuirá rapidamente à medida que o número de partículas aumentar e, por exemplo, a probabilidade de todas as moléculas de gás se acumularem em apenas um lado de uma sala à temperatura e pressão ambiente é insignificante, pois o número de moléculas de gás na sala é muito grande.

Q16.2.5

Considere o sistema mostrado na Figura. Qual é a mudança na entropia para o processo em que a energia é inicialmente associada apenas à partícula A, mas no estado final a energia é distribuída entre duas partículas diferentes?

Q16.2.6

Considere o sistema mostrado na Figura. Qual é a mudança na entropia para o processo em que a energia é inicialmente associada às partículas A e B, e a energia é distribuída entre duas partículas em caixas diferentes (uma em A-B, a outra em C-D)?

S16.2.6

Há apenas um estado inicial. Para o estado final, a energia pode estar contida nos pares A-C, A-D, B-C ou B-D. Portanto, há quatro estados finais possíveis.

\[ΔS=k\ln\left(\dfrac{W_\ce{f}}{W_\ce{i}}\right)=\mathrm{1.38×10^{−23}\:J/K×\ln\left(\dfrac{4}{1}\right)=1.91×10^{−23}\:J/K}\]

Q16.2.7

Organize os seguintes conjuntos de sistemas em ordem crescente de entropia. Suponha um mol de cada substância e a mesma temperatura para cada membro de um conjunto.

H ₂ (g), HBro ₄ (g), HBr (g)
H ₂ O (l), H ₂ O (g), H ₂ O (s)
He (g), Cl ₂ (g), P ₄ (g)

Q16.2.8

À temperatura ambiente, a entropia dos halogênios aumenta de I ₂ para Br ₂ para Cl ₂. Explique.

S16.2.8

As massas dessas moléculas sugeririam a tendência oposta em suas entropias. A tendência observada é resultado da variação mais significativa da entropia com um estado físico. À temperatura ambiente, I ₂ é um sólido, Br ₂ é um líquido e Cl ₂ é um gás.

Q16.2.9

Considere dois processos: sublimação de I ₂ (s) e fusão de I ₂ (s) (Nota: o último processo pode ocorrer na mesma temperatura, mas com uma pressão um pouco mais alta).

\[\ce{I2}(s)⟶\ce{I2}(g)\]

\[\ce{I2}(s)⟶\ce{I2}(l)\]

ΔS é positivo ou negativo nesses processos? Em qual dos processos a magnitude da mudança de entropia será maior?

Q16.2.11

Indique qual substância nos pares dados tem o maior valor de entropia. Explique suas escolhas.

C ₂ H ₅ OH (l) ou C ₃ H ₇ OH (l)
C ₂ H ₅ OH (l) ou C ₂ H ₅ OH (g)
2 horas (Hg)

S16.2.11

C ₃ H ₇ OH (l), pois é uma molécula maior (mais complexa e mais massiva) e, portanto, mais microestados descrevendo seus movimentos estão disponíveis a qualquer temperatura. C ₂ H ₅ OH (g) como está no estado gasoso. 2H (g), uma vez que a entropia é uma propriedade extensa e, portanto, dois átomos de H (ou dois moles de átomos de H) possuem o dobro da entropia de um átomo (ou um mol de átomos).

Q16.2.11

Preveja o sinal da mudança de entropia para os seguintes processos:

Um cubo de gelo é aquecido até perto de seu ponto de fusão.
A respiração exalada forma neblina em uma manhã fria.
A neve derrete.

Q16.2.12

Preveja o sinal da mudança de entalpia para os seguintes processos. Dê um motivo para sua previsão.

\(\ce{Pb^2+}(aq)+\ce{S^2-}(aq)⟶\ce{PbS}(s)\)
\(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)
\(\ce{2C6H14}(l)+\ce{19O2}(g)⟶\ce{14H2O}(g)+\ce{12CO2}(g)\)

S16.2.12

Negativo. A precipitação sólida relativamente ordenada diminui o número de íons móveis na solução. Negativo. Há uma perda líquida de três moles de gás de reagentes para produtos. Positivo. Há um aumento líquido de sete moles de gás de reagentes para produtos.

Q16.2.13

Escreva a equação química balanceada para a combustão do metano, CH ₄ (g), para dar dióxido de carbono e vapor de água. Explique por que é difícil prever se ΔS é positivo ou negativo para essa reação química.

Q16.2.14

Escreva a equação química balanceada para a combustão do benzeno, C ₆ H ₆ (l), para dar dióxido de carbono e vapor de água. Você esperaria que ΔS fosse positivo ou negativo nesse processo?

S16.2.14

\[\ce{C6H6}(l)+7.5\ce{O2}(g)⟶\ce{3H2O}(g)+\ce{6CO2}(g)\]

Existem 7,5 moles de gás inicialmente e 3 + 6 = 9 moles de gás no final. Portanto, é provável que a entropia aumente como resultado dessa reação, e ΔS seja positivo.

16.3: A Segunda e a Terceira Lei

Q16.3.0

Qual é a diferença entre ΔS, ΔS° e\(ΔS^\circ_{298}\) para uma mudança química?

Q16.3.1

Calcule\(ΔS^\circ_{298}\) para as seguintes alterações.

\(\ce{SnCl4}(l)⟶\ce{SnCl4}(g)\)
\(\ce{CS2}(g)⟶\ce{CS2}(l)\)
\(\ce{Cu}(s)⟶\ce{Cu}(g)\)
\(\ce{H2O}(l)⟶\ce{H2O}(g)\)
\(\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\)
\(\ce{2HCl}(g)+\ce{Pb}(s)⟶\ce{PbCl2}(s)+\ce{H2}(g)\)
\(\ce{Zn}(s)+\ce{CuSO4}(s)⟶\ce{Cu}(s)+\ce{ZnSO4}(s)\)

S16.3.1

107 J/K; −86,4 J/K; 133,2 J/K; 118,8 J/K; −326,6 J/K; −171,9 J/K; (g) −7,2 J/K

Q16.3.2

Determine a mudança de entropia para a combustão de etanol líquido, C ₂ H ₅ OH, sob condições de estado padrão para fornecer dióxido de carbono gasoso e água líquida.

Q16.3.3

Determine a mudança de entropia para a combustão do propano gasoso, C ₃ H ₈, sob condições de estado padrão para fornecer dióxido de carbono gasoso e água.

S16.3.3

10,6 KG/K

Q16.3.4

As reações de “termita” têm sido usadas para soldar peças de metal, como trilhos ferroviários e no refino de metais. Uma dessas reações de termita é:

\[\ce{Fe2O3}(s)+\ce{2Al}(s)⟶\ce{Al2O3}(s)+\ce{2Fe}(s)\]

A reação é espontânea à temperatura ambiente sob condições padrão? Durante a reação, o ambiente absorve 851,8 kJ/mol de calor.

Q16.3.5

Usando os\(S^\circ_{298}\) valores relevantes listados no Apêndice G, calcule\(S^\circ_{298}\) para as seguintes alterações:

\(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
\(\ce{N2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{N2O5}(g)\)

S 16.3.5

−198,1 M/K; −348,9 M/K

Q16.3.6

A partir das informações a seguir, determine\(ΔS^\circ_{298}\) o seguinte:

\(\ce{N}(g)+\ce{O}(g)⟶\ce{NO}(g) \hspace{20px} ΔS^\circ_{298}=\,?\)
\(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{24.8\: J/K}\)
\(\ce{N2}(g)⟶\ce{2N}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{115.0\: J/K}\)
\(\ce{O2}(g)⟶\ce{2O}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{117.0\: J/K}\)

Q16.3.7

Calculando ΔS _univ em cada temperatura, determine se a fusão de 1 mol de NaCl (s) é espontânea a 500 °C e a 700 °C.

\[S^\circ_{\ce{NaCl}(s)}=\mathrm{72.11\:\dfrac{J}{mol⋅K}}\hspace{40px} S^\circ_{\ce{NaCl}(l)}=\mathrm{95.06\:\dfrac{J}{mol⋅K}}\hspace{40px ΔH^\circ_\ce{fusion}=\mathrm{27.95\: kJ/mol}\]

Quais suposições são feitas sobre as informações termodinâmicas (valores de entropia e entalpia) usadas para resolver esse problema?

S16.3.7

Como ΔS _univ < 0 em cada uma dessas temperaturas, a fusão não é espontânea em nenhuma delas. Os valores dados para entropia e entalpia são para NaCl a 298 K. Supõe-se que eles não mudem significativamente nas temperaturas mais altas usadas no problema.

Q16.3.8

Use os dados de entropia padrão no Apêndice G para determinar a mudança na entropia para cada uma das reações listadas em [link]. Todos são executados em condições de estado padrão e 25 °C.

Q16.3.8

2,86 J/K; 24,8 J/K; −113,2 J/K; −24,7 J/K; 15,5 J/K; 290,0 J/K

16.4: Energia livre

Q16.4.1

Qual é a diferença entre ΔG, ΔG° e\(ΔG^\circ_{298}\) para uma mudança química?

Q16.4.2

A reação tem\(ΔH^\circ_{298}\) = 100 kJ/mol\(ΔS^\circ_{298}=\textrm{250 J/mol⋅K}\) e. A reação é espontânea à temperatura ambiente? Se não, sob quais condições de temperatura ele se tornará espontâneo?

S 16.4.2

A reação não é espontânea à temperatura ambiente. Acima de 400 K, ΔG se tornará negativo e a reação se tornará espontânea.

Q16.4.3

Explique o que acontece quando uma reação começa com ΔG < 0 (negativo) e atinge o ponto em que ΔG = 0.

Use os dados padrão de energia livre de formação no Apêndice G para determinar a mudança de energia livre para cada uma das seguintes reações, que são executadas em condições de estado padrão e 25 °C. Identifique cada uma como espontânea ou não espontânea nessas condições.

\(\ce{MnO2}(s)⟶\ce{Mn}(s)+\ce{O2}(g)\)
\(\ce{H2}(g)+\ce{Br2}(l)⟶\ce{2HBr}(g)\)
\(\ce{Cu}(s)+\ce{S}(g)⟶\ce{CuS}(s)\)
\(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g)\)
\(\ce{CH4}(g)+\ce{O2}(g)⟶\ce{C}(s,\,\ce{graphite})+\ce{2H2O}(g)\)
\(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g)\)

S16.4.3

465,1 kJ não espontâneo; −106,86 kJ espontâneo; −53,6 kJ espontâneo; −83,4 kJ espontâneo; −406,7 kJ espontâneo; −30,0 kJ espontâneo

Q16.4.4

Use os dados padrão de energia livre no Apêndice G para determinar a mudança de energia livre para cada uma das seguintes reações, que são executadas em condições de estado padrão e 25 °C. Identifique cada uma como espontânea ou não espontânea nessas condições.

\(\ce{C}(s,\, \ce{graphite})+\ce{O2}(g)⟶\ce{CO2}(g)\)
\(\ce{O2}(g)+\ce{N2}(g)⟶\ce{2NO}(g)\)
\(\ce{2Cu}(s)+\ce{S}(g)⟶\ce{Cu2S}(s)\)
\(\ce{CaO}(s)+\ce{H2O}(l)⟶\ce{Ca(OH)2}(s)\)
\(\ce{Fe2O3}(s)+\ce{3CO}(g)⟶\ce{2Fe}(s)+\ce{3CO2}(g)\)
\(\ce{CaSO4⋅2H2O}(s)⟶\ce{CaSO4}(s)+\ce{2H2O}(g)\)

Dado:

\[\ce{P4}(s)+\ce{5O2}(g)⟶\ce{P4O10}(s) \hspace{20px} ΔG^\circ_{298}=\mathrm{−2697.0\: kJ/mol}\]

\[\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{−457.18\: kJ/mol}\]

\[\ce{6H2O}(g)+\ce{P4O10}(g)⟶\ce{4H3PO4}(l) \hspace{20px} ΔG^\circ_{298}=\mathrm{−428.66\: kJ/mol}\]

Q16.4.5

Determine a energia livre padrão de formação,\(ΔG^\circ_\ce{f}\), para o ácido fosfórico.
Como seu resultado calculado se compara ao valor no Apêndice G? Explique.

S 16.4.5

−1124,3 kJ/mol para a mudança de energia livre padrão. O cálculo concorda com o valor no Apêndice G porque a energia livre é uma função de estado (assim como a entalpia e a entropia), então sua mudança depende apenas dos estados inicial e final, não do caminho entre eles.

Q16.4.6

A formação de ozônio (O ₃ (g)) a partir do oxigênio (O ₂ (g)) é espontânea à temperatura ambiente sob condições de estado padrão?

Q16.4.7

Considere a decomposição do óxido de mercúrio vermelho (II) sob condições de estado padrão.

\[\ce{2HgO}(s,\,\ce{red})⟶\ce{2Hg}(l)+\ce{O2}(g)\]

A decomposição é espontânea sob condições de estado padrão?
Acima de qual temperatura a reação se torna espontânea?

S16.4.7

A reação não é espontânea; Acima de 566° C, o processo é espontâneo.

Q16.4.8

Entre outras coisas, um combustível ideal para os propulsores de controle de um veículo espacial deve se decompor em uma reação exotérmica espontânea quando exposto ao catalisador apropriado. Avalie as seguintes substâncias em condições estaduais padrão como candidatas adequadas para combustíveis.

Amônia:\(\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g)\)
Diborano:\(\ce{B2H6}(g)⟶\ce{2B}(g)+\ce{3H2}(g)\)
Hidrazina:\(\ce{N2H4}(g)⟶\ce{N2}(g)+\ce{2H2}(g)\)
Peróxido de hidrogênio:\(\ce{H2O2}(l)⟶\ce{H2O}(g)+\dfrac{1}{2}\ce{O2}(g)\)

Q16.4.9

Calcule ΔG° para cada uma das seguintes reações a partir da constante de equilíbrio na temperatura dada.

\(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} \mathrm{T=2000\:°C} \hspace{20px} K_p=4.1×10^{−4}\)
\(\ce{H2}(g)+\ce{I2}(g)⟶\ce{2HI}(g) \hspace{20px} \mathrm{T=400\:°C} \hspace{20px} K_p=50.0\)
\(\ce{CO2}(g)+\ce{H2}(g)⟶\ce{CO}(g)+\ce{H2O}(g) \hspace{20px} \mathrm{T=980\:°C} \hspace{20px} K_p=1.67\)
\(\ce{CaCO3}(s)⟶\ce{CaO}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=900\:°C} \hspace{20px} K_p=1.04\)
\(\ce{HF}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{F-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=7.2×10^{−4}\)
\(\ce{AgBr}(s)⟶\ce{Ag+}(aq)+\ce{Br-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=3.3×10^{−13}\)

S16.4.9

1,5 × 10 ² kJ; −21,9 kJ; −5,34 kJ; −0,383 kJ; 18 kJ; 71 kJ

Q16.4.10

Calcule ΔG° para cada uma das seguintes reações a partir da constante de equilíbrio na temperatura dada.

\(\ce{Cl2}(g)+\ce{Br2}(g)⟶\ce{2BrCl}(g) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.7×10^{−2}\)
\(\ce{2SO2}(g)+\ce{O2}(g)⇌\ce{2SO3}(g) \hspace{20px} \mathrm{T=500\:°C} \hspace{20px} K_p=48.2\)
\(\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} \mathrm{T=60\:°C} \hspace{20px} K_p=\mathrm{0.196\: atm}\)
\(\ce{CoO}(s)+\ce{CO}(g)⇌\ce{Co}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=550\:°C} \hspace{20px} K_p=4.90×10^2\)
\(\ce{CH3NH2}(aq)+\ce{H2O}(l)⟶\ce{CH3NH3+}(aq)+\ce{OH-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.4×10^{−4}\)
\(\ce{PbI2}(s)⟶\ce{Pb^2+}(aq)+\ce{2I-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=8.7×10^{−9}\)

Q16.4.11

Calcule a constante de equilíbrio a 25 °C para cada uma das seguintes reações a partir do valor de ΔG° dado.

\(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2OF2}(g) \hspace{20px} ΔG°=\mathrm{−9.2\: kJ}\)
\(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} ΔG°=\mathrm{7.3\: kJ}\)
\(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} ΔG°=\mathrm{−79\: kJ}\)
\(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} ΔG°=\mathrm{−1.6\: kJ}\)
\(\ce{SnCl4}(l)⟶\ce{SnCl4}(l) \hspace{20px} ΔG°=\mathrm{8.0\: kJ}\)

S16.4.11

K = 41; K = 0,053; K = 6,9 × 10 ¹³; K = 1,9; K = 0,04

Q16.4.2

Calcule a constante de equilíbrio a 25 °C para cada uma das seguintes reações a partir do valor de ΔG° dado.

\(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} ΔG°=\mathrm{−10.88\: kJ}\)
\(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} ΔG°=\mathrm{3.4\: kJ}\)
\(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} ΔG°=\mathrm{−39\: kJ}\)
\(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} ΔG°=\mathrm{−141.82\: kJ}\)
\(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} ΔG°=\mathrm{−1.88\: kJ}\)

Q16.4.13

Calcule a constante de equilíbrio na temperatura dada.

(uma)\(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2F2O}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
\(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
\(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} \mathrm{(T=575\:°C)}\)
\(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} \mathrm{(T=−10.0\:°C)}\)
\(\ce{SnCl4}(l)⟶\ce{SnCl4}(g) \hspace{20px} \mathrm{(T=200\:°C)}\)

S16.4.13

Em cada um dos itens a seguir, o valor de ΔG não é dado à temperatura da reação. Portanto, devemos calcular ΔG° a partir dos valores ΔH° e ΔS° e, em seguida, calcular ΔG a partir da relação ΔG° = ΔH° − TΔS°.

K = 1,29
K = 2,51 × 10 ⁻³
K = 4,83 × 10 ³
K = 0,219
K = 16,1

Q16.4.14

Calcule a constante de equilíbrio na temperatura dada.

(uma)\(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
\(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
\(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} \mathrm{(T=125\:°C)}\)
\(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} \mathrm{(T=675\:°C)}\)
\(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} \mathrm{(T=90\:°C)}\)

Q16.4.15

Considere a seguinte reação a 298 K:

\[\ce{N2O4}(g)⇌\ce{2NO2}(g) \hspace{20px} K_P=0.142\]

Qual é a mudança de energia livre padrão nessa temperatura? Descreva o que acontece com o sistema inicial, em que os reagentes e produtos estão em estados padrão, à medida que ele se aproxima do equilíbrio.

S16.4.16

A mudança de energia gratuita padrão é\(ΔG^\circ_{298}=−RT\ln K=\mathrm{4.84\: kJ/mol}\). Quando reagentes e produtos estão em seus estados padrão (1 bar ou 1 atm), Q = 1. À medida que a reação avança em direção ao equilíbrio, a reação muda para a esquerda (a quantidade de produtos diminui enquanto a quantidade de reagentes aumenta): Q < 1 e\(ΔG_{298}\) se torna menos positiva à medida que se aproxima de zero. Em equilíbrio, Q = K e ΔG = 0.

Q16.4.17

Determine o ponto de ebulição normal (em kelvin) do dicloroetano, CH ₂ Cl ₂. Encontre o ponto de ebulição real usando a Internet ou alguma outra fonte e calcule o erro percentual na temperatura. Explique as diferenças, se houver, entre os dois valores.

Q16.4.18

Em que condições é\(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g)\) espontâneo?

S16.4.18

A reação será espontânea em temperaturas superiores a 287 K.

Q16.4.19

À temperatura ambiente, a constante de equilíbrio (K _w) para a autoionização da água é 1,00 × 10 ⁻¹⁴. Usando essas informações, calcule a mudança de energia livre padrão para a reação aquosa do íon hidrogênio com o íon hidróxido para produzir água. (Dica: A reação é o inverso da reação de autoionização.)

Q16.4.20

O sulfeto de hidrogênio é um poluente encontrado no gás natural. Após sua remoção, ele é convertido em enxofre pela reação\(\ce{2H2S}(g)+\ce{SO2}(g)⇌\dfrac{3}{8}\ce{S8}(s,\,\ce{rhombic})+\ce{2H2O}(l)\). Qual é a constante de equilíbrio para essa reação? A reação é endotérmica ou exotérmica?

S16.4.20

K = 5,35 × 10 ¹⁵

O processo é exotérmico.

Q16.4.21

Considere a decomposição de CaCO ₃ (s) em CaO (s) e CO ₂ (g). Qual é a pressão parcial de equilíbrio do CO ₂ à temperatura ambiente?

Q16.4.22

No laboratório, o cloreto de hidrogênio (HCl (g)) e a amônia (NH ₃ (g)) geralmente escapam de garrafas de suas soluções e reagem para formar o cloreto de amônio (NH ₄ Cl (s)), o esmalte branco frequentemente visto em vidrarias. Supondo que o número de moles de cada gás que escapa para a sala seja o mesmo, qual é a pressão parcial máxima de HCl e NH ₃ no laboratório em temperatura ambiente? (Dica: As pressões parciais serão iguais e estarão em seu valor máximo quando estiverem em equilíbrio.)

S16.4.22

1,0 × 10 ⁻⁸ atm. Esta é a pressão máxima dos gases nas condições indicadas.

Q16.4.23

O benzeno pode ser preparado a partir do acetileno. \(\ce{3C2H2}(g)⇌\ce{C6H6}(g)\). Determine a constante de equilíbrio a 25 °C e a 850 °C. A reação é espontânea em qualquer uma dessas temperaturas? Por que todo acetileno não é encontrado como benzeno?

Q16.4.24

O dióxido de carbono se decompõe em CO e O ₂ em temperaturas elevadas. Qual é a pressão parcial de equilíbrio do oxigênio em uma amostra a 1000 °C para a qual a pressão inicial de CO ₂ foi de 1,15 atm?

\[x=\mathrm{1.29×10^{−5}\:atm}=P_{\ce{O2}}\]

Q16.4.25

O tetracloreto de carbono, um importante solvente industrial, é preparado pela cloração do metano a 850 K.

\[\ce{CH4}(g)+\ce{4Cl2}(g)⟶\ce{CCl4}(g)+\ce{4HCl}(g)\]

Qual é a constante de equilíbrio para a reação a 850 K? O recipiente de reação precisaria ser aquecido ou resfriado para manter a temperatura da reação constante?

Q16.4.25 B

O ácido acético, CH ₃ CO ₂ H, pode formar um dímero, (CH ₃ CO ₂ H) ₂, na fase gasosa.

\[\ce{2CH3CO2H}(g)⟶\ce{(CH3CO2H)2}(g)\]

O dímero é mantido unido por duas ligações de hidrogênio com uma força total de 66,5 kJ por mol de dímero.

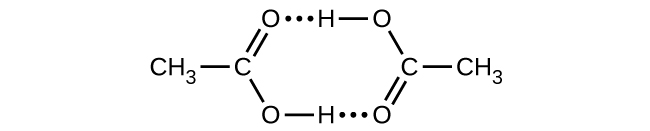
A 25 °C, a constante de equilíbrio para a dimerização é 1,3 × 10 ³ (pressão em atm). O que é ΔS° para a reação?

S16.4.25 B

−0,16 kJ

Q16.4.26

O ácido nítrico, HNO ₃, pode ser preparado pela seguinte sequência de reações:

\[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\]

\[\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\]

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(l)+\ce{NO}(g)\]

How much heat is evolved when 1 mol of NH₃(g) is converted to HNO₃(l)? Assume standard states at 25 °C.

Q16.4.27A

Determine ΔG for the following reactions.

(a) Antimony pentachloride decomposes at 448 °C. The reaction is:

\[\ce{SbCl5}(g)⟶\ce{SbCl3}(g)+\ce{Cl2}(g)\]

An equilibrium mixture in a 5.00 L flask at 448 °C contains 3.85 g of SbCl₅, 9.14 g of SbCl₃, and 2.84 g of Cl₂.

Chlorine molecules dissociate according to this reaction:

\[\ce{Cl2}(g)⟶\ce{2Cl}(g)\]

1.00% of Cl₂ molecules dissociate at 975 K and a pressure of 1.00 atm.

S16.4.27A

(a) −22.1 kJ;
61.6 kJ/mol

Q16.4.27

Given that the \(ΔG^\circ_\ce{f}\) for Pb²⁺(aq) and Cl⁻(aq) is −24.3 kJ/mole and −131.2 kJ/mole respectively, determine the solubility product, K_sp, for PbCl₂(s).

Q16.4.28

Determine the standard free energy change, \(ΔG^\circ_\ce{f}\), for the formation of S²⁻(aq) given that the \(ΔG^\circ_\ce{f}\) for Ag⁺(aq) and Ag₂S(s) are 77.1 k/mole and −39.5 kJ/mole respectively, and the solubility product for Ag₂S(s) is 8 × 10⁻⁵¹.

S16.4.28

90 kJ/mol

Q16.4.29

Determine the standard enthalpy change, entropy change, and free energy change for the conversion of diamond to graphite. Discuss the spontaneity of the conversion with respect to the enthalpy and entropy changes. Explain why diamond spontaneously changing into graphite is not observed.

Q16.4.30

The evaporation of one mole of water at 298 K has a standard free energy change of 8.58 kJ.

\[\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{8.58\: kJ}\]

(a) Is the evaporation of water under standard thermodynamic conditions spontaneous?
Determine the equilibrium constant, K_P, for this physical process.
By calculating ∆G, determine if the evaporation of water at 298 K is spontaneous when the partial pressure of water, \(P_{\ce{H2O}}\), is 0.011 atm.
If the evaporation of water were always nonspontaneous at room temperature, wet laundry would never dry when placed outside. In order for laundry to dry, what must be the value of \(P_{\ce{H2O}}\) in the air?

S16.4.30

(a) Under standard thermodynamic conditions, the evaporation is nonspontaneous; K_p = 0.031; The evaporation of water is spontaneous; \(P_{\ce{H2O}}\) must always be less than K_p or less than 0.031 atm. 0.031 atm represents air saturated with water vapor at 25 °C, or 100% humidity.

Q16.4.31

In glycolysis, the reaction of glucose (Glu) to form glucose-6-phosphate (G6P) requires ATP to be present as described by the following equation:

\[\mathrm{Glu + ATP ⟶ G6P + ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−17\: kJ}\]

In this process, ATP becomes ADP summarized by the following equation:

\[\mathrm{ATP⟶ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−30\: kJ}\]

Determine the standard free energy change for the following reaction, and explain why ATP is necessary to drive this process:

\[\mathrm{Glu⟶G6P} \hspace{20px} ΔG^\circ_{298}=\:?\]

Q16.4.32

One of the important reactions in the biochemical pathway glycolysis is the reaction of glucose-6-phosphate (G6P) to form fructose-6-phosphate (F6P):

\[\mathrm{G6P⇌F6P} \hspace{20px} ΔG^\circ_{298}=\mathrm{1.7\: kJ}\]

(a) Is the reaction spontaneous or nonspontaneous under standard thermodynamic conditions?
Standard thermodynamic conditions imply the concentrations of G6P and F6P to be 1 M, however, in a typical cell, they are not even close to these values. Calculate ΔG when the concentrations of G6P and F6P are 120 μM and 28 μM respectively, and discuss the spontaneity of the forward reaction under these conditions. Assume the temperature is 37 °C.

S16.4.32

(a) Nonspontaneous as \(ΔG^\circ_{298}>0\); \(ΔG^\circ_{298}=−RT\ln K,\) \(ΔG = 1.7×10^3 + \left(8.314 × 335 × \ln\dfrac{28}{128}\right) = \mathrm{−2.5\: kJ}\). The forward reaction to produce F6P is spontaneous under these conditions.

Q16.4.33

Without doing a numerical calculation, determine which of the following will reduce the free energy change for the reaction, that is, make it less positive or more negative, when the temperature is increased. Explain.

(a) \(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
\(\ce{HCl}(g)+\ce{NH3}(g)⟶\ce{NH4Cl}(s)\)
\(\ce{(NH4)2Cr2O7}(s)⟶\ce{Cr2O3}(s)+\ce{4H2O}(g)+\ce{N2}(g)\)
\(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)

When ammonium chloride is added to water and stirred, it dissolves spontaneously and the resulting solution feels cold. Without doing any calculations, deduce the signs of ΔG, ΔH, and ΔS for this process, and justify your choices.

S16.4.33

ΔG is negative as the process is spontaneous. ΔH is positive as with the solution becoming cold, the dissolving must be endothermic. ΔS must be positive as this drives the process, and it is expected for the dissolution of any soluble ionic compound.

Q16.4.34

An important source of copper is from the copper ore, chalcocite, a form of copper(I) sulfide. When heated, the Cu₂S decomposes to form copper and sulfur described by the following equation:

\[\ce{Cu2S}(s)⟶\ce{Cu}(s)+\ce{S}(s)\]

(a) Determine \(ΔG^\circ_{298}\) for the decomposition of Cu₂S(s).
The reaction of sulfur with oxygen yields sulfur dioxide as the only product. Write an equation that describes this reaction, and determine \(ΔG^\circ_{298}\) for the process.
The production of copper from chalcocite is performed by roasting the Cu₂S in air to produce the Cu. By combining the equations from Parts (a) and (b), write the equation that describes the roasting of the chalcocite, and explain why coupling these reactions together makes for a more efficient process for the production of the copper.

Q16.4.35

What happens to \(ΔG^\circ_{298}\) (becomes more negative or more positive) for the following chemical reactions when the partial pressure of oxygen is increased?

(a) \(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)
\(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{SO3}(g)\)
\(\ce{HgO}(s)⟶\ce{Hg}(l)+\ce{O2}(g)\)

S16.4.35

(a) Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
Increasing \(P_{\ce{O2}}\) will shift the equilibrium the reactants, which decreases the value of K. \(ΔG^\circ_{298}\) therefore becomes more positive.