16.4: Gibbs Energy
- Page ID
- 184646
- Defina a energia livre de Gibbs e descreva sua relação com a espontaneidade
- Calcule a mudança de energia livre padrão para um processo usando energias livres padrão de formação para seus reagentes e produtos
- Calcule a mudança de energia livre padrão para um processo usando entalpias de formação e as entropias de seus reagentes e produtos
- Explique como a temperatura afeta a espontaneidade de alguns processos
- Relacione as mudanças padrão de energia livre com as constantes de equilíbrio
Um dos desafios de usar a segunda lei da termodinâmica para determinar se uma reação química é espontânea é que devemos determinar a mudança de entropia para o sistema e a mudança de entropia para o ambiente. Um segundo desafio ao trabalhar com uma reação química é que precisamos levar em consideração a mistura das substâncias, um problema que não ocorre ao observar a mudança de fase se for uma substância pura. Uma abordagem alternativa envolvendo uma nova propriedade termodinâmica definida em termos de propriedades do sistema só foi introduzida no final do século XIX pelo matemático americano Josiah Willard Gibbs. Essa nova propriedade é chamada de energia livre de Gibbs (\(G\)) (ou simplesmente energia livre) e é definida em termos de entalpia e entropia de um sistema da seguinte forma:
\[G=H−TS \nonumber \]
A energia livre é uma função de estado e, em temperatura e pressão constantes, a mudança padrão de energia livre (ΔG°) pode ser expressa da seguinte forma:
\[ΔG^º_\ce{sys}=ΔH^º_\ce{sys}−TΔS^º_\ce{sys} \nonumber \]
(Por uma questão de simplicidade, o subscrito “sys” será omitido daqui em diante.) Podemos entender a relação entre essa propriedade do sistema e a espontaneidade de um processo lembrando a expressão da segunda lei derivada anteriormente:
\[ΔS_\ce{univ}=ΔS+\dfrac{q_\ce{surr}}{T} \nonumber \]
A primeira lei exige que\(q_{surr} = −q_{sys}\), e sob pressão constante\(q_{sys} = ΔH\), essa expressão possa ser reescrita da seguinte forma:
\[ΔS_\ce{univ}=ΔS−\dfrac{ΔH}{T} \nonumber \]
ΔH é a mudança de entalpia do sistema. Multiplicar os dois lados dessa equação por −T e reorganizar produz o seguinte:
\[−TΔS_\ce{univ}=ΔH−TΔS \nonumber \]
A comparação dessa equação com a anterior para troca de energia livre mostra a seguinte relação:
\[ΔG=−TΔS_\ce{univ} \label{6} \]
A mudança de energia livre é, portanto, um indicador confiável da espontaneidade de um processo, estando diretamente relacionada ao indicador de espontaneidade previamente identificado,\(ΔS_{univ}\). A tabela\(\PageIndex{1}\) resume a relação entre a espontaneidade de um processo e os sinais aritméticos desses indicadores.
| \(ΔS_{univ} > 0\) | ΔG < 0 | se move espontaneamente na direção para frente, como está escrito, para alcançar o equilíbrio |
| \(ΔS_{univ} < 0\) | ΔG > 0 |
não espontâneo na direção para frente, como está escrito, mas se move espontaneamente na direção inversa, como está escrito, para alcançar o equilíbrio |
| \(ΔS_{univ} = 0\) | ΔG = 0 | reversível (em equilíbrio) |
Calculando a mudança de energia livre
A energia livre é uma função de estado, portanto, seu valor depende apenas das condições dos estados inicial e final do sistema que sofreram alguma mudança. Uma abordagem conveniente e comum para o cálculo de mudanças de energia livre para mudanças físicas e reações químicas é o uso de compilações amplamente disponíveis de dados termodinâmicos de estado padrão. Um método envolve o uso de entalpias e entropias padrão para calcular as mudanças de energia livre padrão de acordo com a seguinte relação, conforme demonstrado no Exemplo\(\PageIndex{1}\).
\[ ΔG°=ΔH°−TΔS° \label{7} \]
É importante entender que, para mudanças de fase,\(\Delta G^º\) informa se a mudança de fase é espontânea ou não; acontecerá ou não acontecerá. Para reações químicas,\(\Delta G^º\) informa a extensão de uma reação. Em outras palavras,\(\Delta G^º\) pois uma reação indica quanto produto estará presente em equilíbrio. Uma reação com\(\Delta G^º\) < 0 é considerada favorecida pelo produto em equilíbrio; haverá mais produtos do que reagentes quando a reação atingir o equilíbrio. Uma reação com\(\Delta G^º\) > 0 é considerada favorecida pelo reagente em equilíbrio; haverá mais reagentes do que produtos quando a reação atingir o equilíbrio.
Use dados padrão de entalpia e entropia das Tabelas T1 ou T2 para calcular a mudança padrão de energia livre para a vaporização da água à temperatura ambiente (298 K). O que o valor computado de ΔG° diz sobre a espontaneidade dessa mudança física para uma substância pura?
Solução
O processo de interesse é o seguinte:
\[\ce{H2O}(l)⟶\ce{H2O}(g) \label{\(\PageIndex{8}\)} \]
A mudança padrão na energia livre pode ser calculada usando a seguinte equação:
\[ΔG^\circ_{298}=ΔH°−TΔS° \label{\(\PageIndex{9}\)} \]
Nas tabelas T1 ou T2, aqui estão os dados:
| Substância | \(ΔH^\circ_\ce{f}\ce{(kJ/mol)}\) | \(S^\circ_{298}\textrm{(J/K⋅mol)}\) |
|---|---|---|
| H 2 (L) | \ (ΔH^\ circ_\ ce {f}\ ce {(kJ/mol)}\)” style="text-align:center; ">−286,83 | \ (S^\ circ_ {298}\ textrm {(J/k⋅mol)}\)” style="text-align:center; ">70.0 |
| H 2 (Og) | \ (ΔH^\ circ_\ ce {f}\ ce {(kJ/mol)}\)” style="text-align:center; ">−241.82 | \ (S^\ circ_ {298}\ textrm {(J/k⋅mol)}\)” style="text-align:center; ">188.8 |
Combinando a 298 K:
\[\begin{align*} ΔH°&=ΔH^\circ_{298}=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \\[4pt] &=[−241.82\: kJ−(−285.83)]\:kJ/mol \\[4pt] &=44.01\: kJ/mol \\[4pt] ΔS° &=ΔS^\circ_{298}=S^\circ_{298}(\ce{H2O}(g))−S^\circ_{298}(\ce{H2O}(l)) \\[4pt] &=188.8\:J/mol⋅K−70.0\:J/K \\[4pt] &=118.8\:J/mol⋅K \end{align*} \nonumber \]
em seguida, use a Equação\ ref {7}:
\[ΔG°=ΔH°−TΔS° \nonumber \]
Convertendo tudo em kJ e combinando em 298 K:
\[\begin{align*}ΔG^\circ_{298} &=ΔH°−TΔS° \\[4pt] &=44.01\: kJ/mol−(298\: K×118.8\:J/mol⋅K)×\dfrac{1\: kJ}{1000\: J} \end{align*} \nonumber \]
\[\mathrm{44.01\: kJ/mol−35.4\: kJ/mol=8.6\: kJ/mol} \nonumber \]
A 298 K (25 °C) e\(ΔG^\circ_{298}>0\), portanto, a ebulição é não espontânea (não espontânea) a 298 K.
Use os dados padrão de entalpia e entropia das Tabelas T1 ou T2 para calcular a mudança de energia livre padrão para a reação mostrada aqui (298 K). O que o valor calculado para ΔG° diz sobre a extensão dessa reação em 298 K?
\[\ce{C2H6}(g)⟶\ce{H2}(g)+\ce{C2H4}(g) \nonumber \]
- Resposta
-
\(ΔG^\circ_{298}=\mathrm{102.0\: kJ/mol}\); a reação é favorecida pelo reagente em equilíbrio a 25 °C. Haverá\(\ce{C2H6}(g)\) mais do que\(\ce{H2}(g)\) e\(\ce{C2H4}(g) \) em equilíbrio
As mudanças de energia livre também podem usar a energia livre padrão de formação\( (ΔG^\circ_\ce{f})\), para cada um dos reagentes e produtos envolvidos na reação. A energia livre padrão de formação é a mudança de energia livre que acompanha a formação de um mol de uma substância a partir de seus elementos em seus estados padrão. Semelhante às entalpias padrão de formação,\( (ΔG^\circ_\ce{f})\) é, por definição, zero para substâncias elementares sob condições de estado padrão. A abordagem para calcular a mudança de energia livre para uma reação usando essa abordagem é a mesma demonstrada anteriormente para mudanças de entalpia e entropia. Para a reação
\[m\ce{A}+n\ce{B}⟶x\ce{C}+y\ce{D}, \nonumber \]
a variação padrão de energia livre à temperatura ambiente pode ser calculada como
\[ \begin{align} ΔG^\circ_{298}&=ΔG° \\[4pt] &=∑νΔG^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants})\\[4pt] &=[xΔG^\circ_\ce{f}(\ce{C})+yΔG^\circ_\ce{f}(\ce{D})]−[mΔG^\circ_\ce{f}(\ce{A})+nΔG^\circ_\ce{f}(\ce{B})]. \end{align} \nonumber \]
Considere a decomposição do óxido de mercúrio (II) amarelo.
\[\ce{HgO}(s,\,\ce{yellow})⟶\ce{Hg}(l)+ \ce{ 1/2 O2(g)} \nonumber \]
Calcule a variação de energia livre padrão à temperatura ambiente,\(ΔG^\circ_{298}\), usando:
- energias livres padrão de formação e
- entalpias padrão de formação e entropias padrão.
Os resultados indicam que a reação é favorecida pelo produto ou pelo reagente em equilíbrio?
Solução
Os dados necessários estão disponíveis nas Tabelas T1 ou T2 e são mostrados aqui.
| Composto | \(ΔG^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(ΔH^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(S^\circ_{298}\:\textrm{(J/K⋅mol)}\) |
|---|---|---|---|
| Go (s, amarelo) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">−58,43 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">−90,46 | \ (S^\ circ_ {298}\:\ textrm {(J/k⋅mol)}\)” style="text-align:center; ">71.13 |
| Hg (l) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (S^\ circ_ {298}\:\ textrm {(J/k⋅mol)}\)” style="text-align:center; ">75,9 |
| O (2 g) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (S^\ circ_ {298}\:\ textrm {(J/k⋅mol)}\)” style="text-align:center; ">205.2 |
(a) Usando energias livres de formação:
\[ \begin{align*} ΔG^\circ_{298}&=∑νGS^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔG^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔG^\circ_{298}\ce{O2}(g)\right]−1ΔG^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\:mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)\right]−1\: mol(−58.43\: kJ/mol)=58.43\: kJ/mol} \end{align*} \nonumber \]
(b) Usando entalpias e entropias de formação:
\[\begin{align*}ΔH^\circ_{298}&=∑νΔH^\circ_{298}(\ce{products})−∑νΔH^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔH^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔH^\circ_{298}\ce{O2}(g)\right]−1ΔH^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] &\mathrm{=[1\: mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)]−1\: mol(−90.46\: kJ/mol)=90.46\: kJ/mol} \\[4pt] ΔS^\circ_{298} &=∑νΔS^\circ_{298}(\ce{products})−∑νΔS^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔS^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔS^\circ_{298}\ce{O2}(g)\right]−1ΔS^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\: mol(75.9\: J/mol\: K)+\dfrac{1}{2}mol(205.2\: J/mol\: K)\right]−1\: mol(71.13\: J/mol\: K)=107.4\: J/mol\: K} \end{align*} \nonumber \]
então podemos usar a Equação\ ref7} diretamente:
\[\begin{align*}ΔG°&=ΔH°−TΔS°\\[4pt] &=\mathrm{90.46\: kJ−298.15\: K×107.4\: J/K⋅mol×\dfrac{1\: kJ}{1000\: J}} \\[4pt] &=\mathrm{(90.46−32.01)\:kJ/mol=58.45\: kJ/mol} \end{align*} \nonumber \]
Ambas as formas de calcular a mudança de energia livre padrão a 25° C fornecem o mesmo valor numérico (até três números significativos) e preveem que o processo é favorecido pelo reagente em equilíbrio à temperatura ambiente.
Calcule ΔG° usando (a) energias livres de formação e (b) entalpias de formação e entropias (Tabelas T1 ou T2). Os resultados indicam que a reação é favorecida pelo produto ou pelo reagente em equilíbrio a 25 °C?
\[\ce{C2H4}(g)⟶\ce{H2}(g)+\ce{C2H2}(g) \nonumber \]
- Resposta
-
141,5 kJ/mol, favorecido pelo reagente em equilíbrio
Dependência da temperatura da espontaneidade e extensão da reação
Como foi demonstrado anteriormente na seção deste capítulo sobre entropia, a espontaneidade de um processo pode depender da temperatura do sistema. As transições de fase, por exemplo, ocorrerão espontaneamente em uma direção ou outra, dependendo da temperatura da substância em questão. De forma semelhante, mas não idêntica, algumas reações químicas podem deixar de ser favorecidas pelo produto em equilíbrio para serem favorecidas pelo reagente em equilíbrio, dependendo da temperatura.
O valor numérico de\(\Delta G^º\) é sempre dependente da temperatura. Nesta seção, estamos determinando se o sinal de\(\Delta G^º\) depende ou não da temperatura.
Para ilustrar esse conceito, a equação que relaciona a mudança de energia livre com as mudanças de entalpia e entropia do processo é considerada:
\[ ΔG^º=ΔH^º−TΔS^º \nonumber \]
A extensão de um processo, conforme refletida no sinal aritmético de sua mudança padrão de energia livre, é então determinada pelos sinais das mudanças de entalpia e entropia e, em alguns casos, pela temperatura absoluta. Como T é a temperatura absoluta (Kelvin), ela só pode ter valores positivos. Portanto, existem quatro possibilidades em relação aos sinais das mudanças de entalpia e entropia:
- Tanto ΔH º quanto ΔS º são positivos. Essa condição descreve um processo endotérmico que envolve um aumento na entropia do sistema. Nesse caso, ΔG º será negativo se a magnitude do termo T ΔS º for maior que ΔH º. Se o termo T ΔS º for menor que ΔH º, a mudança de energia livre será positiva. Esse processo é favorecido pelo produto em equilíbrio em altas temperaturas e pelo reagente em equilíbrio em baixas temperaturas.
- Tanto ΔH º quanto ΔS º são negativos. Essa condição descreve um processo exotérmico que envolve uma diminuição na entropia do sistema. Nesse caso, ΔG º será negativo se a magnitude do termo T ΔS º for menor que ΔH º. Se a magnitude do termo T ΔS º for maior que ΔH º, a mudança de energia livre será positiva. Esse processo é favorecido pelo produto em equilíbrio em baixas temperaturas e pelo reagente em equilíbrio em altas temperaturas.
- ΔH º é positivo e ΔS º é negativo. Essa condição descreve um processo endotérmico que envolve uma diminuição na entropia do sistema. Nesse caso, ΔG º será positivo independentemente da temperatura. Esse processo é favorecido pelo reagente em equilíbrio em todas as temperaturas.
- ΔH º é negativo e ΔS º é positivo. Essa condição descreve um processo exotérmico que envolve um aumento na entropia do sistema. Nesse caso, ΔG º será negativo, independentemente da temperatura. Esse processo é preferido pelo produto em equilíbrio em todas as temperaturas.
Esses quatro cenários estão resumidos na Tabela\(\PageIndex{1}\)
|
Sinal de\(\Delta H^o\) |
Sinal de\(\Delta S^o\) |
Sinal de\(\Delta G^o\) |
Dependência de temperatura de\(\Delta G^o\) |
|---|---|---|---|
| \ (\ Delta H^o\) ">- | \ (\ Delta S^o\) ">+ | \ (\ Delta G^o\) ">- | \ (\ Delta G^o\) ">O sinal de\(\Delta G^o\) não depende da temperatura. A reação é favorecida pelo produto em equilíbrio em todas as temperaturas. |
| \ (\ Delta H^o\) ">+ | \ (\ Delta S^o\) ">- | \ (\ Delta G^o\) ">+ | \ (\ Delta G^o\) ">O sinal de\(\Delta G^o\) não depende da temperatura. A reação é favorecida pelo reagente em equilíbrio em todas as temperaturas. |
| \ (\ Delta H^o\) ">- | \ (\ Delta S^o\) ">- | \ (\ Delta G^o\) ">- ou + | \ (\ Delta G^o\) ">O sinal de\(\Delta G^o\) dose depende da temperatura. A reação será favorecida pelo produto em equilíbrio em temperaturas mais baixas. |
| \ (\ Delta H^o\) ">+ | \ (\ Delta S^o\) ">+ | \ (\ Delta G^o\) ">- ou + | \ (\ Delta G^o\) ">
O sinal de\(\Delta G^o\) não depende da temperatura. A reação será favorecida pelo produto em equilíbrio em temperaturas mais baixas. |
A combustão incompleta do carbono é descrita pela seguinte equação:
\[\ce{2C}(s)+\ce{O2}(g)⟶\ce{2CO}(g) \nonumber \]
O sinal\(\Delta G^º\) desse processo depende da temperatura?
Solução
Os processos de combustão são exotérmicos (\(ΔH^º < 0\)). Essa reação específica envolve um aumento na entropia devido ao aumento associado na quantidade de espécies gasosas (ganho líquido de um mol de gás\(ΔS^º > 0\)). A reação é, portanto, favorecida pelo produto em equilíbrio (\(ΔG^º < 0\)) em todas as temperaturas.
Aquecedores de mãos químicos populares geram calor pela oxidação do ferro pelo ar:
\[\ce{4Fe}(s)+\ce{3O2}(g)⟶\ce{2Fe2O3}(s) \nonumber \]
O sinal\(\Delta G^o\) desse processo depende da temperatura?
- Resposta
-
ΔH º e ΔS º são ambos negativos; a reação é favorecida pelo produto em equilíbrio em baixas temperaturas.
Ao considerar as conclusões tiradas sobre a dependência da temperatura do sinal de ΔG º, é importante ter em mente o que significam os termos “alto” e “baixo”. Como esses termos são adjetivos, as temperaturas em questão são consideradas altas ou baixas em relação a alguma temperatura de referência. Um processo que é favorecido pelo reagente em equilíbrio em uma temperatura, mas favorecido pelo produto em equilíbrio em outra temperatura, necessariamente sofrerá uma mudança na “extensão” (conforme refletido por seu ΔG º) à medida que a temperatura varia. Isso é claramente ilustrado por uma apresentação gráfica da equação de mudança de energia livre, na qual ΔG º é plotado no eixo y versus T no eixo x:
\[ΔG^º=ΔH^º−TΔS^º \nonumber \]
\[y=b+mx \nonumber \]
Esse gráfico é mostrado na Figura\(\PageIndex{2}\). Um processo cujas mudanças de entalpia e entropia são do mesmo sinal aritmético exibirá uma dependência de temperatura para o sinal de ΔG º, conforme representado pelas duas linhas amarelas no gráfico. Cada linha cruza de um domínio de espontaneidade (positivo ou negativo ΔG º) para o outro a uma temperatura característica do processo em questão. Essa temperatura é representada pelo intercepto x da linha, ou seja, o valor de T para o qual ΔG º é zero:
\[ΔG^º=0=ΔH^º−TΔS^º \nonumber \]
\[T=\dfrac{ΔH^º}{ΔS^º} \nonumber \]
Assim, dizer que um processo é favorecido pelo produto em equilíbrio em temperaturas “altas” ou “baixas” significa que a temperatura está acima ou abaixo, respectivamente, daquela temperatura na qual ΔG º para o processo é zero.
Nesta discussão, usamos duas descrições diferentes para o significado do sinal de ΔG º. Você deve estar ciente do significado de cada descrição.
a) Extensão da reação: Esta descrição é usada para prever a proporção das concentrações do produto e do reagente em equilíbrio. Nesta descrição, usamos o termo termodinâmico ΔG º para nos dizer a mesma informação que a constante < 0, K > de equilíbrio, K. Quando ΔG º 1, e a reação será favorecida pelo produto em equilíbrio. Quando ΔG º > 0, K< 1 e a reação é favorecida pelo reagente em equilíbrio. Quando ΔG º = 0, K = 1, e a reação terá quantidades aproximadamente iguais de produtos e reagentes em equilíbrio. Em todos os casos, a reação formará uma mistura de produtos e reagentes em equilíbrio. Usamos o sinal e a magnitude de ΔG º para nos dizer quanto produto será produzido se a reação atingir o equilíbrio.
b) Espontaneidade: Essa descrição é muito mais complicada porque envolve duas interpretações diferentes de como ocorre uma reação no estado padrão. Uma interpretação envolve o processo hipotético no qual a reação prossegue do ponto de partida dos reagentes puros até o ponto final dos produtos puros, com todas as substâncias isoladas em seus próprios recipientes sob condições de estado padrão. Na segunda interpretação, mais realista, a reação começa com todos os reagentes e todos os produtos em seu estado padrão em um recipiente. Em seguida, permitimos que essa mistura específica reaja em uma quantidade infinitesimalmente pequena para que possamos obter uma taxa de mudança na energia livre em relação à extensão da reação quando todos os reagentes e produtos são misturados e (essencialmente) em seus estados padrão. Embora cada interpretação descreva um cenário de reação diferente, o valor da diferença na energia livre e o valor da taxa de mudança na energia livre são o mesmo número. Se ΔG º < 0, dizemos que a reação é espontânea, o que significa que a reação prosseguiria na direção direta, conforme escrito, para formar produtos puros em seu estado padrão. Se ΔG º > 0, dizemos que a reação não é espontânea, o que significa que a reação prosseguiria na direção inversa, conforme escrito, para formar reagentes puros em seu estado padrão. Se ΔG º = 0, dizemos que nem os reagentes nem os produtos são favorecidos para serem formados.
Um tratamento detalhado do significado de ΔGº pode ser encontrado no artigo “Energia livre versus extensão da reação”, de Richard S. Treptow, Journal of Chemical Education, 1996, Volume 73 (1), 51-54.
Conforme definido no capítulo sobre líquidos e sólidos, o ponto de ebulição de um líquido é a temperatura na qual suas fases sólida e líquida estão em equilíbrio (ou seja, quando a vaporização e a condensação ocorrem em taxas iguais). Use as informações nas Tabelas T1 ou T2 para estimar o ponto de ebulição da água.
Solução
O processo de interesse é a seguinte mudança de fase:
Quando esse processo está em equilíbrio, ΔG = 0, então o seguinte é verdadeiro:
\[0=ΔH°−TΔS°\hspace{40px}\ce{or}\hspace{40px}T=\dfrac{ΔH°}{ΔS°} \nonumber \]
Usando os dados termodinâmicos padrão das Tabelas T1 ou T2,
\ [\ begin {align*}
ΔH°&=ΔH^\ circ_\ ce {f} (\ ce {H2O} (g)) −ΔH^\ circ_\ ce {f} (\ ce {H2O} (l))\ nonumber\\
&=\ mathrm {−241,82\: kJ/mol − (−285,83\: kJ/moL − (−285,83\: kJ/moL) l) =44,01\: kJ/mol}\ nonumber
\ end {align*}\ nonumber\]
\ [\ begin {align*}
ΔS°&=ΔS^\ circ_ {298} (\ ce {H2O} (g)) −ΔS^\ circ_ {298} (\ ce {H2O} (l))\ nonumber\\
&=\ mathrm {188.8\: J/k⋅mol−70.0\: J/k⋅mol=118,8\: J/k⋅mol}\ nonumber
\ end {align*}\ nonumber\]
\[T=\dfrac{ΔH°}{ΔS°}=\mathrm{\dfrac{44.01×10^3\:J/mol}{118.8\:J/K⋅mol}=370.5\:K=97.3\:°C} \nonumber \]
O valor aceito para o ponto de ebulição normal da água é 373,2 K (100,0° C) e, portanto, esse cálculo está de acordo razoável. Observe que os valores dos dados de alterações de entalpia e entropia usados foram derivados de dados padrão em 298 K (Tabelas T1 ou T2.). Se desejar, você pode obter resultados mais precisos usando mudanças de entalpia e entropia determinadas no ponto de ebulição real (ou pelo menos mais próximo) do ponto de ebulição real.
Use as informações nas Tabelas T1 ou T2 para estimar o ponto de ebulição do CS 2.
- Resposta
-
313 K (valor aceito 319 K).
Energia livre e equilíbrio
A mudança de energia livre de um processo pode ser vista como uma medida de sua força motriz. Um valor negativo para ΔG representa uma força motriz finita para o processo na direção para frente, enquanto um valor positivo representa uma força motriz para o processo na direção inversa. Quando ΔG é zero, as forças motrizes para frente e para trás são iguais e, portanto, o processo ocorre em ambas as direções na mesma taxa (o sistema está em equilíbrio).
No capítulo sobre equilíbrio, o quociente de reação, Q, foi introduzido como uma medida conveniente do status de um sistema de equilíbrio. Lembre-se de que Q é o valor numérico da expressão de ação em massa para o sistema e que você pode usar seu valor para identificar a direção na qual uma reação prosseguirá para alcançar o equilíbrio. Quando Q é menor que a constante de equilíbrio, K, a reação prosseguirá na direção direta até que o equilíbrio seja alcançado e Q = K. Por outro lado, se Q > K, o processo prosseguirá na direção inversa até que o equilíbrio seja alcançado.
A mudança de energia livre para um processo que ocorre com reagentes e produtos presentes em condições não padronizadas, ΔG, está relacionada à mudança de energia livre padrão, ΔG°, de acordo com esta equação:
\[ΔG=ΔG°+RT\ln Q \label{eq10A} \]
R é a constante do gás (8,314 J/K mol), T é o kelvin ou temperatura absoluta e Q é o quociente da reação. Podemos usar essa equação para prever a espontaneidade de um processo sob qualquer conjunto de condições, conforme ilustrado no Exemplo\(\PageIndex{1}\).
Qual é a mudança de energia livre para o processo mostrado aqui sob as condições especificadas?
T = 25 °C\(P_{\ce{N2}}=\mathrm{0.870\: atm}\),\(P_{\ce{H2}}=\mathrm{0.250\: atm}\), e\(P_{\ce{NH3}}=\mathrm{12.9\: atm}\)
\[\ce{2NH3}(g)⟶\ce{3H2}(g)+\ce{N2}(g) \hspace{20px} ΔG°=\mathrm{33.0\: kJ/mol} \nonumber \]
Solução SS
A equação\ ref {Eq10a} relaciona a mudança de energia livre à mudança de energia livre padrão e ao quociente de reação e pode ser usada diretamente:
\[\begin{align*} ΔG&=ΔG°+RT\ln Q \\[4pt] &=\mathrm{33.0\:\dfrac{kJ}{mol}+\left(8.314\:\dfrac{J}{mol\: K}×298\: K×\ln\dfrac{(0.250^3)×0.870}{12.9^2}\right)}\\[4pt] &=\mathrm{9680\:\dfrac{J}{mol}\:or\: 9.68\: kJ/mol} \end{align*} \nonumber \]
Como o valor computado para ΔG é positivo, a reação não é espontânea nessas condições. A reação prosseguirá na direção inversa para alcançar o equilíbrio.
Calcule a mudança de energia livre para essa mesma reação a 875 °C em uma mistura de 5,00 L contendo 0,100 mol de cada gás. A reação é espontânea nessas condições?
- Resposta
-
ΔG = −47 kJ; sim, a reação prossegue na direção direta, conforme escrito, para alcançar o equilíbrio.
Para um sistema em equilíbrio, Q = K e ΔG = 0, e a Equação\ ref {EQ10a} pode ser escrita como
\[ \underbrace{0=ΔG°+RT\ln K}_{\text{at equilibrium}} \nonumber \]
\[ΔG°=−RT\ln K \label{eq4A} \]
ou alternativamente
\[K=e^{−\frac{ΔG°}{RT}} \label{eq4B} \]
Essa forma da equação fornece uma ligação útil entre essas duas propriedades termodinâmicas essenciais e pode ser usada para derivar constantes de equilíbrio a partir de mudanças de energia livre padrão e vice-versa. As relações entre as mudanças padrão de energia livre e as constantes de equilíbrio estão resumidas na Tabela\(\PageIndex{1}\).
| K | ΔG° | Comentários |
|---|---|---|
| < 1 | > 0 | Os reagentes são mais abundantes em equilíbrio. |
| = 1 | = 0 | Reagentes e produtos são igualmente abundantes em equilíbrio. |
| > 1 | < 0 | Os produtos são mais abundantes em equilíbrio. |
Dado que as energias livres padrão de formação de Ag + (aq), Cl − (aq) e AgCl (s) são 77,1 kJ/mol, −131,2 kJ/mol e −109,8 kJ/mol, respectivamente, calcule o produto de solubilidade, K sp, para AgCl.
Solução
A reação de interesse é a seguinte:
\[\ce{AgCl}(s)⇌\ce{Ag+}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][Cl- ]} \nonumber \]
A mudança de energia livre padrão para essa reação é calculada primeiro usando energias livres de formação padrão para seus reagentes e produtos:
\[ \begin{align*} ΔG° =ΔG^\circ_{298} &=[ΔG^\circ_\ce{f}(\ce{Ag+}(aq))+ΔG^\circ_\ce{f}(\ce{Cl-}(aq))]−[ΔG^\circ_\ce{f}(\ce{AgCl}(s))] \\[4pt] &=[77.1\: kJ/mol−131.2\: kJ/mol]−[−109.8\: kJ/mol] \\[4pt] &=55.7\: kJ/mol \end{align*} \nonumber \]
A constante de equilíbrio para a reação pode então ser derivada de sua mudança de energia livre padrão via Equação\ ref {Eq4b}:
\[\begin{align*} K_\ce{sp}&=e^{−\dfrac{ΔG°}{RT}}=\exp\left(−\dfrac{ΔG°}{RT}\right) \\[4pt] &=\mathrm{\exp\left(−\dfrac{55.7×10^3\:J/mol}{8.314\:J/mol⋅K×298.15\:K}\right)}\\&=\mathrm{\exp(−22.470)=e^{−22.470}=1.74×10^{−10}} \end{align*} \nonumber \]
Use os dados termodinâmicos fornecidos nas Tabelas T1 ou T2 para calcular a constante de equilíbrio para a dissociação do tetróxido de dinitrogênio a 25 °C.
\[\ce{NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]
- Resposta
-
K = 6,9
Para ilustrar melhor a relação entre esses dois conceitos termodinâmicos essenciais, considere a observação de que as reações prosseguem espontaneamente em uma direção que, em última análise, estabelece o equilíbrio. Como pode ser mostrado ao traçar a mudança de energia livre versus a extensão da reação (por exemplo, conforme refletido no valor de Q), o equilíbrio é estabelecido quando a energia livre do sistema é minimizada (Figura\(\PageIndex{3}\)). Se um sistema estiver presente com reagentes e produtos presentes em quantidades não equilibradas (Q ≠ K), a reação prosseguirá espontaneamente na direção necessária para estabelecer o equilíbrio.
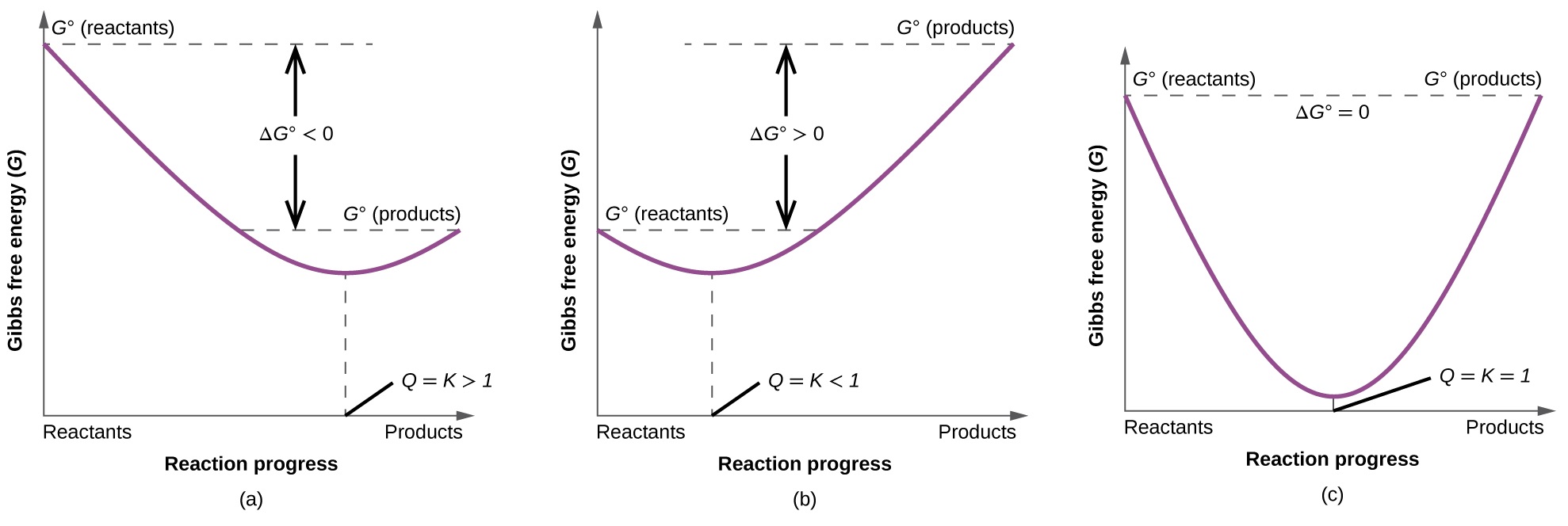
Resumo
A energia livre de Gibbs (G) é uma função de estado definida apenas em relação às quantidades do sistema e pode ser usada para prever a espontaneidade de um processo. Um valor negativo para ΔG indica que o processo prosseguirá na direção direta para alcançar o equilíbrio; um ΔG positivo indica que o processo prosseguirá na direção inversa para alcançar o equilíbrio; e um ΔG de zero indica que o sistema está em equilíbrio. Um valor negativo para ΔG º significa que a reação é favorecida pelo produto em equilíbrio. Um valor positivo para ΔG º significa que a reação é favorecida pelo reagente em equilíbrio. Se ΔG º for igual a 0 (uma ocorrência rara), a reação tem quantidades aproximadamente iguais de reagentes e produtos em equilíbrio. Várias abordagens para o cálculo de mudanças de energia livre são possíveis.
Equações chave
- ΔG = ΔH − T ΔS
- ΔG = ΔG° + RT em Q
- ΔG° = − RT em K
Glossário
- Mudança de energia livre de Gibbs (G)
- propriedade termodinâmica definida em termos de entalpia e entropia do sistema; todos os processos espontâneos envolvem uma diminuição em G
- mudança de energia livre padrão (ΔG°)
- mudança na energia livre para um processo que ocorre sob condições padrão (pressão de 1 bar para gases, concentração de 1 M para soluções)
- energia livre padrão de formação\( (ΔG^\circ_\ce{f})\)
- mudança na energia livre que acompanha a formação de um mol de substância a partir de seus elementos em seus estados padrão


