14.7: Titulações ácido-base

Last updated
Save as PDF

Page ID: 185540

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Interprete curvas de titulação para sistemas ácido-base fortes e fracos
Calcule o pH da amostra em estágios importantes de uma titulação
Explicar a função dos indicadores ácido-base

Conforme visto no capítulo sobre a estequiometria das reações químicas, as titulações podem ser usadas para analisar quantitativamente as soluções quanto às suas concentrações de ácido ou base. Nesta seção, exploraremos as mudanças nas concentrações das espécies ácidas e básicas presentes em uma solução durante o processo de titulação.

Curvas de titulação

Anteriormente, quando estudávamos as reações ácido-base em solução, nos concentrávamos apenas no ponto em que o ácido e a base eram estequiometricamente equivalentes. Nenhuma consideração foi dada ao pH da solução antes, durante ou após a neutralização.

Exemplo\(\PageIndex{1}\): Calculating pH for Titration Solutions: Strong Acid/Strong Base

Uma titulação é realizada para 25,00 mL de 0,100 M de HCl (ácido forte) com 0,100 M de uma base forte NaOH. A curva de titulação é mostrada na Figura\(\PageIndex{1}\). Calcule o pH nesses volumes da solução base adicionada:

0,00 mL
12,50 mL
25,00 mL
37,50 mL

Solução

Como o HCl é um ácido forte, podemos supor que tudo isso se dissocia. A concentração inicial de H ₃ O ⁺ é\(\ce{[H3O+]_0}=0.100\:M\). Quando a solução base é adicionada, ela também se dissocia completamente, fornecendo íons OH ⁻. Os íons H ₃ O ⁺ e OH ⁻ se neutralizam, então apenas os dois que estavam em excesso permanecem, e sua concentração determina o pH. Assim, a solução é inicialmente ácida (pH < 7), mas eventualmente todos os íons hidrônio presentes no ácido original são neutralizados e a solução se torna neutra. À medida que mais base é adicionada, a solução se torna básica.

A quantidade inicial total dos íons hidrônio é:

\[\mathrm{n(H^+)_0=[H_3O^+]_0×0.02500\: L=0.002500\: mol} \nonumber \]

Uma vez adicionado X mL da solução base de 0,100- M, o número de moles dos íons OH ⁻ introduzidos é:

\[\mathrm{n(OH^-)_0=0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

O volume total se torna:

\[V=\mathrm{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

O número de moles de H ₃ O ⁺ se torna:

\[\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0=0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

A concentração de H ₃ O ⁺ é:

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{V}=\dfrac{0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×X\: mL}{25.00\: mL+X\: mL}} \nonumber \]

com a definição de\(\mathrm{pH}\):

\[\mathrm{pH=−\log([H_3O^+])} \label{phdef} \]

Os cálculos anteriores funcionam se\(\mathrm{n(H^+)_0-n(OH^-)_0>0}\) e assim n (H ⁺) > 0. Quando\(\mathrm{n(H^+)_0=n(OH^-)_0}\), os íons H ₃ O ⁺ do ácido e os íons OH ⁻ da base se neutralizam mutuamente. Neste ponto, os únicos íons de hidrônio restantes são aqueles da autoionização da água, e não há partículas OH ⁻ para neutralizá-los. Portanto, neste caso:

\[\ce{[H3O+]}=\ce{[OH- ]},\:\ce{[H3O+]}=K_\ce{w}=1.0\times 10^{-14};\:\ce{[H3O+]}=1.0\times 10^{-7} \nonumber \]

\[\mathrm{pH=-log(1.0\times 10^{-7})=7.00} \nonumber \]

Finalmente\(\mathrm{n(OH^-)_0>n(H^+)_0}\), quando não há íons H ₃ O ⁺ suficientes para neutralizar todos os íons OH ⁻ e, em vez de\(\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0}\), calculamos:\(\mathrm{n(OH^-)=n(OH^-)_0-n(H^+)_0}\)

Nesse caso:

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)-0.002500\: mol}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.100\:\mathit{M}×X\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+X\: mL}} \nonumber \]

\(pH\)em seguida, usando a definição\(pOH\) e sua relação com soluções aquosas à temperatura ambiente (Equação\ ref {phdef}):

\[\begin{align} pH &=14-pOH \nonumber \\&=14+\log([OH^-]) \nonumber\end{align} \nonumber \]

Vamos agora considerar os quatro casos específicos apresentados neste problema:

(a) X = 0 mL

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL}=0.1\:\mathit{M}} \nonumber \]

em seguida, usando a definição de\(pH\) (Equação\ ref {phdef}):

\[\begin{align} pH &= −\log(0.100) \nonumber \\ &= 1.000 \nonumber\end{align} \nonumber \]

(b) X = 12,50 mL

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×12.50\: mL}{25.00\: mL+12.50\: mL}=0.0333\:\mathit{M}} \nonumber \]

em seguida, usando a definição de\(pH\) (Equação\ ref {phdef}):

\[ \begin{align} pH &= −\log(0.0333) \nonumber \\ &= 1.477 \nonumber\end{align} \nonumber \]

Como os volumes e concentrações das soluções ácidas e básicas são os mesmos:

\[\mathrm{n(H^+)_0=n(OH^-)_0} \nonumber \]

\[pH = 7.000 \nonumber \]

conforme descrito anteriormente.

(d) X = 37,50 mL

Nesse caso:

\[\mathrm{n(OH^-)_0>n(H^+)_0} \nonumber \]

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×35.70\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+37.50\: mL}=0.0200\:\mathit{M}} \nonumber \]

em seguida, usando a definição de\(pH\) (Equação\ ref {phdef}):

\[ \begin{align}[pH = 14 − pOH \nonumber\\ &= 14 + \log([OH^{−}]) \nonumber \\ &= 14 + \log(0.0200) \nonumber \\ &= 12.30 \nonumber \end{align} \nonumber \]

Exercício\(\PageIndex{1}\)

Calcule o pH para a titulação de ácido forte/base forte entre 50,0 mL de 0,100 M HNO ₃ (aq) e 0,200 M NaOH (titulante) nos volumes listados de base adicionada:

0,00 mL,
15,0 mL,
25,0 mL e
40,0 mL.

Responda a: 0,00:1.000
Resposta b: 15,0:1.5111
Resposta c: 25.0:7e. Não exclua esse texto primeiro.
Resposta d: 40,0:12.523

No exemplo\(\PageIndex{1}\), calculamos o pH em quatro pontos durante uma titulação. \(\PageIndex{1}\)A tabela mostra uma sequência detalhada de mudanças no pH de um ácido forte e um ácido fraco em uma titulação com NaOH.

Tabela\(\PageIndex{1}\): Valores de pH nas titulações de um ácido forte com uma base forte e de um ácido fraco com uma base forte
Volume de 0,100 M de NaOH adicionado (mL)	Toupeiras de NaOH adicionadas	Valores de pH 0,100 M HCl ¹	Valores de pH 0,100 M\(CH_3CO_2H\) ²
0,0	0,0	1,00	\ (CH_3CO_2H\) 2" style="alinhamento de texto: centro; ">2,87
5,0	0,00050	1,18	\ (CH_3CO_2H\) 2" style="text-align:center; ">4.14
10,0	0,00100	1,37	\ (CH_3CO_2H\) 2" style="alinhamento de texto: centro; ">4,57
15,0	0,00150	1,60	\ (CH_3CO_2H\) 2" style="alinhamento de texto: centro; ">4,92
20,0	0,00200	1,95	\ (CH_3CO_2H\) 2" style="text-align:center; ">5.35
22,0	0,00220	2,20	\ (CH_3CO_2H\) 2" style="text-align:center; ">5.61
24,0	0,00240	2,69	\ (CH_3CO_2H\) 2" style="text-align:center; ">6.13
24,5	0,00245	3,00	\ (CH_3CO_2H\) 2" style="text-align:center; ">6.44
24,9	0,00249	3,70	\ (CH_3CO_2H\) 2" style="text-align:center; ">7.14
25,0	0,00250	7,00	\ (CH_3CO_2H\) 2" style="text-align:center; ">8.72
25,1	0,00251	10,30	\ (CH_3CO_2H\) 2" style="text-align:center; ">10.30
25,5	0,00255	11,00	\ (CH_3CO_2H\) 2" style="text-align:center; ">11.00
26,0	0,00260	11,29	\ (CH_3CO_2H\) 2" style="text-align:center; ">11.29
28,0	0,00280	11,75	\ (CH_3CO_2H\) 2" style="alinhamento de texto: centro; ">11,75
30,0	0,00300	11,96	\ (CH_3CO_2H\) 2" style="text-align:center; ">11.96
35,0	0,00350	12,22	\ (CH_3CO_2H\) 2" style="text-align:center; ">12.22
40,0	0,00400	12,36	\ (CH_3CO_2H\) 2" style="text-align:center; ">12.36
45,0	0,00450	12,46	\ (CH_3CO_2H\) 2" style="text-align:center; ">12.46
50,0	0,00500	12,52	\ (CH_3CO_2H\) 2" style="text-align:center; ">12.52
\ (CH_3CO_2H\) 2" style="text-align:center; "> Titulação de 25,00 mL de 0,100 M HCl (0,00250 mol de HCI) com 0,100 M NaOH. Titulação de 25,00 mL de 0,100 M CH ₃ CO ₂ H (0,00250 mol de CH ₃ CO ₂ H) com 0,100 M NaOH.

As reações ácido-base mais simples são as de um ácido forte com uma base forte. A tabela\(\PageIndex{1}\) mostra dados para a titulação de uma amostra de 25,0 mL de ácido clorídrico 0,100 M com hidróxido de sódio 0,100 M. Os valores do pH medido após sucessivas adições de pequenas quantidades de NaOH estão listados na primeira coluna desta tabela e são representados graficamente na Figura\(\PageIndex{1}\), em uma forma que é chamada de curva de titulação. O pH aumenta lentamente no início, aumenta rapidamente na parte central da curva e depois aumenta lentamente novamente. O ponto de inflexão (localizado no ponto médio da parte vertical da curva) é o ponto de equivalência para a titulação. Indica quando quantidades equivalentes de ácido e base estão presentes. Para a titulação de um ácido forte com uma base forte, o ponto de equivalência ocorre em um pH de 7,00 e os pontos na curva de titulação podem ser calculados usando a estequiometria da solução (Tabela\(\PageIndex{1}\) e Figura\(\PageIndex{1}\)).

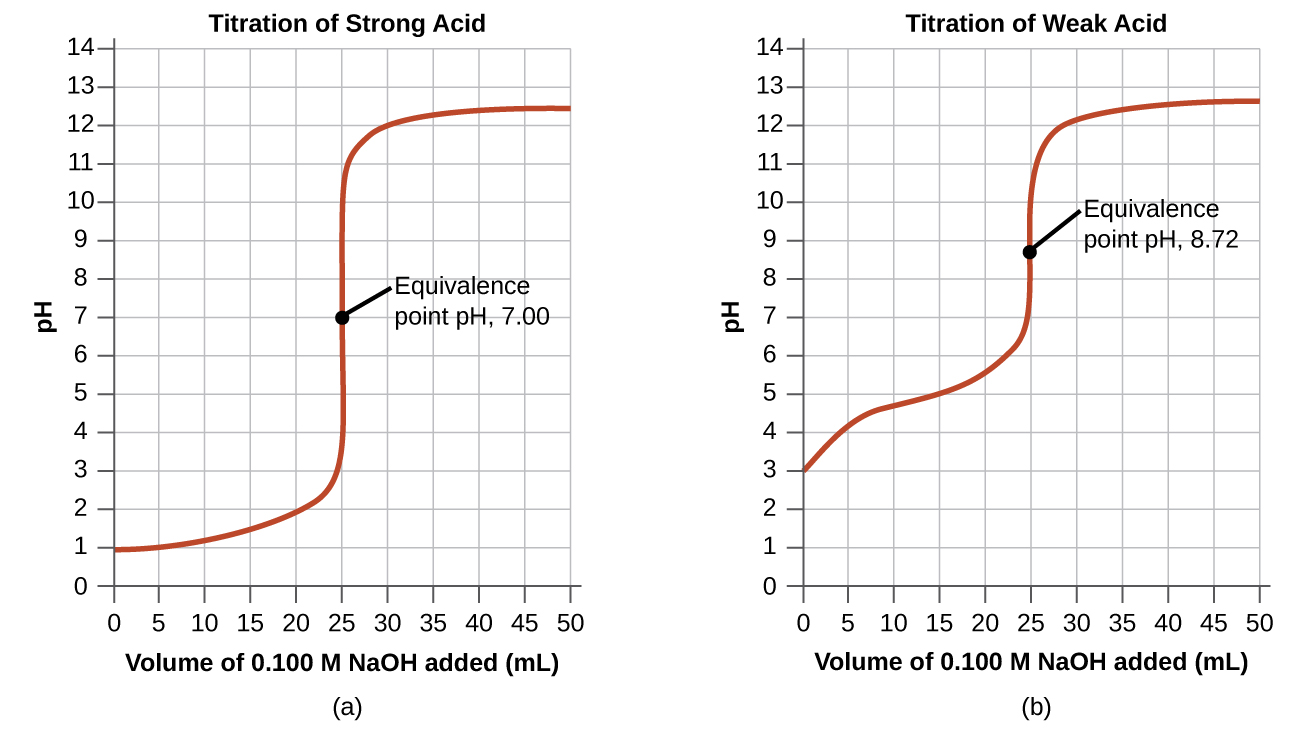
Figura\(\PageIndex{1}\): (a) A curva de titulação para a titulação de 25,00 mL de 0,100 M HCl (ácido forte) com 0,100 M NaOH (base forte) tem um ponto de equivalência de pH 7,00. (b) A curva de titulação para a titulação de 25,00 mL de 0,100 M CH ₃ CO ₂ H (ácido fraco) com 0,100 M NaOH (base forte) tem um ponto de equivalência de 8,72 pH.

A titulação de um ácido fraco com uma base forte (ou de uma base fraca com um ácido forte) é um pouco mais complicada do que a que acabamos de discutir, mas segue os mesmos princípios gerais. Vamos considerar a titulação de 25,0 mL de ácido acético 0,100 M (um ácido fraco) com 0,100 M de hidróxido de sódio e comparar a curva de titulação com a do ácido forte. A tabela\(\PageIndex{1}\) fornece os valores de pH durante a titulação, a Figura\(\PageIndex{1b}\) mostra a curva de titulação.

Embora o volume inicial e a molaridade dos ácidos sejam os mesmos, existem diferenças importantes entre as duas curvas de titulação. A curva de titulação do ácido fraco começa com um valor mais alto (menos ácido) e mantém valores de pH mais altos até o ponto de equivalência. Isso ocorre porque o ácido acético é um ácido fraco, que é apenas parcialmente ionizado. O pH no ponto de equivalência também é maior (8,72 em vez de 7,00) devido à hidrólise do acetato, uma base fraca que aumenta o pH:

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(l)+\ce{OH-}(aq) \nonumber \]

Após o ponto de equivalência, as duas curvas são idênticas porque o pH depende do excesso de íon hidróxido em ambos os casos.

Exemplo\(\PageIndex{2}\): Titration of a Weak Acid with a Strong Base

A curva de titulação mostrada na Figura\(\PageIndex{1b}\) é para a titulação de 25,00 mL de 0,100 M CH ₃ CO ₂ H com 0,100 M NaOH. A reação pode ser representada como:

\[\ce{CH3CO2H + OH- ⟶ CH3CO2- + H2O} \nonumber \]

Qual é o pH inicial antes de qualquer quantidade da solução de NaOH ser adicionada? K _a = 1,8 × 10 ⁻⁵ para CH ₃ CO ₂ H.
Encontre o pH após a adição de 25,00 mL da solução de NaOH.
Encontre o pH após a adição de 12,50 mL da solução de NaOH.
Encontre o pH após a adição de 37,50 mL da solução de NaOH.

Solução

(a) Supondo que a quantidade dissociada seja pequena em comparação com 0,100 M, descobrimos que:

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}≈\ce{\dfrac{[H3O+]^2}{[CH3CO2H]_0}} \nonumber \]

\[\ce{[H3O+]}=\sqrt{K_\ce{a}×\ce{[CH3CO2H]}}=\sqrt{1.8\times 10^{-5}×0.100}=1.3\times 10^{-3} \nonumber \]

\[\mathrm{pH=-\log(1.3\times 10^{-3})=2.87} \nonumber \]

(b) Após a adição de 25,00 mL de NaOH, o número de moles de NaOH e CH ₃ CO ₂ H é igual porque as quantidades das soluções e suas concentrações são as mesmas. Todo o CH ₃ CO ₂ H foi convertido em\(\ce{CH3CO2-}\). A concentração do\(\ce{CH3CO2-}\) íon é:

\[\mathrm{\dfrac{0.00250\: mol}{0.0500\: L}=0.0500\: \ce{MCH3CO2-}} \nonumber \]

O equilíbrio que deve ser focado agora é o equilíbrio básico para\(\ce{CH3CO2-}\):

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

então devemos determinar K _b para a base usando a constante do produto iônico para água:

\[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[CH3CO2- ][H+]}{[CH3CO2H]}},\textrm{ so }\ce{\dfrac{[CH3CO2H]}{[CH3CO2- ]}}=\dfrac{\ce{[H+]}}{K_\ce{a}}. \nonumber \]

Como K _w = [H ⁺] [OH ⁻]:

\[\begin{align} K_\ce{b} &=\dfrac{\ce{[H+][OH- ]}}{K_\ce{a}} \\ &=\dfrac{K_\ce{w}}{K_\ce{a}} \\ &=\dfrac{1.0\times 10^{-14}}{1.8\times 10^{-5}} \\ &=5.6\times 10^{-10} \end{align} \nonumber \]

Vamos denotar a concentração de cada um dos produtos dessa reação, CH ₃ CO ₂ H e OH ⁻, como x. Usando a suposição de que x é pequeno em comparação com 0,0500 M\(K_\ce{b}=\dfrac{x^2}{0.0500\:M}\), e então:

\[x=\ce{[OH- ]}=5.3\times 10^{−6} \nonumber \]

\[\ce{pOH}=-\log(5.3\times 10^{-6})=5.28 \nonumber \]

\[\ce{pH}=14.00−5.28=8.72 \nonumber \]

Observe que o pH no ponto de equivalência dessa titulação é significativamente maior que 7.

(c) Em (a), 25,00 mL da solução de NaOH foram adicionados e, portanto, praticamente todo o CH ₃ CO ₂ H foi convertido em\(\ce{CH3CO2-}\). Nesse caso, apenas 12,50 mL da solução base foram introduzidos e, portanto, apenas metade de todo o CH ₃ CO ₂ H é convertido em\(\ce{CH3CO2-}\). O número total inicial de moles de CH ₃ CO ₂ H é 0,02500L × 0,100 M = 0,00250 mol e, portanto, após a adição do NaOH, os números de moles de CH ₃ CO ₂ H e\(\ce{CH3CO2-}\) são ambos aproximadamente iguais a\(\mathrm{\dfrac{0.00250\: mol}{2}=0.00125\: mol}\), e seus as concentrações são as mesmas.

Como a quantidade da base adicionada é menor que a quantidade original do ácido, o ponto de equivalência não foi alcançado, a solução permanece um tampão e podemos usar a equação de Henderson-Hasselbalch:

\(\ce{pH}=\ce p K_\ce{a}+\log\ce{\dfrac{[Base]}{[Acid]}}=-\log(\mathit{K}_\ce{a})+\log\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]}}=-\log(1.8\times 10^{-5})+\log(1)\)

(já que as concentrações de\(\ce{CH3CO2-}\) e CH ₃ CO ₂ H são as mesmas)

Assim:

\[\ce{pH}=−\log(1.8\times 10^{−5})=4.74 \nonumber \]

_{(o pH = o p K a na metade da titulação de um ácido fraco)}

(d) Após a adição de 37,50 mL de NaOH, a quantidade de NaOH é 0,03750 L × 0,100 M = 0,003750 mol NaOH. Como isso ultrapassa o ponto de equivalência, o excesso de íons hidróxido tornará a solução básica, e podemos novamente usar cálculos estequiométricos para determinar o pH:

\(\mathrm{[OH^-]=\dfrac{(0.003750\: mol−0.00250\: mol)}{0.06250\: L}}=2.00\times 10^{−2}\:M\)

Então:

\(\mathrm{pOH=−\log(2.00\times 10^{−2})=1.70,\: and\: pH=14.00−1.70=12.30}\)

Observe que esse resultado é o mesmo do exemplo de titulação de base forte com ácido forte fornecido, uma vez que a quantidade de base forte adicionada move a solução além do ponto de equivalência.

Exercício\(\PageIndex{2}\)

Calcule o pH para a titulação de ácido fraco/base forte entre 50,0 mL de 0,100 M HCOOH (aq) (ácido fórmico) e 0,200 M NaOH (titulante) nos volumes listados de base adicionada:

0,00 mL,
15,0 mL,
25,0 mL e
30,0 mL.

Responda a: 0,00 mL: 2,37
Resposta b: 15,0 mL: 3,92
Resposta c: 25,00 mL: 8,29
Resposta d: 30,0 mL: 12,097

Indicadores ácido-base

Certas substâncias orgânicas mudam de cor na solução diluída quando a concentração do íon hidrônio atinge um valor específico. Por exemplo, a fenolftaleína é uma substância incolor em qualquer solução aquosa com uma concentração de íon hidrônio maior que 5,0 × 10 ⁻⁹ M (pH < 8,3). Em soluções mais básicas em que a concentração do íon hidrônio é menor que 5,0 × 10 ⁻⁹ M (pH > 8,3), ela é vermelha ou rosa. Substâncias como a fenolftaleína, que podem ser usadas para determinar o pH de uma solução, são chamadas de indicadores ácido-base. Os indicadores ácido-base são ácidos orgânicos fracos ou bases orgânicas fracas.

O equilíbrio em uma solução do indicador ácido-base laranja de metila, um ácido fraco, pode ser representado por uma equação na qual usamos\(\ce{HIn}\) como uma representação simples para a complexa molécula de laranja de metilo:

\[\underbrace{\ce{HIn (aq)}}_{\ce{red}}+\ce{H2O (l)}⇌\ce{H3O^{+} (aq)}+\underbrace{\ce{In^{-} (aq)}}_{\ce{yellow}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[H3O+][In- ]}{[HIn]}}=4.0\times 10^{−4} \nonumber \]

O ânion de metil laranja\(\ce{In^{-}}\),, é amarelo, e a forma não ionizada,\(\ce{HIn}\), é vermelha. Quando adicionamos ácido a uma solução de laranja de metilo, o aumento da concentração de íons hidrônio muda o equilíbrio para a forma vermelha não ionizada, de acordo com o princípio de Le Chatelier. Se adicionarmos base, mudamos o equilíbrio para a forma amarela. Esse comportamento é completamente análogo à ação dos buffers.

A cor de um indicador é o resultado visível da proporção das concentrações das duas espécies em ⁻\(\ce{HIn}\) e. Se a maior parte do indicador (normalmente cerca de 60 a 90% ou mais) estiver presente como\(\ce{In^{-}}\), então vemos a cor do\(\ce{In^{-}}\) íon, que seria amarelo para laranja de metilo. Se a maioria estiver presente como\(\ce{HIn}\), então vemos a cor da\(\ce{HIn}\) molécula: vermelho para laranja de metilo. Para laranja metílica, podemos reorganizar a equação para K _a e escrever:

\[\mathrm{\dfrac{[In^-]}{[HIn]}=\dfrac{[substance\: with\: yellow\: color]}{[substance\: with\: red\: color]}=\dfrac{\mathit{K}_a}{[H_3O^+]}} \label{ABeq2} \]

A equação\ ref {ABeQ2} nos mostra como a razão de\(\ce{\dfrac{[In- ]}{[HIn]}}\) varia com a concentração de íon hidrônio. A expressão acima que descreve o equilíbrio do indicador pode ser reorganizada:

\[ \begin{align} \dfrac{[H_3O^+]}{\mathit{K}_a} &=\dfrac{[HIn]}{[In^- ]} \\[8pt] \log\left(\dfrac{[H_3O^+]}{\mathit{K}_a}\right) &= \log\left(\dfrac{[HIn]}{[In^- ]}\right) \\[8pt] \log([H_3O^+])-\log(\mathit{K}_a) &=-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] -pH+p\mathit{K}_a & =-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] pH &=p\mathit{K}_a+\log\left(\dfrac{[In^-]}{[HIn]}\right) \end {align} \nonumber \]

ou em termos gerais

\[pH=p\mathit{K}_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{HHeq} \]

A equação\ ref {hHeq} é a mesma da equação de Henderson-Hasselbalch, que pode ser usada para descrever o equilíbrio dos indicadores.

_{Quando [H ₃ O ⁺] tem o mesmo valor numérico que K a, a razão de [In ⁻] para [HiN] é igual a 1, o que significa que 50% do indicador está presente na forma vermelha (HiN) e 50% está na forma iônica amarela (In ⁻), e a solução aparece} de cor laranja. Quando a concentração do íon hidrônio aumenta para 8 × 10 ⁻⁴ M (um pH de 3,1), a solução fica vermelha. Nenhuma mudança na cor é visível para qualquer aumento adicional na concentração de íons hidrônio (diminuição no pH). Em uma concentração de íon hidrônio de 4 × 10 ⁻⁵ M (um pH de 4,4), a maior parte do indicador está na forma iônica amarela e uma diminuição adicional na concentração de íons hidrônio (aumento no pH) não produz uma mudança de cor visível. A faixa de pH entre 3,1 (vermelho) e 4,4 (amarelo) é o intervalo de mudança de cor da laranja metil; a mudança de cor pronunciada ocorre entre esses valores de pH.

Há muitos indicadores ácido-base diferentes que abrangem uma ampla faixa de valores de pH e podem ser usados para determinar o pH aproximado de uma solução desconhecida por meio de um processo de eliminação. Os indicadores universais e o papel de pH contêm uma mistura de indicadores e exibem cores diferentes em diferentes pHs. \(\PageIndex{2}\)A figura apresenta vários indicadores, suas cores e seus intervalos de mudança de cor.

alt — Figura\(\PageIndex{2}\): Este gráfico ilustra as faixas de mudança de cor para vários indicadores ácido-base.

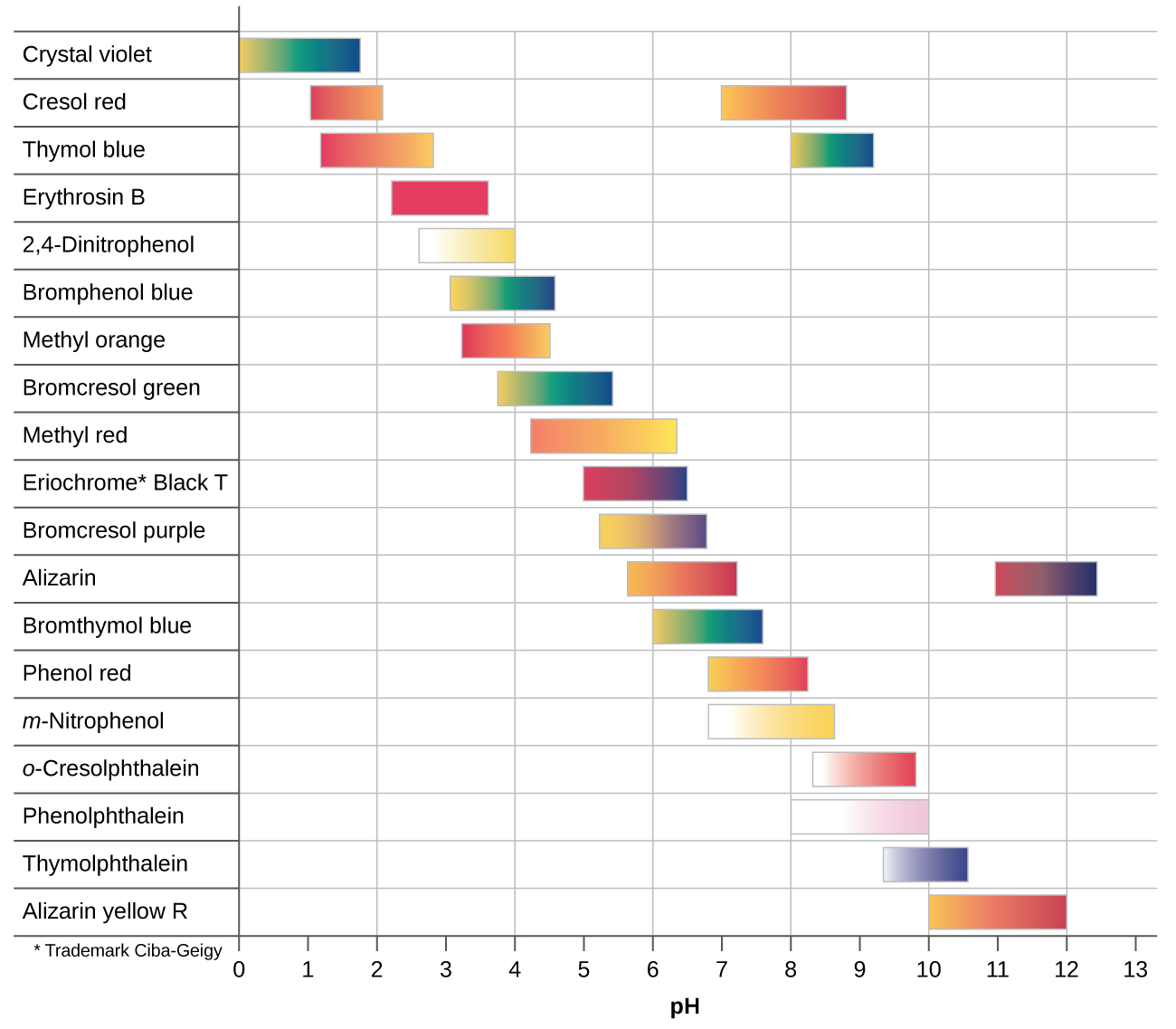
As curvas de titulação nos ajudam a escolher um indicador que fornecerá uma mudança de cor nítida no ponto de equivalência. A melhor seleção seria um indicador com um intervalo de mudança de cor entre parênteses o pH no ponto de equivalência da titulação.

Os intervalos de mudança de cor de três indicadores são mostrados na Figura\(\PageIndex{3}\). Os pontos de equivalência da titulação do ácido forte e do ácido fraco estão localizados no intervalo de mudança de cor da fenolftaleína. Podemos usá-lo para titulações de ácido forte com base forte ou ácido fraco com base forte.

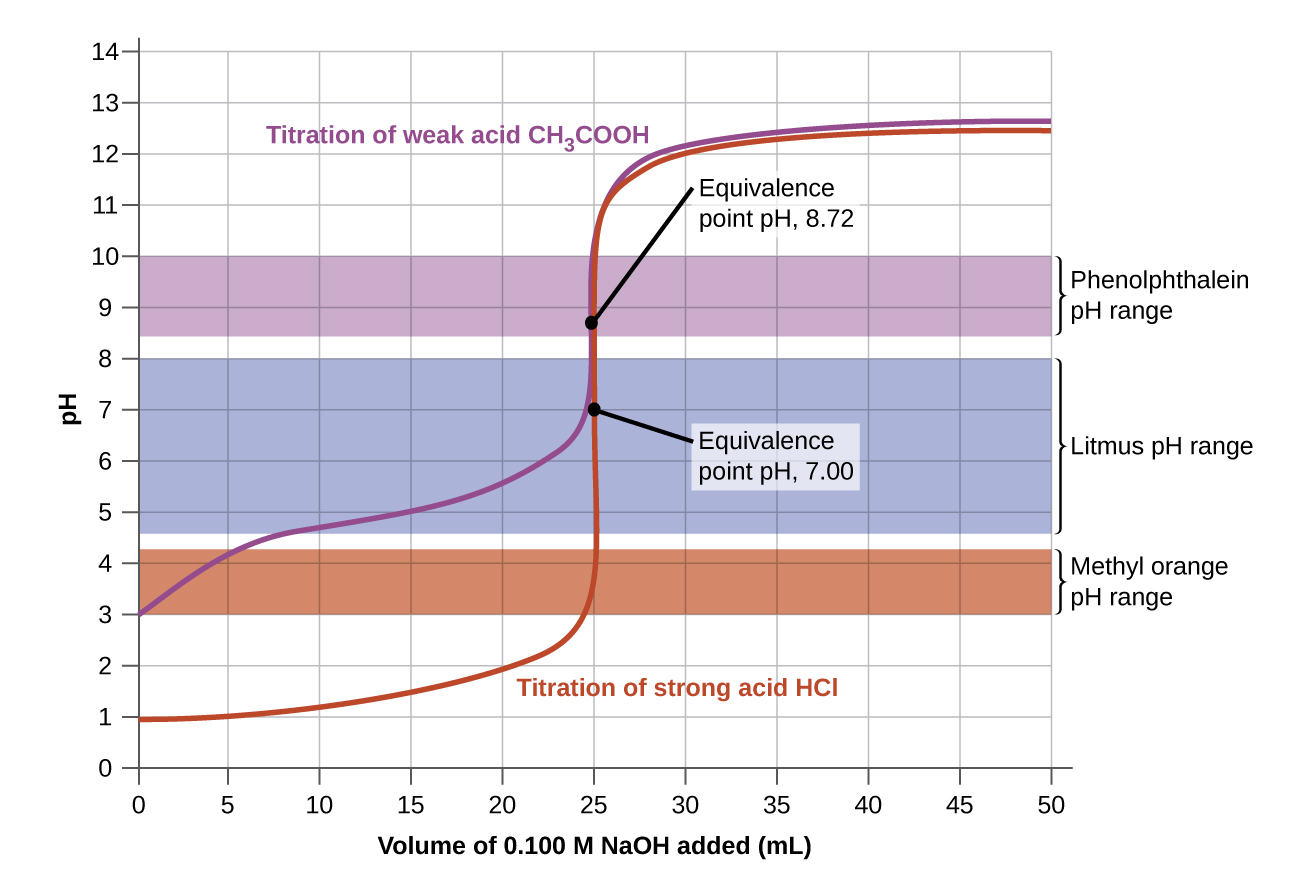
Figura\(\PageIndex{3}\): O gráfico mostra uma curva de titulação para a titulação de 25,00 mL de 0,100 M CH ₃ CO ₂ H (ácido fraco) com 0,100 M NaOH (base forte) e a curva de titulação para a titulação de HCl (ácido forte) com NaOH (base forte). As faixas de pH para a mudança de cor da fenolftaleína, tornassol e laranja metil são indicadas pelas áreas sombreadas.

Litmus é um indicador adequado para a titulação de HCl porque sua mudança de cor representa o ponto de equivalência. No entanto, não devemos usar tornassol para a titulação de CH ₃ CO ₂ H porque o pH está dentro do intervalo de mudança de cor do tornassol quando apenas cerca de 12 mL de NaOH foram adicionados e não sai da faixa até que 25 mL tenham sido adicionados. A mudança de cor seria muito gradual, ocorrendo durante a adição de 13 mL de NaOH, tornando o tornassol inútil como indicador do ponto de equivalência.

Poderíamos usar laranja de metilo para a titulação de HCl, mas isso não forneceria resultados muito precisos: (1) Ele completa sua mudança de cor um pouco antes que o ponto de equivalência seja atingido (mas muito próximo a ele, então isso não é muito sério); (2) ele muda de cor, como\(\PageIndex{2}\) demonstra a Figura, durante a adição de quase 0,5 mL de NaOH, que não é uma mudança de cor tão nítida quanto a de tornassol ou fenolftaleína; e (3) vai de amarelo para laranja e vermelho, tornando a detecção de um ponto final preciso muito mais desafiadora do que a mudança incolor para rosa da fenolftaleína. \(\PageIndex{2}\)A figura mostra que a laranja de metilo seria completamente inútil como indicador para a titulação de CH ₃ CO ₂ H. Sua mudança de cor começa após a adição de cerca de 1 mL de NaOH e termina quando cerca de 8 mL são adicionados. A mudança de cor é concluída muito antes de o ponto de equivalência (que ocorre quando 25,0 mL de NaOH foram adicionados) ser atingido e, portanto, não fornece nenhuma indicação do ponto de equivalência.

Baseamos nossa escolha de indicador em um pH calculado, o pH no ponto de equivalência. No ponto de equivalência, quantidades equimolares de ácido e base foram misturadas, e o cálculo passa a ser o do pH de uma solução do sal resultante da titulação.

Resumo

Uma curva de titulação é um gráfico que relaciona a mudança no pH de uma solução ácida ou básica com o volume de titulante adicionado. As características da curva de titulação dependem das soluções específicas que estão sendo tituladas. O pH da solução no ponto de equivalência pode ser maior que, igual ou menor que 7,00. A escolha de um indicador para uma determinada titulação depende do pH esperado no ponto de equivalência da titulação e da faixa de mudança de cor do indicador.

Glossário

indicador ácido-base: ácido orgânico ou base cuja cor muda dependendo do pH da solução em que se encontra

intervalo de mudança de cor: faixa de pH sobre a qual ocorre a mudança de cor de um indicador

curva de titulação: gráfico do pH de uma solução de ácido ou base versus o volume de base ou ácido adicionado durante uma titulação