14.5: Ácidos polipróticos
- Page ID
- 185581
- Estenda os conceitos de equilíbrio introduzidos anteriormente para ácidos e bases que podem doar ou aceitar mais de um próton
Podemos classificar os ácidos pelo número de prótons por molécula que eles podem liberar em uma reação. Ácidos como\(\ce{HCl}\)\(\ce{HNO3}\), e\(\ce{HCN}\) que contêm um átomo de hidrogênio ionizável em cada molécula são chamados de ácidos monopróticos. Suas reações com a água são:
\[\ce{HCl}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{Cl-}(aq) \nonumber \]
\[\ce{HNO3}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{NO3-}(aq) \nonumber \]
\[\ce{HCN}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{CN-}(aq) \nonumber \]
Embora contenha quatro átomos de hidrogênio, o ácido acético\(\ce{CH3CO2H}\),, também é monoprótico porque somente o átomo de hidrogênio do grupo carboxila (\(\ce{-COOH}\)) reage com as bases:

Da mesma forma, bases monopróticas são bases que aceitam um único próton.
Ácidos dipróticos
Os ácidos dipróticos contêm dois átomos de hidrogênio ionizáveis por molécula; a ionização desses ácidos ocorre em duas etapas. A primeira ionização sempre ocorre em maior medida do que a segunda ionização. Por exemplo, o ácido sulfúrico, um ácido forte, ioniza da seguinte forma:
- A primeira ionização é
\[ \ce{H2SO4}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HSO4-}(aq) \nonumber \]
com\(K_{\ce a1} > 10^2;\: {complete\: dissociation}\).
- A segunda ionização é
\[ \ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^{2−}}(aq) \nonumber \]
com\( K_{\ce a2}=1.2×10^{−2}\).
Esse processo de ionização gradual ocorre para todos os ácidos polipróticos. Quando fazemos uma solução de um ácido diprótico fraco, obtemos uma solução que contém uma mistura de ácidos. O ácido carbônico\(\ce{H2CO3}\),, é um exemplo de ácido diprótico fraco. A primeira ionização do ácido carbônico produz íons hidrônio e íons bicarbonato em pequenas quantidades.
- Primeira ionização
\[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \nonumber \]
com
\[K_{\ce{H2CO3}}=\ce{\dfrac{[H3O+][HCO3- ]}{[H2CO3]}}=4.3×10^{−7} \nonumber \]
O íon bicarbonato também pode atuar como ácido. Ele ioniza e forma íons hidrônio e íons carbonato em quantidades ainda menores.
- Segunda ionização
\[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \nonumber \]
com
\[ K_{\ce{HCO3-}}=\ce{\dfrac{[H3O+][CO3^2- ]}{[HCO3- ]}}=4.7×10^{−11} \nonumber \]
\(K_{\ce{H2CO3}}\)é maior do que\(K_{\ce{HCO3-}}\) por um fator de 10 4, então H 2 CO 3 é o produtor dominante de íon hidrônio na solução. Isso significa que pouco do\(\ce{HCO3-}\) formado pela ionização de H 2 CO 3 ioniza para dar íons hidrônio (e íons carbonato) e as concentrações de H 3 O + e\(\ce{HCO3-}\) são praticamente iguais em uma solução aquosa pura de H 2 CO 3.
Se a primeira constante de ionização de um ácido diprótico fraco for maior que a segunda por um fator de pelo menos 20, é apropriado tratar a primeira ionização separadamente e calcular as concentrações resultantes dela antes de calcular as concentrações das espécies resultantes da ionização subsequente. Isso pode simplificar consideravelmente nosso trabalho porque podemos determinar a concentração de H 3 O + e a base conjugada da primeira ionização e, em seguida, determinar a concentração da base conjugada da segunda ionização em uma solução com concentrações determinadas pela primeira ionização.
Quando compramos água com gás (água gaseificada), estamos comprando uma solução de dióxido de carbono na água. A solução é ácida porque o CO 2 reage com a água para formar ácido carbônico, H 2 CO 3. O que são\(\ce{[H3O+]}\)\(\ce{[HCO3- ]}\), e\(\ce{[CO3^2- ]}\) em uma solução saturada de CO 2 com uma inicial [H 2 CO 3] = 0,033 M?
\[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \hspace{20px} K_{\ce a1}=4.3×10^{−7} \label{step1} \tag{equilibrium step 1} \]
\[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \hspace{20px} K_{\ce a2}=4.7×10^{−11} \label{step2} \tag{equilibrium step 2} \]
Solução
Conforme indicado pelas constantes de ionização, H 2 CO 3 é um ácido muito mais forte do que\(\ce{HCO3-}\), assim\(\ce{H2CO3}\) como o produtor dominante de íon hidrônio em solução. Portanto, há duas partes na solução desse problema:
- Usando as quatro etapas habituais, determinamos a concentração de H 3 O + e\(\ce{HCO3-}\) produzida pela ionização de H 2 CO 3.
- Em seguida, determinamos a concentração de\(\ce{CO3^2-}\) em uma solução com a concentração de H 3 O + e\(\ce{HCO3-}\) determinada em (1).
Para resumir:
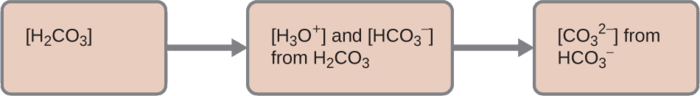
1. Primeira ionização: Determine as concentrações de\(\ce{H3O+}\) \(\ce{HCO3-}\)e.
Como\ ref {step1} é muito\(K_{a1}=4.3×10^{−7}\) maior do que\(K_{a2}=4.7×10^{−11}\)\ ref {step2}, podemos ignorar com segurança a segunda etapa de ionização e focar apenas na primeira etapa (mas resolvê-la na próxima parte do problema).
\[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \hspace{20px} K_{\ce a1}=4.3×10^{−7} \nonumber \]
Quanto à ionização de qualquer outro ácido fraco:

Uma tabela abreviada de mudanças e concentrações mostra:
| Tabela ICE | \(\ce{H2CO3}(aq)\) | \(\ce{H2O}(l)\) | \( \ce{H3O+}(aq) \) | \(\ce{HCO3-}(aq)\) |
|---|---|---|---|---|
| Inicialmente (M) | \ (\ ce {H2CO3} (aq)\)” style="text-align:center; ">\(0.033 \:M\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(0\) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\(0\) |
| Mudança C (MM) | \ (\ ce {H2CO3} (aq)\)” style="text-align:center; ">\(- x\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(+x\) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\(+x\) |
| Equilíbrio (M) | \ (\ ce {H2CO3} (aq)\)” style="text-align:center; ">\(0.033 \:M - x\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(x\) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\( x\) |
Substituir as concentrações de equilíbrio pela constante de equilíbrio nos dá:
\[K_{\ce{H2CO3}}=\ce{\dfrac{[H3O+][HCO3- ]}{[H2CO3]}}=\dfrac{(x)(x)}{0.033−x}=4.3×10^{−7} \nonumber \]
Resolver a equação anterior fazendo nossas suposições padrão fornece:
\[x=1.2×10^{−4} \nonumber \]
Assim:
\[\ce{[H2CO3]}=0.033\:M \nonumber \]
\[\ce{[H3O+]}=\ce{[HCO3- ]}=1.2×10^{−4}\:M \nonumber \]
2. Segunda ionização: Determine a concentração de \(CO_3^{2-}\)em uma solução em equilíbrio.
Como o\ ref {step1} é muito\(K_a\) maior que\ ref {step2}, podemos calcular as condições de equilíbrio da primeira parte do exemplo como as condições iniciais de uma tabela ICER para o\ ref {step2}:
\[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \nonumber \]
| Tabela ICE | \(\ce{HCO3-}(aq)\) | \(\ce{H2O}(l)\) | \( \ce{H3O+}(aq) \) | \(\ce{CO3^2-}(aq)\) |
|---|---|---|---|---|
| Inicialmente (M) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\(1.2×10^{−4}\:M\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(1.2×10^{−4}\:M\) | \ (\ ce {CO3^2-} (aq)\)” style="text-align:center; ">\(0\) |
| Mudança C (MM) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\(- y\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(+y\) | \ (\ ce {CO3^2-} (aq)\)” style="text-align:center; ">\(+y\) |
| Equilíbrio (M) | \ (\ ce {HCO3-} (aq)\)” style="text-align:center; ">\(1.2×10^{−4}\:M - y\) | \ (\ ce {H2O} (l)\)” style="text-align:center; ">- | \ (\ ce {H3O+} (aq)\)” style="text-align:center; ">\(1.2×10^{−4}\:M + y\) | \ (\ ce {CO3^2-} (aq)\)” style="text-align:center; ">\( y\) |
\[ \begin{align*} K_{\ce{HCO3-}}&=\ce{\dfrac{[H3O+][CO3^2- ]}{[HCO3- ]}} \\[4pt] &=\dfrac{(1.2×10^{−4}\:M + y) (y)}{(1.2×10^{−4}\:M - y)} \end{align*} \nonumber \]
Para evitar resolver uma equação quadrática, podemos supor\(y \ll 1.2×10^{−4}\:M \) que
\[K_{\ce{HCO3-}} = 4.7×10^{−11} \approx \dfrac{(1.2×10^{−4}\:M ) (y)}{(1.2×10^{−4}\:M)} \nonumber \]
Reorganizando para resolver\(y\)
\[y \approx \dfrac{ (4.7×10^{−11})(1.2×10^{−4}\:M )}{ 1.2×10^{−4}\:M} \nonumber \]
\[[\ce{CO3^2-}]=y \approx 4.7×10^{−11} \nonumber \]
Para resumir:
Na parte 1 deste exemplo, descobrimos que o\(\ce{H2CO3}\) em uma solução de 0,033- M ioniza levemente e em equilíbrio\([\ce{H2CO3}] = 0.033\, M\)\([\ce{H3O^{+}}] = 1.2 × 10^{−4}\),\(\ce{[HCO3- ]}=1.2×10^{−4}\:M\) e. Na parte 2, determinamos isso\(\ce{[CO3^2- ]}=5.6×10^{−11}\:M\).
A concentração de\(H_2S\) em uma solução aquosa saturada à temperatura ambiente é de aproximadamente 0,1 M. Calcule\(\ce{[H3O+]}\)\(\ce{[HS^{−}]}\), e\(\ce{[S^{2−}]}\) na solução:
\[\ce{H2S}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HS-}(aq) \hspace{20px} K_{\ce a1}=8.9×10^{−8} \nonumber \]
\[\ce{HS-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{S^2-}(aq) \hspace{20px} K_{\ce a2}=1.0×10^{−19} \nonumber \]
- Resposta
-
\([\ce{H2S}] = 0.1 M\),\(\ce{[H3O+]} = [HS^{−}] = 0.0001\, M\),\([S^{2−}] = 1 × 10^{−19}\, M\)
Observamos que a concentração do íon sulfeto é a mesma que K a2. Isso se deve ao fato de que cada dissociação subsequente ocorre em menor grau (à medida que o ácido fica mais fraco).
Ácidos tripróticos
Um ácido triprótico é um ácido que tem três prótons dissociáveis que sofrem ionização gradual: O ácido fosfórico é um exemplo típico:
- A primeira ionização é
\[\ce{H3PO4}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{H2PO4-}(aq) \nonumber \]
com\(K_{\ce a1}=7.5×10^{−3} \).
- A segunda ionização é
\[\ce{H2PO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HPO4^2-}(aq) \nonumber \]
com\( K_{\ce a2}=6.2×10^{−8} \).
- A terceira ionização é
\[\ce{HPO4^2-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{PO4^3-}(aq) \nonumber \]
com\( K_{\ce a3}=4.2×10^{−13} \).
Assim como acontece com os ácidos dipróticos, as diferenças nas constantes de ionização dessas reações nos dizem que em cada etapa sucessiva o grau de ionização é significativamente mais fraco. Essa é uma característica geral dos ácidos polipróticos e as sucessivas constantes de ionização geralmente diferem por um fator de cerca de 10 5 a 10 6. Esse conjunto de três reações de dissociação pode parecer complicar os cálculos das concentrações de equilíbrio em uma solução de H 3 PO 4. No entanto, como as constantes de ionização sucessivas diferem por um fator de 10 5 a 10 6, os cálculos podem ser divididos em uma série de partes semelhantes às dos ácidos dipróticos.
As bases polipróticas podem aceitar mais de um íon hidrogênio em solução. O íon carbonato é um exemplo de base diprótica, pois pode aceitar até dois prótons. As soluções de carbonatos de metais alcalinos são bastante alcalinas, devido às reações:
\[\ce{H2O}(l)+\ce{CO3^2-}(aq)⇌\ce{HCO3-}(aq)+\ce{OH-}(aq) \nonumber \]
e
\[\ce{H2O}(l)+\ce{HCO3-}(aq)⇌\ce{H2CO3}(aq)+\ce{OH-}(aq) \nonumber \]
Resumo
Um ácido que contém mais de um próton ionizável é um ácido poliprótico. Os prótons desses ácidos ionizam em etapas. As diferenças nas constantes de ionização ácida para as sucessivas ionizações dos prótons em um ácido poliprótico geralmente variam em aproximadamente cinco ordens de magnitude. Desde que a diferença entre os valores sucessivos de K a do ácido seja maior do que cerca de um fator de 20, é apropriado dividir os cálculos das concentrações dos íons em solução em uma série de etapas.
Glossário
- ácido diprótico
- ácido contendo dois átomos de hidrogênio ionizáveis por molécula. Um ácido diprótico ioniza em duas etapas
- base diprótica
- base capaz de aceitar dois prótons. Os prótons são aceitos em duas etapas
- ácido monoprótico
- ácido contendo um átomo de hidrogênio ionizável por molécula
- ionização gradual
- processo no qual um ácido é ionizado pela perda sequencial de prótons
- ácido triprótico
- ácido que contém três átomos de hidrogênio ionizáveis por molécula; a ionização dos ácidos tripróticos ocorre em três etapas


