12.E: Cinética (exercícios)
- Page ID
- 185026
12.1: Taxas de reação química
Q12.1.1
Qual é a diferença entre taxa média, taxa inicial e taxa instantânea?
- Solução
-
Primeiro, uma taxa de reação geral deve ser definida para saber o que é qualquer variação de uma taxa. A taxa de reação é definida como a medida da mudança na concentração dos reagentes ou produtos por unidade de tempo. A taxa de uma reação química não é constante e, ao contrário, muda continuamente e pode ser influenciada pela temperatura. A taxa de uma reação pode ser definida como o desaparecimento de qualquer reagente ou a aparência de qualquer produto. Assim, uma taxa média é a taxa média de reação durante um determinado período de tempo na reação, a taxa instantânea é a taxa de reação em um determinado momento durante a reação e a taxa inicial é a taxa instantânea no início da reação (quando o produto começa a se formar).
A taxa instantânea de uma reação pode ser indicada como\[ \lim_{\Delta t \rightarrow 0} \dfrac{\Delta [concentration]}{\Delta t} \nonumber \]
Q12.1.2
O ozônio se decompõe em oxigênio de acordo com a equação\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Escreva a equação que relaciona as expressões de taxa para essa reação em termos do desaparecimento de O 3 e da formação de oxigênio.
- Solução
-
Para a reação geral, aA —> bB, a taxa da reação pode ser expressa em termos do desaparecimento de A ou do aparecimento de B durante um determinado período de tempo, da seguinte forma.
\[- \dfrac{1}{a}\dfrac{\Delta [A]}{\Delta t} = - \dfrac{1}{b}\dfrac{\Delta [B]}{\Delta t} = \dfrac{1}{c}\dfrac{\Delta [C]}{\Delta t} = \dfrac{1}{d}\dfrac{\Delta [D]}{\Delta t}\]
Queremos que a taxa de uma reação seja positiva, mas a mudança na concentração de um reagente, A, será negativa porque está sendo usada para ser transformada em produto, B. Portanto, ao expressar a taxa da reação em termos da mudança na concentração de A, é importante adicionar um sinal negativo na frente para garantir que a taxa geral seja positiva.
Por fim, a taxa deve ser normalizada de acordo com a estequiometria da reação. Na decomposição do ozônio em oxigênio, dois moles de ozônio formam três moles de gás oxigênio. Isso significa que o aumento do gás oxigênio será 1,5 vezes maior que a diminuição do ozônio. Como a taxa da reação deve ser capaz de descrever ambas as espécies, dividimos a mudança na concentração por seu coeficiente estequiométrico na equação de reação balanceada para lidar com esse problema.
Portanto, a taxa da reação da decomposição do ozônio em gás oxigênio pode ser descrita da seguinte forma:
\[Rate=-\frac{Δ[O3]}{2ΔT}=\frac{Δ[O2]}{3ΔT}\]
- Resposta
-
$Taxa=-\ frac {Δ[ O3]} {2ΔT} =\ frac {δ [O2]} {3ΔT}\]
Q12.1.3
Na indústria nuclear, o trifluoreto de cloro é usado para preparar o hexafluoreto de urânio, um composto volátil de urânio usado na separação de isótopos de urânio. O trifluoreto de cloro é preparado pela reação\(\ce{Cl2}(g)+\ce{3F2}(g)⟶\ce{2ClF3}(g)\). Escreva a equação que relaciona as expressões de taxa para essa reação em termos do desaparecimento de Cl 2 e F 2 e da formação de ClF 3.
- Solução
-
Neste problema, somos convidados a escrever a equação que relaciona expressões de taxa em termos de desaparecimento dos reagentes da equação e em termos da formação do produto. Uma taxa de reação fornece uma visão de como a taxa é afetada em função da concentração das substâncias na equação. As taxas geralmente podem ser expressas em gráficos de concentração versus tempo expresso em mudança (\({\Delta}\)) de concentração e tempo e em um intervalo de tempo curto o suficiente, a taxa instantânea pode ser aproximada. Se analisássemos a reação dada, o gráfico demonstraria que Cl 2 diminui, que F 2 diminui 3 vezes mais rapidamente e, em seguida, ClF 3 aumenta a uma taxa dobra. Os reagentes estão sendo usados e convertidos em produto para que diminuam à medida que os produtos aumentam.
Para este problema, podemos aplicar a fórmula geral de uma taxa aos aspectos específicos de um problema em que a forma geral segue:\[aA+bB⟶cC+dD\nonumber \].
E a taxa pode então ser escrita como\(rate=-\frac {1}{a}\frac{{\Delta}[A]}{{\Delta}t}\)\(=-\frac {1}{b}\frac{{\Delta}[B]}{{\Delta}t}\)\(=\frac {1}{c}\frac{{\Delta}[C]}{{\Delta}t}\)\(=\frac {1}{d}\frac{{\Delta}[D]}{{\Delta}t}.\) Aqui, os sinais negativos são usados para manter a convenção de expressar taxas como números positivos.
Nesse caso específico, usamos a estequiometria para obter as taxas específicas de desaparecimento e formação (voltando ao que foi dito no primeiro parágrafo). Então, o problema envolve apenas referir-se à equação e seus coeficientes balanceados. Com base na equação, vemos que Cl 2 é um reagente e não tem coeficiente, F 2 tem um coeficiente de 3 e também é usado, e então ClF 3 é um produto que aumenta duas vezes com um coeficiente de 2. Então, a taxa aqui pode ser escrita como:\[rate=-\frac{{\Delta}[Cl_2]}{{\Delta}t}=-\frac {1}{3}\frac{{\Delta}[F_2]}{{\Delta}t}=\frac {1}{2}\frac{{\Delta}[ClF_3]}{{\Delta}t}\nonumber \]
- Resposta
-
\[\ce{rate}=+\dfrac{1}{2}\dfrac{Δ[\ce{CIF3}]}{Δt}=−\dfrac{Δ[\ce{Cl2}]}{Δt}=−\dfrac{1}{3}\dfrac{Δ[\ce{F2}]}{Δt}\nonumber \]
Q12.1.4
Um estudo da taxa de dimerização de C 4 H 6 forneceu os dados mostrados na tabela:
\[\ce{2C4H6⟶C8H12}\nonumber \]
| Hora (s) | 0 | 1600 | 3200 | 4800 | 6200 |
|---|---|---|---|---|---|
| [C 4 H 6] (M) | 1,00 × 10 −2 | 5,04 × 10 −3 | 3,37 × 10 −3 | 2,53 × 10 −3 | 2,08 × 10 −3 |
- Determine a taxa média de dimerização entre 0 s e 1600 s e entre 1600 s e 3200 s.
- Estime a taxa instantânea de dimerização em 3200 s a partir de um gráfico de tempo versus [C 4 H 6]. Quais são as unidades dessa taxa?
- Determine a taxa média de formação de C 8 H 12 a 1600 s e a taxa instantânea de formação a 3200 s a partir das taxas encontradas nas partes (a) e (b).
- Solução
-
1.) A taxa média de dimerização é a mudança na concentração de um reagente por unidade de tempo. Nesse caso, seria:
\(rate\)\(of\)\(dimerization=-\frac{\Delta [C_4H_6]}{\Delta t}\)
Taxa de dimerização entre 0 s e 1600 s:
\(rate\)\(of\)\(dimerization=-\frac{5.04×10^{-3}M-1.00×10^{-2}M}{1600 s-0 s}\)
\(rate\)\(of\)\(dimerization=3.10 × 10^{-6} \frac{M}{s}\)
Taxa de dimerização entre 1600 s e 3200 s:
\(rate\)\(of\)\(dimerization=-\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(rate\)\(of\)\(dimerization=1.04 × 10^{-6} \frac{M}{s}\)
2.) A taxa instantânea de dimerização a 3200 s pode ser encontrada representando graficamente o tempo versus [C 4 H 6].
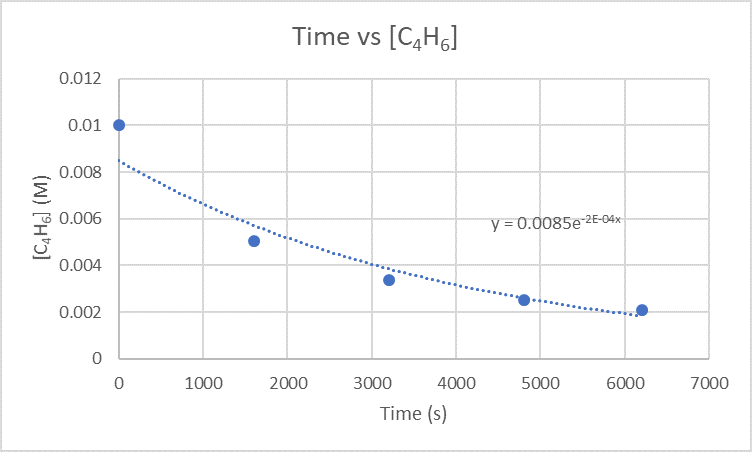
Como você deseja encontrar a taxa de dimerização em 3200 s, você precisa encontrar a inclinação entre 1600 s e 3200 s e também 3200 s e 4800 s.
Para a inclinação entre 1600 s e 3200 s, use os pontos (1600 s, 5,04 x 10 -3 M) e (3200 s, 3,37 x 10 -3 M)
\(\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(\frac{-0.00167 M}{1600 s}\)
\(-1.04×10^{-6}\frac{M}{s}\)
Para a inclinação entre 3200 s e 4800 s, use os pontos (3200s, 3,37 x 10 -3 M) e (4800s, 2,53 x 10 -3 M)
\(\frac{2.53×10^{-3}M-3.37×10^{-3}M}{4800 s-3200 s}\)
\(\frac{-8.4×10^{-4} M}{1600 s}\)
\(-5.25×10^{-7}\frac{M}{s}\)
Pegue as duas inclinações que você acabou de encontrar e encontre a média delas para obter a taxa instantânea de dimerização.
\(\frac{-1.04×10^{-6}\frac{M}{s}+-5.25×x10^{-7}\frac{M}{s}}{2}\)
\(\frac{-1.565×10^{-6}\frac{M}{s}}{2}\)
\(-7.83×10^-7\frac{M}{s}\)
A taxa instantânea de dimerização é \(-7.83×10^-7\frac{M}{s}\)e as unidades dessa taxa são \(\frac{M}{s}\).
3.) A taxa média de formação de C 8 H 12 a 1600 s e a taxa instantânea de formação a 3200 s podem ser encontradas usando nossas respostas das partes a e b. Se você olhar para a equação original, poderá ver que C 4 H 6 e C 8 H 12 estão relacionados em uma proporção de dois para um. Para cada dois moles de C 4 H 6 usados, há um mol de C 8 H 12 produzido.
Para essa reação, a taxa média de dimerização e a taxa média de formação podem ser vinculadas por meio desta equação:
\(\frac{-1}{2}\frac{\Delta [C_4H_6]}{\Delta t}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
Observe que o lado do reagente é negativo porque os reagentes estão sendo usados na reação.
Portanto, para a taxa média de formação de C 8 H 12 a 1600 s, use a taxa de dimerização entre 0 s e 1600 s que encontramos anteriormente e conecte à equação:
\(\frac{-1}{2}×3.10 × 10^{-6} \frac{M}{s}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
\(\frac{\Delta [C_8H_{12}]}{\Delta t}=1.55×10^{-6}\frac{M}{s}\)
A taxa média de formação para C 8 H 12 a 1600 s é\(1.55×10^{-6}\frac{M}{s}\). A taxa de formação será positiva porque os produtos estão sendo formados.
A taxa instantânea de formação para C 8 H 12 pode ser ligada à taxa instantânea de dimerização por esta equação:
\(\frac{-1}{2}\frac{d[C_4H_6]}{dt}=\frac{d[C_8H_{12}]}{dt}\)
Portanto, para a taxa instantânea de formação para C 8 H 12 a 3200 s, use o valor da taxa instantânea de dimerização em 3200 s encontrada anteriormente e conecte à equação:
\(\frac{-1}{2}×-7.83×10^-7\frac{M}{s}=\frac{d[C_8H_{12}]}{dt}\)
\(\frac{d[C_8H_{12}]}{dt}=-3.92×10^{-7}\frac{M}{s}\)
A taxa instantânea de formação para C 8 H 12 a 3200 s é\(-3.92×10^-7\frac{M}{s}\)
- Resposta
-
- \(3.10 × 10^{-6} \frac{M}{s}\)e\(1.04 × 10^{-6} \frac{M}{s}\)
- \(-7.83×10^-7\frac{M}{s}\)e\(\frac{M}{s}\)
- \(-3.92×10^-7\frac{M}{s}\)
Q12.1.5
Um estudo da taxa da reação representada\(2A⟶B\) forneceu os seguintes dados:
| Hora (s) | 0,0 | 5,0 | 10,0 | 15,0 | 20,0 | 25,0 | 35,0 |
|---|---|---|---|---|---|---|---|
| [A] (M) | 1,00 | 0,952 | 0,625 | 0,465 | 0,370 | 0,308 | 0,230 |
- Determine a taxa média de desaparecimento de A entre 0,0 s e 10,0 s e entre 10,0 s e 20,0 s.
- Estime a taxa instantânea de desaparecimento de A em 15,0 s a partir de um gráfico de tempo versus [A]. Quais são as unidades dessa taxa?
- Use as taxas encontradas nas partes (a) e (b) para determinar a taxa média de formação de B entre 0,00 s e 10,0 s, e a taxa instantânea de formação de B em 15,0 s.
- Solução
-
Equações:\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) e Rate=\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\)
Resolver: 1.) A mudança em A de 0s para 10s é .625-1=-.375 então\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) =.375/10= 0.0374 M/s
Da mesma forma, a mudança em A de 10 para 20 segundos é .370-.625 = -.255, então\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) =.255/20-10= 0,0255M/s
2.) Podemos estimar a lei de taxas representando graficamente os pontos em relação a equações de ordem diferente para determinar a ordem correta.
Ordem zero:\[\frac{d[A]}{dt}=-k\nonumber \]\[\int_{A_{\circ}}^{A}d[A]=-k\int_{0}^{t}dt\nonumber \]\[[A]=-kt+[A_{\circ}]\nonumber \]
Primeiro pedido:\[\frac{d[A]}{dt}=-k[A]\nonumber \]\[\int_{A_{\circ}}^{A}\frac{d[A]}{[A]}=-kdt\nonumber \]\[Ln(A)=-kt+Ln(A_{\circ})\nonumber \]
Segunda ordem:\[\frac{d[A]}{dt}=-k[A]^{2}\nonumber \]\[\int_{A\circ}^{A}\frac{d[A]}{[A]^{2}}=-k\int_{0}^{t}dt\nonumber \]
\[\frac{1}{[A]}=kt+\frac{1}{[A_{\circ}]}\nonumber \]
Agora que encontramos a forma linear de cada ordem, traçaremos os pontos versus um eixo y [A], um eixo y Ln (A) e um eixo y 1/ [A]. Qualquer um dos gráficos com os pontos mais lineares nos dará uma boa ideia da ordem e a inclinação será o valor k.
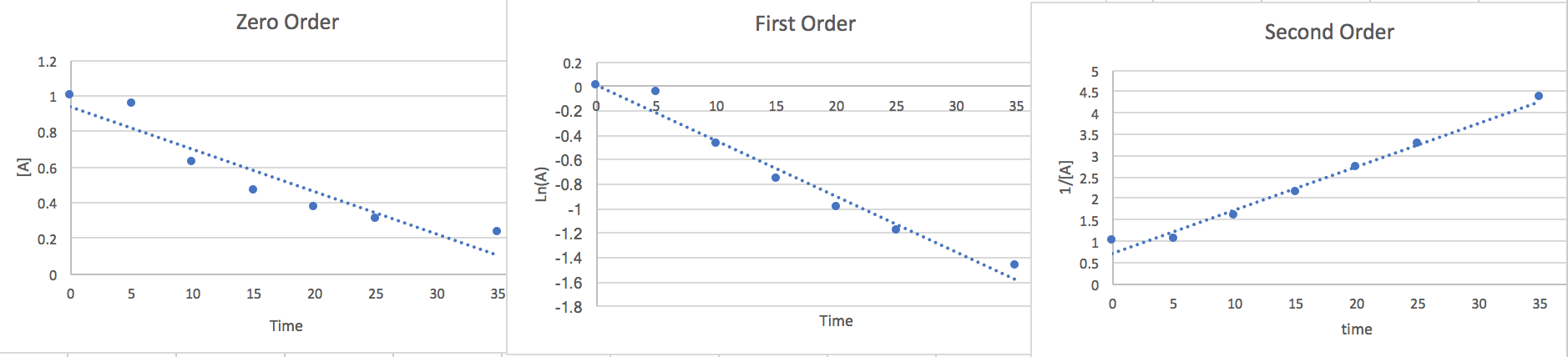
Aqui notamos que a segunda ordem é mais linear, então concluímos que a taxa é.. \[\frac{-d[A]}{2dt}=k[A]^{2}\nonumber \]Aos 15 segundos [A] =.465 e a partir da inclinação do gráfico, encontramos k=.116.então, se inserirmos esses dados e multiplicarmos os dois lados por 2 para nos livrarmos do 2 no denominador no lado esquerdo da equação, descobrimos que a taxa de desaparecimento de A é de 0,05 M/s, onde as unidades são equivalentes a [mol*L] -1 *s -1]
3.) Usando a equação,\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\) dividimos as taxas na parte a e b pela metade para obter 0,0188 M/s de 0 a 10 segundos e 0,025 M/s para a taxa instantânea estimada em 15s.
- Resposta
-
(a) taxa média, 0 − 10 s = 0,0375 mol L −1 s −1; taxa média, 12 − 18 s = 0,0225 mol L −1 s −1; (b) taxa instantânea, 15 s = 0,0500 mol L −1 s −1; (c) taxa média para formação B = 0,0188 mol L −1 s −1; taxa instantânea para formação de B = 0,0250 mol L −1 s −1
Q12.1.6
Considere a seguinte reação em solução aquosa:
\[\ce{5Br-}(aq)+\ce{BrO3-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber \]
Se a taxa de desaparecimento de Br — (aq) em um determinado momento durante a reação for 3,5 × 10 −4 M s −1, qual é a taxa de aparecimento de Br 2 (aq) naquele momento?
- Solução
-
Etapa 1. Defina a taxa da reação.
Recordar:
Para a reação geral: aA + bB → cC+ dD
\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)
Então, para a reação:\(5Br^−(aq)+BrO^−_3(aq)+6H^+→3Br_2(aq)+3H_2O(l)\)
A taxa seria:\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}=- \frac{\Delta[BrO^-_3]}{\Delta{t}}= -\frac{\Delta[H^+]}{6\Delta{t}}=\frac{\Delta[Br_2]}{3\Delta{t}}=\frac{H_2O}{3\Delta{t}}\)
Etapa 2. Uma vez que recebemos a taxa de desaparecimento de\(Br^-\) (aq) é\(3.5x10^-4 Ms^{-1}\), e queremos encontrar a taxa de aparecimento de\(Br_2\) (aq). Portanto, definimos as duas taxas iguais entre si.
\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}= \frac{\Delta[Br_2]}{3\Delta{t}}\)
E,\(-\frac{\Delta[Br^-]}{\Delta{t}}= -3.5x10^{-4} Ms^{-1}\)
Então,\(3.5x10^{-4} Ms^{-1}\) =\(\frac{5}{3}\frac{\Delta[Br_2]}{\Delta{t}}\)
Etapa 3. Agora resolva a equação.
\(\frac{(3.5x10^{-4})(3)}{5} = \frac{\Delta[Br_2]}{\Delta{t}}\)
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
- Resposta
-
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
12.2: Fatores que afetam as taxas de reação
Q12.2.1
Descreva o efeito de cada um dos seguintes na taxa de reação do magnésio metálico com uma solução de ácido clorídrico: a molaridade do ácido clorídrico, a temperatura da solução e o tamanho dos pedaços de magnésio.
- Solução
-
Molaridade do ácido clorídrico
- As taxas de reação são afetadas pela frequência com que as moléculas colidem. Alta molaridade = Alta concentração, o que significa que mais moléculas estão disponíveis para colidir, portanto, uma reação mais rápida do que aquela com baixa molaridade de HCl em um volume fixo.
- Temperaturas mais altas aumentam a taxa de reação porque as moléculas se movem mais rápido, colidindo com mais frequência.
- o aumento das temperaturas permite que mais partículas ultrapassem a barreira de energia de ativação para iniciar a reação
- a taxa de reação depende do tamanho do reagente sólido; peças menores aumentam a chance de colisão porque permitem uma área de superfície maior, portanto, uma taxa de reação mais rápida
Q12.2.2
Vá para a seção interativa Reações e Taxas PhET. Use a guia Colisão Única para representar como a colisão entre oxigênio monoatômico (O) e monóxido de carbono (CO) resulta na quebra de uma ligação e na formação de outra. Puxe o êmbolo vermelho para liberar o átomo e observe os resultados. Em seguida, clique em “Reload Launcher” e mude para “Tiro angular” para ver a diferença.
- O que acontece quando o ângulo da colisão é alterado?
- Explique como isso é relevante para a taxa de reação.
- Solução
-
De acordo com a teoria da colisão, há muitos fatores que fazem com que uma reação aconteça, com três dos fatores sendo a frequência com que as moléculas ou átomos colidem, as orientações das moléculas ou átomos e se há energia suficiente para que a reação aconteça. Portanto, se o ângulo do êmbolo for alterado, o átomo disparado (neste caso, um átomo de oxigênio solitário) atingirá a outra molécula (CO neste caso) em um ponto diferente e em um ângulo diferente, portanto, alterar a orientação e o número de colisões adequadas provavelmente não causará a ocorrência de uma reação. . Graças à simulação, podemos ver que isso é verdade: dependendo do ângulo selecionado, o átomo pode levar muito tempo para colidir com a molécula e, quando ocorre uma colisão, pode não resultar na quebra da ligação e na formação da outra (nenhuma reação acontece).
Nesse caso específico, a taxa da reação diminuirá porque, ao mudar o ângulo, as moléculas ou átomos não colidirão com a orientação correta ou, muitas vezes, com a orientação correta.
Q12.2.3
Na seção interativa de Reações e Taxas PhET, use a aba “Muitas Colisões” para observar como vários átomos e moléculas interagem sob condições variáveis. Selecione uma molécula para bombear para dentro da câmara. Defina a temperatura inicial e selecione as quantidades atuais de cada reagente. Selecione “Mostrar títulos” em Opções. Como a taxa da reação é afetada pela concentração e pela temperatura?
S12.2.3
Com base na Teoria da Colisão, uma reação só ocorrerá se as moléculas colidirem com a orientação adequada e com energia suficiente para que a reação ocorra. A energia mínima com a qual as moléculas devem colidir é chamada de energia de ativação (energia do estado de transição).
Aumentar a concentração de reagentes aumenta a probabilidade de que os reagentes colidam na orientação correta, pois há mais reagentes no mesmo volume de espaço. Portanto, aumentar a concentração de reagentes aumentaria a taxa da reação. Diminuir a concentração de reagentes diminuiria a taxa de reação porque o número total de colisões possíveis diminuiria.
A temperatura está diretamente relacionada à energia cinética das moléculas e a energia de ativação\(E_a\) é a energia mínima necessária para que uma reação ocorra e não muda para uma reação. O aumento da temperatura aumenta a energia cinética dos reagentes, o que significa que os reagentes se moverão mais rapidamente e colidirão uns com os outros com mais frequência. Portanto, aumentar a temperatura aumenta a taxa da reação. Diminuir a temperatura diminui a taxa de reação, pois as moléculas terão menos energia cinética, se moverão mais lentamente e, portanto, colidirão umas com as outras com menos frequência.
Q12.2.4
No interativo PhET Reactions & Rates, na guia Many Collisions, configure uma simulação com 15 moléculas de A e 10 moléculas de BC. Selecione “Mostrar títulos” em Opções.
- Deixe a temperatura inicial na configuração padrão. Observe a reação. A taxa de reação é rápida ou lenta?
- Clique em “Pausar” e depois em “Redefinir tudo” e, em seguida, insira 15 moléculas de A e 10 moléculas de BC mais uma vez. Selecione “Mostrar títulos” em Opções. Desta vez, aumente a temperatura inicial até que, no gráfico, a linha de energia média total esteja completamente acima da curva de energia potencial. Descreva o que acontece com a reação.
- Solução
-
a. Na simulação, selecionamos a configuração padrão e a reação A+BC. Na configuração padrão, vemos colisões frequentes, uma temperatura inicial baixa e uma energia média total menor do que a energia de ativação. A teoria da colisão afirma que a taxa de uma reação é diretamente proporcional a (a fração de moléculas com orientação necessária), (frações de colisões com energia necessária) e (frequência de colisão). Embora vejamos reagentes em movimento e colidindo com frequência, a taxa de reação direta é, na verdade, lenta porque leva muito tempo para que os produtos, AB e C, comecem a aparecer. Isso ocorre principalmente porque as frações de colisões com a energia necessária são baixas, provenientes da energia média das moléculas sendo menor do que a energia de ativação.
b. A reação prossegue em um ritmo ainda mais rápido. Novamente, a teoria da colisão afirma que a taxa de uma reação é diretamente proporcional a (a fração de moléculas com orientação necessária), (frações de colisões com energia necessária) e (frequência de colisão). Como as moléculas têm uma quantidade maior de energia, elas têm mais energia cinética. Com o aumento da energia cinética, as moléculas não só colidem mais, mas também aumentam na fração da colisão. No entanto, a reação para frente e a reação para trás ocorrem em um ritmo rápido, então ambas acontecem quase simultaneamente. Demora menos tempo para que ambas as reações aconteçam. Com as duas reações se somando em geral, eventualmente há um estado de equilíbrio. O processo no qual o equilíbrio é alcançado, no entanto, é mais rápido. Portanto, a quantidade de produtos da A+BC permanece a mesma depois de um tempo.
12.3: Leis tarifárias
Q12.3.1
Como a taxa de uma reação e sua constante de taxa diferem?
S12.3.1
A taxa de uma reação ou taxa de reação é a mudança na concentração do reagente ou do produto durante um período de tempo. Se as concentrações mudarem, a taxa também muda.
Tarifa para A → B:
A constante de taxa (k) é uma constante de proporcionalidade que relaciona as taxas de reação aos reagentes. Se as concentrações mudarem, a constante de taxa não muda.
Para uma reação com a equação geral:\(aA+bB→cC+dD \)
a lei de taxas determinada experimentalmente geralmente tem a seguinte forma:
Q12.3.2
Duplicar a concentração de um reagente aumenta a taxa de uma reação quatro vezes. Com esse conhecimento, responda às seguintes perguntas:
- Qual é a ordem da reação em relação a esse reagente?
- Triplicar a concentração de um reagente diferente aumenta a taxa de uma reação três vezes. Qual é a ordem da reação em relação a esse reagente?
- Solução
-
(a) 2; (b) 1
Q12.3.3
Triplicar a concentração de um reagente aumenta a taxa de uma reação nove vezes. Com esse conhecimento, responda às seguintes perguntas:
- Qual é a ordem da reação em relação a esse reagente?
- Aumentar a concentração de um reagente em um fator de quatro aumenta a taxa de uma reação quatro vezes. Qual é a ordem da reação em relação a esse reagente?
Q12.3.4
Quanto e em que direção cada uma das seguintes opções afetará a taxa da reação:\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) se a lei da taxa para a reação é\(\ce{rate}=k[\ce{NO2}]^2\)?
- Diminuindo a pressão de NO 2 de 0,50 atm para 0,250 atm.
- Aumentar a concentração de CO de 0,01 M para 0,03 M.
- Solução
-
(a) O processo reduz a taxa em um fator de 4. (b) Como o CO não aparece na lei de taxas, a taxa não é afetada.
Q12.3.5
Como cada uma das seguintes opções afetará a taxa da reação:\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) se a lei de taxa para a reação é\(\ce{rate}=k[\ce{NO2}][\ce{CO}]\)?
- Aumentando a pressão de NO 2 de 0,1 atm para 0,3 atm
- Aumentar a concentração de CO de 0,02 M para 0,06 M.
Q12.3.6
Os voos regulares de aeronaves supersônicas na estratosfera são preocupantes porque essas aeronaves produzem óxido nítrico, NO, como subproduto no escapamento de seus motores. O óxido nítrico reage com o ozônio, e foi sugerido que isso poderia contribuir para o esgotamento da camada de ozônio. A reação\(\ce{NO + O3⟶NO2 + O2}\) é de primeira ordem em relação ao NO e AO 3 com uma taxa constante de 2,20 × 10 7 L/mol/s. Qual é a taxa instantânea de desaparecimento do NO quando [NO] = 3,3 × 10 −6 M e [O 3] = 5,9 × 10 −7 M ?
- Solução
-
4,3 × 10 −5 mol/L/s
Q12.3.7
O fósforo radioativo é usado no estudo dos mecanismos de reação bioquímica porque os átomos de fósforo são componentes de muitas moléculas bioquímicas. A localização do fósforo (e a localização da molécula à qual ele está ligado) pode ser detectada a partir dos elétrons (partículas beta) que ele produz:
\[\ce{^{32}_{15}P⟶^{32}_{16}S + e-}\nonumber \]
Taxa = 4,85 × 10 −2\(\mathrm{day^{-1}\:[^{32}P]}\)
Qual é a taxa instantânea de produção de elétrons em uma amostra com uma concentração de fósforo de 0,0033 M?
Q12.3.8
A constante de taxa para o decaimento radioativo de 14 C é 1,21 × 10 −4 ano −1. Os produtos da decomposição são átomos de nitrogênio e elétrons (partículas beta):
\[\ce{^6_{14}C⟶^{6}_{14}N + e-}\nonumber \]
\[\ce{rate}=k[\ce{^6_{14}C}]\nonumber \]
Qual é a taxa instantânea de produção de átomos de N em uma amostra com um teor de carbono-14 de 6,5 × 10 −9 M?
- Solução
-
7,9 × 10 −13 mol/L/ano
Q12.3.9
Qual é a taxa instantânea de produção de N átomos Q12.3.8 em uma amostra com um teor de carbono-14 de 1,5 × 10 −9 M?
Q12.3.10
A decomposição do acetaldeído é uma reação de segunda ordem com uma taxa constante de 4,71 × 10 −8 L/mol/s. Qual é a taxa instantânea de decomposição do acetaldeído em uma solução com uma concentração de 5,55 × 10 −4 M?
Q12.3.11
O álcool é removido da corrente sanguínea por uma série de reações metabólicas. A primeira reação produz acetaldeído; em seguida, outros produtos são formados. Os dados a seguir foram determinados para a taxa na qual o álcool é removido do sangue de um homem comum, embora as taxas individuais possam variar de 25 a 30%. As mulheres metabolizam o álcool um pouco mais lentamente do que os homens:
| [C 2 H 5 OH] (M) | 4,4 × 10 −2 | 3,3 × 10 −2 | 2,2 × 10 −2 |
|---|---|---|---|
| Taxa (mol/L/h) | 2,0 × 10 −2 | 2,0 × 10 −2 | 2,0 × 10 −2 |
Determine a equação da taxa, a constante da taxa e a ordem geral dessa reação.
- Solução
-
taxa = k; k = 2,0 × 10 −2 mol/L/h (cerca de 0,9 g/L/h para o homem médio); A reação é de ordem zero.
Q12.3.12
Sob certas condições, a decomposição da amônia em uma superfície metálica fornece os seguintes dados:
| [NH 3] (M) | 1,0 × 10 −3 | 2,0 × 10 −3 | 3,0 × 10 −3 |
|---|---|---|---|
| Taxa (mol/L/h 1) | 1,5 × 10 −6 | 1,5 × 10 −6 | 1,5 × 10 −6 |
Determine a equação da taxa, a constante da taxa e a ordem geral dessa reação.
Q12.3.13
O cloreto de nitrosilo, NOCl, se decompõe em NO e Cl 2.
\[\ce{2NOCl}(g)⟶\ce{2NO}(g)+\ce{Cl2}(g)\nonumber \]
Determine a equação da taxa, a constante da taxa e a ordem geral dessa reação a partir dos seguintes dados:
| [NoCl] (M) | 0,10 | 0,20 | 0,30 |
|---|---|---|---|
| Taxa (mol/L/h) | 8,0 × 10 −10 | 3,2 × 10 −9 | 7,2 × 10 −9 |
- Solução
-
Antes de podermos descobrir a constante da taxa, primeiro devemos determinar a equação básica da taxa e a ordem da taxa. A equação básica da taxa para esta reação, onde n é a ordem da taxa de NoCl e k é a constante da taxa, é
\[rate = k[NOCl]^n\nonumber \]
já que o NoCl é o reagente na reação.
Para descobrir a ordem da reação, precisamos encontrar a ordem de [NoCl], pois é o único reagente na reação. Para fazer isso, devemos examinar como a taxa da reação muda à medida que a concentração de NOCl muda.
À medida que [NoCl] dobra na concentração de 0,10 M para 0,20 M, a taxa vai de 8,0 x 10 -10 para 3,2 x 10 -9
(3,2 x 10 -9 (mol/L/h))/(8,0 x 10 -10 (mol/L/h)) = 4
então concluímos que, à medida que [NoCl] dobra, a taxa aumenta em 4. Como 2 2 = 4, podemos dizer que a ordem de [NoCl] é 2, então nossa lei de tarifas atualizada é
\[rate = k[NOCl]^2\nonumber \]
Agora que temos a ordem, podemos substituir os primeiros valores experimentais da tabela dada para encontrar a constante de taxa, k
(8,0 x 10 -10 (mol/L/h)) = k (0,10 M) 2 so
\[k= \dfrac{8.0 \times 10^{-10}}{ (0.10\, M)^2} = 8 \times 10^{-8} M^{-1} sec^{-1}\nonumber \]
Conseguimos encontrar as unidades de k usando a ordem da taxa, quando a ordem da taxa é 2 unidades de k são M -1 x sec -1
Portanto, a equação da taxa é: taxa = k [NoCl] 2, é de segunda ordem e k = 8 x 10 -8 M -1 x sec -1
Lei geral de taxas:\[rate = \underbrace{(8 \times 10^{-8})}_{\text{1/(M x sec)}} [NOCl]^2\nonumber \]
- Resposta
-
taxa = k [NoCl] 2; k = 8,0 × 10 −8 L/mol/s; segunda ordem
Q12.3.14
A partir dos dados a seguir, determine a equação da taxa, a constante da taxa e a ordem em relação a A para a reação\(A⟶2C\).
| [A] (M) | 1,33 × 10 −2 | 2,66 × 10 −2 | 3,99 × 10 −2 |
|---|---|---|---|
| Taxa (mol/L/h) | 3,80 × 10 −7 | 1,52 × 10 −6 | 3,42 × 10 −6 |
- Solução
-
A. Usando os dados experimentais, podemos comparar os efeitos da mudança [A] na taxa de reação relacionando proporções de [A] com proporções de taxas
\[ \frac{2.66 \times 10^{-2}}{1.33 \times 10^{-2}} = 2\nonumber \]e\[ \frac{1.52 \times 10^{-6}}{3.8 \times 10^{-7}} = 4\nonumber \]
B. A partir disso, sabemos que dobrar a concentração de A resultará na quadruplicação da taxa de reação. A ordem dessa reação é 2.
C. Agora podemos escrever a equação da taxa, pois sabemos a ordem:
\[rate=k[A]^2\nonumber \]
D. Ao inserir um conjunto de dados experimentais em nossa equação de taxa, podemos resolver a constante de taxa, k:
\[3.8 \times 10^{-7} = k \times (1.33 \times 10^{-2})^{2}\nonumber \]
\[k = \frac{3.8 \times 10^{-7}}{1.769 \times 10^{-4}}\nonumber \]
\[k= .00215 M^{-1}s^{-1}\nonumber \]
- Resposta
-
\(k= .00215 M^{-1}s^{-1}\)
2ª ordem
Q12.3.15
O óxido de nitrogênio (II) reage com o cloro de acordo com a equação:
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\nonumber \]
As seguintes taxas iniciais de reação foram observadas para certas concentrações de reagentes:
| [NÃO] (mol/L 1) | [Cl 2] (mol/L) | Taxa (mol/L/h) |
|---|---|---|
| 0,50 | 0,50 | 1,14 |
| 1,00 | 0,50 | 4,56 |
| 1,00 | 1,00 | 9,12 |
Qual é a equação da taxa que descreve a dependência da taxa nas concentrações de NO e Cl 2? Qual é a constante de taxa? Quais são as ordens em relação a cada reagente?
- Solução
-
Para a equação geral,
\(aA + bB \rightarrow cC + dD\)
A taxa pode ser escrita como
\(rate = k[A]^{m}[B]^{n}\)onde k é a constante de taxa e m e n são as ordens de reação.
Para nossa equação
\(2NO(g) + Cl_{2}(g) \rightarrow 2NOCl(g)\)
o\(rate = k[NO]^{m}[Cl_{2}]^{n}\)
Agora, precisamos encontrar as ordens de reação. As ordens de reação só podem ser encontradas por meio de valores experimentais. Podemos comparar duas reações em que um dos reagentes tem a mesma concentração para os dois ensaios e resolver a ordem da reação.
\(\frac{rate_{1}}{rate_{2}}=\frac{[NO]_{1}^{m}[Cl_{2}]_{1}^{n}}{[NO]_{2}^{m}[Cl_{2}]_{2}^{n}}\)
Podemos usar os dados na tabela fornecida. Se inserirmos os valores das linhas 1 e 2, veremos que os valores para a concentração de Cl serão cancelados, restando apenas as taxas e as concentrações de NO.
\(\frac{1.14}{4.56}=\frac{[0.5]^{m}}{[1.0]^{m}}\)
Agora podemos resolver para m e descobrimos que m =2. Isso significa que a ordem de reação para [NO] é 2.
Agora precisamos encontrar o valor de n. Para fazer isso, podemos usar a mesma equação, mas com os valores das linhas 2 e 3. Desta vez, a concentração de NO será cancelada.
\(\frac{4.56}{9.12}=\frac{[0.5]^{n}}{[1.0]^{n}}\)
Quando resolvemos para n, descobrimos que n = 1. Isso significa que a ordem de reação para [Cl 2] é 1.
Estamos um passo mais perto de terminar nossa equação de taxa.
\(rate = k[NO]^{2}[Cl_{2}]\)
Finalmente, podemos resolver a constante de taxa. Para fazer isso, podemos usar um dos ensaios do experimento e inserir os valores da taxa e das concentrações dos reagentes e, em seguida, resolver k.
\(1.14 mol/L/h = k[0.5 mol/L]^{2}[0.5mol/L]\)
\(k=9.12L^{2}mol^{-2}h^{-1}\)
Então, nossa equação de taxa final é:
\(rate = (9.12 L^{2} mol^{-2}h^{-1})[NO]^{2}[Cl_{2}]\)
*Um erro comum é esquecer as unidades. Certifique-se de rastrear suas unidades durante todo o processo de determinação de sua taxa constante. Tenha cuidado porque as unidades mudarão em relação à ordem da reação.
- Resposta
-
taxa = k [NO] 2 [Cl] 2; k = 9,12 L 2 mol −2 h −1; segunda ordem em NO; primeira ordem em Cl 2
Q12.3.17
O hidrogênio reage com o monóxido de nitrogênio para formar monóxido de dinitrogênio (gás do riso) de acordo com a equação:
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g)\nonumber \]
Determine a equação da taxa, a constante de taxa e as ordens em relação a cada reagente a partir dos seguintes dados:
| [NÃO] (M) | 0,30 | 0,60 | 0,60 |
|---|---|---|---|
| [H 2] (M) | 0,35 | 0,35 | 0,70 |
| Taxa (mol/L/s) | 2,835 × 10 −3 | 1,134 × 10 −2 | 2,268 × 10 −2 |
- Solução
-
Determine a equação da taxa, a constante da taxa e as ordens em relação a cada reagente.
A constante de taxa e os pedidos podem ser determinados por meio da lei de taxa diferencial. A forma geral da lei da taxa diferencial é dada abaixo:
aA + bB + cC => produtos
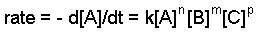
onde A, B e C são as concentrações dos reagentes, k é a taxa constante e n, m e p se referem à ordem de cada reagente.
Para encontrar as ordens de cada reagente, vemos que quando [NO] dobra, mas [H 2] não muda, a taxa quadruplica, o que significa que [NÃO] é uma reação de segunda ordem ([NO] 2). Quando [H 2] dobra, mas [NO] não muda, a taxa dobra, o que significa que [H 2] é uma reação de primeira ordem. Portanto, a lei de taxas seria mais ou menos assim:
Taxa = k [NO] 2 [H 2]
Podemos usar essa lei de taxa para determinar o valor da constante de taxa. Insira os dados de concentração e taxa do reagente de um dos ensaios para resolver k a constante de taxa. Nesse caso, optamos por usar os dados da tentativa 1 da segunda coluna da tabela de dados.
2,835x10 -3 = k [0,3] 2 [0,35]
k = 0,09 M -2 /s -1
Q12.3.18
Para a reação\(A⟶B+C\), os seguintes dados foram obtidos a 30 °C:
| [A] (M) | 0,230 | 0,356 | 0,557 |
|---|---|---|---|
| Taxa (mol/L/s) | 4,17 × 10 −4 | 9,99 × 10 −4 | 2,44 × 10 −3 |
- Qual é a ordem da reação em relação a [A] e qual é a equação da taxa?
- Qual é a constante de taxa?
- Solução
-
1. A equação de taxa para uma reação de\(n\) ordem é dada como\(\frac{dr}{dt}={k}{[A]^n}\). Onde\([A]\) está a concentração em M e\(\frac{dr}{dt}\) é a taxa em M/s.
Podemos então usar cada conjunto de pontos de dados, inserir seus valores na equação da taxa e resolver\(n\). Observe que você pode usar qualquer um dos pontos de dados, desde que a concentração corresponda à sua taxa.
Equação de taxa 1:\(4.17 \times {10}^{-4}={k}{[0.230]^n}\)
Equação de taxa 2:\(9.99 \times {10}^{-4}={k}{[0.356]^n}\)
Dividimos a equação de taxa 1 pela equação de taxa 2 para cancelar k, a constante de taxa.
\({\frac{4.17 \times {10}^{-4}}{9.99 \times {10}^{-4}}} = {\frac{k[0.230]^n}{k[0.356]^n}} \)
\({0.417}={0.646^n}\)
Agora, a única incógnita que temos é\(n\). Usando regras de logaritmo, pode-se resolver isso.
\(ln{\: 0.417}={n \cdot ln{\: 0.646}}\)
\(\frac{ln{\: 0.417}}{ln{\:0.646}}=n=2\)
A equação da taxa é de segunda ordem em relação a A e é escrita como\(\frac{dr}{dt}={k}{[A]^2}\).
2. Podemos resolver isso\(k\) inserindo qualquer ponto de dados em nossa equação de taxa\(\frac{dr}{dt}={k}{[A]^2}\).
Usando os primeiros pontos de dados, por exemplo,\( \frac{dr}{dt} = 4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}\) [\( [A]=0.230 \:\frac{mol}{L}\)e] obtemos a equação.\(4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}={k}{[0.230 \:\frac{mol}{L}]^2}\)
O que resolve\(k=7.88 \times {10}^{-3} \frac{L}{mol \cdot s}\)
Como sabemos que essa é uma reação de segunda ordem, as unidades apropriadas para também\(k\) podem ser escritas como\( \frac{1}{M \cdot s}\)
- Resposta
-
(a) A equação da taxa é de segunda ordem em A e é escrita como taxa = k [A] 2. (b) k = 7,88 × 10 −13 L mol −1 s −1
Q12.3.19
Para a reação\(Q⟶W+X\), os seguintes dados foram obtidos a 30 °C:
| [Q] inicial (M) | 0,170 | 0,212 | 0,357 |
|---|---|---|---|
| Taxa (mol/L/s) | 6,68 × 10 −3 | 1,04 × 10 −2 | 2,94 × 10 −2 |
- Qual é a ordem da reação em relação a [Q] e qual é a equação da taxa?
- Qual é a constante de taxa?
- Solução
-
Qual é a ordem da reação em relação a [Q] e qual é a equação da taxa?
- Reação do pedido: 2 porque quando você usa o teste de proporção 3:2, ela ficará assim:
- (\(\dfrac{2.94*10^{-2}}{1.04*10^{-2}}\)) = (\(\dfrac{0.357^{x}}{0.212^{x}}\))
- 2,82 = 1,7 x
- x = 2 então a ordem da reação é 2
- Equação de taxa de reação: Taxa = K [Q] 2
- Para encontrar a constante de taxa (k), basta inserir e calcular um dos ensaios na equação da taxa
- 1,04 x 10 -2 =k [0,2122]
- k=0,231\(M^{-1}s^{-1}\)
- Resposta
-
Pedido: 2
k=0,231\(M^{-1}s^{-1}\)
Q12.3.20
A taxa constante para a decomposição de primeira ordem a 45 °C do pentóxido de dinitrogênio, N 2 O 5, dissolvido em clorofórmio, CHCl 3, é 6,2 × 10 −4 min −1.
\[\ce{2N2O5⟶4NO2 + O2}\nonumber \]
Qual é a taxa da reação quando [N 2 O 5] = 0,40 M?
- Solução
-
Etapa 1: O primeiro passo é escrever a lei de taxas. Conhecemos a fórmula geral para uma lei de taxas de primeira ordem. É o seguinte: Taxa=K [A]
Etapa 2: Agora conectamos [N 2 O 5] para [A] em nossa lei geral de taxas. Também inserimos nossa constante de taxa (k), que nos foi dada. Agora, nossa equação tem a seguinte aparência:
Taxa = (6,2x10 -4 min -1) [N 2 O 5]
Etapa 3: Agora conectamos nossa molaridade dada. [N 2 O 5] =0,4 M. Agora, nossa equação é a seguinte:
Tarifa = (6,2x10 -4 min -1) (0,4 M)
Etapa 4: Agora resolvemos nossa equação. Tarifa = (6,2x10 -4 min -1) (0,4 M) = 2,48x10 -4 M/min.
Etapa 5: Use números significativos e conversão de unidades para arredondar 2,48x10 -4 M/min para 2,5 × 10 −4 (moles) L -1 min -1
- Resposta
-
(a) 2,5 × 10 −4 mol/L/min
Q12.3.21
A produção anual de HNO 3 em 2013 foi de 60 milhões de toneladas métricas. A maior parte foi preparada pela seguinte sequência de reações, cada uma executada em um recipiente de reação separado.
- \(\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\)
- \(\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\)
- \(\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\)
A primeira reação é realizada pela queima de amônia no ar sobre um catalisador de platina. Essa reação é rápida. A reação na equação (c) também é rápida. A segunda reação limita a taxa na qual o ácido nítrico pode ser preparado a partir da amônia. Se a equação (b) é de segunda ordem em NO e primeira ordem em O 2, qual é a taxa de formação de NO 2 quando a concentração de oxigênio é 0,50 M e a concentração de óxido nítrico é 0,75 M? A constante de taxa para a reação é 5,8 × 10 −6 L 2 /mol 2 /s.
- Solução
-
Para determinar a lei de taxas de uma equação, precisamos observar seu passo lento. Como as equações a e c são rápidas, a equação b pode ser considerada a etapa lenta da reação. A etapa lenta também é considerada a etapa determinante da taxa do sistema.
Portanto, a etapa de determinação da taxa é a segunda etapa porque é a etapa lenta.
taxa de produção de\(NO_2 = k [A]^m [B]^n \)
\(rate = k [NO]^2 [O_2]^1~M/s\)
\(rate = (5.8*10^{-6}) [0.75]^2 [0.5]^1 ~M/s\)
\(rate = 1.6*10^{-6}~M/s\)
- Resposta
-
\(rate = 1.6*10^{-6}~M/s\)
Q12.3.22
Os seguintes dados foram determinados para a reação:
\[\ce{I- + OCl- ⟶ IO- + Cl-}\nonumber \]
| 1 | 2 | 3 | |
|---|---|---|---|
| \(\mathrm{[I^-]_{initial}}\)(M) | 0,10 | 0,20 | 0,30 |
| \(\mathrm{[OCl^-]_{initial}}\)(M) | 0,050 | 0,050 | 0,010 |
| Taxa (mol/L/s) | 3,05 × 10 −4 | 6,20 × 10 −4 | 1,83 × 10 −4 |
Determine a equação da taxa e a constante da taxa para essa reação.
- Solução
-
Usando os reagentes, podemos formar a lei da taxa da reação: $ r=k [OCl^-] ^n [I^-] ^m\]
A partir daí, precisamos usar os dados para determinar a ordem de ambos\([OCl^-]\)\([I^-]\) e. Ao fazer isso, precisamos\(r_1\) comparar com\(r_2\) algo que:
\[ \frac {r_1}{r_2} = \frac {(0.10^m)(0.050^n)}{(0.20^m)(0.050^n)} = \frac {3.05 \times 10^{-4}}{6.20 \times 10^{-4}} \]
\[ 0.5^m = 0.5 \]
\[ m = 1 \]
Podemos “riscar” a concentração de\([OCl^-]\) porque ela tem a mesma concentração em ambos os ensaios usados.
Agora que sabemos que m (\([I^-]\)) tem uma primeira ordem de 1.
Não podemos “riscar”\([I^-]\) a descoberta\([OCl^-]\) porque não há duas provações com a mesma concentração. Para resolver para n, conectaremos 1 para m.
\[ \frac {r_1}{r_3} = \frac {(0.10^{1})(0.050^n)}{(0.30^{1})(0.010^n)} = \frac {3.05 \times 10^{-4}}{1.83 \times 10^{-4}} \]
\[ \frac {1}{3} (5^{n}) = 1.6666667 \]
\[ 5^{n} = 5 \]
\[ n = 1 \]
Como sabemos que as ordens de n e m são iguais a um, não podemos substituí-las na equação da lei da taxa junto com as respectivas concentrações (da primeira, segunda ou terceira reação) e resolver a constante de taxa, k.
\[ r=k[OCl^-]^n[I^-]^m \]
\[ 3.05 * 10^{-4}= k[0.05]^1[0.10]^1 \]
\[ k = 6.1 * 10^{-2} \frac {L}{mol \times s} \]
Assim, a lei geral da taxa é: $ r = (6.1 * 10^ {-2}\ frac {L} {mol\ times s}) [OCl^-] [I^-]\]
As unidades para K dependem da ordem geral da reação. Para encontrar a ordem geral, adicionamos m e n juntos. Ao fazer isso, encontramos uma ordem geral de 2. É por isso que as unidades para K são $\ frac {L} {mol\ times s}\]
- Resposta
-
taxa = k [I −] [OCl −1]; k = 6,1 × 10 −2 L mol −1 s −1
Q12.3.23
Na reação
\[2NO + Cl_2 → 2NOCl\nonumber \]
os reagentes e produtos são gases à temperatura da reação. Os seguintes dados de taxa foram medidos para três experimentos:
| p inicial {NÃO} | P inicial {Cl 2} | Taxa inicial |
|---|---|---|
| (caixa eletrônico) | (caixa eletrônico) | (moles de A consumidos atm sec -1) |
| 0,50 | 0,50 | 5,1 x 10 -3 |
| 1,0 | 1,0 | 4,0 x 10 -2 |
| 0,50 | 1,0 | 1,0 x 10 -2 |
- A partir desses dados, escreva a equação da taxa para essa reação gasosa. Qual é a ordem da reação em NO, Cl 2 e em geral?
- Calcule a constante de taxa específica para essa reação.
- Solução
-
a. A equação da taxa pode ser determinada projetando experimentos que medem a (s) concentração (ões) de um ou mais reagentes ou produtos em função do tempo. Para a reação\(A+B\rightarrow products\), por exemplo, precisamos determinar k e os expoentes m e n na seguinte equação:
\[rate=k[A]^m[B]^n\nonumber \]
Para fazer isso, a concentração inicial de B pode ser mantida constante enquanto se varia a concentração inicial de A e calculando a taxa de reação inicial. Essa informação deduziria a ordem da reação em relação a A. O mesmo processo pode ser feito para encontrar a ordem da reação
em relação a B. Neste exemplo específico,
\[\frac{rate_2}{rate_3}=\frac{k[A_2]^m[B_2]^n}{k[A_3]^m[B_3]^n}\nonumber \]
então, tomando os valores da tabela,
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{k[1.0]^m[1.0]^n}{k[0.5]^m[1.0]^n}\nonumber \]
e ao cancelar termos semelhantes, você fica com
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{[1.0]^m}{[0.5]^m}\nonumber \]
Agora, resolva para m
\(4=2^m\Longrightarrow m=2\) Porque m=2, a reação em relação a\(NO\) é 2. \(NO\)é de segunda ordem.
Você pode repetir o mesmo processo para encontrar n.
\[\frac{rate_3}{rate_1}=\frac{k[A_3]^m[B_3]^n}{k[A_1]^m[B_1]^n}\nonumber \]
Tomando os valores da tabela
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{k[0.5]^m[1.0]^n}{k[0.5]^m[0.5]^n}\nonumber \]
e cancelando termos semelhantes, você fica com
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{[1.0]^n}{[0.5]^n}\nonumber \]
Agora, desta vez, resolva para n
\(2=2^n\Longrightarrow n=1\)
Porque n=1, a reação em relação a\(Cl_2\) é 1. \(Cl_2\)é o primeiro pedido.
Portanto, a equação da taxa é:\[rate=k[NO]^2[Cl_2]^1\nonumber \]
Para encontrar a ordem geral da taxa, basta adicionar os pedidos. Segunda ordem + primeira ordem torna a reação geral em terceira ordem.b. A constante de taxa é calculada inserindo os dados de qualquer linha da tabela na lei de taxas determinada experimentalmente e resolvendo k. Para uma reação de terceira ordem, as unidades de k são\(frac{1}{atm^2*sec}\). Usando o Experimento 1,
\[rate=k[NO]^2[Cl_2]^1\Longrightarrow 5.1*10^{-3} \frac{atm}{sec}=k[0.5m atm]^2[0.5 atm]^1\nonumber \]
\[k=0.0408 \frac{1}{atm^2*sec}\nonumber \]
- Resposta
-
\(NO\)é de segunda ordem.
\(Cl_2\)é o primeiro pedido.
A ordem geral da reação é três.
b)
\(k=0.0408\; atm^{-2}*sec^{-1}\)
12.4: Leis tarifárias integradas
Q12.4.1
Descreva como os métodos gráficos podem ser usados para determinar a ordem de uma reação e sua constante de taxa a partir de uma série de dados que inclui a concentração de A em momentos variáveis.
- Solução
-
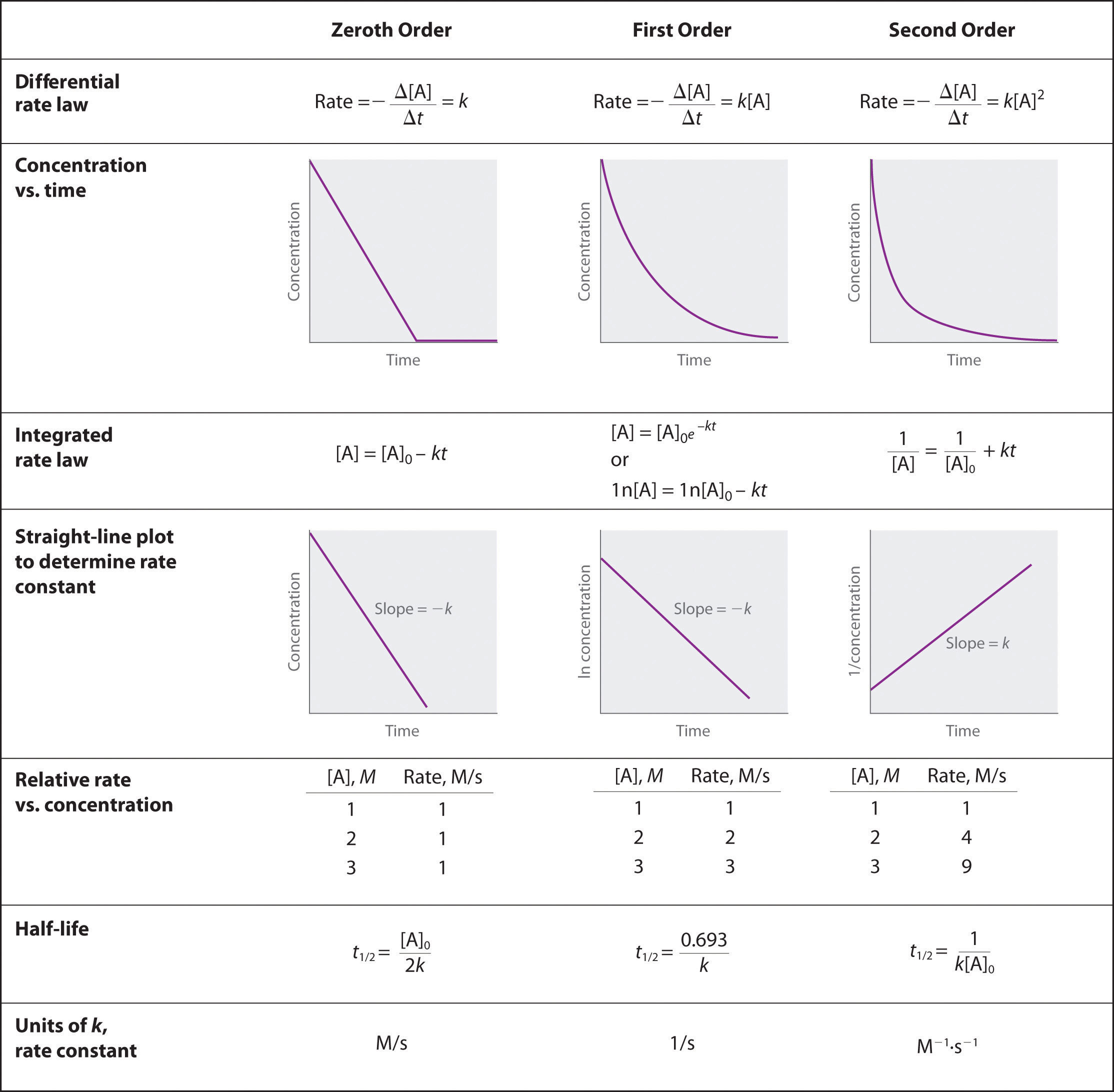
Para determinar a ordem de uma reação quando dada a série de dados, deve-se representar graficamente os dados como eles estão, representá-los graficamente como logaritmo natural de [A] e representá-los graficamente como 1/ [A]. Qualquer método que produza uma linha reta determinará a ordem. Respectivamente aos métodos de representação gráfica acima, se uma linha reta é produzida pelo primeiro método gráfico, é uma ordem 0, se pelo segundo método é uma 1ª ordem e o terceiro método gráfico é uma 2ª ordem. Quando a ordem do gráfico é conhecida, uma série de equações, dadas na imagem acima, pode ser usada com os vários pontos no gráfico para determinar o valor de k. Podemos ver que precisamos de um valor inicial de A e um valor final de A, e ambos seriam dados pelos dados.
Ordem zero ao traçar a concentração inicial versus a concentração final, você tem uma inclinação linear negativa.
\[[A] = [A]_0 − kt\nonumber \]
Primeira ordem ao traçar ln [concentração inicial] versus ln [concentração final], você tem uma inclinação linear negativa.
\[\ln[A] = \ln[A]_0 − kt\nonumber \]
Segunda ordem ao traçar a 1/ [concentração inicial] versus 1/ [concentração final], você tem uma inclinação linear positiva.
\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt\nonumber \]
Q12.4.2
Use os dados fornecidos para determinar graficamente a constante de ordem e taxa da seguinte reação:\(\ce{SO2Cl2 ⟶ SO2 + Cl2}\)
| Hora (s) | 0 | 5,00 × 10 3 | 1,00 × 10 4 | 1,50 × 10 4 | 2,50 × 10 4 | 3,00 × 10 4 | 4,00 × 10 4 |
|---|---|---|---|---|---|---|---|
| [SO 2 Cl 2] (M) | 0,100 | 0,0896 | 0,0802 | 0,0719 | 0,0577 | 0,0517 | 0,0415 |
- Solução
-
Use os dados para determinar graficamente a constante de ordem e taxa da seguinte reação.
Para determinar a lei de taxa para uma reação a partir de um conjunto de dados que consiste em concentração (ou os valores de alguma função de concentração) versus tempo, faça três gráficos dos dados com base nas leis de taxa integradas de cada reação de ordem.
[concentração] versus tempo (linear para uma reação de ordem zero) ln [concentração] versus tempo (linear para uma reação de 1ª ordem) 1/[concentração] versus tempo (linear para uma reação de 2ª ordem)inclinação = -2,0 x 10 -5
k = 2,0 x 10 -5
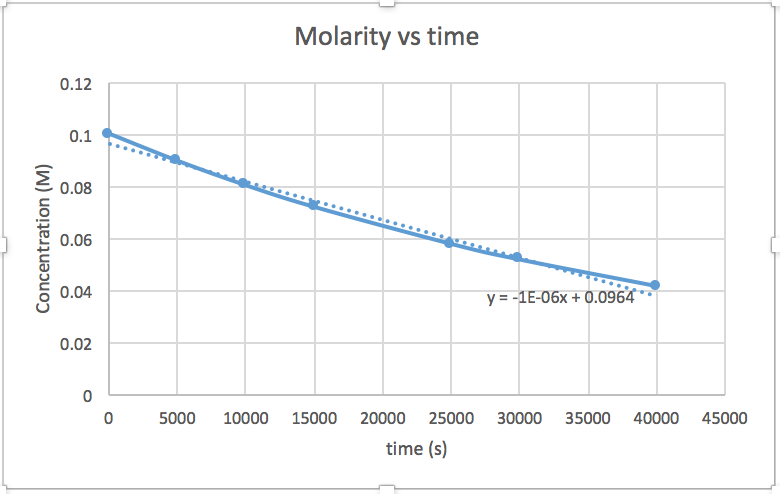
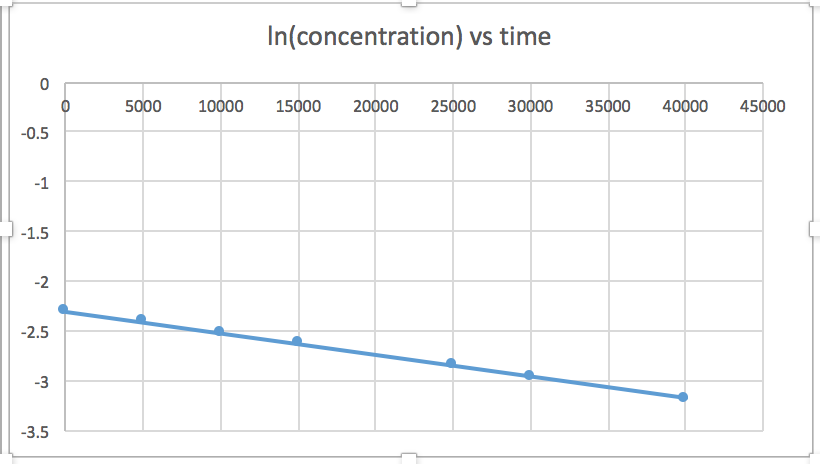
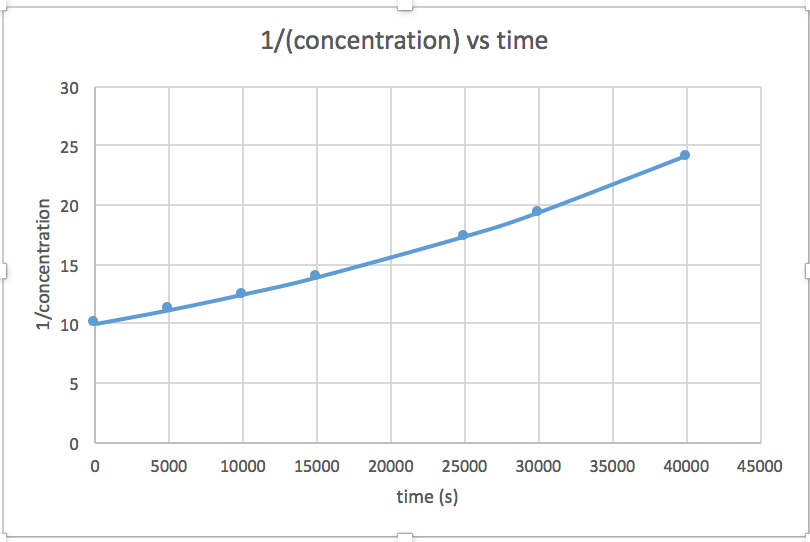
O gráfico linear indica a ordem da reação. Em seguida, você pode encontrar a equação de taxa correta:
reação de ordem zero taxa = k (k = - inclinação da linha) Reação de 1ª ordem taxa = k [A] (k = - inclinação da linha) Reação de 2ª ordem taxa = k [A] 2 (k = inclinação da linha) Neste gráfico, ln (concentração) versus tempo é linear, indicando que a reação é de primeira ordem.
k = -inclinação da linha
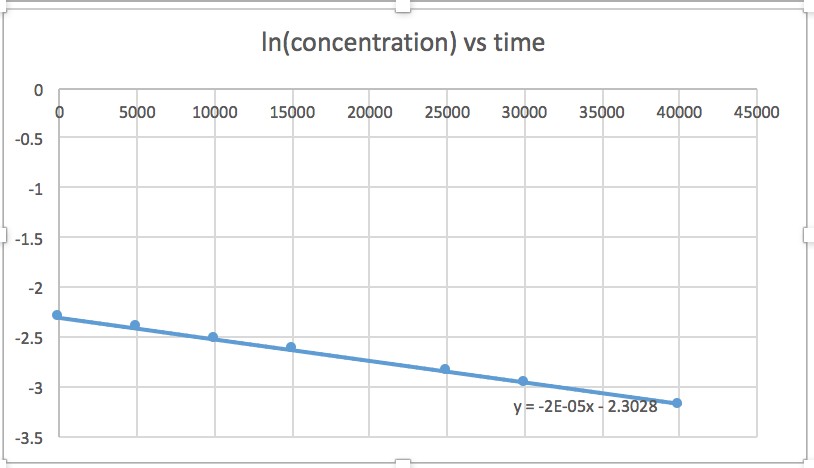
- Resposta
-
Traçar um gráfico de ln [SO 2 Cl 2] versus t revela uma tendência linear; portanto, sabemos que essa é uma reação de primeira ordem:
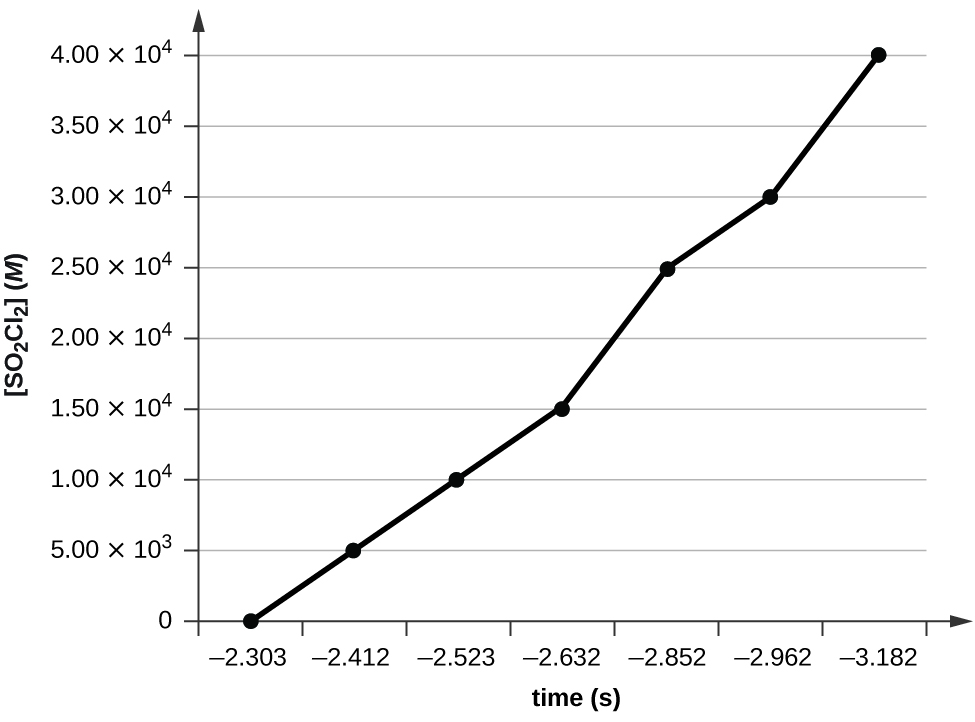
k = −2,20 × 10 5 s −1
Q12.4.3
Use os dados fornecidos em um método gráfico para determinar a constante de ordem e taxa da seguinte reação:
\[2P⟶Q+W\nonumber \]
| Hora (s) | 9.0 | 13,0 | 18,0 | 22,0 | 25,0 |
|---|---|---|---|---|---|
| [P] (M) | 1,077 × 10 −3 | 1,068 × 10 −3 | 1,055 × 10 −3 | 1,046 × 10 −3 | 1,039 × 10 −3 |
- Solução
-
Adicione textos aqui. Não exclua esse texto primeiro.
Q12.4.4
O ozônio puro se decompõe lentamente em oxigênio,\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Use os dados fornecidos em um método gráfico e determine a constante de ordem e taxa da reação.
| Tempo (h) | 0 | 2,0 × 10 3 | 7,6 × 10 3 | 1,23 × 10 4 | 1,70 × 10 4 | 1,70 × 10 4 |
|---|---|---|---|---|---|---|
| [O 3] (M) | 1,00 × 10 −5 | 4,98 × 10 −6 | 2,07 × 10 −6 | 1,39 × 10 −6 | 1,2 × 10 −6 | 1,05 × 10 −6 |
- Solução
-
Para determinar a constante de ordem e taxa, você precisa representar graficamente os dados de ordem zero, primeira ordem e segunda ordem representando a concentração versus tempo- [A] versus tempo, logaritmo natural (ln) de [A] versus tempo e 1/ [A] versus tempo, respectivamente. A ordem da reação é determinada identificando qual desses três gráficos produz uma linha reta. A constante de taxa k é representada pela inclinação do gráfico. Os gráficos com seus respectivos valores de dados seriam
Hora (s) 9.0 13,0 18,0 22,0 25,0 [P] (M) 1,077 × 10−3 1,068 × 10−3 1,055 × 10−3 1,046 × 10−3 1,039 × 10−3 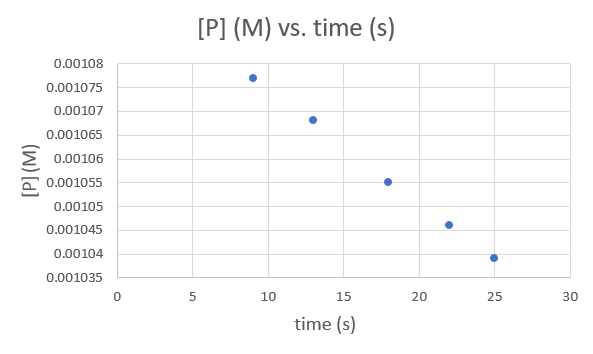.png)
Hora (s) 9.0 13,0 18,0 22,0 25,0 em [P] (M) -6.83358 -6.84197 -6.85421 -6.86278 -6.8695 .png)
Hora (s) 9.0 13,0 18,0 22,0 25,0 1/ [P] (M) 928.5051 936.3296 947.8673 956.0229 962.4639 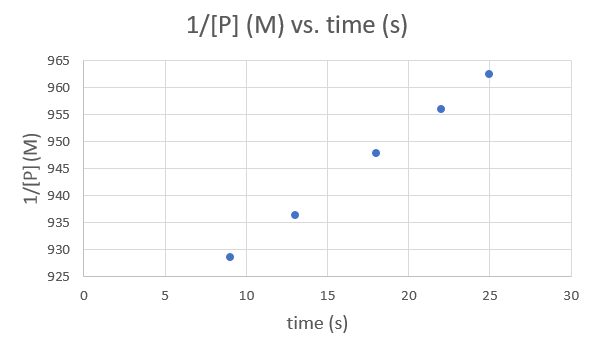.png)
Como cada gráfico produz uma linha reta, a ordem e a constante de taxa da reação não podem ser determinadas.
Identificar como as concentrações mudam em função do tempo, é necessário resolver a equação diferencial apropriada (ou seja, a lei da taxa diferencial).
A lei da taxa de ordem zero prevê um declínio linear da concentração com
o tempo A lei da taxa de 1ª ordem prevê um declínio exponencial da concentração com
o tempo A lei da taxa de 2ª ordem prevê uma queda recíproca da concentração com o tempo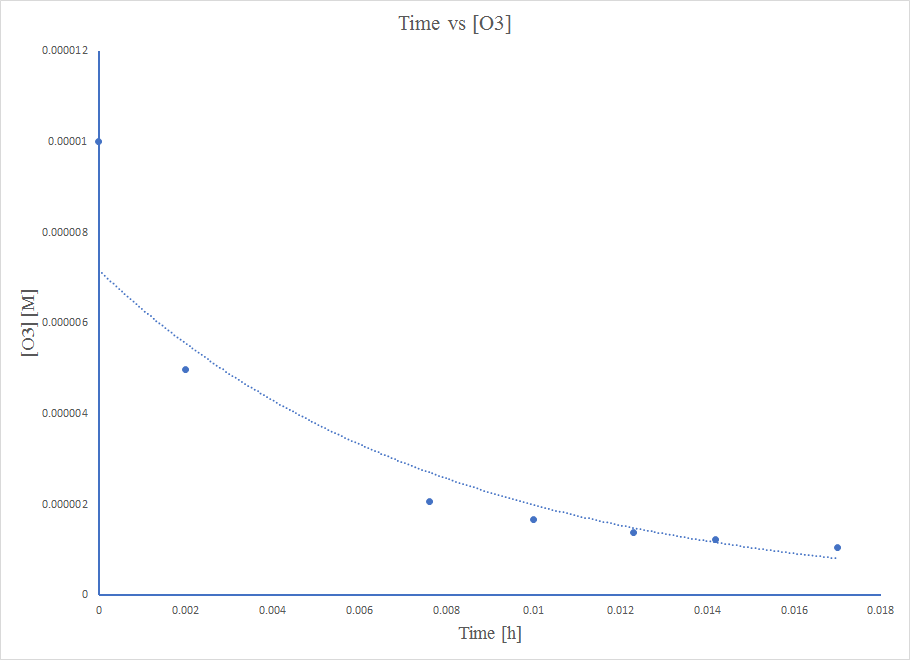
O gráfico não é linear, então a reação não é de ordem zero.

O gráfico não é linear, então a reação não é de primeira ordem.
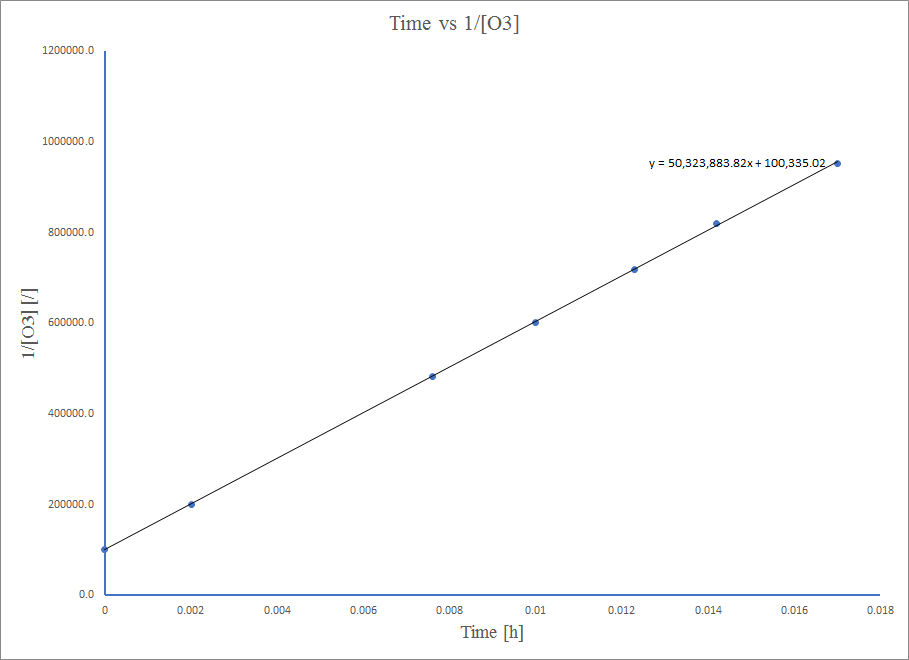
O gráfico é bem linear, então a reação é de segunda ordem.
Para uma equação de segunda ordem,\( 1/[A] \ = k*t + 1/[A_0] \)
Assim, o valor de K é a inclinação do gráfico Time vs\( \frac{1}{\ce{O3}}\),
k = 50,3*10^6 L mol −1 h −1
- Resposta
-
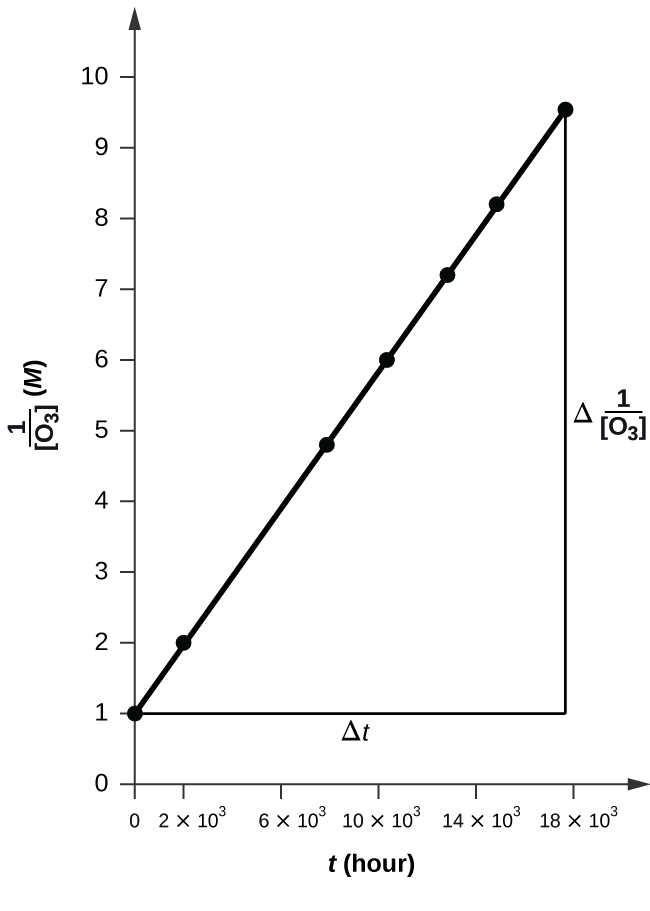
O gráfico é bem linear, então a reação é de segunda ordem.
k = 50,1 L mol −1 h −1
Q12.4.5
A partir dos dados fornecidos, use um método gráfico para determinar a constante de ordem e taxa da seguinte reação:
\[2X⟶Y+Z\]
| Hora (s) | 5,0 | 10,0 | 15,0 | 20,0 | 25,0 | 30,0 | 35,0 | 40,0 |
|---|---|---|---|---|---|---|---|---|
| [X] (M) | 0,0990 | 0,0497 | 0,0332 | 0,0249 | 0,0200 | 0,0166 | 0,0143 | 0,0125 |
- Solução
-
Para determinar a ordem da reação, precisamos traçar os dados usando três gráficos diferentes. Todos os três gráficos terão tempo em segundos como eixo x, mas o eixo y é o que será diferente. Um gráfico representará a concentração versus tempo, o segundo representará o logaritmo natural da concentração versus tempo e o outro representará o gráfico de 1/concentração versus tempos. Qualquer gráfico que resulte em uma linha, sabemos que essa deve ser a ordem da reação. Se obtivermos uma linha usando o primeiro gráfico, ela será de ordem zero, se for uma linha para o segundo gráfico, será de primeira ordem e, se for uma linha para o terceiro gráfico, será uma reação de segunda ordem. Agora vamos traçar os dados para determinar a ordem.



Podemos ver claramente que o terceiro gráfico, que traça 1/M em relação ao tempo, é uma linha reta, enquanto os outros dois são ligeiramente curvos. Portanto, podemos determinar que a taxa dessa reação é de segunda ordem. Isso também nos diz que as unidades da constante de taxa que deveriam ser M -2 s -1 para uma reação de segunda ordem.
Para determinar a constante de taxa, chamada k, precisamos simplesmente descobrir a inclinação do terceiro gráfico, pois essa é a ordem dessa reação. Para encontrar a inclinação da linha, pegamos dois pontos e subtraímos os valores y e os dividimos pela diferença dos valores x. É assim que se faz:
Use os pontos (5, 10.101) e (40, 80).
Agora use-os para obter a inclinação, também conhecida como constante de taxa: (80-10.101)/(40-5) = 1,997 = k
Portanto, a constante de taxa para essa reação de segunda ordem é 1,997 M -1 s -1.
Q12.4.6
Qual é a meia-vida da decomposição de primeira ordem do fósforo-32? \(\ce{(^{32}_{15}P⟶^{32}_{16}S + e- )}\)A constante de taxa para o decaimento é 4,85 × 10 −2 dia −1.
- Solução
-
Esta é uma reação de primeira ordem, então podemos usar nossa equação de meia-vida abaixo:
\[t_{1/2}=\frac{0.693}{k}\nonumber \]
A constante de taxa nos é dada em unidades por dia. Tudo o que precisamos fazer é conectá-lo à equação.
\[t_{1/2}=\frac{0.693}{4.85*10^{-2}}\nonumber \]
\[=14.3\; days\nonumber \]A12.4.6
14,3 d
Q12.4.7
Qual é a meia-vida da decomposição de primeira ordem do carbono-14? \(\ce{(^6_{14}C⟶^7_{14}N + e- )}\)A constante de taxa para o decaimento é 1,21 × 10 −4 ano −1.
- Solução
-
Para encontrar a meia-vida, precisamos usar a equação de meia-vida de primeira ordem. Todas as reações de meia-vida passam por reações de primeira ordem.
A equação de meia-vida de primeira ordem é\[t_{1/2}=ln2/k \nonumber \] com k sendo a taxa constante. A constante de taxa para o carbono-14 foi dada como\(1.21 × 10^{-4} year^{−1}\).
Conecte-o na equação. \[t_{1/2}=ln2/(1.21 × 10^{−4} year^{−1})\nonumber \]e resolva por\( t_{1/2}\).
Quando você calcula, a meia-vida do carbono-14 é 5,73*10 3
- Resposta
-
A meia-vida do carbono-14 é calculada em 5,73*10 3
Q12.4.8
Qual é a meia-vida para a decomposição de NOCl quando a concentração de NOCl é 0,15 M? A constante de taxa para essa reação de segunda ordem é 8,0 × 10 −8 L/mol/s.
- Solução
-
A meia-vida de uma reação, t 1/2, é a quantidade de tempo necessária para que a concentração de um reagente diminua pela metade em comparação com sua concentração inicial. Ao resolver a meia-vida de uma reação, devemos primeiro considerar a ordem da reação para determinar sua lei de taxas. Nesse caso, somos informados de que essa reação é de segunda ordem, então sabemos que a lei de taxas integradas é dada como:
\[\dfrac{1}{[A]} = kt + \dfrac{1}{[A]_0}\nonumber \]
Isolando o tempo, descobrimos que:
\[t_{1/2} = \dfrac{1}{k[A]_0}\nonumber \]
Agora é apenas uma questão de substituir as informações que recebemos para calcular\(t_{1/2}\), onde a constante de taxa,\({k}\), é igual a 8,0 × 10 −8 L/mol/s e a concentração inicial,\({[A]_0}\), é igual a 0,15 M:
\[t_{1/2} = \dfrac{1}{(8.0×10^{-8})(0.15)} = {8.33×10^7 seconds}\nonumber \]
- Resposta
-
8,33 × 10 7 s
Q12.4.9
Qual é a meia-vida para a decomposição de O 3 quando a concentração de O 3 é 2,35 × 10 −6 M? A taxa constante para essa reação de segunda ordem é 50,4 L/mol/h.
- Solução
-
Adicione textos aqui. Não exclua esse texto primeiro.
Como a reação é de segunda ordem, sua meia-vida é
\[t_{1/2}=\dfrac{1}{(50.4M^{-1}/h)[2.35×10^{-6}M]}\nonumber \]
Então, a meia-vida é de 8443 horas.
Q12.4.10
A reação do composto A para dar os compostos C e D foi considerada de segunda ordem em A. A constante de taxa para a reação foi determinada em 2,42 L/mol/s. Se a concentração inicial for 0,500 mol/L, qual é o valor de t 1/2?
- Solução
-
Conforme mencionado na pergunta, a reação do composto A resultará na formação dos compostos C e D. Esta reação foi considerada de segunda ordem em A. Portanto, devemos usar a equação de segunda ordem para meia-vida, que relaciona a taxa constante e as concentrações iniciais com a meia-vida:
\[t_{\frac{1}{2}}=\frac{1}{k[A]_{0}}\nonumber \]
Como recebemos k (constante de taxa) e concentração inicial de A, temos tudo o que é necessário para calcular a meia-vida de A.
\[k=0.5\frac{\frac{L}{mol}}{s}\nonumber \]
\[[A]_{0}=2.42\frac{mol}{L}\nonumber \]
Quando inserimos as informações fornecidas, observe que as unidades se cancelam em segundos.
\[t_{\frac{1}{2}}=\frac{1}{\frac{2.42Lmol^{-}}{s}[0.500\frac{mol}{L}]}=0.826 s\nonumber \]
- Resposta
-
0,826 s
Q12.4.11
A meia-vida de uma reação do composto A para dar os compostos D e E é de 8,50 minutos quando a concentração inicial de A é 0,150 mol/L. Quanto tempo levará para que a concentração caia para 0,0300 mol/L se a reação for (a) de primeira ordem em relação a A ou (b) segunda ordem em relação a A?
- Solução
-
Organize as variáveis fornecidas:
(meia-vida de A)\(t_{1/2}=8.50min\)
(concentração inicial de A)\([A]_{0}=0.150mol/L\)
(concentração alvo de A)\([A]=0.0300mol/L\)Encontre a constante de taxa k, usando as fórmulas de meia-vida para cada ordem respectiva. Depois de encontrar k, use a lei de taxa integrada respectiva a cada ordem e as concentrações inicial e alvo de A para encontrar o tempo necessário para a concentração cair.
(a) primeira ordem em relação a A
(meia-vida)\(t_{1/2}=\frac{ln(2)}{k}=\frac{0.693}{k}\)
(rearranjado para k)\(k=\frac{0.693}{t_{1/2}}\)
(conecte t 1/2 = 8,50 min)\(k=\frac{0.693}{8.50min}=0.0815min^{-1}\)(lei de taxa integrada)\(ln[A]=-kt+ln[A]_{0}\)
(reorganizada para t)\(ln(\frac{[A]}{[A]_{0}})=-kt\)
\(-ln(\frac{[A]}{[A]_{0}})=kt\)
\(ln(\frac{[A]}{[A]_{0}})^{-1}=kt\)
\(ln(\frac{[A]_{0}}{[A]})=kt\)
\(t=\frac{ln(\frac{[A]_{0}}{[A]})}{k}\)
(insira variáveis)\(t=\frac{ln(\frac{0.150mol/L}{0.0300mol/L})}{0.0815min^{-1}}=\frac{ln(5.00)}{0.0815min^{-1}}=19.7min\)(b) segunda ordem em relação a A
(meia-vida)\(t_{1/2}=\frac{1}{k[A]_{0}}\)
(rearranjado para k)\(k=\frac{1}{t_{1/2}[A]_{0}}\)
(insira variáveis)\(k=\frac{1}{(8.50min)(0.150mol/L)}=\frac{1}{1.275min\cdot mol/L}=0.784L/mol\cdot min\)(lei de taxa integrada)\(\frac{1}{[A]}=kt+\frac{1}{[A]_{0}}\)
(reorganizada para t)\(\frac{1}{[A]}-\frac{1}{[A]_{0}}=kt\)
\(t=\frac{1}{k}(\frac{1}{[A]}-\frac{1}{[A]_{0}})\)
(insira variáveis)\(t=\frac{1}{0.784L/mol\cdot min}(\frac{1}{0.0300mol/L}-\frac{1}{0.150mol/L})=\frac{1}{0.784L/mol\cdot min}(\frac{80}{3}L/mol)=34.0min\)
- Resposta
-
a) 19,7 min
b) 34,0 min
Q12.4.12
Algumas bactérias são resistentes ao antibiótico penicilina porque produzem penicilinase, uma enzima com peso molecular de 3 × 10 4 g/mol que converte a penicilina em moléculas inativas. Embora a cinética das reações catalisadas por enzimas possa ser complexa, em baixas concentrações essa reação pode ser descrita por uma equação de taxa que é de primeira ordem no catalisador (penicilinase) e que também envolve a concentração de penicilina. A partir dos seguintes dados: 1,0 L de uma solução contendo 0,15 µg (0,15 × 10 −6 g) de penicilinase, determine a ordem da reação em relação à penicilina e o valor da constante de taxa.
| [Penicilina] (M) | Taxa (mol/L/min) |
|---|---|
| 2,0 × 10 −6 | 1,0 × 10 −10 |
| 3,0 × 10 −6 | 1,5 × 10 −10 |
| 4,0 × 10 −6 | 2,0 × 10 −10 |
- Solução
-
O primeiro passo é resolver a ordem ou a reação. Isso pode ser feito configurando duas expressões que igualam a taxa à taxa constante vezes a concentração molar de penicilina elevada à potência de sua ordem. Depois de configurar as duas expressões, podemos dividi-las para cancelar k (constante de taxa) e usar um logaritmo básico para resolver o expoente, que é a ordem. Vai ficar assim.
taxa (mol/L/min) =k [M] x
(1,0 x 10 -10) =k [2,0 x 10 -6] x
(1,5 x 10 -10) =k [3,0 x 10 -6] x
A divisão das duas equações resulta na expressão:
(2/3) = (2/3) x
*Uma equação de razão única também pode ser configurada para resolver a ordem de reação:
*\[\frac{rate_{1}}{rate_{2}}=\frac{k[Penicillin]_{1}^{x}}{k[Penicillin]_{2}^{x}}\nonumber \]
*Em seguida, resolvemos para x de forma semelhante.
*\[\frac{1.0x10^{-10}}{1.5x10^{-10}}=\frac{[2.0x10^{-6}]^{x}}{[3.0x10^{-6}]^{x}}\nonumber \]
Agora podemos usar o logaritmo natural para resolver x, ou simplesmente e intuitivamente ver que, para que a equação funcione, x deve ser igual a um. Assim, a reação é de primeira ordem.
Agora que temos a ordem da reação, podemos prosseguir com a solução para o valor da constante de taxa. Substituindo x=1 em nossa primeira equação produz a expressão:(1 x 10 -10) =k [2,0 x 10 -6] 1
k= (1 x 10 -10)/(2 x 10 -6)
k= (5 x 10 -5) min -1
Temos uma unidade de min -1 porque dividimos (mol/L/min) pela molaridade, que está em (mol/L), produzindo uma unidade de min -1.
Recebemos duas informações importantes para resolver o problema. Afirma-se que a enzima tem um peso molecular de 3 × 10 4 g/mol e que temos uma solução de um litro que contém (0,15 x 10 -6 g) de penicilinase. Dividindo a quantidade de gramas pelo peso molecular, obtém-se 5 x 10 -12 moles.
(0,15 x 10 -6) g/(3 x 10 4) g/mol = (5 x 10 -12) mol
Agora que temos a quantidade de moles, podemos dividir nossa constante de taxa por esse valor.
(5 x 10 -5) min -1/(5 x 10 -12) mol = (1 x 10 7) mol -1 min -1
Resposta
-
A reação é de primeira ordem com k = 1,0 × 10 7 mol −1 min −1
Q12.4.13
Tanto o tecnécio-99 quanto o tálio-201 são usados para obter imagens do músculo cardíaco em pacientes com suspeita de problemas cardíacos. As meias-vidas são de 6 h e 73 h, respectivamente. Qual porcentagem da radioatividade permaneceria para cada um dos isótopos após 2 dias (48 h)?
- Solução
-
Esse problema está nos perguntando a porcentagem de radioatividade restante após um certo tempo para ambos os isótopos após 48 horas. Precisamos identificar uma equação que nos ajude a resolver isso e podemos determinar se podemos determinar essas informações usando a equação de primeira ordem.
Essa equação Ln (N/N o) = -kt diz que o log natural da fração restante é igual à taxa constante vezes o tempo. Para determinar a constante de taxa, também podemos calcular 0,693 ao longo da meia-vida dada nas informações.
Para o Tecnécio-99, podemos determinar a constante de taxa conectando-se à segunda equação: .693/6 horas = .1155 h -1
Agora que temos a constante de taxa, podemos inserir: Ln (N/N o) =- (.1155h -1) (48h) então Ln (N/N o) =-5,544 e se tomarmos o inverso do log natural, obtemos (N/N o) =3,9x10 -3 e se multiplicarmos isso por 100, obtemos 0,39% restantes.
Podemos fazer esse mesmo processo para Thallium-201 e plugin: .693/73 hrs= .009493151 h -1 e quando inserimos isso na equação de primeira ordem, obtemos:
Ln (N/N o) =- (.009493h -1) (48h) então Ln (N/N o) =-.45567248 e quando tomamos o inverso do log natural, obtemos (N/N o) =.6340 e quando multiplicados por 100, obtemos 63,40% restantes, o que faz sentido, já que sua meia-vida é de 73 horas e apenas 48 horas passaram, metade da quantidade ainda não foi consumida.
- Resposta
-
Tecnécio-99:0,39%
Tálio-201:63,40%
Q12.4.14
Existem duas moléculas com a fórmula C 3 H 6. Propeno\(\ce{CH_3CH=CH_2}\),, é o monômero do polímero polipropileno, usado para tapetes internos e externos. O ciclopropano é usado como anestésico:

Quando aquecido a 499° C, o ciclopropano se reorganiza (isomeriza) e forma propeno com uma taxa constante de 5,95 × 10 −4 s −1. Qual é a meia-vida dessa reação? Qual fração do ciclopropano permanece após 0,75 h a 499 °C?
- Solução
-
Use a equação,\[ t{_1}{_/}{_2} = \frac{ln2} k\nonumber \] pois essa é uma reação de primeira ordem. Você pode dizer que esta é uma reação de primeira ordem devido às unidades de medida da constante de taxa, que é s -1. Diferentes ordens de reações levam a diferentes constantes de taxa, e uma constante de taxa de s -1 sempre será de primeira ordem.
Conecte-se à equação e você terá meia-vida = 1164,95 segundos. Para converter isso em horas, dividiríamos esse número por 3600 segundos/hora, para obter 0,324 horas.
Use a lei integrada de taxas de primeiro pedido\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]. Nesta equação, [A] 0 representa a quantidade inicial de composto presente no tempo 0, enquanto [A] representa a quantidade de composto que resta após a ocorrência da reação. Portanto, a fração\[\frac{[A]}{[A]_0}\nonumber \] é igual à fração de ciclopropano que permanece após um certo período de tempo, neste caso, 0,75 horas.
Substitua x pela fração de\[\frac{[A]}{[A]_0}\nonumber \] na lei da taxa integrada:\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]\[ln(x) = -5.95x10^{-4}(0.75)\nonumber \]\[x=e^{(-0.000595)(0.75)}\nonumber \] = 0,20058 = 20%.
Portanto, a meia-vida é de 0,324 horas e 20% do ciclopropano permanecerá, pois 80% terão formado propeno.
- Resposta
-
0,324 horas.; 20% permanecem
Q12.4.16
O flúor-18 é um isótopo radioativo que decai por emissão de pósitrons para formar oxigênio-18 com meia-vida de 109,7 min. (Um pósitron é uma partícula com a massa de um elétron e uma única unidade de carga positiva; a equação nuclear é\(\ce{^{18}_9F ⟶ _8^{18}O + ^0_{1}e^+}\).) Os médicos usam 18 F para estudar o cérebro injetando uma quantidade de glicose substituída por flúor no sangue de um paciente. A glicose se acumula nas regiões onde o cérebro está ativo e precisa ser nutrida.
- Qual é a taxa constante para a decomposição do flúor-18?
- Se uma amostra de glicose contendo flúor-18 radioativo for injetada no sangue, qual porcentagem da radioatividade permanecerá após 5,59 h?
- Quanto tempo leva Fe para 99,99% do 18 F decair?
- Solução
-
a) O decaimento nuclear de um isótopo de um elemento é representado pela equação de primeira ordem:
ln (N/N0) = −kt
Onde t é tempo, N0 é a quantidade inicial da substância, N é a quantidade da substância após o tempo t e k é a taxa constante. Podemos reorganizar a equação e isolar k para que possamos resolver a constante de taxa:
k = [-ln (N/N0)]/t
Sabemos que o flúor-18 tem meia-vida de 109,7 minutos. Como temos a meia-vida, podemos escolher um valor arbitrário para N 0 e usar metade desse valor para N. Nesse caso, escolhemos 100 para N 0 e 50 para N. Agora podemos inserir esses valores na equação acima e resolver para k.
k = [-ln (50/100)]/109,7
k = 0,6931/109,7 = 0,006319 min -1
A constante de taxa para essa reação é 0,006319 min -1.
b) Para esse problema, podemos usar a mesma equação da parte a:
ln (N/N0) = −kt
No entanto, desta vez, recebemos a quantidade de tempo decorrido em vez da meia-vida, e somos solicitados a determinar a porcentagem de radioatividade de flúor-18 restante após esse período. Nesse problema, devemos inserir valores para N0, k (determinado a partir da parte a) e t.
Mas primeiro, como recebemos o tempo decorrido em horas, devemos convertê-lo em minutos:
5,59 horas x (60 minutos/1 hora) = 335,4 minutos
Isso nos dá o valor de t. Também temos valores para k (0,006319 min -1) e N 0 (novamente, um número arbitrário). Agora podemos inserir valores na equação original, fornecendo:
ln (N/100) = − (0,006319) (335,4)
Resolvemos essa equação tomando a exponencial de ambos os lados:
e ln (N/100) = e − (0,006319) (335,4)
onde e ln é igual a 1 e agora podemos resolver para N:
N/100 = e − (0,006319) (335,4)
N = [e − (0,006319) (335,4)] x 100 = 12,0
Como 100 foi usado como a quantidade inicial e 12,0 foi determinado como a quantidade restante, 12,0 pode ser usado como a porcentagem da quantidade restante de radioatividade do flúor-18. Assim, a porcentagem de radioatividade de flúor-18 restante após 5,59 horas é de 12,0%.
c) Essa parte da questão é muito parecida com as duas partes anteriores, mas desta vez recebemos a quantidade inicial de radioatividade, a quantidade final de radioatividade e somos solicitados a determinar quanto tempo demorou para que essa quantidade de radioatividade decaísse. Somos capazes de usar a mesma equação:
ln (N/N0) = −kt
No entanto, agora recebemos N e N 0 e já determinamos k de antes. Somos informados de que 99,99% da radioatividade diminuiu, então podemos usar 100 e 0,01 para N 0 e N, respectivamente. Nós inserimos esses valores na equação, resolvemos para t e obtemos
ln (0,01/1000) = −0,006319t
-9,21 = −0,006319t
t = 1458 minutos
Portanto, são necessários 1458 minutos para que 99,99% da radioatividade decaia.
- Resposta
-
a) 0,006319 min -1
b) 12,0%
c) 1458 minutos
Q12.4.17
Suponha que a meia-vida dos esteróides tomados por um atleta seja de 42 dias. Supondo que os esteróides se biodegradem por um processo\(\dfrac{1}{64}\) de primeira ordem, quanto tempo a dose inicial levaria para permanecer no corpo do atleta?
- Solução
-
252 dias
para reação de primeira ordem: t 1/2 = 0,693/k
k = 0,693/42
k = 0,0165
para reação de primeira ordem: [A] = [A] 0 e -kt
1/64 inicial significa que: [A] = 1/64 [A] 0
portanto: 1/64 [A] 0 = [A] 0 e -0,0165t
t = 252 dias
Q12.4.18
Recentemente, o esqueleto do rei Ricardo III foi encontrado embaixo de um estacionamento na Inglaterra. Se as amostras de tecido do esqueleto contêm cerca de 93,79% do carbono-14 esperado em tecidos vivos, em que ano o rei Ricardo III morreu? A meia-vida do carbono-14 é de 5 a 30 anos.
- Solução
-
Para descobrir em que ano o rei Ricardo III morreu, defina [A]/[A 0] (a porcentagem de carbono-14 ainda contida) igual a 0,5 vez (t) /meia-vida (t 1/2) ou use a equação N (t) = N 0 e -rt.
Usando a primeira equação:
\(A/A_{0}\)=\(0.5^{t/t_{1/2}}\) insira os números fornecidos\(.9379 = 0.5^{t/5730}\) e resolva para t.
\(ln.9379\)=\((t/5730)(ln0.5)\) (usando a regra dos registros)
\(-.0641\)=\((t/5730)(-.693)\)
\(-367.36\)=\(-.693t\)
\(t = 530.1 years\)
O uso\(N(t) = N_{0}e^{-rt}\) desse problema é resolvido da seguinte forma:
\(1/2 = e^{-5730r}\)
\(r = 0.000121\)
Agora que sabemos o que é r, podemos usar esse valor em nossa fórmula original e resolver para t, a quantidade de anos que passaram.
Desta vez, usamos 93,78, a porcentagem do carbono-14 permanecendo como N (t) e 100 como o original, N 0.
\(93.78 = 100e^{-0.000121t}\)
\(t = 530.7\)anos
Outra forma de fazer isso é usando essas duas equações:
λ =\(\dfrac{0.693}{t_{1/2}}\) e\(\dfrac{n_{t}}{n_{0}}\) = -λt
\(n_{t}\)= concentração no tempo t (93,79)
\(n_{0}\)= concentração inicial (100)
Primeiro, resolva a lambda ou a constante de decaimento conectando a meia-vida.
Em seguida, insira lambda e os outros números na segunda equação e resolva para t-, que também deve ser igual a 530,1 anos.
Se quisermos descobrir em que ano o rei Ricardo III morreu, pegamos o ano atual, 2017, e subtraímos 530 anos. Fazendo isso, descobrimos que o rei Ricardo III morreu no ano de 1487.
- Resposta
-
Rei Ricardo III morreu no ano 1487.
Q12.4.19
A nitroglicerina é um explosivo extremamente sensível. Em uma série de experimentos cuidadosamente controlados, amostras do explosivo foram aquecidas a 160 °C e sua decomposição de primeira ordem estudada. Determine as constantes de taxa média para cada experimento usando os seguintes dados:
| Inicial [C 3 H 5 N 3 O 9] (M) | 4,88 | 3,52 | 2,29 | 1,81 | 5.33 | 4,05 | 2,95 | 1,72 |
|---|---|---|---|---|---|---|---|---|
| t (s) | 300 | 300 | 300 | 300 | 180 | 180 | 180 | 180 |
| % Decomposto | 52,0 | 52,9 | 53.2 | 53,9 | 34,6 | 35,9 | 36,0 | 35,4 |
- Solução
-
Primeiro, precisamos entender o que a pergunta está pedindo: a constante da taxa média. A constante de taxa média é a variável “k” ao discutir a cinética e pode ser definida como a constante de proporcionalidade na equação que expressa a relação entre a taxa de uma reação química e as concentrações das substâncias que reagem. Sabendo que precisamos encontrar K nessa reação de primeira ordem, podemos procurar fórmulas que incluem “k”\([A]_o and [A]_t\), concentrações iniciais e finais e tempo de meia-vida “t”. Como essa é uma reação de primeira ordem, podemos examinar as equações de primeira ordem e, fazendo isso, encontrar uma que inclua as variáveis dadas na pergunta:\[\ln[A]_t=-kt+\ln[A]_o\nonumber \]
Para a primeira reação, temos uma concentração inicial de 4,88 M e uma porcentagem decomposta. Para encontrar a concentração final, devemos multiplicar a concentração inicial pela porcentagem decomposta para saber o quanto está decomposto e subtraí-la do original para descobrir quanto resta: 4,88M x 0,52= 2,54 M e 4,88M-2,54M = 2,34M
Agora, temos as variáveis de que precisamos e as inserimos na equação acima:
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.34M]=-k(300s)+\ln[4.88M]\)
k=\({-(\ln[2.34M]-\ln[4.88M])}\over 300\)
\(k=2.45x10^{-3}\)
Como ele solicita a constante de taxa de cada experimento, agora precisamos fazer o mesmo procedimento para cada conjunto de dados para encontrar a constante de taxa:
Segundo experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.66M]=-k(300s)+\ln[3.52M]\)
k=\({-(\ln[1.66M]-\ln[3.52M])}\over 300\)
\(k=2.51x10^{-3}\)
Terceiro experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.07M]=-k(300s)+\ln[2.29M]\)
k=\({-(\ln[1.07M]-\ln[2.29M])}\over 300\)
\(k=2.54x10^{-3}\)
Quarto experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[0.834M]=-k(300s)+\ln[1.81M]\)
k=\({-(\ln[0.834M]-\ln[1.81M])}\over 300\)
\(k=2.58x10^{-3}\)
Quinto experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[3.49M]=-k(180s)+\ln[5.33M]\)
k=\({-(\ln[3.49M]-\ln[5.33M])}\over 180\)
\(k=2.35x10^{-3}\)
Sexta experiência
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.60M]=-k(180s)+\ln[4.05M]\)
k=\({-(\ln[2.60M]-\ln[4.05M])}\over 180\)
\(k=2.46x10^{-3}\)
Sétima experiência
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.89M]=-k(180s)+\ln[2.95M]\)
k=\({-(\ln[1.89M]-\ln[2.95M])}\over 180\)
\(k=2.47x10^{-3}\)
Oitavo experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.11M]=-k(180s)+\ln[1.72M]\)
k=\({-(\ln[1.11M]-\ln[1.72M])}\over 180\)
\(k=2.43x10^{-3}\)
- Resposta
-
[A] 0 (M) k × 10 (3 s −1) 4,88 2,45 3,52 2,51 2,29 2,54 1,81 2,58 5.33 2,35 4,05 2,44 2,95 2,47 1,72 2,43
Q12.4.20
Nos últimos 10 anos, o hidrocarboneto insaturado 1,3-butadieno\(\ce{(CH2=CH–CH=CH2)}\) ficou em 38º lugar entre os 50 principais produtos químicos industriais. É usado principalmente para a fabricação de borracha sintética. Um isômero também existe como ciclobuteno:

A isomerização do ciclobuteno em butadieno é de primeira ordem e a constante da taxa foi medida como 2,0 × 10 −4 s −1 a 150 °C em um frasco de 0,53-L. Determine a pressão parcial do ciclobuteno e sua concentração após 30,0 minutos se uma reação de isomerização for realizada a 150 °C com uma pressão inicial de 55 torr.
- Solução
-
Como essa é uma reação de primeira ordem, a lei de taxa integrada é: Pressão\([A_{t}]=[A_{0}]e^{-kt}\)
parcial: Use a lei de taxa integrada para encontrar a pressão parcial em 30 minutos:Use\(A_0\) = 55 torr, t = 30 min e k =\(2.0 * 10^{-4}s^{-1}\) para resolver a equação da lei de taxa integrada:
\([A_{30}]=(55 torr)*e^{-(2.0x10^{-4}\frac{1}{sec})(30min\cdot\frac{60sec}{1 min})}\)
Resolva essa equação para obter:
\([A_{30}]=(55 torr)*e^{-0.36}\)
\(A_{30}]\)= 38,37 torr.
Concentração inicial: Encontre a concentração inicial usando a lei do gás ideal.
A lei do gás ideal é dada por\(PV = nRT → n = \frac{PV}{RT}\). Use essa forma da lei do gás para resolver a concentração inicial n.
Use V = 0,53L, R = 0,08206\(\frac{L*atm}{mol*L}\), T = 423,15 K e P\(\frac{1 atm}{760}\) = 0,07237 atm.
Resolva a equação do gás ideal usando esses valores:
\(n=\frac{(55torr)(0.53L)}{(0.08206\frac{L*atm}{mol*K})(423.15K)} = 0.00110\)toupeiras de ciclobuteno.
Agora, encontre a concentração inicial de ciclobuteno\(A_0\) usando a equação\([A_0] = \frac{n}{V}\):
\(A_0 = \frac{n}{V} = \frac{0.00110 moles}{0.53 L} = 0.00208 M\)
Concentração em 30 minutos: Encontre a concentração de ciclobuteno em 30 minutos usando a lei de taxa integrada fornecida acima, usando o tempo t = 30 minutos ou 1800 segundos.
\([A_{30}]=(0.00208M)e^{-0.36}= 0.00145M\)
Então, aos 30 minutos, a concentração de ciclobuteno é 0,00145 M e a pressão parcial é 38,37 torr.
- Resposta
-
Pressão parcial: 38,37 torr.
Concentração: 0,00145 M
12.5: Teoria da colisão
Q12.5.1
As reações químicas ocorrem quando os reagentes colidem. Quais são os dois fatores que podem impedir que uma colisão produza uma reação química?
- Solução
-
Os dois fatores que podem impedir que uma colisão produza uma reação química são:
1. Energia cinética da molécula
Para que as reações químicas ocorram, as moléculas precisam de velocidade suficiente para superar a energia de ativação mínima necessária para romper as ligações antigas e formar novas ligações com outras moléculas. Em temperaturas mais altas, as moléculas possuem a quantidade mínima de energia cinética necessária, o que garante que as colisões sejam energéticas o suficiente para levar a uma reação.
2. A orientação das moléculas durante a colisão
Duas moléculas precisam colidir na orientação correta para que a reação ocorra. As moléculas precisam se orientar adequadamente para que outra molécula colida no estado de ativação correto.
Q12.5.2
Quando cada colisão entre reagentes leva a uma reação, o que determina a taxa na qual a reação ocorre?
- Solução
-
É necessário que haja contato entre os reagentes para que uma reação ocorra. Quanto mais os reagentes colidem, mais frequentemente as reações podem ocorrer. Os fatores que determinam as taxas de reação incluem concentração de reagentes, temperatura, estados físicos dos reagentes, área de superfície e uso de um catalisador. A taxa de reação geralmente aumenta à medida que a concentração de um reagente aumenta. O aumento da temperatura aumenta a energia cinética média das moléculas, fazendo com que elas colidam com mais frequência, o que aumenta a taxa de reação. Quando dois reagentes estão na mesma fase de fluido, suas partículas colidem com mais frequência, o que aumenta a taxa de reação. Se a área da superfície de um reagente for aumentada, mais partículas serão expostas ao outro reagente, portanto, mais colisões ocorrem e a taxa de reação aumenta. Um catalisador participa de uma reação química e aumenta a taxa de reação sem se alterar.
Q12.5.3
Qual é a energia de ativação de uma reação e como essa energia está relacionada ao complexo ativado da reação?
- Solução
-

A energia de ativação é a barreira de energia que deve ser superada para que uma reação ocorra. Para colocar as moléculas em um estado que lhes permita quebrar e formar ligações, as moléculas devem ser contorcidas (deformadas ou dobradas) em um estado instável chamado estado de transição. O estado de transição é um estado de alta energia, e uma certa quantidade de energia — a energia de ativação — deve ser adicionada para que a molécula o alcance. Como o estado de transição é instável, as moléculas reagentes não permanecem lá por muito tempo, mas passam rapidamente para a próxima etapa da reação química. O complexo ativado é a energia mais alta do estado de transição da reação.
Q12.5.5
Descreva como métodos gráficos podem ser usados para determinar a energia de ativação de uma reação a partir de uma série de dados que inclui a taxa de reação em temperaturas variáveis.
- Solução
-
Este método é baseado na equação de Arrhenius, que pode ser usada para mostrar o efeito de uma mudança de temperatura na constante de taxa e, portanto, na taxa de reação.
A constante de taxa é diferente da taxa de reação, pois a taxa de reação é a medida de quão rápida ou lenta uma reação química ocorre, enquanto uma constante de taxa é uma constante que mostra a relação entre a taxa de reação e as concentrações dos reagentes ou produtos.
Por exemplo, para a reação\(A + B \rightarrow C\), the rate law would be:
\(rate = k[A]^a[B]^b\)
k = taxa constante
[A] = concentração do reagente A
a = ordem de reação em relação a A
[B] = concentração do reagente B
b = ordem de reação em relação a B
No entanto, a constante de taxa permanece constante somente se você estiver alterando a concentração dos reagentes. Se você alterar a temperatura ou o catalisador da reação, a constante da taxa mudará e isso é demonstrado pela equação de Arrhenius:
\(k = Ae^\frac{-E_a}{RT}\)
\(ln \left(\frac{k_1}{k_2}\right) = \left(\frac{-E_a}{R}\right)\left(\frac{1}{T_1} - \frac{1}{T_2}\right)\)
k = taxa constante
A = fator de frequência
\(E_a\) = activation energy
e = função exponencial,\(e^x\)
R = constante do gás
T = temperatura (K)

Em outras palavras, a energia de ativação de uma reação,\(E_a\), from a series of data that includes the rate of reaction, k, at varying temperatures can be determined by graphing it on a plot of \(\ln k\) versus \(\frac{1}{T}\). You can then use the slope of the graph you have plotted to solve for \(E_a\) by setting the slope equal to \(\frac{-E_a}{R}\).
Q12.5.6
How does an increase in temperature affect rate of reaction? Explain this effect in terms of the collision theory of the reaction rate.
S12.5.6
Collision theory states that the rates of chemical reactions depend on the fraction of molecules with the correct orientation, fraction of collisions with required energy, and the collision frequency. Because the fraction of collisions with required energy is a function of temperature, as temperature increases, the fraction of collisions with required energy also increases. The kinetic energy of reactants also increases with temperature which means molecules will collide more often increasing collisions frequency. With increased fraction of collisions with required energy and collisions frequency, the rate of chemical reaction increases. We see mathematically, from the Arrhenius equation, that temperature and the rate constant are related.
\[k=Ae^{\frac {E_a}{RT}}\]
where k is the rate constant, A is a specific constant, R is 8.3145 J/K, Ea is the reaction-specific activation energy in J, and T is temperature in K. We see from the equation that k is very sensitive to changes in the temperature.
Q12.5.7
The rate of a certain reaction doubles for every 10 °C rise in temperature.
- How much faster does the reaction proceed at 45 °C than at 25 °C?
- How much faster does the reaction proceed at 95 °C than at 25 °C?
- Solution
-
By finding the difference in temperature, 45 °C - 25 °C, we get 20 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the rate of the reaction experienced a 20 °C increase in temperature, we see that the reaction rate doubled twice (22 = 4). As a result, the reaction proceeds four times faster.
Following the same process as in part a, we get the difference in temperature to be 70 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the system experienced a 70 °C change, we see that the reaction doubled seven times (27 = 128). We can see the reaction proceeds 128 times faster.
(a) 4-times faster (b) 128-times faster
Q12.5.8
In an experiment, a sample of NaClO3 was 90% decomposed in 48 min. Approximately how long would this decomposition have taken if the sample had been heated 20 °C higher?
S12.5.8
First off, it is important to recognize that this decomposition reaction is a first-order reaction, which can be written as follows: \(\mathrm2NaClO_3\to2NaCl + 3O_2\)
Understanding this, it is important to be able to then be able to recognize which equation would be most useful given the initial conditions presented by the question. Since we are dealing with time, percentage of material left, and temperature, the only viable equation that could relate all of this would be the Arrhenius Equation, which is written as follows: \(\mathrm \ln(\frac{k_2}{k_1}) = \frac {Ea}{R}({\frac1{t_1}}-{\frac{1}{t_{2}}})\)
However, this problem does not give us enough information such as what the activation energy is or the initial temperature in order to mathematically solve this problem. Additionally, the problem tells us to approximate how long the decomposition would take, which means we are asked to answer this question conceptually based on our knowledge of thermodynamics and reaction rates. As a general rule of thumb, we know that for every 10˚C rise in temperature the rate of reaction doubles. Since the question tells us that there is a 20˚C rise in temperature we can deduce that the reaction rate doubles twice, as per the general rule mentioned before. This means the overall reaction rate for this decomposition would quadruple, or would be 4 times faster than the reaction rate at the initial temperature.
We can gut check this answer by recalling how an increase in the average kinetic energy (temperature) decreases the time it takes for the reaction to take place and increase the reaction rate. Thus, if we increase the temperature we should have a faster reaction rate.
Q12.5.9
The rate constant at 325 °C for the decomposition reaction \(\ce{C4H8⟶2C2H4}\) is 6.1 × 10−8 s−1, and the activation energy is 261 kJ per mole of C4H8. Determine the frequency factor for the reaction.
- Solution
-
S12.5.9
Using the Arrhenius equation allows me to find the frequency factor, A.
k=Ae-Ea/RT
k, Ea, R, and T are all known values. k, Ea, and T are given in the problem as 6.1x10-8, 261 kJ, and 598 K, respectively.
So, plugging them into the equation gives:
6.1x10-8 s-1=Ae(-261000 J)/(8.3145 J/mol)(598 K)
Take e(-261000 J)/(8.3145 J/mol)(598) and get 1.59 x 10-23. Divide k, 6.1 x 10-8, by 1.59 x 10-23 and get A=3.9 x 1015s-1
-
A12.5.9
\(\mathrm{3.9×10^{15}\:s^{−1}}\)
Q12.5.10
The rate constant for the decomposition of acetaldehyde (CH3CHO), to methane (CH4), and carbon monoxide (CO), in the gas phase is 1.1 × 10−2 L/mol/s at 703 K and 4.95 L/mol/s at 865 K. Determine the activation energy for this decomposition.
S12.5.10
The equation for relating the rate constant and activation energy of a reaction is the Arrhenius equation:
\[k = Ae^ {-\frac{E_a}{RT}}\]
When given two rate constants at two different temperatures but for the same reaction, the Arrhenius equation can be rewritten as:
\[ln (\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2})\]
In this problem, all the variables are given except for the Ea (activation energy).
k1 = 1.1 × 10−2 L/mol/s
T1 = 703 K
k2 = 4.95 L/mol/s
T2 = 865 K
R = 8.314 J/(mol K) (Ideal Gas Constant)
Now plug in all these values into the equation, and solve for Ea.
\[ln (\frac{4.95\frac{L}{mol×s}}{1.1 × 10^{-2}\frac{L}{mol×s}}) = \frac{E_a}{8.314 × 10^{-3}\frac{kJ}{mol×K}} (\frac{1}{703} - \frac{1}{865})\]
Ea = 190 kJ (2 sig figs)
Q12.5.11
An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorder. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?
- Solution
-
43.0 kJ/mol
Q12.5.12
In terms of collision theory, to which of the following is the rate of a chemical reaction proportional?
- the change in free energy per second
- the change in temperature per second
- the number of collisions per second
- the number of product molecules
Q12.5.13
Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H2, and iodine, I2. The value of the rate constant, k, for the reaction was measured at several different temperatures and the data are shown here:
| Temperature (K) | k (M−1 s−1) |
|---|---|
| 555 | 6.23 × 10−7 |
| 575 | 2.42 × 10−6 |
| 645 | 1.44 × 10−4 |
| 700 | 2.01 × 10−3 |
What is the value of the activation energy (in kJ/mol) for this reaction?
- Solution
-
177 kJ/mol
Q12.5.14
The element Co exists in two oxidation states, Co(II) and Co(III), and the ions form many complexes. The rate at which one of the complexes of Co(III) was reduced by Fe(II) in water was measured. Determine the activation energy of the reaction from the following data:
| T (K) | k (s−1) |
|---|---|
| 293 | 0.054 |
| 298 | 0.100 |
Q12.5.15
The hydrolysis of the sugar sucrose to the sugars glucose and fructose,
\[\ce{C12H22O11 + H2O ⟶ C6H12O6 + C6H12O6}\nonumber \]
follows a first-order rate equation for the disappearance of sucrose: Rate = k[C12H22O11] (The products of the reaction, glucose and fructose, have the same molecular formulas but differ in the arrangement of the atoms in their molecules.)
- In neutral solution, k = 2.1 × 10−11 s−1 at 27 °C and 8.5 × 10−11 s−1 at 37 °C. Determine the activation energy, the frequency factor, and the rate constant for this equation at 47 °C (assuming the kinetics remain consistent with the Arrhenius equation at this temperature).
- When a solution of sucrose with an initial concentration of 0.150 M reaches equilibrium, the concentration of sucrose is 1.65 × 10−7 M. How long will it take the solution to reach equilibrium at 27 °C in the absence of a catalyst? Because the concentration of sucrose at equilibrium is so low, assume that the reaction is irreversible.
- Why does assuming that the reaction is irreversible simplify the calculation in part (b)?
- Solution
-
Ea = 108 kJ
A = 2.0 × 108 s−1
k = 3.2 × 10−10 s−1
(b) 1.81 × 108 h or 7.6 × 106 day. (c) Assuming that the reaction is irreversible simplifies the calculation because we do not have to account for any reactant that, having been converted to product, returns to the original state.
Q12.5.16
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “straight shot” default option, try launching the A atom with varying amounts of energy. What changes when the Total Energy line at launch is below the transition state of the Potential Energy line? Why? What happens when it is above the transition state? Why?
Q12.5.17
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “angled shot” option, try launching the A atom with varying angles, but with more Total energy than the transition state. What happens when the A atom hits the BC molecule from different directions? Why?
- Solution
-
The A atom has enough energy to react with BC; however, the different angles at which it bounces off of BC without reacting indicate that the orientation of the molecule is an important part of the reaction kinetics and determines whether a reaction will occur.
12.6: Reaction Mechanisms
Q12.6.1
Why are elementary reactions involving three or more reactants very uncommon?
Q12.6.2
In general, can we predict the effect of doubling the concentration of A on the rate of the overall reaction \(A+B⟶C\) ? Can we predict the effect if the reaction is known to be an elementary reaction?
- Solution
-
Add texts here. Do not delete this text first.
No. In general, for the overall reaction, we cannot predict the effect of changing the concentration without knowing the rate equation. Yes. If the reaction is an elementary reaction, then doubling the concentration of A doubles the rate.
Q12.6.3
Phosgene, COCl2, one of the poison gases used during World War I, is formed from chlorine and carbon monoxide. The mechanism is thought to proceed by:
| step 1: | Cl + CO → COCl |
| step 2: | COCl + Cl2→ COCl2 + Cl |
- Write the overall reaction equation.
- Identify any reaction intermediates.
- Identify any intermediates.
Q12.6.4
Define these terms:
- unimolecular reaction
- bimolecular reaction
- elementary reaction
- overall reaction
Q12.6.5
What is the rate equation for the elementary termolecular reaction \(A+2B⟶\ce{products}\)? For \(3A⟶\ce{products}\)?
- Solution
-
Add texts here. Do not delete this text first.
We are given that both of these reactions are elementary termolecular. The molecularity of a reaction refers to the number of reactant particles that react together with the proper and energy and orientation. Termolecular reactions have three atoms to collide simultaneously. As it is termolecular, and there are no additional reactants aside from the three given in each reaction, there are no intermediate reactions. The rate law for elementary reactions is determined by the stoichiometry of the reaction without needed experimental data.
The basic rate form for the elementary step is what follows:
\(rate= {k} \cdot {reactant \ 1}^{i} \cdot {reactant \ 2}^{ii} \cdot ... \) Where i and ii are the stochiometric coefficient from reactant 1 and 2 respectively.
For: \(3A \rightarrow products \)
\({k} \cdot {A}^3 = rate\)
For: \(A + 2B \rightarrow products \)
\({k} \cdot {[A]} \cdot {[B]}^2 = rate\)
Note that the order of these reactions are both three.
- Answer
-
Add texts here. Do not delete this text first.
Rate = k[A][B]2; Rate = k[A]3
Q12.6.6
Given the following reactions and the corresponding rate laws, in which of the reactions might the elementary reaction and the overall reaction be the same?
(a) \(\ce{Cl2 + CO ⟶ Cl2CO}\)
\(\ce{rate}=k\ce{[Cl2]^{3/2}[CO]}\)
(b) \(\ce{PCl3 + Cl2 ⟶ PCl5}\)
\(\ce{rate}=k\ce{[PCl3][Cl2]}\)
(c) \(\ce{2NO + H2 ⟶ N2 + H2O}\)
\(\ce{rate}=k\ce{[NO][H2]}\)
(d) \(\ce{2NO + O2 ⟶ 2NO2}\)
\(\ce{rate}=k\ce{[NO]^2[O2]}\)
(e) \(\ce{NO + O3 ⟶ NO2 + O2}\)
\(\ce{rate}=k\ce{[NO][O3]}\)
- Solution
-
Add texts here. Do not delete this text first.
An elementary reaction is a chemical reaction in which the reactants directly form products in a single step. In another words, the rate law for the overall reaction is same as experimentally found rate law. Out of 5 options, option (b),(d), and (e) are such reactions
Q12.6.7
Write the rate equation for each of the following elementary reactions:
- \(\ce{O3 \xrightarrow{sunlight} O2 + O}\)
- \(\ce{O3 + Cl ⟶ O2 + ClO}\)
- \(\ce{ClO + O⟶ Cl + O2}\)
- \(\ce{O3 + NO ⟶ NO2 + O2}\)
- \(\ce{NO2 + O ⟶ NO + O2}\)
- Solution
-
Add texts here. Do not delete this text first.
Rate equations are dependent on the reactants and not the products.
The rate law of a reaction can be found using a rate constant (which is found experimentally), and the initial concentrations of reactants.
A general solution for the equation
\(aA + bB \rightarrow cC + dD\)
is \(rate = k[A]^{m}[B]^{n}\) where m and n are reaction orders.
However, reaction orders are found experimentally, and since we do not have experimental data for these reactions, we can disregard that part of the equation.
To find the rate laws, all we have to do is plug the reactants into the rate formula. This is only due to the case that these are elementary reactions. Further reading on elementary reactions can be found on Libre Texts.
a. O3 ⟶ O2 + O
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3]
b. O3 + Cl ⟶ O2 + ClO
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][Cl]
c. ClO + O ⟶ Cl + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[ClO][O]
d. O3 + NO ⟶ NO2 + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][NO]
e. NO2 + O ⟶ NO + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[NO2][O]
- Answer
-
Add texts here. Do not delete this text first.
(a) Rate1 = k[O3]; (b) Rate2 = k[O3][Cl]; (c) Rate3 = k[ClO][O]; (d) Rate2 = k[O3][NO]; (e) Rate3 = k[NO2][O]
Q12.6.8
Nitrogen(II) oxide, NO, reacts with hydrogen, H2, according to the following equation:
\[\ce{2NO + 2H2 ⟶ N2 + 2H2O}\nonumber \]
What would the rate law be if the mechanism for this reaction were:
\[\ce{2NO + H2 ⟶ N2 + H2O2\:(slow)}\nonumber \]
\[\ce{H2O2 + H2 ⟶ 2H2O\:(fast)}\nonumber \]
The rate law of the mechanism is determined by the slow step of the reaction. Since the slow step is an elementary step, the rate law can be drawn from the coefficients of the chemical equation. So therefore, the rate law is as follows: rate=k[NO]2[H2]. Since both NO and H2 are reactants in the overall reaction (therefore are not intermediates in the reaction), no further steps have to be done to determine the rate law.
Q12.6.9
Consider the reaction
CH4 + Cl2 → CH3Cl + HCl (occurs under light)
The mechanism is a chain reaction involving Cl atoms and CH3 radicals. Which of the following steps does not terminate this chain reaction?
- CH3 + Cl → CH3CI
- CH3 + HCl → CH4 + Cl
- CH3 + CH3 → C2H2
- Cl + Cl → Cl2
- Solution
-
Add texts here. Do not delete this text first.
Chain reactions involve reactions that create products necessary for more reactions to occur. In this case, a reaction step will continue the chain reaction if a radical is generated. Radicals are highly reactive particles, so more reactions in the chain will take place as long as they are present. The chlorine is considered a free radical as it has an unpaired electron; for this reason it is very reactive and propagates a chain reaction. It does so by taking an electron from a stable molecule and making that molecule reactive, and that molecule goes on to react with stable species, and in that manner a long series of "chain" reactions are initiated. A chlorine radical will continue the chain by completing the following reaction:
\({Cl \cdot}+{CH_4} \rightarrow {CH_3 \cdot}+{HCl} \)
The \({CH_3}\) generated by this reaction can then react with other species, continuing to propagate the chain reaction.
Option 1 is incorrect because the only species it produces is \({CH_3Cl}\), a product in the overall reaction that is unreactive. This terminates the chain reaction because it fails to produce any \(Cl\) or \(CH_3\) radicals that are necessary for further propagating the overall reaction.
Option 2 is the correct answer because it produces a \(Cl\) radical. This \(Cl\) radical can continue the chain by colliding with \(CH_4\) molecules.
Option 3 is incorrect because it fails to produce a radical capable of continuing the chain.
Option 4 is incorrect because it produces \(Cl_2\), a molecule that does not react unless additional light is supplied. Therefore, this step breaks the chain.
- Answer
-
Add texts here. Do not delete this text first.
Answer: Option 2: \({CH_3}+{HCl} \rightarrow {CH_4}+{Cl}\)
Q12.6.10
Experiments were conducted to study the rate of the reaction represented by this equation.
\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]
Initial concentrations and rates of reaction are given here.
| Experiment | Initial Concentration [NO] (mol/L) | Initial Concentration, [H2] (mol/L) | Initial Rate of Formation of N2 (mol/L min) |
|---|---|---|---|
| 1 | 0.0060 | 0.0010 | 1.8 × 10−4 |
| 2 | 0.0060 | 0.0020 | 3.6 × 10−4 |
| 3 | 0.0010 | 0.0060 | 0.30 × 10−4 |
| 4 | 0.0020 | 0.0060 | 1.2 × 10−4 |
Consider the following questions:
- Determine the order for each of the reactants, NO and H2, from the data given and show your reasoning.
- Write the overall rate law for the reaction.
- Calculate the value of the rate constant, k, for the reaction. Include units.
- For experiment 2, calculate the concentration of NO remaining when exactly one-half of the original amount of H2 had been consumed.
- The following sequence of elementary steps is a proposed mechanism for the reaction.
Step 1: \(\ce{NO + NO ⇌ N2O2}\)
Step 2: \(\ce{N2O2 + H2 ⇌ H2O + N2O}\)
Step 3: \(\ce{N2O + H2 ⇌ N2 + H2O}\)
Based on the data presented, which of these is the rate determining step? Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.
S12.6.10
1. i) Find the order for [NO] by using experiment 3 and 4 where [H2] is constant
Notice that [NO] doubles from experiment 3 to 4 and the rate quadruples. So the order for [NO] is 2
ii) Find the order for [H2] by using experiment 1 and 2 where [NO] is constant
Notice that [H2] doubles from experiment 1 to 2 and the rate doubles as well. So the order for [H2] is 1
2. Put in the order for each product as the exponents for the corresponding reactant.
\(rate = k [NO]^2 [H_2]\)
3. Put in the concentrations and the rate from one of the experiments into the rate law and solve for k. (Here, experiement 1 is used but any of them will work)
\(rate = k [NO]^2 [H_2]\) \(.00018 = k [.006]^2 [.001]\) \(k = 5000 M^{-2}s^{-1}\)
4. Plug in values for experiment 2 into the rate law equation and solve for the concentration of NO
\(.00036=5000[NO]^2[.001]\) \([NO]^2= 7.2 x 10^{-5}\) \([NO] = .0085 M\)
5. Write the rate laws for each step and then see which matches the rate law we found in question 2. The rate determining step (the slow step) is the one that gives the rate for the overall reaction. Because of this, only those concentrations will influence the overall reaction, contrary to what we would believe if we just looked at the overall reaction.
Step 1: \(NO + NO \rightleftharpoons N_2O_2\)
\(rate =k_1[NO]^2\) This rate law is not the same as the one we calculate in question 2 so this can not be the rate determining step
Step 2: \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\)
\(rate = k_2[N_2O_2][H_2]\)
Since \(N_2O_2\) is an intermediate you must replace it in the rate law equation. Intermediates can not be in the rate law because they do not appear in the overall reaction. Here you can take the reverse of equation 1 (k-1) and substitute the other side (the reactants of equation 1) for the intermediate in the rate law equation.
\[rate_1 = rate_{-1}\nonumber \]
\[k_1[NO]^2 = k_{-1}[N_2O_2]\nonumber \]
\[[N_2O_2] = \frac{k_1[NO]^2}{k_{-1}}\nonumber \]
\(rate= \frac{k_2k_{1}[NO]^2[H_2]}{k_{-1}}\)
Overall: \(rate={k[NO]^2[H_2]}\) This is the same so it is the rate determining step.
So \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\) is the rate determining step step.
- Answer
-
Add texts here. Do not delete this text first.
(a) NO: 2
\(\ce {H2}\) : 1
(b) Rate = k [NO]2[H2];
(c) k = 5.0 × 103 mol−2 L−2 min−1;
(d) 0.0050 mol/L;
(e) Step II is the rate-determining step.
Q12.6.11
The reaction of CO with Cl2 gives phosgene (COCl2), a nerve gas that was used in World War I. Use the mechanism shown here to complete the following exercises:
- \(\ce{Cl2}(g)⇌\ce{2Cl}(g)\) (fast, k1 represents the forward rate constant, k−1 the reverse rate constant)
- \(\ce{CO}(g)+\ce{Cl}(g)⟶\ce{COCl}(g)\) (slow, k2 the rate constant)
- \(\ce{COCl}(g)+\ce{Cl}(g)⟶\ce{COCl2}(g)\) (fast, k3 the rate constant)
- Write the overall reaction.
- Identify all intermediates.
- Write the rate law for each elementary reaction.
- Write the overall rate law expression.
- Solution
-
Add texts here. Do not delete this text first.
1. To write the overall reaction you have to identify the intermediates and leave them out. The easiest way to do this is to write out all the products and reactants and cross out anything that is on both sides.
Cl2(g) + CO(g) + 2Cl(g) +COCl(g) ⇒ 2Cl(g) + COCl(g) + COCl2(g)
In this you will cross out the 2Cl(g) molecules and the COCl(g). What is left after that is the overall reaction.
Cl2(g) + CO(g) ⇒ + COCl2(g)
2. For part two you will just list the intermediates that you crossed out.
Cl and COCl are intermediates
3. Each rate law will be the rate equal to the rate constant times the concentrations of the reactants
reaction 1
(forward) rate=k1[Cl2] ( reverse) rate=k-1[Cl]
reaction 2
rate=k2[CO][Cl]
Reaction 3
rate=k3[COCl][Cl]
4. The overall rate law is based off the slowest step (step #2), since it is the rate determining step, but Cl is present in that rate law so we have to replace it with an equivalent that does not contain an intermediate. To do this you use the equilibrium since the rates are the same you can set up the rate laws of the forward and reverse equal to each other.
k1[Cl2] = k-1[Cl]
[Cl]= k1[Cl2]/k-1
rate=k2[CO]k1[Cl2]/k-1
rate=k°[CO][Cl2]
Steps to replacing and intermediate
- Set the forward and reverse reaction equal to each other using separate constants
- Solve for the intermediate using algebra
- Plug into the rate determining formula
- All the k's will be condensed into a K prime constant
12.7: Catalysis
Q12.7.1
Account for the increase in reaction rate brought about by a catalyst.
Q12.7.2
Compare the functions of homogeneous and heterogeneous catalysts.
Q12.7.3
Consider this scenario and answer the following questions: Chlorine atoms resulting from decomposition of chlorofluoromethanes, such as CCl2F2, catalyze the decomposition of ozone in the atmosphere. One simplified mechanism for the decomposition is: \[\ce{O3 \xrightarrow{sunlight} O2 + O}\\ \ce{O3 + Cl ⟶ O2 + ClO}\\ \ce{ClO + O ⟶ Cl + O2}\nonumber \]
- Explain why chlorine atoms are catalysts in the gas-phase transformation: \[\ce{2O3⟶3O2}\nonumber \]
- Nitric oxide is also involved in the decomposition of ozone by the mechanism: \[\ce{O3 \xrightarrow{sunlight} O2 + O\\ O3 + NO ⟶ NO2 + O2\\ NO2 + O ⟶ NO + O2}\nonumber \]
Is NO a catalyst for the decomposition? Explain your answer.
Q12.7.4
For each of the following pairs of reaction diagrams, identify which of the pair is catalyzed:
(a)
Q12.7.5
For each of the following pairs of reaction diagrams, identify which of the pairs is catalyzed:
(a)
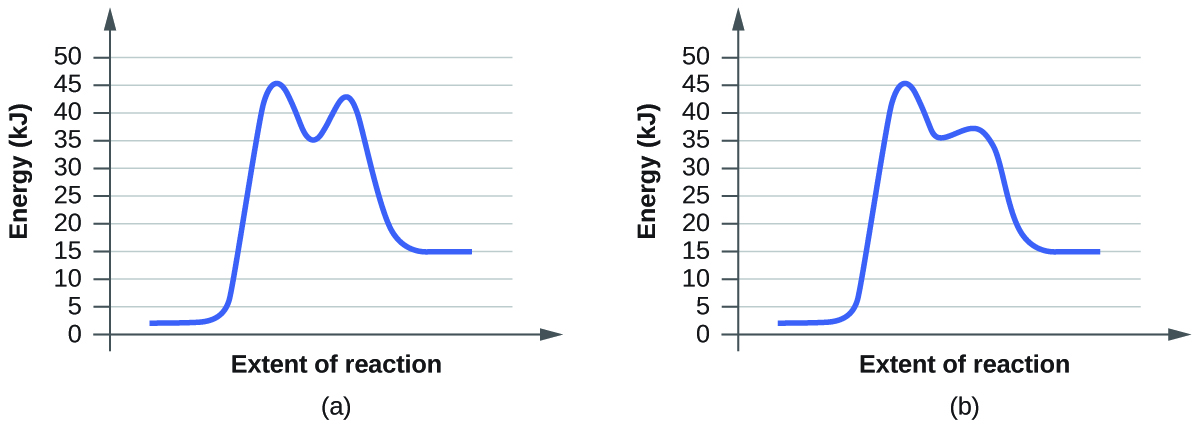
(b)
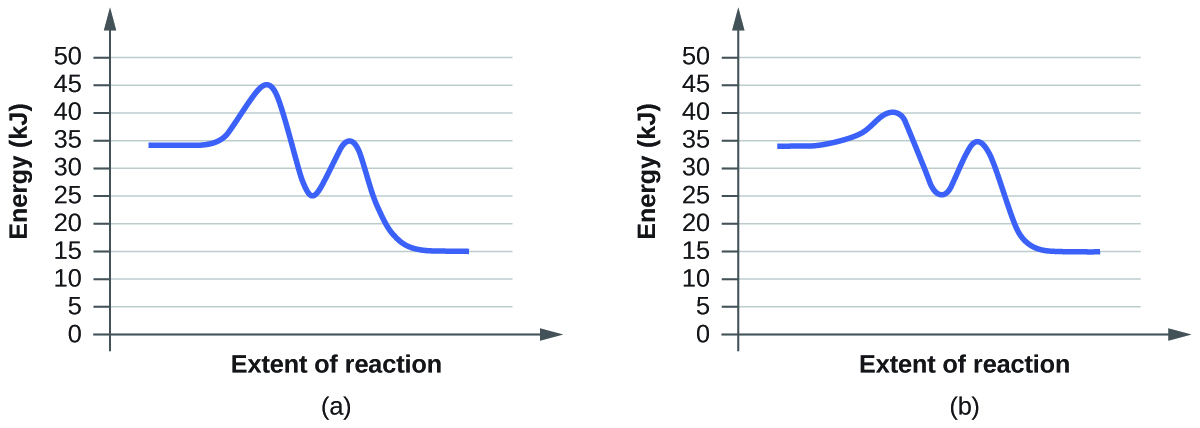
Q12.7.6
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)
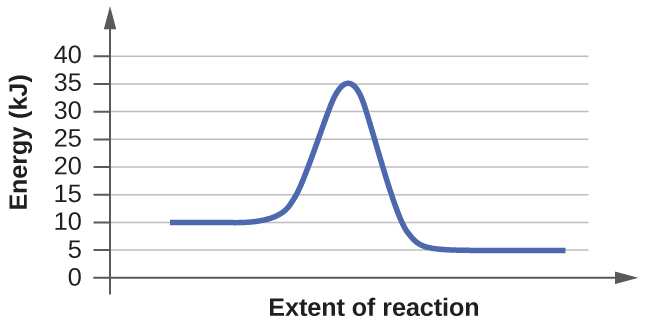
(b)
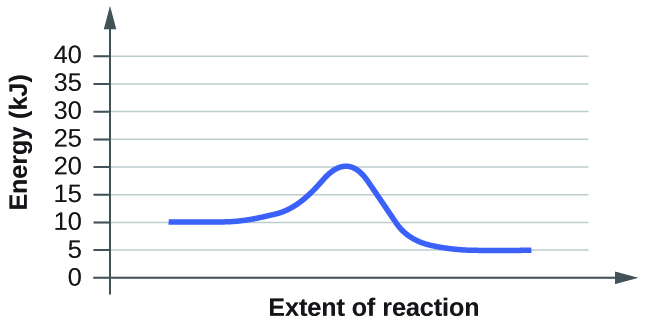
Q12.7.7
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)

(b)
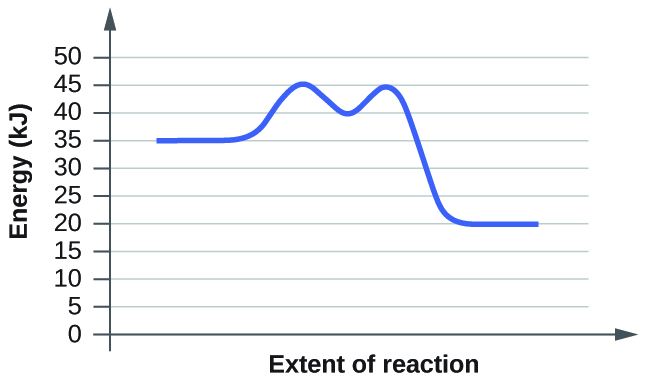
Q12.7.8
- Based on the diagrams in Question Q12.7.6, which of the reactions has the fastest rate? Which has the slowest rate?
- Based on the diagrams in Question Q12.7.7, which of the reactions has the fastest rate? Which has the slowest rate?



![{\ estilo de exibição t_ {\ frac {1} {2}} = {\ frac {1} {k {\ ce {[A] 0}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b25f9b5e7675b3e3f9027241a74ec2d751810c43)