12.5: Teoria da colisão

Last updated
Save as PDF

Page ID: 184996

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Use os postulados da teoria da colisão para explicar os efeitos do estado físico, temperatura e concentração nas taxas de reação
Defina os conceitos de energia de ativação e estado de transição
Use a equação de Arrhenius em cálculos relacionando constantes de taxa à temperatura

Não devemos nos surpreender que átomos, moléculas ou íons colidam antes que possam reagir uns com os outros. Os átomos devem estar próximos para formar ligações químicas. Essa premissa simples é a base de uma teoria muito poderosa que explica muitas observações sobre a cinética química, incluindo fatores que afetam as taxas de reação. A teoria da colisão é baseada nos seguintes postulados:

Postulados da teoria da colisão

A taxa de uma reação é proporcional à taxa de colisões do reagente:\[\mathrm{reaction\: rate ∝ \dfrac{\#\,collisions}{time}} \nonumber \]
As espécies que reagem devem colidir em uma orientação que permita o contato entre os átomos que se unirão no produto.
A colisão deve ocorrer com energia adequada para permitir a penetração mútua das camadas de valência da espécie reagente para que os elétrons possam se reorganizar e formar novas ligações (e novas espécies químicas).

Podemos ver a importância dos dois fatores físicos observados nos postulados 2 e 3, a orientação e a energia das colisões, quando consideramos a reação do monóxido de carbono com o oxigênio:

\[\ce{2CO}(g)+\ce{O2}(g)⟶\ce{2CO2}(g) \nonumber \]

O monóxido de carbono é um poluente produzido pela combustão de combustíveis de hidrocarbonetos. Para reduzir esse poluente, os automóveis têm conversores catalíticos que usam um catalisador para realizar essa reação. É também uma reação colateral da combustão da pólvora que resulta em flash de focinho para muitas armas de fogo. Se o monóxido de carbono e o oxigênio estiverem presentes em quantidade suficiente, a reação é espontânea em alta temperatura e pressão.

O primeiro passo na reação em fase gasosa entre monóxido de carbono e oxigênio é uma colisão entre as duas moléculas:

\[\ce{CO}(g)+\ce{O2}(g)⟶\ce{CO2}(g)+\ce{O}(g) \nonumber \]

Embora existam muitas orientações possíveis diferentes que as duas moléculas podem ter em relação uma à outra, considere as duas apresentadas na Figura\(\PageIndex{1}\). No primeiro caso, o lado do oxigênio da molécula de monóxido de carbono colide com a molécula de oxigênio. No segundo caso, o lado do carbono da molécula de monóxido de carbono colide com a molécula de oxigênio. O segundo caso é claramente mais provável de resultar na formação de dióxido de carbono, que tem um átomo de carbono central ligado a dois átomos de oxigênio\(\ce{(O=C=O)}\). Este é um exemplo bastante simples da importância da orientação da colisão em termos de criação do produto desejado da reação.

alt — Figura\(\PageIndex{1}\): Ilustradas estão duas colisões que podem ocorrer entre as moléculas de monóxido de carbono e oxigênio. A orientação das moléculas em colisão determina parcialmente se uma reação entre as duas moléculas ocorrerá.

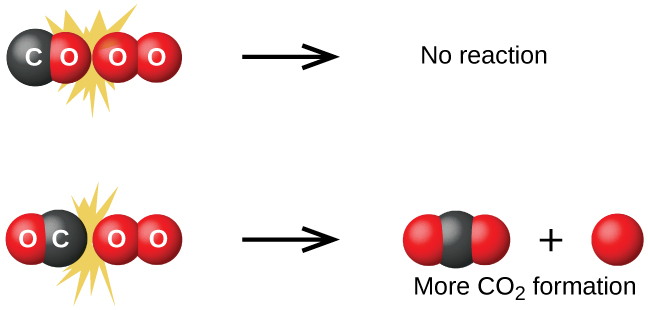
Se a colisão ocorrer com a orientação correta, ainda não há garantia de que a reação continuará formando dióxido de carbono. Cada reação requer uma certa quantidade de energia de ativação para prosseguir na direção direta, produzindo um complexo ativado apropriado ao longo do caminho. Como\(\PageIndex{2}\) demonstra a Figura, mesmo uma colisão com a orientação correta pode falhar em formar o produto da reação. No estudo dos mecanismos de reação, cada um desses três arranjos de átomos é chamado de complexo ativado proposto ou estado de transição.

alt — Figura\(\PageIndex{2}\): Possíveis estados de transição (complexos ativados) para o monóxido de carbono reagindo com o oxigênio para formar dióxido de carbono. Linhas sólidas representam ligações covalentes, enquanto linhas pontilhadas representam sobreposições orbitais instáveis que podem, ou não, se tornar ligações covalentes à medida que o produto é formado. Nos dois primeiros exemplos desta figura, a ligação dupla O = O não é afetada; portanto, o dióxido de carbono não pode se formar. O terceiro estado de transição proposto resultará na formação de dióxido de carbono se o terceiro átomo de oxigênio “extra” se separar do resto da molécula.

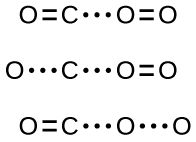
Na maioria das circunstâncias, é impossível isolar ou identificar um estado de transição ou complexo ativado. Na reação entre monóxido de carbono e oxigênio para formar dióxido de carbono, complexos ativados só foram observados espectroscopicamente em sistemas que utilizam um catalisador heterogêneo. A reação em fase gasosa ocorre muito rapidamente para isolar qualquer composto químico desse tipo.

A teoria da colisão explica por que a maioria das taxas de reação aumenta com o aumento das concentrações. Com o aumento da concentração de qualquer substância reagente, as chances de colisões entre moléculas aumentam porque há mais moléculas por unidade de volume. Mais colisões significam uma taxa de reação mais rápida, supondo que a energia das colisões seja adequada.

Energia de ativação e a equação de Arrhenius

A energia mínima necessária para formar um produto durante uma colisão entre reagentes é chamada de energia de ativação y (\(E_a\)). A energia cinética das moléculas reagentes desempenha um papel importante em uma reação porque a energia necessária para formar um produto é fornecida pela colisão de uma molécula reagente com outra molécula reagente. (Em reações de reagente único, a energia de ativação pode ser fornecida por uma colisão da molécula do reagente com a parede do recipiente de reação ou com moléculas de um contaminante inerte.) Se a energia de ativação for muito maior do que a energia cinética média das moléculas, a reação ocorrerá lentamente: apenas algumas moléculas em movimento rápido terão energia suficiente para reagir. Se a energia de ativação for muito menor do que a energia cinética média das moléculas, a fração das moléculas que possuem a energia cinética necessária será grande; a maioria das colisões entre as moléculas resultará em reação e a reação ocorrerá rapidamente.

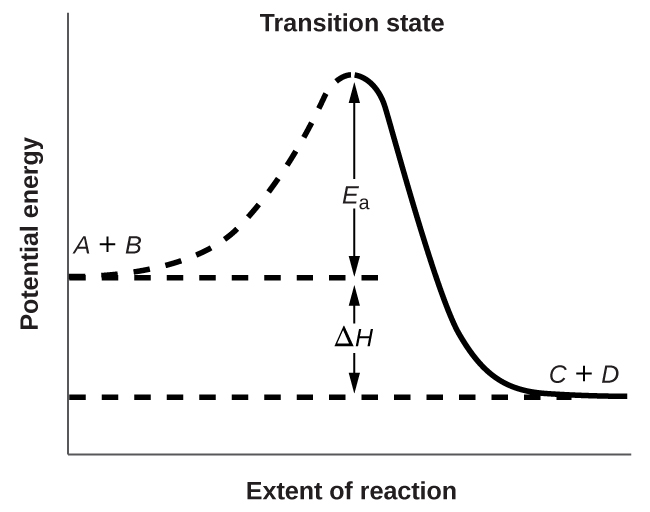
A figura\(\PageIndex{3}\) mostra as relações de energia para a reação geral de uma molécula de\(A\) com uma molécula de\(B\) para formar moléculas de\(C\) e\(D\):

\[A+B⟶C+D \nonumber \]

A figura mostra que a energia do estado de transição é maior que a dos reagentes\(A\) e\(B\) em quantidade igual à\(E_a\) energia de ativação. Assim, a soma das energias cinéticas de\(A\) e\(B\) deve ser igual ou maior que E _a para alcançar o estado de transição. Depois que o estado de transição é atingido\(C\) e\(D\) começa a se formar, o sistema perde energia até que sua energia total seja menor que a da mistura inicial. Essa energia perdida é transferida para outras moléculas, dando-lhes energia suficiente para alcançar o estado de transição. A reação direta (aquela entre as moléculas\(A\) e\(B\)), portanto, tende a ocorrer rapidamente uma vez que a reação tenha começado. Na Figura\(\PageIndex{3}\),\(ΔH\) representa a diferença na entalpia entre os reagentes (\(A\)e\(B\)) e os produtos (\(C\)e\(D\)). A soma de\(E_a\) e\(ΔH\) representa a energia de ativação para a reação inversa:

\[C+D⟶A+B \nonumber \]

alt — Figura\(\PageIndex{3}\): Este gráfico mostra as relações potenciais de energia para a reação\(A+B⟶C+D\). A porção tracejada da curva representa a energia do sistema com uma molécula de A e uma molécula de B presentes, e a porção sólida a energia do sistema com uma molécula de C e uma molécula de D presentes. A energia de ativação para a reação direta é representada por E _a. A energia de ativação para a reação reversa é maior do que a da reação direta em uma quantidade igual a ΔH. O pico da curva representa o estado de transição.

Podemos usar a equação de Arrhenius para relacionar a energia de ativação e a constante de taxa, k, de uma determinada reação:

\[k=Ae^{−E_a/RT} \label{Arrhenius} \]

Nessa equação,

\(R\)é a constante de gás ideal, que tem um valor 8,314 J/mol/K,
\(T\)é a temperatura na escala Kelvin,
\(E_a\)é a energia de ativação em joules por mol,
\(e\)é a constante 2,7183, e
\(A\)é uma constante chamada fator de frequência, que está relacionada à frequência das colisões e à orientação das moléculas que reagem.

Ambos os postulados da teoria de colisão das taxas de reação são acomodados na equação de Arrhenius. O fator de frequência A está relacionado à taxa na qual as colisões com a orientação correta ocorrem. O termo exponencial,\(e^{−E_a/RT}\), está relacionado à fração de colisões que fornece energia adequada para superar a barreira de ativação da reação.

Em um extremo, o sistema não contém energia suficiente para que as colisões superem a barreira de ativação. Nesses casos, nenhuma reação ocorre. No outro extremo, o sistema tem tanta energia que toda colisão com a orientação correta pode superar a barreira de ativação, fazendo com que a reação prossiga. Nesses casos, a reação é quase instantânea.

A equação de Arrhenius (Equação\ ref {Arrhenius}) descreve quantitativamente muito do que já discutimos sobre taxas de reação. Para duas reações na mesma temperatura, a reação com maior energia de ativação tem a menor taxa constante e a taxa mais lenta. O maior valor de\(E_a\) resulta em um valor menor para\(e^{−E_a/RT}\), refletindo a menor fração de moléculas com energia suficiente para reagir. Alternativamente, a reação com a menor\(E_a\) tem uma fração maior de moléculas com energia suficiente para reagir. Isso será refletido como um valor maior de\(e^{−E_a/RT}\), uma constante de taxa maior e uma taxa mais rápida para a reação.

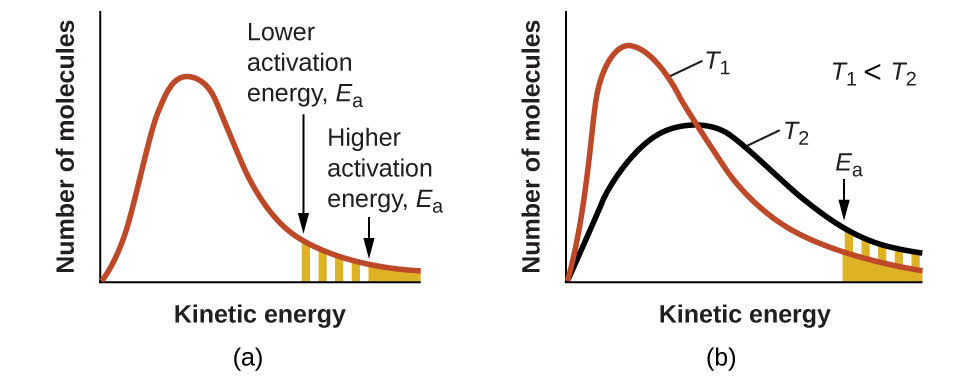
Figura\(\PageIndex{4}\): (a) À medida que a energia de ativação de uma reação diminui, o número de moléculas com pelo menos essa energia aumenta, conforme mostrado pelas áreas sombreadas. (b) Em uma temperatura mais alta, T2, mais moléculas têm energias cinéticas maiores que Ea, conforme mostrado pela área sombreada em amarelo.

Um aumento na temperatura tem o mesmo efeito que uma diminuição na energia de ativação. Uma fração maior das moléculas tem a energia necessária para reagir (Figura\(\PageIndex{4}\)), conforme indicado por um aumento no valor de\(e^{−E_a/RT}\). A constante de taxa também é diretamente proporcional ao fator de frequência,\(A\). Portanto, uma mudança nas condições ou reagentes que aumenta o número de colisões com uma orientação favorável para a reação resulta em um aumento\(A\) e, consequentemente, em um aumento de\(k\).

Uma abordagem conveniente\(E_a\) para determinar uma reação envolve a medição de\(k\) em diferentes temperaturas e o uso de uma versão alternativa da equação de Arrhenius que assume a forma de uma equação linear:

\ [\ begin {align*}
\ ln k&=\ left (\ dfrac {−e_A} {R}\ right)\ left (\ dfrac {1} {T}\ right) +\ ln A\\
y&=mx+b
\ end {align*}\ nonumber\]

Assim, um gráfico de\(\ln k\) versus\(\dfrac{1}{T}\) fornece uma linha reta com a inclinação\(\dfrac{-E_\ce{a}}{R}\), a partir da qual E _a pode ser determinada. O intercepto fornece o valor de\(\ln A\). Às vezes, isso é chamado de conspiração de Arrhenius.

Exemplo\(\PageIndex{1}\)

Determinação _de E a A variação da taxa constante com a temperatura para a decomposição de HI (g) em H ₂ (g) e I ₂ (g) é dada aqui. Qual é a energia de ativação da reação?

\[\ce{2HI}(g)⟶\ce{H2}(g)+\ce{I2}(g) \nonumber \]

variação da taxa constante com a temperatura para a decomposição de HI (g) em H2 (g) e I2 (g)
T (K)	k (L/mol/s)
555	3,52 × 10 ⁻⁷
575	1,2 × 10 ⁻⁶
645	8,59 × 10 ⁻⁵
700	1,16 × 10 ⁻³
781	3,95 × 10 ⁻²

Solução

Os valores de\(\dfrac{1}{T}\) e ln k são:

Soluções para o exemplo 12.5.1
\(\mathrm{\dfrac{1}{T}\:(K^{−1})}\)	em k
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)” style="text-align:center; ">1,80 × 10 ⁻³	−14.860
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)” style="text-align:center; ">1,74 × 10 ⁻³	−13,617
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)” style="text-align:center; ">1,55 × 10 ⁻³	−9,362
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)” style="text-align:center; ">1,43 × 10 ⁻³	−6,759
\ (\ mathrm {\ dfrac {1} {T}\: (K^ {−1})}\)” style="text-align:center; ">1,28 × 10 ⁻³	−3,231

A figura\(\PageIndex{5}\) é um gráfico de ln k versus\(\dfrac{1}{T}\). Para determinar a inclinação da linha, precisamos de dois valores de ln k, que são determinados a partir da linha em dois valores de\(\dfrac{1}{T}\) (um próximo a cada extremidade da linha é preferível). Por exemplo, o valor de ln k determinado a partir da linha quando\(\dfrac{1}{T}=1.25×10^{−3}\) é −2,593; o valor quando\(\dfrac{1}{T}=1.78×10^{−3}\) é −14,447.

alt — Figura\(\PageIndex{5}\): Este gráfico mostra a relação linear entre\(\ln k\) e\(\dfrac{1}{T}\) para a reação de\(\ce{2HI ⟶ H2 + I2}\) acordo com a equação de Arrhenius.

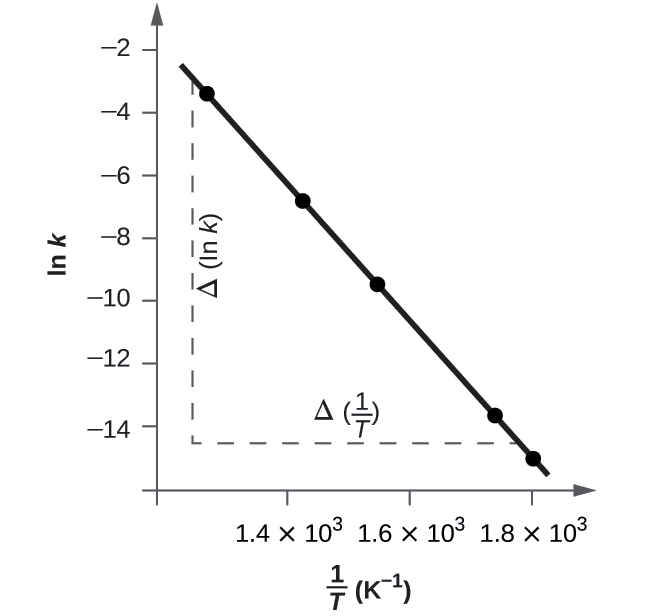
A inclinação dessa linha é dada pela seguinte expressão:

\ [\ begin {align*}
\ ce {Inclinação} &=\ dfrac {δ (\ ln k)} {Δ\ left (\ dfrac {1} {T}\ right)}\\
&=\ mathrm {\ dfrac {(−14.447) − (−2,593)} {(1,78×10^ {−3}\ :K^ {−1}) − (1,25×10^ {−3}\ :K^ {−1})}}\\
&=\ mathrm {\ dfrac {−11,854} {0,53×10^ {−3}\ :K^ {−1}} =2,2 × 10^4\ :K}\\
&=−\ dfrac {E_\ ce {a}} {R}
\ end {align*}\ nonumber\]

Assim:

\[ \begin{align*} E_\ce{a} &=\mathrm{−slope×\mathit R=−(−2.2×10^4\:K×8.314\: J\: mol^{−1}\:K^{−1})} \\[4pt] &=\mathrm{1.8×10^5\:J\: mol^{−1}} \end{align*} \nonumber \]

Em muitas situações, é possível obter uma estimativa razoável da energia de ativação sem passar por todo o processo de construção do gráfico de Arrhenius. A equação de Arrhenius:

\[\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A \nonumber \]

pode ser reorganizado conforme mostrado para fornecer:

\[\dfrac{Δ(\ln k)}{Δ\left(\dfrac{1}{T}\right)}=−\dfrac{E_\ce{a}}{R} \nonumber \]

\[\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right) \nonumber \]

Essa equação pode ser reorganizada para fornecer um cálculo em uma etapa para obter uma estimativa da energia de ativação:

\[E_\ce{a}=−R\left( \dfrac{\ln k_2−\ln k_1}{\left(\dfrac{1}{T_2}\right)−\left(\dfrac{1}{T_1}\right)}\right ) \nonumber \]

Usando os dados experimentais apresentados aqui, podemos simplesmente selecionar duas entradas de dados. Para este exemplo, selecionamos a primeira e a última entrada:

Primeira e última entrada
T (K)	k (L/mol/s)	\(\dfrac{1}{T}\:(K^{-1})\)	em k
555	3,52 × 10 ⁻⁷	\ (\ dfrac {1} {T}\: (K^ {-1})\)” style="text-align:center; ">1,80 × 10 ⁻³	−14.860
781	3,95 × 10 ⁻²	\ (\ dfrac {1} {T}\: (K^ {-1})\)” style="text-align:center; ">1,28 × 10 ⁻³	−3,231

Depois de calcular\(\dfrac{1}{T}\) e ln k, podemos substituir na equação:

\[E_\ce{a}=\mathrm{−8.314\:J\:mol^{−1}\:K^{−1}\left(\dfrac{−3.231−(−14.860)}{1.28×10^{−3}\:K^{−1}−1.80×10^{−3}\:K^{−1}}\right)} \nonumber \]

e o resultado é E _a = 185.900 J/mol.

Esse método é muito eficaz, especialmente quando um número limitado de constantes de taxa dependentes da temperatura estão disponíveis para a reação de interesse.

Exercício\(\PageIndex{1}\)

A taxa constante para a taxa de decomposição de N ₂ O ₅ em NO e O ₂ na fase gasosa é de 1,66 L/mol/s a 650 K e 7,39 L/mol/s a 700 K:

\[\ce{2N2O5}(g)⟶\ce{4NO}(g)+\ce{3O2}(g) \nonumber \]

Supondo que a cinética dessa reação seja consistente com a equação de Arrhenius, calcule a energia de ativação para essa decomposição.

Responda: 113.000 J/mol

Resumo

As reações químicas requerem colisões entre espécies reagentes. Essas colisões de reagentes devem ter orientação adequada e energia suficiente para resultar na formação do produto. A teoria da colisão fornece uma explicação simples, mas eficaz, para o efeito de muitos parâmetros experimentais nas taxas de reação. A equação de Arrhenius descreve a relação entre a constante de taxa de uma reação e sua energia de ativação, temperatura e dependência da orientação da colisão.

Equações-chave

\(k=Ae^{−E_a/RT}\)
\(\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A\)
\(\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right)\)

Glossário

complexo ativado: (também, estado de transição) combinação instável de espécies reagentes representando o estado de energia mais alto de um sistema de reação

energia de ativação (E _a): energia necessária para que uma reação ocorra

Equação de Arrhenius: relação matemática entre a constante de taxa e a energia de ativação de uma reação

teoria da colisão: modelo que enfatiza a energia e a orientação das colisões moleculares para explicar e prever a cinética da reação

fator de frequência (A): constante de proporcionalidade na equação de Arrhenius, relacionada ao número relativo de colisões com uma orientação capaz de levar à formação do produto