12.4: Leis tarifárias integradas
- Page ID
- 184960
- Explicar a forma e a função de uma lei de taxas integrada
- Execute cálculos integrados da lei de taxas para reações de zero, primeira e segunda ordem
- Defina a meia-vida e realize cálculos relacionados
- Identifique a ordem de uma reação a partir dos dados de concentração/tempo
As leis de taxas que vimos até agora relacionam a taxa e as concentrações de reagentes. Também podemos determinar uma segunda forma de cada lei de taxas que relaciona as concentrações de reagentes e o tempo. Essas são chamadas de leis tarifárias integradas. Podemos usar uma lei de taxa integrada para determinar a quantidade de reagente ou produto presente após um período de tempo ou para estimar o tempo necessário para que uma reação prossiga até certo ponto. Por exemplo, uma lei de taxa integrada é usada para determinar o período de tempo que um material radioativo deve ser armazenado para que sua radioatividade decaia para um nível seguro.
Usando o cálculo, a lei de taxa diferencial para uma reação química pode ser integrada em relação ao tempo para fornecer uma equação que relaciona a quantidade de reagente ou produto presente em uma mistura de reação com o tempo decorrido da reação. Esse processo pode ser muito simples ou muito complexo, dependendo da complexidade da lei da taxa diferencial. Para fins de discussão, vamos nos concentrar nas leis de taxas integradas resultantes para reações de primeira, segunda e ordem zero.
Reações de primeira ordem
Uma equação relacionando a constante de taxa com\(k\) a concentração inicial\([A]_0\) e a concentração\([A]_t\) presente após um determinado tempo\(t\) pode ser derivada para uma reação de primeira ordem e mostrada como sendo:
\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber \]
ou alternativamente
\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber \]
ou
\[[A]=[A]_0e^{−kt} \nonumber \]
A constante de taxa para a decomposição de primeira ordem do ciclobutano,\(\ce{C4H8}\) a 500 °C, é 9,2 × 10 −3 s −1:
\[\ce{C4H8⟶2C2H4} \nonumber \]
Quanto tempo levará para que 80,0% de uma amostra de C 4 H 8 se decomponha?
Solução
Usamos a forma integrada da lei de taxas para responder perguntas sobre o tempo:
\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber \]
Existem quatro variáveis na lei de taxas, então, se conhecermos três delas, podemos determinar a quarta. Nesse caso, sabemos [A] 0, [A] e k e precisamos encontrar t.
A concentração inicial de C 4 H 8, [A] 0, não é fornecida, mas a provisão de que 80,0% da amostra tenha se decomposto é informação suficiente para resolver esse problema. Seja x a concentração inicial, caso em que a concentração após 80,0% de decomposição é 20,0% de x ou 0,200 x. Reorganizar a lei da taxa para isolar t e substituir as quantidades fornecidas produz:
\ [\ begin {align*}
t&=\ ln\ dfrac {[x]} {[0,200x]} ×\ dfrac {1} {k}\\ [4pt]
&=\ mathrm {\ ln\ dfrac {0,100\ :mol\: L^ {−1}} {0.020\ :mol\: L^ {−1}} ×\ dfrac c {1} {9,2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ mathrm {1,609×\ dfrac {1} {9,2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ mathrm {1,7 × 10^ 2\ :s}
\ end {align*}\ nonumber\]
O iodo-131 é um isótopo radioativo usado para diagnosticar e tratar algumas formas de câncer de tireoide. O iodo-131 decai para xenônio-131 de acordo com a equação:
\[\textrm{I-131 ⟶ Xe-131 + electron} \nonumber \]
O decaimento é de primeira ordem com uma constante de taxa de 0,138 d −1. Todo decaimento radioativo é de primeira ordem. Quantos dias serão necessários para que 90% do iodo-131 em uma solução de 0,500 M dessa substância se decomponha para Xe-131?
- Resposta
-
16,7 dias
Podemos usar leis de taxa integradas com dados experimentais que consistem em informações de tempo e concentração para determinar a ordem e a constante de taxa de uma reação. A lei de taxas integrada pode ser reorganizada para um formato de equação linear padrão:
\ [\ begin {align}
\ ln [A] & =( −k) (t) +\ ln [A] _0\ label {in1st}\\ [4pt]
y&=mx+b
\ end {align}\ nonumber\]
Um gráfico de\(\ln[A]\) versus\(t\) para uma reação de primeira ordem é uma linha reta com uma inclinação de\(−k\) e uma interceptação de\(\ln[A]_0\). Se um conjunto de dados de taxa for plotado dessa forma, mas não resultar em uma linha reta, a reação não será de primeira ordem\(A\).
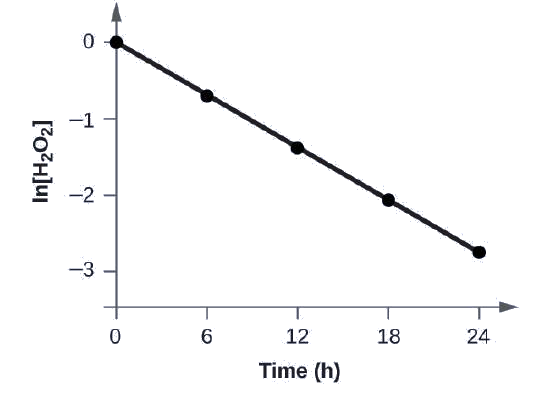
Mostre que os dados nesta Figura podem ser representados por uma lei de taxa de primeira ordem representando graficamente ln [H 2 O 2] versus tempo. Determine a constante de taxa para a taxa de decomposição de H 2 O 2 a partir desses dados.
Solução
Os dados desta Figura com a adição de valores de ln [H 2 O 2] são dados na Figura\(\PageIndex{1}\).
| Ensaio | Tempo (h) | [H 2 OU 2] (MM) | em [H 2 O 2] |
|---|---|---|---|
| 1 | 0 | 1.000 | 0,0 |
| 2 | 6,00 | 0,500 | −0,693 |
| 3 | 12,00 | 0,250 | −1,386 |
| 4 | 18,00 | 0,125 | −2,079 |
| 5 | 24,00 | 0,0625 | −2,72 |
O gráfico de ln [H 2 O 2] versus tempo é linear, portanto, verificamos que a reação pode ser descrita por uma lei de taxa de primeira ordem.
A constante de taxa para uma reação de primeira ordem é igual ao negativo da inclinação do gráfico de ln [H 2 O 2] versus o tempo em que:
\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber \]
Para determinar a inclinação da reta, precisamos de dois valores de ln [H 2 O 2] em valores diferentes de t (um próximo a cada extremidade da linha é preferível). Por exemplo, o valor de ln [H 2 O 2] quando t é 6,00 h é −0,693; o valor quando t = 12,00 h é −1,386:
\ [\ begin {align*}
\ ce {inclinação} &=\ mathrm {\ dfrac {−1,386− (−0,693)} {12,00\: h−6,00\: h}}\ [4pt]
&=\ mathrm {\ dfrac {−0,693} {6,00\: h}}\\ [4pt]
&=\ mathrm {−1,15×10^ {−2}\ :h^ {−1}}\\ [4pt]
k&=\ mathrm {−slope=− (−1,155 × 10^ {−1}\ :h^ {−1}) =1,155 × 10^ {−1}\ :h^ {−1} }
\ end {align*}\ nonumber\]
Faça um gráfico dos seguintes dados para determinar se a reação\(A⟶B+C\) é de primeira ordem.
| Ensaio | Hora (s) | [UM] |
|---|---|---|
| 1 | 4,0 | 0,220 |
| 2 | 8.0 | 0,144 |
| 3 | 12,0 | 0,110 |
| 4 | 16,0 | 0,088 |
| 5 | 20,0 | 0,074 |
- Resposta
-
O gráfico de ln [A] versus t não é uma linha reta. A equação não é de primeira ordem:
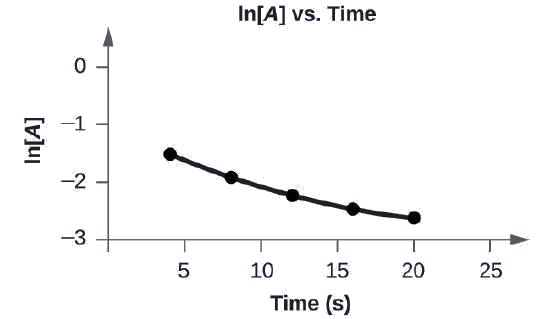
Um gráfico, rotulado acima como “l n [A] versus Tempo” é exibido. O eixo x é rotulado como “Tempo (s)” e o eixo y é rotulado como “l n [A]”. O eixo x mostra marcações em 5, 10, 15, 20 e 25 horas. O eixo y mostra marcações em menos 3, menos 2, menos 1 e 0. Uma pequena curva é desenhada conectando cinco pontos em coordenadas de aproximadamente (4, menos 1,5), (8, menos 2), (12, menos 2,2), (16, menos 2,4) e (20, menos 2,6).
Reações de segunda ordem
As equações que relacionam as concentrações de reagentes e a constante de taxa das reações de segunda ordem são bastante complicadas. Vamos nos limitar às reações mais simples de segunda ordem, ou seja, aquelas com taxas que dependem da concentração de apenas um reagente e descritas pela lei da taxa diferencial:
\[\ce{Rate}=k[A]^2 \nonumber \]
Para essas reações de segunda ordem, a lei de taxas integradas é:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd} \]
onde os termos na equação têm seus significados usuais, conforme definido anteriormente.
A reação do gás butadieno (C 4 H 6) consigo mesmo produz gás C 8 H 12 da seguinte forma:
\[\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber \]
A reação é de segunda ordem com uma taxa constante igual a 5,76 × 10 −2 L/mol/min sob certas condições. Se a concentração inicial de butadieno for 0,200 M, qual é a concentração restante após 10,0 min?
Solução
Usamos a forma integrada da lei de taxas para responder perguntas sobre o tempo. Para uma reação de segunda ordem, temos:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
Conhecemos três variáveis nessa equação: [A] 0 = 0,200 mol/L, k = 5,76 × 10 −2 L/mol/min e t = 10,0 min. Portanto, podemos resolver para [A], a quarta variável:
\ [\ begin {align*}
\ dfrac {1} {[A]} &=\ mathrm {(5,76×10^ {−2}\ :L\: mol^ {−1}\ :min^ {−1}) (10\ :min) +\ dfrac {1} {0,200\ :mol^ {−1}}}\\ [4pt]
\ dfrac {1} {[A]} &=\ mathrm {(5,76×10^ {−1}\ :L\: mol^ {−1}) +5,00\ :L\: mol^ {−1}}\ [4pt]
\ dfrac {1} {[A]} &=\ mathrm {5,58\ :L\: mol^ {−1}}\\ [4pt]
[A] &=\ mathrm {1,79×10^ {−1}\ :mol\: L^ {−1}}
\ end {align*}\ nonumber\]
Portanto, 0,179 mol/L de butadieno permanecem no final de 10,0 min, em comparação com os 0,200 mol/L que estavam originalmente presentes.
Se a concentração inicial de butadieno for 0,0200 M, qual é a concentração restante após 20,0 min?
- Resposta
-
0,0196 mol/L
A lei de taxa integrada para nossas reações de segunda ordem tem a forma da equação de uma linha reta:
\ [\ begin {align*}
\ dfrac {1} {[A]} &=kt+\ dfrac {1} {[A] _0}\\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
Um gráfico de\(\dfrac{1}{[A]}\) versus t para uma reação de segunda ordem é uma linha reta com uma inclinação de k e uma interceptação de\(\dfrac{1}{[A]_0}\). Se o gráfico não for uma linha reta, a reação não é de segunda ordem.
Teste os dados fornecidos para mostrar se a dimerização de C 4 H 6 é uma reação de primeira ou segunda ordem.
Solução
| Ensaio | Hora (s) | [C 4 H 6] (M) |
|---|---|---|
| 1 | 0 | 1,00 × 10 −2 |
| 2 | 1600 | 5,04 × 10 −3 |
| 3 | 3200 | 3,37 × 10 −3 |
| 4 | 4800 | 2,53 × 10 −3 |
| 5 | 6200 | 2,08 × 10 −3 |
Para distinguir uma reação de primeira ordem de uma reação de segunda ordem, traçamos ln [C 4 H 6] versus t e comparamos com um gráfico de\(\mathrm{\dfrac{1}{[C_4H_6]}}\) versus t. Os valores necessários para esses gráficos são os seguintes.
| Hora (s) | \(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\) | em [C 4 H 6] |
|---|---|---|
| 0 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">100 | −4,605 |
| 1600 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">198 | −5,289 |
| 3200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">296 | −5,692 |
| 4800 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">395 | −5,978 |
| 6200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">481 | −6,175 |
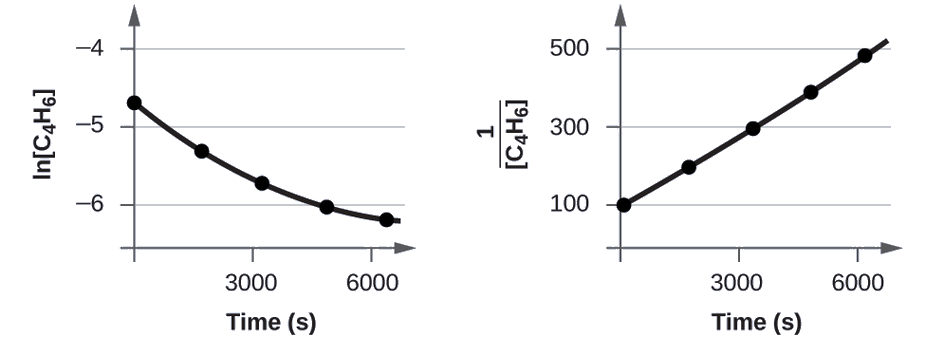
Os gráficos são mostrados na Figura\(\PageIndex{2}\). Como você pode ver, o gráfico de ln [C 4 H 6] versus t não é linear, portanto, a reação não é de primeira ordem. O gráfico de\(\dfrac{1}{[\ce{C4H6}]}\) versus t é linear, indicando que a reação é de segunda ordem.
Os dados a seguir se encaixam em uma lei de taxas de segunda ordem?
| Ensaio | Hora (s) | [A] (M) |
|---|---|---|
| 1 | 5 | 0,952 |
| 2 | 10 | 0,625 |
| 3 | 15 | 0,465 |
| 4 | 20 | 0,370 |
| 5 | 25 | 0,308 |
| 6 | 35 | 0,230 |
- Resposta
-
Sim. O gráfico de\(\dfrac{1}{[A]}\) vs. t é linear:
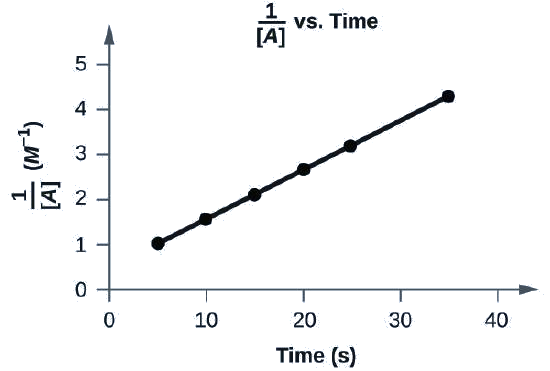
Um gráfico, com o título “1 dividido por [A] versus Tempo” é exibido, com o rótulo “Tempo (s)”, no eixo x. O rótulo “1 dividido por [A]” aparece à esquerda do eixo y. O eixo x mostra marcações começando em zero e continuando em intervalos de 10 até 40, inclusive. O eixo y à esquerda mostra marcações começando em 0 e aumentando em intervalos de 1 até 5, inclusive. Uma linha com tendência crescente é traçada através de seis pontos em aproximadamente (4, 1), (10, 1,5), (15, 2,2), (20, 2,8), (26, 3,4) e (36, 4,4).
Reações de ordem zero
Para reações de ordem zero, a lei da taxa diferencial é:
\[\ce{Rate}=k[A]^0=k \nonumber \]
Uma reação de ordem zero, portanto, exibe uma taxa de reação constante, independentemente da concentração de seus reagentes.
A lei de taxa integrada para uma reação de ordem zero também tem a forma da equação de uma linha reta:
\ [\ begin {align*}
[A] &=−kt+ [A] _0\ label {intzero}\\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
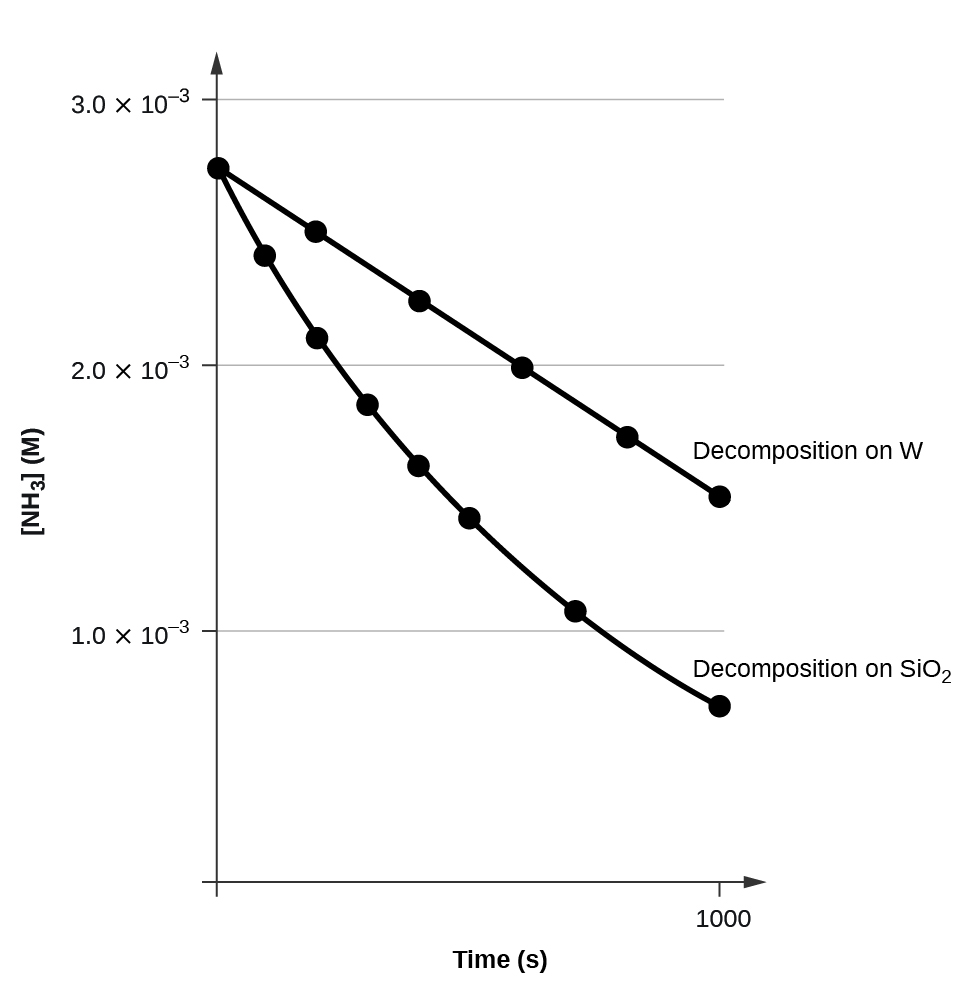
Um gráfico de\([A]\) versus\(t\) para uma reação de ordem zero é uma linha reta com uma inclinação de −k e um intercepto de [A] 0. \(\PageIndex{3}\)A figura mostra um gráfico de [NH 3] versus t para a decomposição da amônia em um fio de tungstênio quente e para a decomposição da amônia em quartzo quente (SiO 2). A decomposição do NH 3 no tungstênio quente é de ordem zero; o gráfico é uma linha reta. A decomposição do NH 3 em quartzo quente não é de ordem zero (é de primeira ordem). A partir da inclinação da linha para a decomposição de ordem zero, podemos determinar a taxa constante:
\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber \]
A meia-vida de uma reação
A meia-vida de uma reação (t 1/2) é o tempo necessário para que metade de uma determinada quantidade de reagente seja consumida. Em cada meia-vida seguinte, metade da concentração restante do reagente é consumida. Usando a decomposição do peróxido de hidrogênio como exemplo, descobrimos que durante a primeira meia-vida (de 0,00 horas para 6,00 horas), a concentração de H 2 O 2 diminui de 1.000 M para 0,500 M. Durante a segunda meia-vida (de 6,00 horas para 12,00 horas), diminui de 0,500 M para 0,250 M; durante a terceira meia-vida, diminui de 0,250 M para 0,125 M. A concentração de H 2 O 2 diminui pela metade durante cada período sucessivo de 6,00 horas. A decomposição do peróxido de hidrogênio é uma reação de primeira ordem e, como pode ser mostrado, a meia-vida de uma reação de primeira ordem é independente da concentração do reagente. No entanto, as meias-vidas das reações com outras ordens dependem das concentrações dos reagentes.
Reações de primeira ordem
Podemos derivar uma equação para determinar a meia-vida de uma reação de primeira ordem a partir da forma alternativa da lei de taxas integradas da seguinte forma:
\ [\ begin {align*}
\ ln\ dfrac {[A] _0} {[A]} &=kt\\ [4pt]
t&=\ ln\ dfrac {[A] _0} {[A]} ×\ dfrac {1} {k}
\ end {align*}\ nonumber\]
Se definirmos o tempo t igual à meia-vida\(t_{1/2}\),, a concentração correspondente de A neste momento é igual a metade de sua concentração inicial. Conseqüentemente, quando\(t=t_{1/2}\),\([A]=\dfrac{1}{2}[A]_0\).
Portanto:
\ [\ begin {align*}
t_ {1/2} &=\ ln\ dfrac {[A] _0} {\ dfrac {1} {2} [A] _0} ×\ dfrac {1} {k}\ [4pt]
&=\ ln 2×\ dfrac {1} {k} =0,693×\ dfrac {1} {k}
\ end {align*}\ nonumber\]
Assim:
\[t_{1/2}=\dfrac{0.693}{k} \nonumber \]
Podemos ver que a meia-vida de uma reação de primeira ordem é inversamente proporcional à constante de taxa k. Uma reação rápida (meia-vida mais curta) terá um k maior; uma reação lenta (meia-vida mais longa) terá um k menor.
Calcule a constante de taxa para a decomposição de primeira ordem do peróxido de hidrogênio em água a 40 °C, usando os dados fornecidos na Figura\(\PageIndex{4}\).
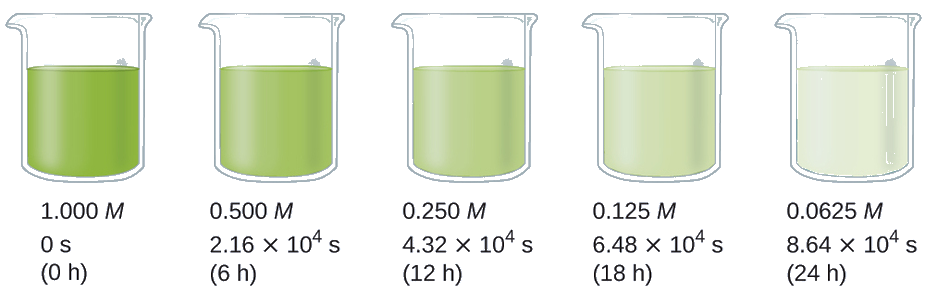
Solução A meia-vida para a decomposição de H 2 O 2 é 2,16 × 10 4 s:
\ [\ begin {align*}
t_ {1/2} &=\ dfrac {0,693} {k}\\ [4pt]
k&=\ dfrac {0,693} {t_ {1/2}} =\ dfrac {0,693} {2,16×10^4\:\ ce s} =3,21×10^ {−5}\:\ ce s^ {−1}
\ end {align*}\ nonumber\]
O decaimento radioativo de primeira ordem do iodo-131 exibe uma taxa constante de 0,138 d −1. Qual é a meia-vida dessa decadência?
- Resposta
-
5,02 d.
Reações de segunda ordem
Podemos derivar a equação para calcular a meia-vida de uma segunda ordem da seguinte forma:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
ou
\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber \]
E se
\[t=t_{1/2} \nonumber \]
depois
\[[A]=\dfrac{1}{2}[A]_0 \nonumber \]
e podemos escrever:
\ dfrac {1} {\ dfrac {1} {2} [A] _0} −\ dfrac {1} {[A] _0} &=kt_ {1/2}\ [4pt]
2 [A] _0−\ dfrac {1} {[A] _0} &=kt_ {1/2}\\ [4pt]]
\ dfrac {1} {[A] _0} &=kt_ {1/2}
\ end {align*}\)
Assim:
\[t_{1/2}=\dfrac{1}{k[A]_0} \nonumber \]
Para uma reação de segunda ordem,\(t_{1/2}\) é inversamente proporcional à concentração do reagente, e a meia-vida aumenta à medida que a reação prossegue porque a concentração do reagente diminui. Consequentemente, descobrimos que o uso do conceito de meia-vida é mais complexo para reações de segunda ordem do que para reações de primeira ordem. Ao contrário das reações de primeira ordem, a constante de taxa de uma reação de segunda ordem não pode ser calculada diretamente a partir da meia-vida, a menos que a concentração inicial seja conhecida.
Reações de ordem zero
Podemos derivar uma equação para calcular a meia-vida de uma reação de ordem zero da seguinte forma:
\[[A]=−kt+[A]_0 \nonumber \]
Quando metade da quantidade inicial de reagente foi consumida\(t=t_{1/2}\)\([A]=\dfrac{[A]_0}{2}\) e. Assim:
\ [\ begin {align*}
\ dfrac {[A] _0} {2} &=−kt_ {1/2} + [A] _0\\ [4pt]
kt_ {1/2} &=\ dfrac {[A] _0} {2}
\ end {align*}\ nonumber\]
e
\[t_{1/2}=\dfrac{[A]_0}{2k} \nonumber \]
A meia-vida de uma reação de ordem zero aumenta à medida que a concentração inicial aumenta. As equações para as leis de taxa diferencial e integrada e as meias-vidas correspondentes para reações de zero, primeira e segunda ordem estão resumidas na Tabela\(\PageIndex{1}\).
| Ordem zero | Primeira ordem | Segunda ordem | |
|---|---|---|---|
| lei tarifária | taxa = k | taxa = k [A] | taxa = k [A] 2 |
| unidades de taxa constante | M é −1 | s −1 | M −1 s −1 |
| lei de taxas integradas | [A] = − kt + [A] 0 | ln [A] = − kt + ln [A] 0 | \(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\) |
| gráfico necessário para ajuste linear de dados de taxa | [A] versus t | ln [A] versus t | \(\dfrac{1}{[A]}\)versus t |
| relação entre a inclinação do gráfico linear e a constante de taxa | k = −inclinação | k = −inclinação | k = +inclinação |
| meia-vida | \(t_{1/2}=\dfrac{[A]_0}{2k}\) | \(t_{1/2}=\dfrac{0.693}{k}\) | \(t_{1/2}=\dfrac{1}{[A]_0k}\) |
Resumo
As leis de taxa diferencial podem ser determinadas pelo método das taxas iniciais ou por outros métodos. Medimos os valores das taxas iniciais de uma reação em diferentes concentrações dos reagentes. A partir dessas medições, determinamos a ordem da reação em cada reagente. As leis de taxas integradas são determinadas pela integração das leis de taxa diferencial correspondentes. As constantes de taxa para essas leis de taxa são determinadas a partir de medições de concentração em vários momentos durante uma reação.
A meia-vida de uma reação é o tempo necessário para diminuir a quantidade de um determinado reagente pela metade. A meia-vida de uma reação de ordem zero diminui à medida que a concentração inicial do reagente na reação diminui. A meia-vida de uma reação de primeira ordem é independente da concentração, e a meia-vida de uma reação de segunda ordem diminui à medida que a concentração aumenta.
Equações-chave
- lei de taxa integrada para reações de ordem zero (Equação\ ref {intzero}):
\([A]=−kt+[A]_0\)com\(t_{1/2}=\dfrac{[A]_0}{2k}\)
- lei de taxa integrada para reações de primeira ordem (Equação\ ref {in1st}):
\(\ln[A]=−kt+ \ln[A]_0\)com\(t_{1/2}=\dfrac{0.693}{k}\)
- lei de taxa integrada para reações de segunda ordem (Equação\ ref {int2nd}):
\(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\)com\(t_{1/2}=\dfrac{1}{[A]_0k}\)
Glossário
- meia-vida de uma reação (t l/2)
- tempo necessário para que metade de uma determinada quantidade de reagente seja consumida
- lei de taxas integradas
- equação que relaciona a concentração de um reagente com o tempo decorrido de reação


