12.3: Leis tarifárias
- Page ID
- 184979
- Explicar a forma e a função de uma lei de taxas
- Use as leis de taxa para calcular as taxas de reação
- Use dados de taxa e concentração para identificar ordens de reação e derivar leis de taxa
Conforme descrito no módulo anterior, a taxa de uma reação é afetada pelas concentrações dos reagentes. As leis de taxa ou equações de taxa são expressões matemáticas que descrevem a relação entre a taxa de uma reação química e a concentração de seus reagentes. Em geral, uma lei de taxas (ou lei de taxa diferencial, como às vezes é chamada) assume a seguinte forma:
\[\ce{rate}=k[A]^m[B]^n[C]^p… \nonumber \]
em que [A], [B] e [C] representam as concentrações molares dos reagentes e k é a constante de taxa, que é específica para uma reação específica a uma determinada temperatura. Os expoentes m, n e p são geralmente números inteiros positivos (embora seja possível que sejam frações ou números negativos). A constante de taxa k e os expoentes m, n e p devem ser determinados experimentalmente observando como a taxa de uma reação muda à medida que as concentrações dos reagentes são alteradas. A constante de taxa k é independente da concentração de A, B ou C, mas varia com a temperatura e a área da superfície.
Os expoentes em uma lei de taxas descrevem os efeitos das concentrações do reagente na taxa de reação e definem a ordem da reação. Considere uma reação para a qual a lei tarifária é:
\[\ce{rate}=k[A]^m[B]^n \nonumber \]
Se o expoente m for 1, a reação é de primeira ordem em relação a A. Se m for 2, a reação é de segunda ordem em relação a A. Se n é 1, a reação é de primeira ordem em B. Se n for 2, a reação é de segunda ordem em B. Se m ou n for zero, a reação é de ordem zero em A ou B, respectivamente, e a taxa da reação não é afetada pela concentração desse reagente. A ordem geral da reação é a soma das ordens em relação a cada reagente. Se m = 1 e n = 1, a ordem geral da reação é de segunda ordem (m + n = 1 + 1 = 2).
A lei tarifária:
\[\ce{rate}=k[\ce{H2O2}] \nonumber \]
descreve uma reação que é de primeira ordem em peróxido de hidrogênio e de primeira ordem em geral. A lei tarifária:
\[\ce{rate}=k[\ce{C4H6}]^2 \nonumber \]
descreve uma reação que é de segunda ordem em C 4 H 6 e de segunda ordem geral. A lei tarifária:
\[\ce{rate}=k[\ce{H+}][\ce{OH-}] \nonumber \]
descreve uma reação que é de primeira ordem em H +, primeira ordem em OH − e segunda ordem geral.
Um experimento mostra que a reação do dióxido de nitrogênio com o monóxido de carbono:
\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \nonumber \]
é de segunda ordem em NO 2 e ordem zero em CO a 100 °C. Qual é a lei de taxa para a reação?
Solução
A reação terá a forma:
\[\ce{rate}=k[\ce{NO2}]^m[\ce{CO}]^n \nonumber \]
A reação é de segunda ordem no NO 2; portanto, m = 2. A reação é de ordem zero em CO; portanto, n = 0. A lei tarifária é:
\[\ce{rate}=k[\ce{NO2}]^2[\ce{CO}]^0=k[\ce{NO2}]^2 \nonumber \]
Lembre-se de que um número elevado à potência zero é igual a 1, portanto [CO] 0 = 1, e é por isso que podemos simplesmente reduzir a concentração de CO da equação da taxa: a taxa de reação depende unicamente da concentração de NO 2. Quando considerarmos os mecanismos de taxa mais adiante neste capítulo, explicaremos como a concentração de um reagente pode não ter efeito sobre uma reação, apesar de estar envolvida na reação.
A lei de taxas para a reação:
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g) \nonumber \]
foi determinado experimentalmente como sendo a taxa = k [NO] 2 [H 2]. Quais são as ordens em relação a cada reagente e qual é a ordem geral da reação?
- Responda
-
- pedido em NO = 2;
- ordem em H 2 = 1;
- ordem geral = 3
Em uma reação de transesterificação, um triglicéride reage com um álcool para formar um éster e glicerol. Muitos estudantes aprendem sobre a reação entre metanol (CH 3 OH) e acetato de etila (CH 3 CH 2 OCOCH 3) como uma reação de amostra antes de estudar as reações químicas que produzem biodiesel:
\[\ce{CH3OH + CH3CH2OCOCH3 ⟶ CH3OCOCH3 + CH3CH2OH} \nonumber \]
A lei de taxa para a reação entre metanol e acetato de etila é, sob certas condições, determinada experimentalmente como sendo:
\[\ce{rate}=k[\ce{CH3OH}] \nonumber \]
Qual é a ordem da reação em relação ao metanol e ao acetato de etila e qual é a ordem geral da reação?
- Responda
-
- ordem em CH 3 OH = 1;
- ordem em CH 3 CH 2 OCOCH 3 = 0;
- ordem geral = 1
Às vezes, é útil usar um método algébrico mais explícito, geralmente chamado de método das taxas iniciais, para determinar as ordens nas leis de taxas. Para usar esse método, selecionamos dois conjuntos de dados de taxa que diferem na concentração de apenas um reagente e configuramos uma proporção entre as duas taxas e as duas leis de taxa. Depois de cancelar termos iguais, ficamos com uma equação que contém apenas uma incógnita, o coeficiente da concentração que varia. Em seguida, resolvemos essa equação para o coeficiente.
O ozônio na alta atmosfera se esgota quando reage com os óxidos de nitrogênio. As taxas das reações dos óxidos de nitrogênio com o ozônio são fatores importantes para decidir o quão significativas essas reações são na formação do buraco de ozônio sobre a Antártica (Figura\(\PageIndex{1}\)). Uma dessas reações é a combinação de óxido nítrico, NO, com ozônio, O 3:
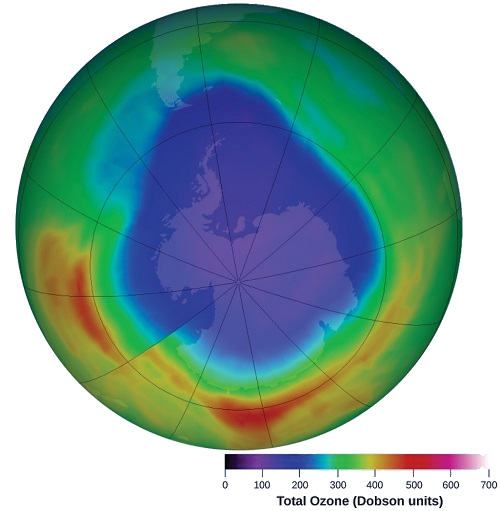
\[\ce{NO}(g)+\ce{O3}(g)⟶\ce{NO2}(g)+\ce{O2}(g) \nonumber \]
Essa reação foi estudada em laboratório e os seguintes dados de taxa foram determinados a 25 °C.
| Ensaio | \([\ce{NO}]\)(mol/L) | \([\ce{O3}]\)(mol/L) | \(\dfrac{Δ[\ce{NO2}]}{Δt}\:\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|---|
| 1 | \ ([\ ce {NO}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">1,00 × 10 −6 | \ ([\ ce {O3}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">3.00 × 10 −6 | \ (\ dfrac {δ [\ ce {NO2}]} {Δt}\:\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; vertical-align:middle; ">6.60 × 10 −5 |
| 2 | \ ([\ ce {NO}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">1,00 × 10 −6 | \ ([\ ce {O3}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">6.00 × 10 −6 | \ (\ dfrac {δ [\ ce {NO2}]} {Δt}\:\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; vertical-align:middle; ">1.32 × 10 −4 |
| 3 | \ ([\ ce {NO}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">1,00 × 10 −6 | \ ([\ ce {O3}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">9.00 × 10 −6 | \ (\ dfrac {δ [\ ce {NO2}]} {Δt}\:\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; vertical-align:middle; ">1.98 × 10 −4 |
| 4 | \ ([\ ce {NO}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">2.00 × 10 −6 | \ ([\ ce {O3}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">9.00 × 10 −6 | \ (\ dfrac {δ [\ ce {NO2}]} {Δt}\:\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; vertical-align:middle; ">3,96 × 10 −4 |
| 5 | \ ([\ ce {NO}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">3,00 × 10 −6 | \ ([\ ce {O3}]\) (mol/L)” style="text-align:center; vertical-align:middle; ">9.00 × 10 −6 | \ (\ dfrac {δ [\ ce {NO2}]} {Δt}\:\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; vertical-align:middle; ">5.94 × 10 −4 |
Determine a lei da taxa e a constante da taxa para a reação a 25 °C.
Solução
A lei tarifária terá o formato:
\[\ce{rate}=k[\ce{NO}]^m[\ce{O3}]^n \nonumber \]
Podemos determinar os valores de m, n e k a partir dos dados experimentais usando o seguinte processo de três partes:
- Determine o valor de m a partir dos dados nos quais [NO] varia e [O 3] é constante. Nos últimos três experimentos, [NO] varia enquanto [O 3] permanece constante. Quando [NÃO] dobra do teste 3 para 4, a taxa dobra, e quando [NÃO] triplica do teste 3 para 5, a taxa também triplica. Assim, a taxa também é diretamente proporcional a [NO], e m na lei da taxa é igual a 1.
- Determine o valor de n a partir de dados nos quais [O 3] varia e [NO] é constante. Nos três primeiros experimentos, [NO] é constante e [O 3] varia. A taxa de reação muda em proporção direta à mudança em [O 3]. Quando [O 3] dobra do teste 1 para 2, a taxa dobra; quando [O 3] triplica do teste 1 para 3, a taxa aumenta também triplica. Assim, a taxa é diretamente proporcional a [O 3] e n é igual a 1. A lei da taxa é, portanto:
\[\ce{rate}=k[\ce{NO}]^1[\ce{O3}]^1=k[\ce{NO}][\ce{O3}] \nonumber \]
- Determine o valor de k a partir de um conjunto de concentrações e a taxa correspondente.
\ [\ begin {align*}
k&=\ mathrm {\ dfrac {rate} {[NO] [O_3]}}\\
&=\ mathrm {\ dfrac {6,60×10^ {−5}\ cancel {mol\: L^ {−1}}\ :s^ {−1}} {(1.00×10^ {−6}\ cancel {mol\) l\: L^ {−1}}) (3,00×10^ {−6}\ :mol\ :L^ {−1})}}\\
&=\ mathrm {2,20×10^7\ :L\ :mol^ {−1}\ :s^ {−1}}
\ end {align*}\ nonumber\]O grande valor de k nos diz que essa é uma reação rápida que pode desempenhar um papel importante na destruição do ozônio se [NO] for grande o suficiente.
O acetaldeído se decompõe quando aquecido para produzir metano e monóxido de carbono de acordo com a equação:
\[\ce{CH3CHO}(g)⟶\ce{CH4}(g)+\ce{CO}(g) \nonumber \]
Determine a lei da taxa e a constante da taxa para a reação a partir dos seguintes dados experimentais:
| Ensaio | \([\ce{CH3CHO}]\)(mol/L) | \(−\dfrac{Δ[\ce{CH3CHO}]}{Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|
| 1 | \ ([\ ce {CH3CHO}]\) (mol/L)” style="text-align:center; ">1,75 × 10 −3 | \ (−\ dfrac {δ [\ ce {CH3CHO}]} {Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">2,06 × 10 −11 |
| 2 | \ ([\ ce {CH3CHO}]\) (mol/L)” style="text-align:center; ">3,50 × 10 −3 | \ (−\ dfrac {δ [\ ce {CH3CHO}]} {Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">8,24 × 10 −11 |
| 3 | \ ([\ ce {CH3CHO}]\) (mol/L)” style="text-align:center; ">7,00 × 10 −3 | \ (−\ dfrac {δ [\ ce {CH3CHO}]} {Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">3,30 × 10 −10 |
- Responda
-
\(\ce{rate}=k[\ce{CH3CHO}]^2\)com k = 6,73 × 10 −6 L/mol/s
Usando o método das taxas iniciais e os dados experimentais, determine a lei da taxa e o valor da constante de taxa para essa reação:
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g) \nonumber \]
| Ensaio | [NÃO] (mol/L) | \([Cl_2]\)(mol/L) | \(−\dfrac{Δ[\ce{NO}]}{2Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|---|
| 1 | 0,10 | \ ([Cl_2]\) (mol/L)” style="text-align:center; ">0.10 | \ (−\ dfrac {δ [\ ce {NO}]} {2Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">0.00300 |
| 2 | 0,10 | \ ([Cl_2]\) (mol/L)” style="text-align:center; ">0.15 | \ (−\ dfrac {δ [\ ce {NO}]} {2Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">0.00450 |
| 3 | 0,15 | \ ([Cl_2]\) (mol/L)” style="text-align:center; ">0.10 | \ (−\ dfrac {δ [\ ce {NO}]} {2Δt}\ mathrm {(mol\ :L^ {−1}\ :s^ {−1})}\)” style="text-align:center; ">0.00675 |
Solução
A lei de taxas para essa reação terá a forma:
\[\ce{rate}=k[\ce{NO}]^m[\ce{Cl2}]^n \nonumber \]
Como no exemplo\(\PageIndex{2}\), podemos abordar esse problema de forma gradual, determinando os valores de m e n a partir dos dados experimentais e, em seguida, usando esses valores para determinar o valor de k. Neste exemplo, no entanto, usaremos uma abordagem diferente para determinar os valores de m e n:
Determine o valor de m a partir dos dados em que [NO] varia e [Cl 2] é constante. Podemos escrever as proporções com os subscritos x e y para indicar dados de dois ensaios diferentes:
\[\dfrac{\ce{rate}_x}{\ce{rate}_y}=\dfrac{k[\ce{NO}]^m_x[\ce{Cl2}]^n_x}{k[\ce{NO}]^m_y[\ce{Cl2}]^n_y} \nonumber \]
Usar a terceira e a primeira tentativa, na qual [Cl 2] não varia, dá:
\[\mathrm{\dfrac{rate\: 3}{rate\: 1}}=\dfrac{0.00675}{0.00300}=\dfrac{k(0.15)^m(0.10)^n}{k(0.10)^m(0.10)^n} \nonumber \]
Depois de cancelar termos equivalentes no numerador e no denominador, ficamos com:
\[\dfrac{0.00675}{0.00300}=\dfrac{(0.15)^m}{(0.10)^m} \nonumber \]o que simplifica para:
\[2.25=(1.5)^m \nonumber \]
Podemos usar registros naturais para determinar o valor do expoente m:
\ ln (2,25) &=m\ ln (1,5)
\ dfrac {\ ln (2,25)} {\ ln (1,5)} &=m
2&=m
\ end {align*}\)
Podemos confirmar o resultado facilmente, pois:
- Determine o valor de n a partir de dados nos quais [Cl 2] varia e [NO] é constante. \[\mathrm{\dfrac{rate\: 2}{rate\: 1}}=\dfrac{0.00450}{0.00300}=\dfrac{k(0.10)^m(0.15)^n}{k(0.10)^m(0.10)^n} \nonumber \]
O cancelamento dá:
\[\dfrac{0.0045}{0.0030}=\dfrac{(0.15)^n}{(0.10)^n} \nonumber \]
o que simplifica para:
\[1.5=(1.5)^n \nonumber \]
Assim, n deve ser 1, e a forma da lei de taxas é:
\[\ce{Rate}=k[\ce{NO}]^m[\ce{Cl2}]^n=k[\ce{NO}]^2[\ce{Cl2}] \nonumber \]
- Determine o valor numérico da constante de taxa k com as unidades apropriadas. As unidades para a taxa de uma reação são mol/L/s. As unidades para k são o que for necessário para que a substituição na expressão da lei de taxa forneça as unidades apropriadas para a taxa. Neste exemplo, as unidades de concentração são mol 3 /L 3. As unidades para k devem ser mol −2 L 2 /s para que a taxa seja em termos de mol/L/s.
Para determinar o valor de k uma vez que a expressão da lei de taxas tenha sido resolvida, basta inserir os valores da primeira tentativa experimental e resolver k:
\ (\ begin {align*}
\ mathrm {0.00300\ :mol\ :L^ {−1}\ :s^ {−1}} &=k\ mathrm {(0,10\ :mol\ :L^ {−1}) ^2 (0,10\ :mol\ :L^ {−1}) ^1}\\ k&=\ molm {3.0\ :L^ {−1}) ^1}\\
k&=\ molm {3,0\ ::^ {−2}\ :L^2\ :s^ {−1}}
\ end {align*}\)
Use os dados de taxa inicial fornecidos para derivar a lei da taxa para a reação cuja equação é:
\[\ce{OCl-}(aq)+\ce{I-}(aq)⟶\ce{OI-}(aq)+\ce{Cl-}(aq) \nonumber \]
| Ensaio | [OCl −] (mol/L) | [I −] (mol/L) | Taxa inicial (mol/L/s) |
|---|---|---|---|
| 1 | 0,0040 | 0,0020 | 0,00184 |
| 2 | 0,0020 | 0,0040 | 0,00092 |
| 3 | 0,0020 | 0,0020 | 0,00046 |
Determine a expressão da lei de taxa e o valor da constante de taxa k com unidades apropriadas para essa reação.
- Responda
-
\(\mathrm{\dfrac{rate\: 2}{rate\: 3}}=\dfrac{0.00092}{0.00046}=\dfrac{k(0.0020)^x(0.0040)^y}{k(0.0020)^x(0.0020)^y}\)
2,00 = 2,00 y
y = 1
\(\mathrm{\dfrac{rate\: 1}{rate\: 2}}=\dfrac{0.00184}{0.00092}=\dfrac{k(0.0040)^x(0.0020)^y}{k(0.0020)^x(0.0040)^y}\)
\ (\ begin {align*}
2.00&=\ dfrac {2^x} {2^y}\\
2.00&=\ dfrac {2^x} {2^1}\\
4.00&=2^x\\
x&=2
\ end {align*}\)
Substituindo os dados de concentração do ensaio 1 e resolvendo k, obtém-se:
\ (\ begin {align*}
\ ce {taxa} &=k [\ ce {OCl-}] ^2 [\ ce {I-}] ^1\\
0.00184&=k (0,0040) ^2 (0,0020) ^1\\
k&=\ mathrm {5,75×10^4\ :mol^ {−2}\ :L^2\ :s^ {−1}
\ end {align*}\)
Unidades constantes de ordem de reação e taxa
Em alguns de nossos exemplos, as ordens de reação na lei de taxas são as mesmas que os coeficientes na equação química da reação. Isso é apenas uma coincidência e muitas vezes não é o caso. As leis de taxa podem exibir ordens fracionárias para alguns reagentes, e ordens de reação negativas às vezes são observadas quando um aumento na concentração de um reagente causa uma diminuição na taxa de reação. Alguns exemplos que ilustram esses pontos são fornecidos:
\ (\ ce {NO2 + CONO + CO2}\ hspace {20px}\ ce {taxa} =k [\ ce {NO2}] ^2\\
\ ce {CH3CHOCH4 + CO}\ hspace {20px}\ ce {taxa} =k [\ ce {CH3CHO}] ^2\
\\ ce {2N2O52NO2 + O2}\ hspace {20px}\ ce {taxa} =k [\ ce {N2O5}]\
\ ce {2NO2 + F22NO2F}\ hspace {20px}\ ce {taxa} =k [\ ce {NO2}] [\ ce {F2}]\\
\ ce {2 No2Cl2NO2 + Cl2}\ hspace {20px}\ ce {taxa} =k [\ ce {No2Cl}]\)
É importante observar que as leis de taxa são determinadas apenas por experimentos e não são previstas de forma confiável pela estequiometria de reação.
As ordens de reação também desempenham um papel na determinação das unidades para a constante de taxa k. No exemplo\(\PageIndex{2}\), uma reação de segunda ordem, descobrimos que as unidades para k são\(\mathrm{L\:mol^{-1}\:s^{-1}}\), enquanto em Example\(\PageIndex{3}\), uma reação de terceira ordem, descobrimos que as unidades para k são mol −2 L 2 /s. De um modo mais geral, as unidades para a constante de taxa para a reação de ordem\( (m+n)\) são\(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\). A tabela\(\PageIndex{1}\) resume as unidades de taxa constante para ordens de reação comuns.
| Ordem de reação | Unidades de k |
|---|---|
| \( (m+n)\) | \(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\) |
| zero | mol/L/s |
| primeiro | s −1 |
| segundo | L/mol/s |
| terceiro | mol −2 L 2 s −1 |
Observe que as unidades na tabela também podem ser expressas em termos de molaridade (M) em vez de mol/L. Além disso, unidades de tempo diferentes da segunda (como minutos, horas, dias) podem ser usadas, dependendo da situação.
Resumo
As leis de taxas fornecem uma descrição matemática de como as mudanças na quantidade de uma substância afetam a taxa de uma reação química. As leis de taxas são determinadas experimentalmente e não podem ser previstas pela estequiometria de reação. A ordem da reação descreve o quanto uma mudança na quantidade de cada substância afeta a taxa geral, e a ordem geral de uma reação é a soma das ordens de cada substância presente na reação. As ordens de reação são normalmente de primeira ordem, segunda ordem ou ordem zero, mas ordens fracionárias e até negativas são possíveis.
Glossário
- método de taxas iniciais
- uso de um método algébrico mais explícito para determinar as ordens em uma lei de taxas
- ordem geral de reação
- soma das ordens de reação para cada substância representada na lei de taxas
- constante de taxa (k)
- constante de proporcionalidade na relação entre a taxa de reação e as concentrações de reagentes
- lei tarifária
- (também, equação de taxa) equação matemática que mostra a dependência da taxa de reação na constante de taxa e na concentração de um ou mais reagentes
- ordem de reação
- valor de um expoente em uma lei de taxas, expresso como um número ordinal (por exemplo, ordem zero para 0, primeira ordem para 1, segunda ordem para 2 e assim por diante)


