Skip to main content
Global

12.1: Taxas de reação química

  1. Last updated
  2. Save as PDF
  • Page ID
    184959

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de
    • Defina a taxa de reação química
    • Derive expressões de taxa da equação balanceada para uma determinada reação química
    • Calcule taxas de reação a partir de dados

    Uma taxa é uma medida de como algumas propriedades variam com o tempo. A velocidade é uma taxa familiar que expressa a distância percorrida por um objeto em um determinado período de tempo. O salário é uma taxa que representa a quantidade de dinheiro ganha por uma pessoa que trabalha por um determinado período de tempo. Da mesma forma, a taxa de uma reação química é uma medida de quanto reagente é consumido, ou quanto produto é produzido, pela reação em um determinado período de tempo.

    A taxa de reação é a mudança na quantidade de um reagente ou produto por unidade de tempo. As taxas de reação são, portanto, determinadas medindo a dependência temporal de alguma propriedade que pode estar relacionada às quantidades de reagentes ou produtos. As taxas de reações que consomem ou produzem substâncias gasosas, por exemplo, são convenientemente determinadas pela medição de mudanças no volume ou na pressão. Para reações envolvendo uma ou mais substâncias coloridas, as taxas podem ser monitoradas por meio de medições de absorção de luz. Para reações envolvendo eletrólitos aquosos, as taxas podem ser medidas por meio de mudanças na condutividade de uma solução.

    Para reagentes e produtos em solução, suas quantidades relativas (concentrações) são convenientemente usadas para fins de expressão de taxas de reação. Se medirmos a concentração de peróxido de hidrogênio, H 2 O 2, em uma solução aquosa, descobrimos que ela muda lentamente ao longo do tempo à medida que o H 2 O 2 se decompõe, de acordo com a equação:

    \[\ce{2H2O2}(aq)⟶\ce{2H2O}(l)+\ce{O2}(g) \nonumber \]

    A taxa na qual o peróxido de hidrogênio se decompõe pode ser expressa em termos da taxa de variação de sua concentração, conforme mostrado aqui:

    \ [\ begin {align*}
    \ ce {taxa\: de\: decomposição\: de\: H_2O_2}
    &=\ mathrm {−\ dfrac {mudança\: em\: concentração\: de\: reagente} {tempo\: intervalo}}\\ [4pt]
    &=−\ dfrac {[\ ce {H2O2}] _ {t_t_4pt] 2} − [\ ce {H2O2}] _ {t_1}} {t_2−t_1}\\ [4pt]
    &=−\ dfrac {δ [\ ce {H2O2}]} {Δt}
    \ end {align*}\ nonumber\]

    Essa representação matemática da mudança na concentração das espécies ao longo do tempo é a expressão da taxa para a reação. Os colchetes indicam concentrações molares e o símbolo delta (Δ) indica “mudança”. Assim,\([\ce{H2O2}]_{t_1}\) representa a concentração molar de peróxido de hidrogênio em algum momento t 1; da mesma forma,\([\ce{H2O2}]_{t_2}\) representa a concentração molar de peróxido de hidrogênio em um momento posterior t 2; e Δ[ H 2 O 2] representa a mudança em concentração molar de peróxido de hidrogênio durante o intervalo de tempo Δt (ou seja, t 2 − t 1). Como a concentração do reagente diminui à medida que a reação prossegue, Δ[ H 2 O 2] é uma quantidade negativa; colocamos um sinal negativo na frente da expressão porque as taxas de reação são, por convenção, quantidades positivas. \(\PageIndex{1}\)A figura fornece um exemplo de dados coletados durante a decomposição de H 2 O 2.

    alt
    Figura\(\PageIndex{1}\): A taxa de decomposição de H 2 O 2 em uma solução aquosa diminui à medida que a concentração de H 2 O 2 diminui.

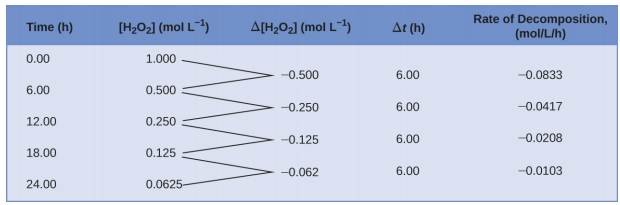
    Para obter os resultados tabulados dessa decomposição, a concentração de peróxido de hidrogênio foi medida a cada 6 horas ao longo de um dia a uma temperatura constante de 40 °C. As taxas de reação foram calculadas para cada intervalo de tempo dividindo a mudança na concentração pelo incremento de tempo correspondente, como mostrado aqui durante o primeiro período de 6 horas:

    \[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.500\: mol/L−1.000\: mol/L)}{(6.00\: h−0.00\: h)}=0.0833\: mol\:L^{−1}\:h^{−1}} \nonumber \]

    Observe que as taxas de reação variam com o tempo, diminuindo à medida que a reação prossegue. Os resultados do último período de 6 horas geram uma taxa de reação de:

    \[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.0625\:mol/L−0.125\:mol/L)}{(24.00\:h−18.00\:h)}=0.0104\:mol\:L^{−1}\:h^{−1}} \nonumber \]

    Esse comportamento indica que a reação diminui continuamente com o tempo. Usar as concentrações no início e no final de um período de tempo durante o qual a taxa de reação está mudando resulta no cálculo de uma taxa média para a reação nesse intervalo de tempo. Em qualquer momento específico, a taxa na qual uma reação está ocorrendo é conhecida como sua taxa instantânea. A taxa instantânea de uma reação no “tempo zero”, quando a reação começa, é sua taxa inicial. Considere a analogia de um carro desacelerando ao se aproximar de um sinal de parada. A taxa inicial do veículo - análoga ao início de uma reação química - seria a leitura do velocímetro no momento em que o motorista começa a pressionar os freios (t 0). Alguns momentos depois, a taxa instantânea em um momento específico - chame-a de t 1 - seria um pouco mais lenta, conforme indicado pela leitura do velocímetro naquele momento. Com o passar do tempo, a taxa instantânea continuará caindo até chegar a zero, quando o carro (ou reação) parar. Ao contrário da velocidade instantânea, a velocidade média do carro não é indicada pelo velocímetro; mas pode ser calculada como a razão entre a distância percorrida e o tempo necessário para parar completamente o veículo (Δt). Como o carro em desaceleração, a taxa média de uma reação química cairá em algum lugar entre suas taxas inicial e final.

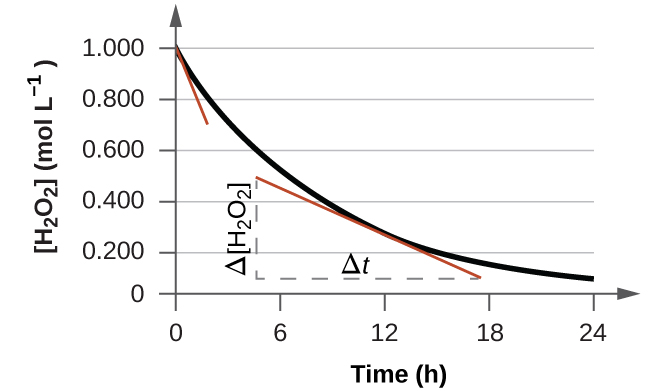
    A taxa instantânea de uma reação pode ser determinada de duas maneiras. Se as condições experimentais permitirem a medição das mudanças de concentração em intervalos de tempo muito curtos, as taxas médias calculadas conforme descrito anteriormente fornecem aproximações razoavelmente boas das taxas instantâneas. Alternativamente, um procedimento gráfico pode ser usado que, de fato, produza os resultados que seriam obtidos se medições de curto intervalo de tempo fossem possíveis. Se representarmos graficamente a concentração de peróxido de hidrogênio em relação ao tempo, a taxa instantânea de decomposição de H 2 O 2 a qualquer momento t é dada pela inclinação de uma linha reta tangente à curva naquele momento (Figura\(\PageIndex{2}\)). Podemos usar o cálculo para avaliar as inclinações dessas retas tangentes, mas o procedimento para fazer isso está além do escopo deste capítulo.

    alt
    Figura\(\PageIndex{1}\): Este gráfico mostra um gráfico da concentração versus tempo para uma solução de 1.000 M de H 2 O 2. A taxa em qualquer instante é igual ao oposto da inclinação de uma reta tangencial a essa curva naquele momento. As tangentes são mostradas em t = 0 h (“taxa inicial”) e em t = 10 h (“taxa instantânea” naquele momento específico).
    Taxas de reação na análise: tiras de teste para análise de urina

    Os médicos costumam usar tiras de teste descartáveis para medir as quantidades de várias substâncias na urina de um paciente (Figura\(\PageIndex{2}\)). Essas tiras de teste contêm vários reagentes químicos, embutidos em pequenas almofadas em vários locais ao longo da faixa, que sofrem alterações de cor quando expostas a concentrações suficientes de substâncias específicas. As instruções de uso das tiras de teste geralmente enfatizam que o tempo de leitura adequado é fundamental para obter os melhores resultados. Essa ênfase no tempo de leitura sugere que os aspectos cinéticos das reações químicas que ocorrem na tira de teste são considerações importantes.

    O teste de glicose urinária se baseia em um processo de duas etapas representado pelas equações químicas mostradas aqui:

    \[\ce{C6H12O6 + O2}\underset{\large\textrm{catalyst}}{\xrightarrow{\hspace{45px}}}\ce{C6H10O6 + H2O2} \label{eq1} \]

    \[\ce{2H2O2 + 2I-}\underset{\large\textrm{catalyst}}{\xrightarrow{\hspace{45px}}}\ce{I2 + 2H2O + O2} \label{eq2} \]

    A equação\(\ref{eq1}\) mostra a oxidação da glicose na urina para produzir glucolactona e peróxido de hidrogênio. O peróxido de hidrogênio produzido posteriormente oxida o íon iodeto incolor para produzir iodo marrom (Equação\(\ref{eq2}\)), que pode ser detectado visualmente. Algumas tiras incluem uma substância adicional que reage com o iodo para produzir uma mudança de cor mais distinta.

    As duas reações de teste mostradas acima são inerentemente muito lentas, mas suas taxas são aumentadas por enzimas especiais incorporadas na almofada de teste. Este é um exemplo de catálise, um tópico discutido posteriormente neste capítulo. Uma tira de teste de glicose típica para uso com urina requer aproximadamente 30 segundos para completar as reações de formação de cor. Ler o resultado muito cedo pode levar a concluir que a concentração de glicose na amostra de urina é menor do que realmente é (um resultado falso-negativo). Esperar muito tempo para avaliar a mudança de cor pode levar a um falso positivo devido à oxidação mais lenta (não catalisada) do íon iodeto por outras substâncias encontradas na urina.

    alt
    Figura\(\PageIndex{2}\): As tiras de teste são comumente usadas para detectar a presença de substâncias específicas na urina de uma pessoa. Muitas tiras de teste têm várias almofadas contendo vários reagentes para permitir a detecção de várias substâncias em uma única tira. (crédito: Iqbal Osman).

    Taxas relativas de reação

    A taxa de uma reação pode ser expressa em termos da mudança na quantidade de qualquer reagente ou produto e pode ser simplesmente derivada da estequiometria da reação. Considere a reação representada pela seguinte equação:

    \[\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g) \nonumber \]

    Os fatores estequiométricos derivados dessa equação podem ser usados para relacionar as taxas de reação da mesma maneira que são usados com quantidades relacionadas de reagentes e produtos. A relação entre as taxas de reação expressas em termos de produção de nitrogênio e consumo de amônia, por exemplo, é:

    \[\mathrm{−\dfrac{Δmol\: NH_3}{Δ\mathit t}×\dfrac{1\: mol\: N_2}{2\: mol\: NH_3}=\dfrac{Δmol\:N_2}{Δ\mathit t}} \nonumber \]

    Podemos expressar isso de forma mais simples sem mostrar as unidades do fator estequiométrico:

    \[−\dfrac{1}{2}\dfrac{\mathrm{Δmol\:NH_3}}{Δt}=\dfrac{\mathrm{Δmol\:N_2}}{Δt} \nonumber \]

    Observe que um sinal negativo foi adicionado para explicar os sinais opostos das duas mudanças de quantidade (a quantidade de reagente está diminuindo enquanto a quantidade do produto está aumentando). Se os reagentes e produtos estiverem presentes na mesma solução, as quantidades molares podem ser substituídas por concentrações:

    \[−\dfrac{1}{2}\dfrac{Δ[\ce{NH3}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt} \nonumber \]

    Da mesma forma, a taxa de formação de H 2 é três vezes a taxa de formação de N 2 porque três moles de H 2 se formam durante o tempo necessário para a formação de um mol de N 2:

    \[\dfrac{1}{3}\dfrac{Δ[\ce{H2}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt} \nonumber \]

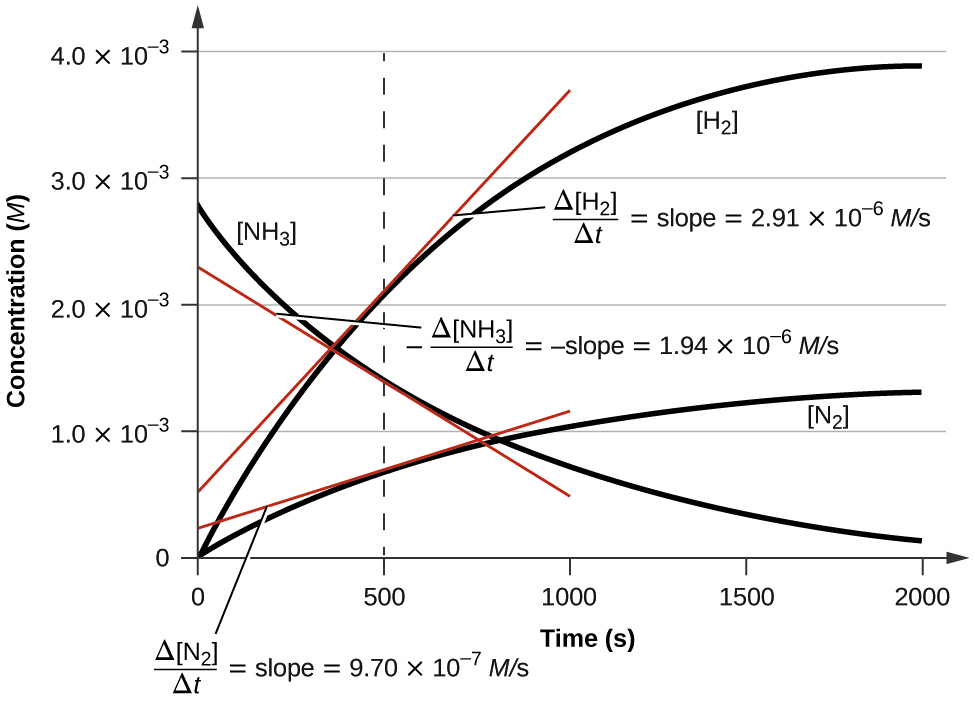
    A figura\(\PageIndex{3}\) ilustra a mudança nas concentrações ao longo do tempo para a decomposição de amônia em nitrogênio e hidrogênio a 1100 °C. Podemos ver pelas inclinações das tangentes desenhadas em t = 500 segundos que as taxas instantâneas de mudança nas concentrações dos reagentes e produtos estão relacionados por seus fatores estequiométricos. Observa-se que a taxa de produção de hidrogênio, por exemplo, é três vezes maior do que a da produção de nitrogênio:

    \[\dfrac{2.91×10^{−6}\:M/\ce s}{9.71×10^{−6}\:M/\ce s}≈3 \nonumber \]

    alt
    Figura\(\PageIndex{3}\): Este gráfico mostra as mudanças nas concentrações dos reagentes e produtos durante a reação \(\ce{2NH3⟶N2 + 3H2}\). As taxas de variação das três concentrações estão relacionadas por seus fatores estequiométricos, conforme mostrado pelas diferentes inclinações das tangentes em t = 500 s.
    Exemplo\(\PageIndex{1}\): Expressions for Relative Reaction Rates

    O primeiro passo na produção de ácido nítrico é a combustão da amônia:

    \[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g) \nonumber \]

    Escreva as equações que relacionam as taxas de consumo dos reagentes e as taxas de formação dos produtos.

    Solução

    Considerando a estequiometria dessa reação homogênea, as taxas de consumo de reagentes e formação de produtos são:

    \[−\dfrac{1}{4}\dfrac{Δ[\ce{NH3}]}{Δt}=−\dfrac{1}{5}\dfrac{Δ[\ce{O2}]}{Δt}=\dfrac{1}{4}\dfrac{Δ[\ce{NO}]}{Δt}=\dfrac{1}{6}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber \]

    Exercício\(\PageIndex{1}\)

    A taxa de formação de Br 2 é 6,0 × 10 −6 mol/L/s em uma reação descrita pela seguinte equação iônica líquida:

    \[\ce{5Br- + BrO3- + 6H+ ⟶ 3Br2 + 3H2O} \nonumber \]

    Escreva as equações que relacionam as taxas de consumo dos reagentes e as taxas de formação dos produtos.

    Responda

    \[−\dfrac{1}{5}\dfrac{Δ[\ce{Br-}]}{Δt}=−\dfrac{Δ[\ce{BrO3-}]}{Δt}=−\dfrac{1}{6}\dfrac{Δ[\ce{H+}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{Br2}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber \]

    Exemplo\(\PageIndex{2}\): Reaction Rate Expressions for Decomposition of H2O2

    O gráfico na Figura\(\PageIndex{3}\) mostra a taxa de decomposição de H 2 O 2 ao longo do tempo:

    \[\ce{2H2O2 ⟶ 2H2O + O2} \nonumber \]

    Com base nesses dados, a taxa instantânea de decomposição de H 2 O 2 em t = 11,1 h é determinada como 3,20 × 10 −2 mol/L/h, ou seja:

    \[−\dfrac{Δ[\ce{H2O2}]}{Δt}=\mathrm{3.20×10^{−2}\:mol\: L^{−1}\:h^{−1}} \nonumber \]

    Qual é a taxa instantânea de produção de H 2 O e O 2?

    Solução

    Usando a estequiometria da reação, podemos determinar que:

    \[−\dfrac{1}{2}\dfrac{Δ[\ce{H2O2}]}{Δt}=\dfrac{1}{2}\dfrac{Δ[\ce{H2O}]}{Δt}=\dfrac{Δ[\ce{O2}]}{Δt} \nonumber \]

    Portanto:

    \[\mathrm{\dfrac{1}{2}×3.20×10^{−2}\:mol\:L^{−1}\:h^{−1}}=\dfrac{Δ[\ce{O2}]}{Δt} \nonumber \]

    e

    \[\dfrac{Δ[\ce{O2}]}{Δt}=\mathrm{1.60×10^{−2}\:mol\:L^{−1}\:h^{−1}} \nonumber \]

    Exercício\(\PageIndex{2}\)

    Se a taxa de decomposição da amônia, NH 3, a 1150 K é 2,10 × 10 −6 mol/L/s, qual é a taxa de produção de nitrogênio e hidrogênio?

    Responda

    1,05 × 10 −6 mol/L/s, N 2 e 3,15 × 10 −6 mol/L/s, H 2.

    Resumo

    A taxa de uma reação pode ser expressa em termos da diminuição da quantidade de um reagente ou do aumento na quantidade de um produto por unidade de tempo. As relações entre diferentes expressões de taxa para uma determinada reação são derivadas diretamente dos coeficientes estequiométricos da equação que representa a reação.

    Glossário

    taxa média
    taxa de uma reação química calculada como a razão entre uma mudança medida na quantidade ou concentração da substância e o intervalo de tempo durante o qual a mudança ocorreu
    taxa inicial
    taxa instantânea de uma reação química em t = 0 s (imediatamente após o início da reação)
    taxa instantânea
    taxa de uma reação química em qualquer instante no tempo, determinada pela inclinação da linha tangencial a um gráfico de concentração em função do tempo
    taxa de reação
    medida da velocidade com que ocorre uma reação química
    expressão de taxa
    representação matemática relacionando a taxa de reação a mudanças na quantidade, concentração ou pressão de espécies de reagentes ou produtos por unidade de tempo