9.E: Gases (exercícios)

Last updated
Save as PDF

Page ID: 185419

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

9.1: Pressão do gás

Q9.1.1

Por que facas afiadas são mais eficazes do que facas sem brilho (Dica: pense na definição de pressão)?

S9.1.1

A aresta cortante de uma faca que foi afiada tem uma área de superfície menor do que uma faca cega. Como a pressão é a força por unidade de área, uma faca afiada exercerá uma pressão mais alta com a mesma quantidade de força e cortará o material com mais eficiência.

Q9.1.2

Por que algumas pontes pequenas têm limites de peso que dependem de quantas rodas ou eixos o veículo de travessia tem?

Q9.1.3

Por que você deveria rolar ou engatinhar de barriga em vez de caminhar por um lago bem congelado?

S9.1.3

Deitar distribui seu peso por uma área de superfície maior, exercendo menos pressão sobre o gelo do que em pé. Se você exercer menos pressão, é menos provável que rompa gelo fino.

Q9.1.4

Uma pressão barométrica típica em Redding, Califórnia, é de cerca de 750 mm Hg. Calcule essa pressão em atm e kPa.

Q9.1.5

Uma pressão barométrica típica em Denver, Colorado, é de 615 mm Hg. O que é essa pressão em atmosferas e quilopascais?

S 9.1.5

0,809 atm; 82,0 kPa

Q9.1.6

Uma pressão barométrica típica em Kansas City é de 740 torr. O que é essa pressão nas atmosferas, em milímetros de mercúrio e em quilopascais?

Q9.1.7

Os medidores de pressão de pneus canadenses são marcados em unidades de quilopascais. Qual leitura nesse medidor corresponde a 32 psi?

S 9.1.7

2,2 × 10 ² kPa

Q9.1.8

Durante os pousos dos Viking em Marte, a pressão atmosférica foi determinada em média em torno de 6,50 milibares (1 bar = 0,987 atm). Qual é essa pressão em torr e kPa?

Q9.1.9

A pressão da atmosfera na superfície do planeta Vênus é de cerca de 88,8 atm. Compare essa pressão em psi com a pressão normal na Terra ao nível do mar em psi.

S9.1.9

Terra: 14,7 lb em ^—2; Vênus: 13,1 × 10 ³ lb em ⁻²

Q9.1.10

Um catálogo de laboratório médico descreve a pressão em um cilindro de gás como 14,82 MPa. Qual é a pressão desse gás nas atmosferas e no torr?

Q9.1.11

Considere esse cenário e responda às seguintes perguntas: Em um dia de meados de agosto no nordeste dos Estados Unidos, as seguintes informações foram publicadas no jornal local: pressão atmosférica ao nível do mar 29,97 pol., 1013,9 mbar.

Qual foi a pressão em kPa?
A pressão perto do litoral no nordeste dos Estados Unidos geralmente é relatada perto de 30,0 pol. Abraço. Durante um furacão, a pressão pode cair para cerca de 28,0 pol. Abraço. Calcule a queda na pressão em torr.

S9.1.11

(a) 101,5 kPa; (b) Queda de 51 torr

Q9.1.12

Por que é necessário usar um líquido não volátil em um barômetro ou manômetro?

Q9.1.13

A pressão de uma amostra de gás é medida ao nível do mar com um manômetro de extremidade fechada. O líquido no manômetro é mercúrio. Determine a pressão do gás em:

rasgar
Pa
barra

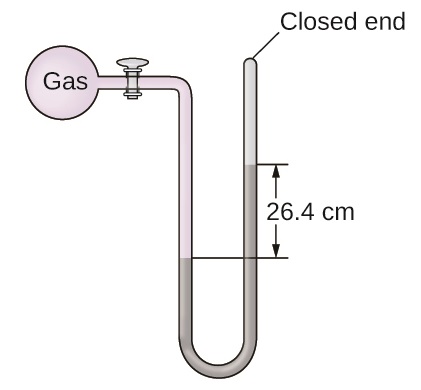
S9.1.13

(a) 264 torr; (b) 35.200 Pa; (c) 0,352 bar

Q9.1.14

A pressão de uma amostra de gás é medida com um manômetro de extremidade aberta, parcialmente mostrado à direita. O líquido no manômetro é mercúrio. Supondo que a pressão atmosférica seja de 29,92 pol. Hg, determine a pressão do gás em:

rasgar
Pa
barra

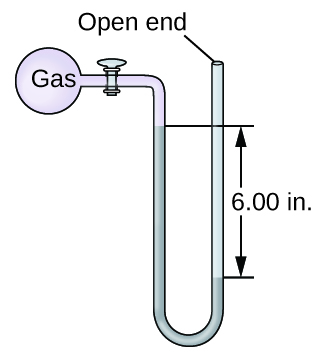
Q9.1.15

A pressão de uma amostra de gás é medida ao nível do mar com um manômetro de mercúrio de extremidade aberta. Supondo que a pressão atmosférica seja 760,0 mm Hg, determine a pressão do gás em:

mm Hg
caixa eletrônico
KPa

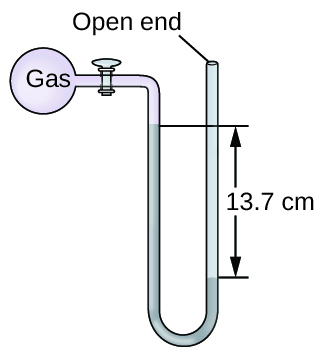
S 9.1.15

(a) 623 mm Hg; (b) 0,820 atm; (c) 83,1 kPa

Q9.1.16

A pressão de uma amostra de gás é medida ao nível do mar com um manômetro de mercúrio de extremidade aberta. Supondo que a pressão atmosférica seja de 760 mm Hg, determine a pressão do gás em:

mm Hg
caixa eletrônico
KPa

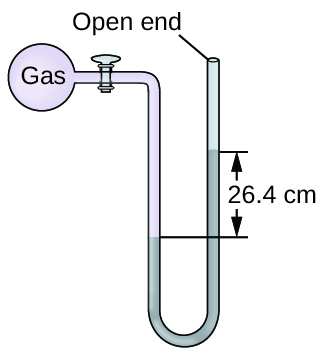
Q9.1.17

Como o uso de um líquido volátil afetaria a medição de um gás usando manômetros abertos versus manômetros de extremidade fechada?

S9.1.17

Com um manômetro de extremidade fechada, nenhuma alteração seria observada, pois o líquido vaporizado contribuiria com pressões iguais e opostas em ambos os braços do tubo do manômetro. No entanto, com um manômetro de extremidade aberta, uma leitura de pressão mais alta do gás seria obtida do que o esperado, uma vez que P _gas = P _atm + P _{vol líquido}.

9.2: Relacionando pressão, volume, quantidade e temperatura: a lei do gás ideal

Q9.2.1

Às vezes, deixar uma bicicleta ao sol em um dia quente pode causar uma explosão. Por quê?

Q9.2.2

Explique como o volume das bolhas esgotadas por um mergulhador (Figura) muda à medida que elas sobem à superfície, supondo que permaneçam intactas.

S9.2.2

Conforme as bolhas sobem, a pressão diminui, então seu volume aumenta conforme sugerido pela lei de Boyle.

Q9.2.3

Uma forma de afirmar a lei de Boyle é “Todas as outras coisas sendo iguais, a pressão de um gás é inversamente proporcional ao seu volume”. (a) Qual é o significado do termo “inversamente proporcional”? (b) Quais são as “outras coisas” que devem ser iguais?

Q9.2.4

Uma forma alternativa de afirmar a lei de Avogadro é “Todas as outras coisas sendo iguais, o número de moléculas em um gás é diretamente proporcional ao volume do gás”.

Qual é o significado do termo “diretamente proporcional”?
Quais são as “outras coisas” que devem ser iguais?

9.2.4

(a) O número de partículas no gás aumenta à medida que o volume aumenta. (b) temperatura, pressão

Q9.2.5

Como o gráfico na Figura mudaria se o número de moles de gás na amostra usada para determinar a curva fosse dobrado?

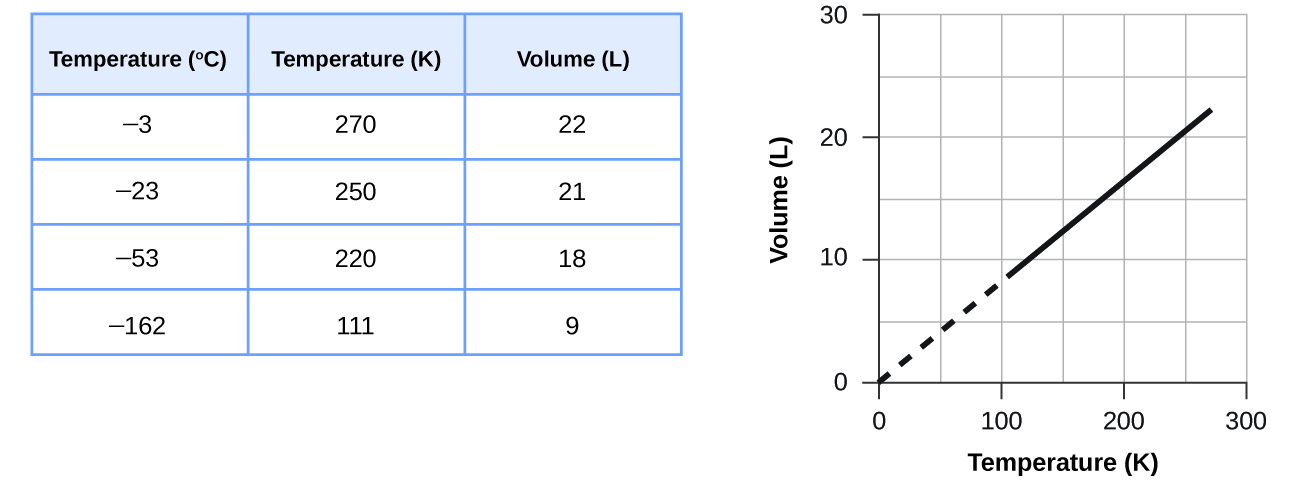
O volume e a temperatura estão linearmente relacionados para 1 mol de gás metano a uma pressão constante de 1 atm. Se a temperatura estiver em kelvin, o volume e a temperatura são diretamente proporcionais. A linha para em 111 K porque o metano se liquefaz nessa temperatura; quando extrapolado, ele cruza a origem do gráfico, representando uma temperatura de zero absoluto.

Q9.2.6

Como o gráfico na Figura mudaria se o número de moles de gás na amostra usada para determinar a curva fosse dobrado?

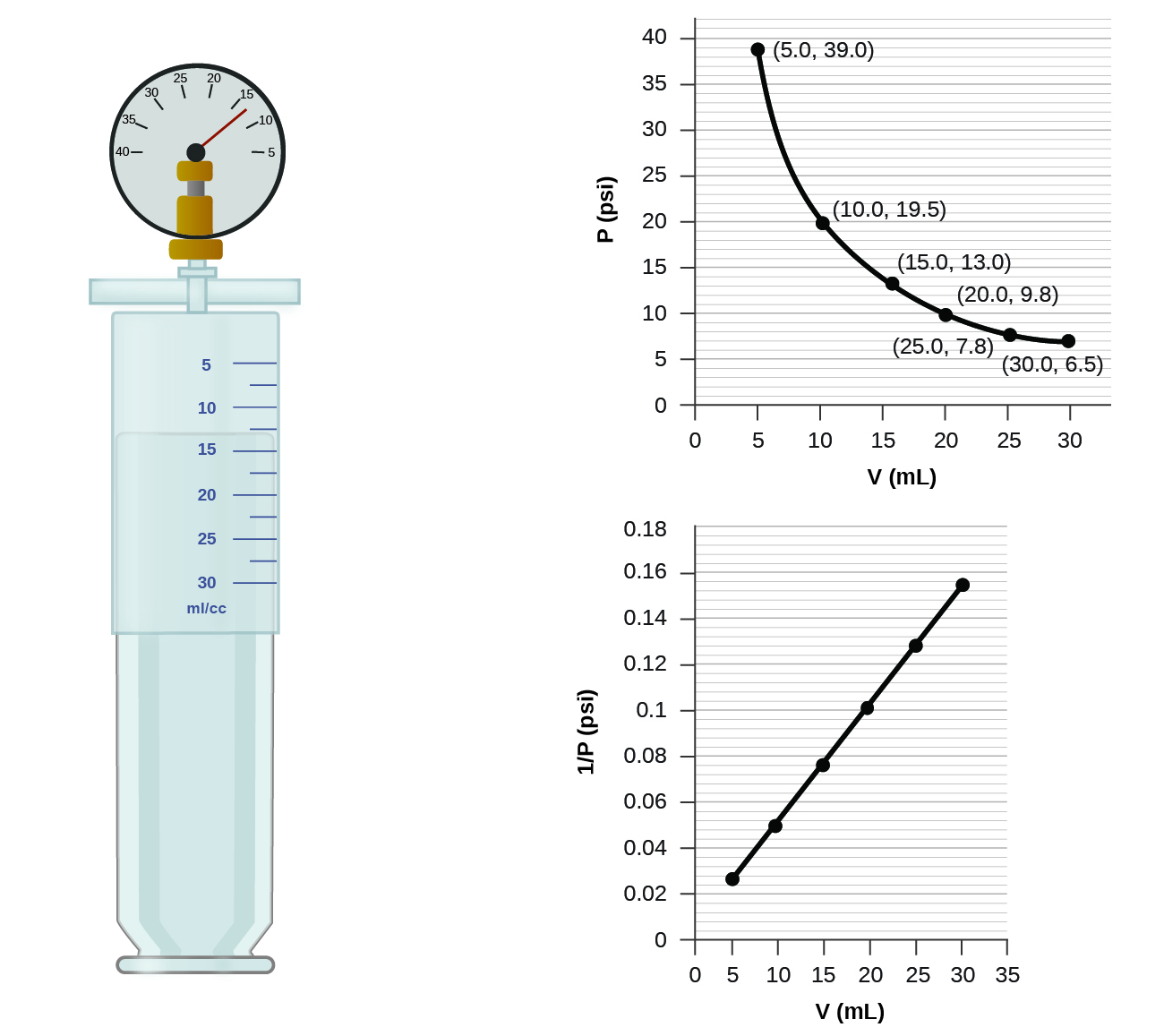
Quando um gás ocupa um volume menor, ele exerce uma pressão maior; quando ocupa um volume maior, exerce uma pressão menor (supondo que a quantidade de gás e a temperatura não mudem). Como P e V são inversamente proporcionais, um gráfico de\(1/P\) vs.\(V\) é linear.

9.2.6

A curva estaria mais à direita e mais acima, mas com a mesma forma básica.

Q9.2.7

Além dos dados encontrados na Figura, quais outras informações precisamos para encontrar a massa da amostra de ar usada para determinar o gráfico?

Q9.2.8

Determine o volume de 1 mol de gás CH ₄ a 150 K e 1 atm, usando a Figura.

9.2.8

16,3 a 16,5 L

Q9.2.9

Determine a pressão do gás na seringa mostrada na Figura quando seu volume é de 12,5 mL, usando:

o gráfico apropriado
Lei de Boyle

Q9.2.10

Uma lata de spray é usada até ficar vazia, exceto pelo gás propulsor, que tem uma pressão de 1344 torr a 23 °C. Se a lata for lançada no fogo (T = 475 °C), qual será a pressão na lata quente?

S 9.2.10

3,40 × 10 ³ torr

Q9.2.11

Qual é a temperatura de uma amostra de 11,2 L de monóxido de carbono, CO, a 74 torr se ela ocupar 13,3 L a 55° C e 74 torr?

S9.2.11

devemos usar\(\dfrac{P_1V_1}{T_1} =\dfrac{P_2V_2}{T_2}\) e resolver para\(T_1\)

\(T_1 = \dfrac{P_1V_1T_2}{P_2V_2}\)

Onde:

\(P_1 = 744\: torr\)

\(V_1 = 11.2\: L\)

\(P_2 = 744\: torr\)

\(V_2 = 13.3\: L\)

\(T_2 = 328.15°\: K\)

\(\dfrac{(744\: torr)(11.2\: L)(328.15°\: K)}{(744\: torr)(13.3\: L)} = 276°\: K\)

276°K; 3°C

Q9.2.12

Um volume de 2,50 L de hidrogênio medido a —196 °C é aquecido a 100 °C. Calcule o volume do gás na temperatura mais alta, assumindo que não há alteração na pressão.

S9.2.13

12,1 L

Q9.2.14

Um balão inflado com três respirações de ar tem um volume de 1,7 L. Na mesma temperatura e pressão, qual é o volume do balão se mais cinco respirações do mesmo tamanho forem adicionadas ao balão?

Q9.2.15

Um balão meteorológico contém 8,80 moles de hélio a uma pressão de 0,992 atm e uma temperatura de 25 °C ao nível do solo. Qual é o volume do balão nessas condições?

S 9.2.15

217 L

Q9.2.16

O volume de um airbag de automóvel era de 66,8 L quando inflado a 25 °C com 77,8 g de gás nitrogênio. Qual era a pressão na bolsa em kPa?

Q9.2.17

Quantos moles de trifluoreto de boro gasoso, BF ₃, estão contidos em uma lâmpada de 4.3410-L a 788,0 K se a pressão for 1.220 atm? Quantos gramas de BF ₃?

S9.2.17

8,190 × 10 ^—2 mol; 5,553 g

Q9.2.18

O iodo, I ₂, é um sólido à temperatura ambiente, mas sublima (converte-se de sólido em gás) quando aquecido. Qual é a temperatura em uma lâmpada de 73,3 mL que contém 0,292 g de vapor I ₂ a uma pressão de 0,462 atm?

S9.2.18

1.) Use a equação\(PV =nRT\) and solve for \(T\)

\(T= \dfrac{PV}{nR}\)

2.) convert grams of I₂ to moles of I₂ and convert mL to L

\(0.292g\: \ce{I2}\times \dfrac{1\: mole\: \ce{I2}}{253.8g\: \ce{I2}} = 1.15 \times10^{-3}\: moles\: \ce{I2}\)

\(73.3\:mL = 0.0733\:L\)

3.) Use these values along with \(R= 0.08206\: \dfrac{atm\:L}{mole\:°K}\) to solve for \(T\)

\(T= \dfrac{(0.462\: \cancel{atm})(0.0733\:\cancel{L})}{(1.15\times10^{-3}\: \cancel{moles})(0.08206\: \dfrac{\cancel{atm}\:\cancel{L}}{\cancel{mole}\:°K})} = 359\: °K \)

359°K ; 86°C

Q9.2.19

How many grams of gas are present in each of the following cases?

0.100 L of CO₂ at 307 torr and 26 °C
8.75 L of C₂H₄, at 378.3 kPa and 483 K
221 mL of Ar at 0.23 torr and –54 °C

S9.2.19

(a) 7.24 × 10^–2 g; (b) 23.1 g; (c) 1.5 × 10^–4 g

Q9.2.20

A high altitude balloon is filled with 1.41 × 10⁴ L of hydrogen at a temperature of 21 °C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?

Q9.2.21

A cylinder of medical oxygen has a volume of 35.4 L, and contains O₂ at a pressure of 151 atm and a temperature of 25 °C. What volume of O₂ does this correspond to at normal body conditions, that is, 1 atm and 37 °C?

S9.2.21

5561 L

Q9.2.22

A large scuba tank (Figure) with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?

Q9.2.23

A 20.0-L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.

S9.2.23

46.4 g

Q9.2.24

While resting, the average 70-kg human male consumes 14 L of pure O₂ per hour at 25 °C and 100 kPa. How many moles of O₂ are consumed by a 70 kg man while resting for 1.0 h?

Q9.2.25

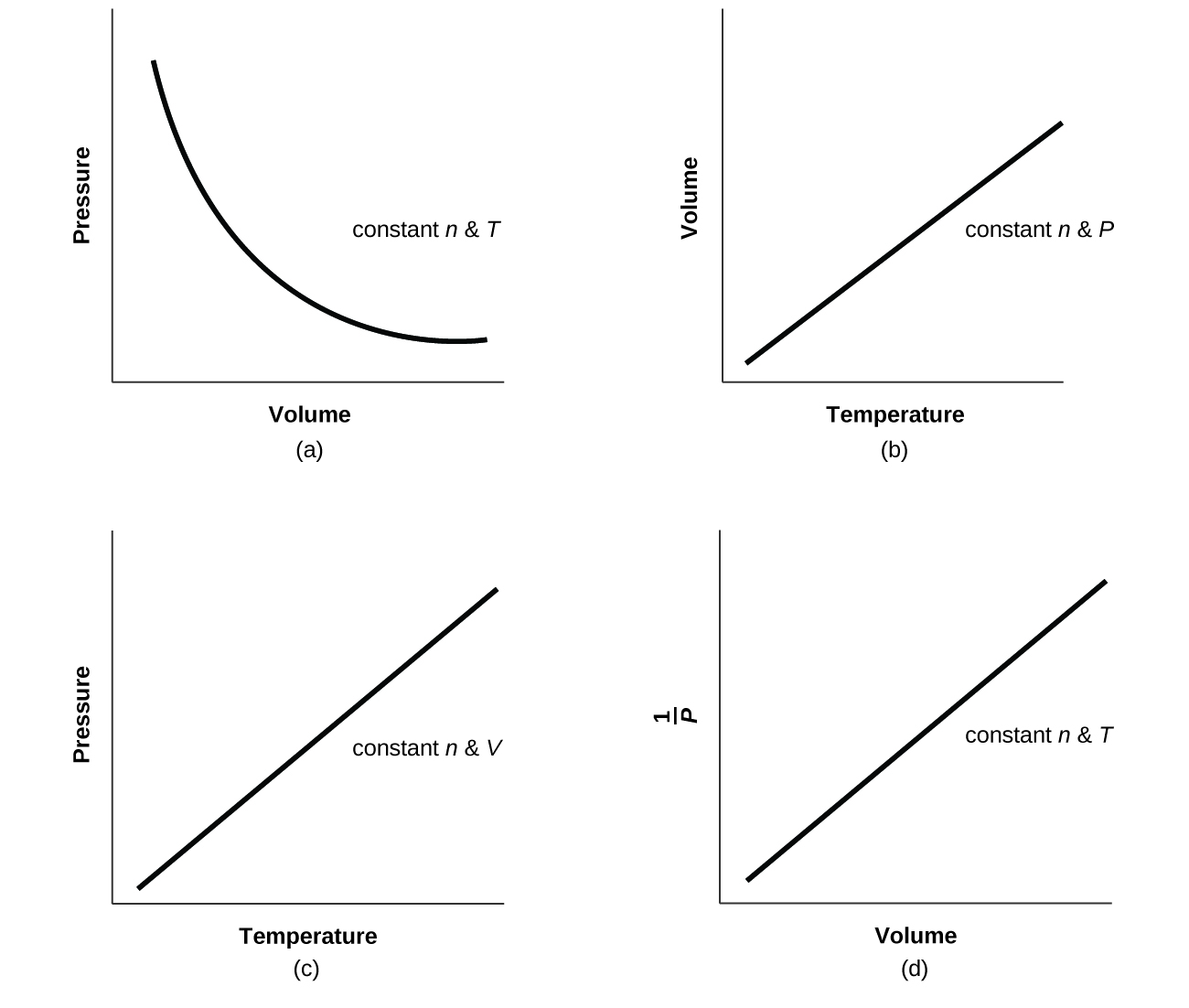
For a given amount of gas showing ideal behavior, draw labeled graphs of:

the variation of P with V
the variation of V with T
the variation of P with T
the variation of \(\dfrac{1}{P}\) with V

Q9.2.26

For a gas exhibiting ideal behavior:

Q9.2.27

Um litro de gás metano, CH ₄, no STP contém mais átomos de hidrogênio do que um litro de gás hidrogênio puro, H ₂, no STP. Usando a lei de Avogadro como ponto de partida, explique o porquê.

Q9.2.28

O efeito dos clorofluorcarbonetos (como CCl ₂ F ₂) na depleção da camada de ozônio é bem conhecido. O uso de substitutos, como CH ₃ CH ₂ F (g), para os clorofluorcarbonetos, corrigiu amplamente o problema. Calcule o volume ocupado por 10,0 g de cada um desses compostos no STP:

CCl ₂ F (₂ g)
CH ₃ CH ₂ F (g)

S9.2.28

(a) 1,85 L CCl ₂ F ₂; (b) 4,66 L CH ₃ CH ₂ F

Q9.2.29

Como 1 g do elemento radioativo rádio decai ao longo de 1 ano, ele produz 1,16 × 10 ¹⁸ partículas alfa (núcleos de hélio). Cada partícula alfa se torna um átomo de gás hélio. Qual é a pressão em pascal do gás hélio produzido se ele ocupa um volume de 125 mL a uma temperatura de 25 °C?

Q9.2.30

Um balão de 100,21 L a 21 °C e 0,981 atm é lançado e mal chega ao topo do Monte Crumpet, na Colúmbia Britânica. Se o volume final do balão for 144,53 L a uma temperatura de 5,24 °C, qual é a pressão sentida pelo balão ao limpar o Monte Crumpet?

S 9.2.30

0,644 atm

Q9.2.31

Se a temperatura de uma quantidade fixa de gás for dobrada em volume constante, o que acontece com a pressão?

Q9.2.32

Se o volume de uma quantidade fixa de gás for triplicado em temperatura constante, o que acontece com a pressão?

S9.2.32

A pressão diminui em um fator de 3.

9.3: Estequiometria de substâncias gasosas, misturas e reações

Q9.3.1

Qual é a densidade do gás do riso, monóxido de dinitrogênio, N ₂ O, a uma temperatura de 325 K e uma pressão de 113,0 kPa?

S9.3.1

1.) Primeiro converta kPa em atm

\(113.0\:kPa\times\dfrac{1\:atm}{101.325\:kPa}=1.115\:atm\)

2.) Use a equação em\(d=\dfrac{PM}{RT}\) que d = densidade em g L ^-1 e M = massa molar em g mol ^-1

\(d=\dfrac{(1.115\:atm)(44.02\dfrac{g}{\cancel{mol}})}{(0.08206\: \dfrac{\cancel{atm}\:L}{\cancel{mole}\:\cancel{°K}})(325\:\cancel{°K})}=1.84\:\dfrac{g}{L}\)

Q9.3.2

Calcule a densidade de Freon 12, CF ₂ _{Cl 2}, a 30,0 °C e 0,954 atm.

S9.3.2

4,64 g L ⁻¹

Q9.3.3

Qual é mais denso na mesma temperatura e pressão, ar seco ou ar saturado com vapor de água? Explique.

Q9.3.4

Um cilindro de O ₂ (g) usado na respiração de pacientes com enfisema tem um volume de 3,00 L a uma pressão de 10,0 atm. Se a temperatura do cilindro for 28,0 °C, qual massa de oxigênio está no cilindro?

9.3.4

38,8 g

Q9.3.5

Qual é a massa molar de um gás se 0,0494 g do gás ocupar um volume de 0,100 L a uma temperatura de 26° C e uma pressão de 307 torr?

S 9.3.5

1.) converter torr em atm e °C em K

\(307\:torr=0.404atm\)

\(26°C= 300.°K\)

2.) Use a equação\(PV=nRT\) e resolva para\(n\)

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(0.404\:\cancel{atm})(0.100\:\cancel{L})}{(0.08206\dfrac{\cancel{atm}\:\cancel{L}}{mol\:\cancel{°K}})(300.\cancel{°K})}=0.00165\:moles\)

3.) Em seguida, divida os gramas pelo número de moles para obter a massa molar:

\(\dfrac{0.0494g}{0.00165\:moles}=30.0\dfrac{g}{mole}\)

Q9.3.6

Qual é a massa molar de um gás se 0,281 g do gás ocupar um volume de 125 mL a uma temperatura de 126 °C e uma pressão de 777 torr?

9.3.6

72,0 g mol ⁻¹

Q9.3.7

Como você pode mostrar experimentalmente que a fórmula molecular do propeno é C ₃ H ₆, não CH ₂?

Q9.3.8

A densidade de um determinado fluoreto gasoso de fósforo é de 3,93 g/L no STP. Calcule a massa molar desse flúor e determine sua fórmula molecular.

9.3.8

88,1 g mol ⁻¹; PF ₃

Q9.3.9

Considere esta pergunta: Qual é a fórmula molecular de um composto que contém 39% C, 45% N e 16% H se 0,157 g do composto ocupar 125 mL com uma pressão de 99,5 kPa a 22 °C?

Descreva as etapas necessárias para responder à pergunta.
Responda à pergunta.

Q9.3.10

Um cilindro de 36,0—L de um gás usado para calibração de analisadores de gases sanguíneos em laboratórios médicos contém 350 g de CO ₂, 805 g O ₂ e 4.880 g N ₂. A 25 graus C, qual é a pressão no cilindro nas atmosferas?

S 9.3.10

141 caixa eletrônico

Q9.3.11

Um cilindro de uma mistura gasosa usado para calibração de analisadores de gasometria em laboratórios médicos contém 5,0% de CO _₂, 12,0% de O 2 e o restante N ₂ a uma pressão total de 146 atm. Qual é a pressão parcial de cada componente desse gás? (As porcentagens fornecidas indicam a porcentagem da pressão total devida a cada componente.)

Q9.3.12

Uma amostra de gás isolada de petróleo não refinado contém 90,0% CH ₄, 8,9% C ₂ H ₆ e 1,1% C ₃ H ₈ a uma pressão total de 307,2 kPa. Qual é a pressão parcial de cada componente desse gás? (As porcentagens fornecidas indicam a porcentagem da pressão total devida a cada componente.)

9.3.12

CH ₄: 276 kPa; C ₂ H ₆: 27 kPa; C ₃ H ₈: 3,4 kPa

Q9.3.13

Uma mistura de 0,200 g de H ₂, 1,00 g de N ₂ e 0,820 g de Ar é armazenada em um recipiente fechado no STP. Determine o volume do recipiente, assumindo que os gases exibem um comportamento ideal.

Q9.3.14

A maioria das misturas de gás hidrogênio com gás oxigênio são explosivas. No entanto, uma mistura que contém menos de 3,0% de O ₂ não é. Se for adicionado O ₂ suficiente a um cilindro de H ₂ a 33,2 atm para elevar a pressão total a 34,5 atm, a mistura é explosiva?

S 9.3.14

sim

Q9.3.15

Um analisador comercial de vapor de mercúrio pode detectar, no ar, concentrações de átomos gasosos de Hg (que são venenosos) tão baixas quanto 2 × 10 ⁻⁶ mg/L de ar. Nessa concentração, qual é a pressão parcial do mercúrio gasoso se a pressão atmosférica for de 733 torr a 26 °C?

Q9.3.16

Uma amostra de monóxido de carbono foi coletada sobre a água a uma pressão total de 756 torr e uma temperatura de 18 °C. Qual é a pressão do monóxido de carbono? (Consulte a tabela para ver a pressão de vapor da água.)

S9.3.16

740 torr

Q9.3.17

Em um experimento em um laboratório de química geral, um estudante coletou uma amostra de um gás sobre a água. O volume do gás foi de 265 mL a uma pressão de 753 torr e uma temperatura de 27 °C. A massa do gás foi de 0,472 g. Qual era a massa molar do gás?

Q9.3.18

Joseph Priestley primeiro preparou oxigênio puro aquecendo o óxido mercúrico, HgO:

\(\ce{2HgO}(s)⟶\ce{2Hg}(l)+\ce{O2}(g)\)

Descreva as etapas necessárias para responder à seguinte pergunta: Qual volume de O ₂ a 23 °C e 0,975 atm é produzido pela decomposição de 5,36 g de HgO?
Responda à pergunta.

9.3.18

(a) Determine os moles de HgO que se decompõem; usando a equação química, determine os moles de O ₂ produzidos pela decomposição dessa quantidade de HgO; e determine o volume de O ₂ a partir dos moles de O ₂, temperatura e pressão. (b) 0,308 L

Q9.3.19

Cavendish preparou hidrogênio em 1766 pelo novo método de passar vapor por um cano de arma em brasa:

\[\ce{4H2O}(g)+\ce{3Fe}(s)⟶\ce{Fe3O4}(s)+\ce{4H2}(g)\]

Descreva as etapas necessárias para responder à seguinte pergunta: Qual volume de H ₂ a uma pressão de 745 torr e uma temperatura de 20° C pode ser preparado a partir da reação de 15,O g de H ₂ O?
Responda à pergunta.

Q9.3.20

O clorofluorocarbono CCl ₂ F ₂ pode ser reciclado em um composto diferente por reação com hidrogênio para produzir CH ₂ F ₂ (g), um composto útil na fabricação de produtos químicos:

\[\ce{CCl2F2}(g)+\ce{4H2}(g)⟶\ce{CH2F2}(g)+\ce{2HCl}(g)\]

Descreva as etapas necessárias para responder à seguinte pergunta: Qual volume de hidrogênio a 225 atm e 35,5° C seria necessário para reagir com 1 tonelada (1.000 × 10 ³ kg) de CCl ₂ F ₂?
Responda à pergunta.

S 9.3.20

Determine a massa molar de CcL ₂ F ₂. A partir da equação balanceada, calcule os moles de H ₂ necessários para a reação completa. A partir da lei do gás ideal, converta moles de H ₂ em volume.
3,72 × 10 ³ L

Q9.3.21

Os airbags de automóveis são inflados com gás nitrogênio, que é formado pela decomposição da azida de sódio sólida (NaN ₃). O outro produto é metal sódico. Calcule o volume de gás nitrogênio a 27 °C e 756 torr formado pela decomposição de 125 g de azida de sódio.

Q9.3.22

A cal, CaO, é produzida pelo aquecimento do carbonato de cálcio, CaCO ₃; o dióxido de carbono é o outro produto.

Descreva as etapas necessárias para responder à seguinte pergunta: Qual volume de dióxido de carbono a 875° e 0,966 atm é produzido pela decomposição de 1 tonelada (1.000 × 10 ³ kg) de carbonato de cálcio?
Responda à pergunta.

S9.3.22

(a) Equilibre a equação. Determine os gramas de CO ₂ produzidos e o número de moles. A partir da lei do gás ideal, determine o volume do gás. (b) 7,43 × 10 ⁵ L

Q9.3.23

Antes que as baterias pequenas estivessem disponíveis, lâmpadas de metal duro eram usadas para luzes de bicicleta. O gás acetileno, C ₂ _{H 2} e o hidróxido de cálcio sólido foram formados pela reação do carboneto de cálcio, CaC ₂, com a água. A ignição do gás acetileno forneceu a luz. Atualmente, as mesmas lâmpadas são usadas por alguns espeleólogos e o carboneto de cálcio é usado para produzir acetileno para canhões de carboneto.

Descreva as etapas necessárias para responder à seguinte pergunta: Qual volume de C ₂ H ₂ a 1,005 atm e 12,2° C é formado pela reação de 15,48 g de CaC ₂ com água?
Responda à pergunta.

Q9.3.24

Calcule o volume de oxigênio necessário para queimar 12,00 L de gás etano, C ₂ H ₆, para produzir dióxido de carbono e água, se os volumes de C ₂ H ₆ e O ₂ forem medidos nas mesmas condições de temperatura e pressão.

9.3.24

42,00 L

Q9.3.25

Qual volume de O ₂ no STP é necessário para oxidar 8,0 L de NO no STP para NO ₂? Qual volume de NO ₂ é produzido no STP?

Q9.3.26

Considere as seguintes perguntas:

Qual é o volume total de CO ₂ (g) e H ₂ O (g) a 600 °C e 0,888 atm produzido pela combustão de 1,00 L de C ₂ H ₆ (g) medido no STP?
Qual é a pressão parcial de H ₂ O nos gases do produto?

S 9.3.26

(a) 18,0 L; (b) 0,533 atm

Q9.3.27

O metanol, CH ₃ OH, é produzido industrialmente pela seguinte reação:

\[\ce{CO}(g)+\ce{2H2}(g)\xrightarrow{\textrm{ copper catalyst 300 °C, 300 atm }}\ce{CH3OH}(g)\]

Q9.3.28

Supondo que os gases se comportem como gases ideais, determine a razão entre o volume total dos reagentes e o volume final.

Q9.3.29

Qual volume de oxigênio a 423,0 K e pressão de 127,4 kPa é produzido pela decomposição de 129,7 g de BaO ₂ em BaO e O ₂?

S 9.3.29

10,57 L OU ₂

Q9.3.30

Uma amostra de 2,50 L de um gás incolor em STP decomposta para dar 2,50 L de N ₂ e 1,25 L de O ₂ no STP. O que é o gás incolor?

Q9.3.31

O etanol, C ₂ H ₅ OH, é produzido industrialmente a partir do etileno, C ₂ H ₄, pela seguinte sequência de reações:

\[\ce{3C2H4 + 2H2SO4⟶C2H5HSO4 + (C2H5)2SO4}\]

\[\ce{C2H5HSO4 + (C2H5)2SO4 + 3H2O⟶3C2H5OH + 2H2SO4}\]

Qual volume de etileno no STP é necessário para produzir 1.000 toneladas métricas (1000 kg) de etanol se o rendimento geral do etanol for 90,1%?

9.3.31

5,40 × 10 ⁵ L

Q9.3.32

Uma molécula de hemoglobina se combinará com quatro moléculas de oxigênio. Se 1,0 g de hemoglobina se combina com 1,53 mL de oxigênio à temperatura corporal (37 °C) e uma pressão de 743 torr, qual é a massa molar da hemoglobina?

Q9.3.33

Uma amostra de um composto de xenônio e flúor foi confinada em uma lâmpada com uma pressão de 18 torr. O hidrogênio foi adicionado à lâmpada até que a pressão fosse de 72 torr. A passagem de uma faísca elétrica pela mistura produziu Xe e HF. Depois que o HF foi removido por reação com KOH sólido, a pressão final do xenônio e do hidrogênio não reagido no bulbo foi de 36 torr. Qual é a fórmula empírica do fluoreto de xenônio na amostra original? (Nota: Os fluoretos de xenônio contêm apenas um átomo de xenônio por molécula.)

9.3.33

Ef ₂

Q9.3.34

Um método de análise de aminoácidos é o método van Slyke. Os grupos amino característicos (−NH ₂) no material proteico podem reagir com o ácido nitroso, HNO ₂, para formar o gás N ₂. A partir do volume do gás, a quantidade de aminoácido pode ser determinada. Uma amostra de 0,0604 g de uma amostra biológica contendo glicina, CH ₂ (NH ₂) COOH, foi analisada pelo método van Slyke e produziu 3,70 mL de N ₂ coletado sobre a água a uma pressão de 735 torr e 29 °C. Qual foi a porcentagem de glicina na amostra?

\(\ce{CH2(NH2)CO2H + HNO2⟶CH2(OH)CO2H + H2O + N2}\)

9.4: Efusão e difusão de gases

Q9.4.1

Descobriu-se que um balão cheio de gás hélio leva 6 horas para desinflar até 50% de seu volume original. Quanto tempo será necessário para que um balão idêntico cheio com o mesmo volume de gás hidrogênio (em vez de hélio) diminua seu volume em 50%?

S9.4.1

4,2 horas

Q9.4.2

Explique por que o número de moléculas não é idêntico nas lâmpadas esquerda e direita mostradas na ilustração central da Figura.

Q9.4.3

Começando com a definição de taxa de efusão e a descoberta de Graham relacionando taxa e massa molar, mostre como derivar a equação da lei de Graham, relacionando as taxas relativas de efusão de dois gases com suas massas moleculares.

S9.4.3

O efusão pode ser definido como o processo pelo qual um gás escapa através de um orifício para o vácuo. A lei de Graham afirma que com uma mistura de dois gases A e B:\(\mathrm{\left(\dfrac{rate\: A}{rate\: B}\right)=\left(\dfrac{molar\: mass\: of\: B}{molar\: mass\: of\: A}\right)^{1/2}}\). Tanto A quanto B estão no mesmo recipiente na mesma temperatura e, portanto, terão a mesma energia cinética:

\(\mathrm{KE_A=KE_BKE}=\dfrac{1}{2}mv^2\) Portanto,\(\dfrac{1}{2}m_\ce{A}v^2_\ce{A}=\dfrac{1}{2}m_\ce{B}v^2_\ce{B}\) \(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}=\dfrac{m_\ce{B}}{m_\ce{A}}\) \(\left(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}\right)^{1/2}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\) \(\dfrac{v_\ce{A}}{v_\ce{B}}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\)

Q9.4.4

A água pesada, D ₂ O (massa molar = 20,03 g mol ^—1), pode ser separada da água comum, H ₂ O (massa molar = 18,01), como resultado da diferença nas taxas relativas de difusão das moléculas na fase gasosa. Calcule as taxas relativas de difusão de H ₂ O e D ₂ O.

Q9.4.5

Qual dos seguintes gases se difunde mais lentamente que o oxigênio? F ₂, Ne, N ₂ O, C ₂ H ₂, NÃO, Cl ₂, H ₂ S

S 9.4.5

F ₂, N ₂ O, Cl ₂, H ₂ S

Q9.4.6

Durante a discussão sobre difusão gasosa para enriquecer urânio, foi alegado que ²³⁵ UF ₆ se difunde 0,4% mais rápido do que ²³⁸ UF ₆. Mostre o cálculo que suporta esse valor. A massa molar de ²³⁵ UF ₆ = 235,043930 + 6 × 18,998403 = 349,034348 g/mol e a massa molar de ²³⁸ UF ₆ = 238,050788 + 6 × 18,998403 = 352,041206 g/mol.

Q9.4.7

Calcule a taxa relativa de difusão de ¹ H ₂ (massa molar 2,0 g/mol) em comparação com a de ² _{H 2} (massa molar 4,0 g/mol) e a taxa relativa de difusão de O ₂ (massa molar 32 g/mol) em comparação com a de O ₃ (massa molar 48 g/mol).

9.4.7

1,4; 1,2

Q9.4.8

Um gás de identidade desconhecida se difunde a uma taxa de 83,3 mL/s em um aparelho de difusão no qual o dióxido de carbono se difunde à taxa de 102 mL/s. Calcule a massa molecular do gás desconhecido.

Q9.4.9

Quando dois tampões de algodão, um umedecido com amônia e outro com ácido clorídrico, são inseridos simultaneamente nas extremidades opostas de um tubo de vidro com 87,0 cm de comprimento, um anel branco de NH ₄ Cl se forma onde o NH ₃ gasoso e o HCl gasoso entram em contato pela primeira vez. (Dica: calcule as taxas de difusão do NH ₃ e do HCl e descubra quanto mais rápido o NH ₃ se difunde do que o HCl.)

\[\ce{NH3}(g)+\ce{HCl}(g)⟶\ce{NH4Cl}(s)\]

Q9.4.10

Aproximadamente a que distância do tampão umedecido com amônia isso ocorre?

S 9.4.10

51,7 cm

9.5: A Teoria Cinético-Molecular

Q9.5.1

Usando os postulados da teoria molecular cinética, explique por que um gás preenche uniformemente um recipiente de qualquer formato.

Q9.5.2

A velocidade de uma determinada molécula em um gás pode dobrar em temperatura constante? Explique sua resposta.

9.5.2

Sim. Em qualquer instante, há uma variedade de valores de velocidades moleculares em uma amostra de gás. Qualquer molécula única pode acelerar ou diminuir a velocidade ao colidir com outras moléculas. A velocidade média de todas as moléculas é constante em temperatura constante.

Q9.5.3

Descreva o que acontece com a energia cinética média das moléculas de gás ideais quando as condições são alteradas da seguinte forma:

A pressão do gás é aumentada pela redução do volume em temperatura constante.
A pressão do gás é aumentada aumentando a temperatura em volume constante.
A velocidade média das moléculas é aumentada por um fator de 2.

Q9.5.4

A distribuição das velocidades moleculares em uma amostra de hélio é mostrada na Figura. Se a amostra for resfriada, a distribuição das velocidades será mais parecida com a de H ₂ ou de H ₂ O? Explique sua resposta.

9.5.4

H ₂ O. O resfriamento diminui a velocidade dos átomos de He, fazendo com que eles se comportem como se fossem mais pesados.

Q9.5.5

Qual é a razão entre a energia cinética média de uma molécula de SO ₂ e a de uma molécula de O ₂ em uma mistura de dois gases? Qual é a razão entre as velocidades quadradas médias, u _rms, dos dois gases?

Q9.5.6

Uma amostra de 1 L de CO inicialmente no STP é aquecida a 546° C e seu volume é aumentado para 2 L.

Que efeito essas mudanças têm no número de colisões das moléculas do gás por unidade de área da parede do recipiente?
Qual é o efeito na energia cinética média das moléculas?
Qual é o efeito na velocidade quadrada média das moléculas?

9.5.6

(a) O número de colisões por unidade de área da parede do contêiner é constante. (b) A energia cinética média dobra. (c) A velocidade quadrada média aumenta para\(\sqrt{2}\) vezes seu valor inicial; u _rms é proporcional\(\mathrm{KE_{avg}}\) a.

Q9.5.7

A velocidade quadrada média da raiz das moléculas de H ₂ a 25 °C é de cerca de 1,6 km/s. Qual é a velocidade quadrada média da raiz de uma molécula de N ₂ a 25 °C?

Q9.5.8

Responda às seguintes perguntas:

A pressão do gás no balão de ar quente mostrado na abertura deste capítulo é maior, menor ou igual à da atmosfera fora do balão?
A densidade do gás no balão de ar quente mostrado na abertura deste capítulo é maior, menor ou igual à da atmosfera fora do balão?
A uma pressão de 1 atm e uma temperatura de 20 °C, o ar seco tem uma densidade de 1,2256 g/L. Qual é a massa molar (média) do ar seco?
A temperatura média do gás em um balão de ar quente é 1,30 × 10 ² °F. Calcule sua densidade, assumindo que a massa molar é igual à do ar seco.
A capacidade de elevação de um balão de ar quente é igual à diferença entre a massa do ar frio deslocado pelo balão e a massa do gás no balão. Qual é a diferença na massa de 1,00 L do ar frio na parte (c) e do ar quente na parte (d)?
Um balão médio tem um diâmetro de 60 pés e um volume de 1,1 × 10 ⁵ pés ³. Qual é o poder de elevação desse balão? Se o peso do balão e seu cordame for de 500 libras, qual é sua capacidade para transportar passageiros e cargas?
Um balão carrega 40,0 galões de propano líquido (densidade 0,5005 g/L). Qual volume de gás CO ₂ _{e H 2} O é produzido pela combustão desse propano?
Um voo de balão pode durar cerca de 90 minutos. Se todo o combustível for queimado durante esse período, qual é a taxa aproximada de perda de calor (em kJ/min) do ar quente na bolsa durante o voo?

S9.5.1

(a) igual; (b) menor que; (c) 29,48 g mol ⁻¹; (d) 1,0966 g L ⁻¹; (e) 0,129 g/L; (f) 4,01 × 10 ⁵ g; capacidade líquida de elevação = 384 lb; (g) 270 L; (h) 39,1 kJ min ⁻¹

Q9.5.1

Mostre que a razão entre a taxa de difusão do gás 1 e a taxa de difusão do gás 2,\(\dfrac{R_1}{R_2}\), é a mesma a 0 °C e 100 °C.

9.6: Comportamento não ideal do gás

Q9.6.1

Seguem gráficos mostrando o comportamento de vários gases diferentes. Quais desses gases apresentam um comportamento significativamente diferente do esperado para gases ideais?

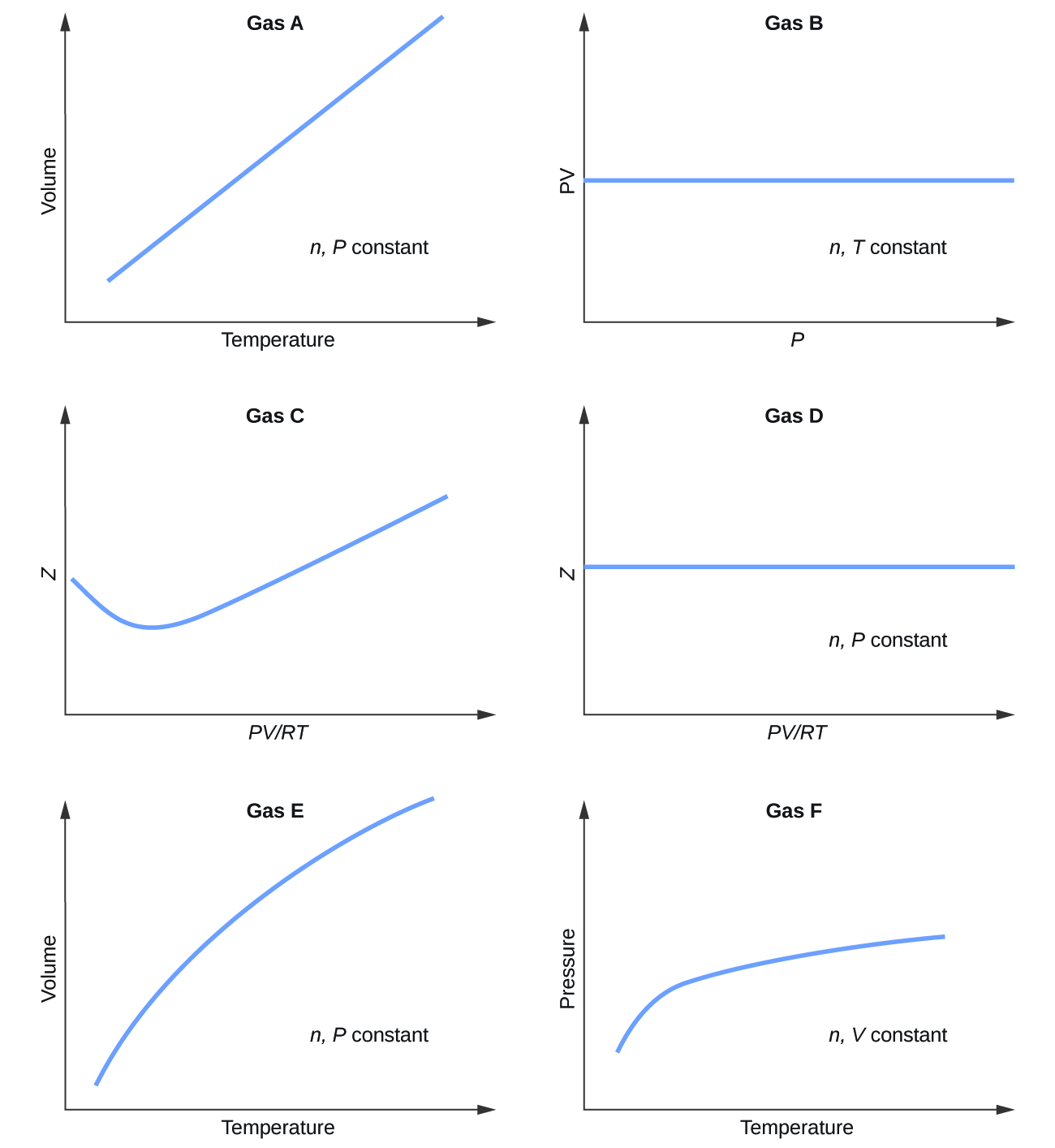
S9.6.1

Gases C, E e F

Q9.6.3

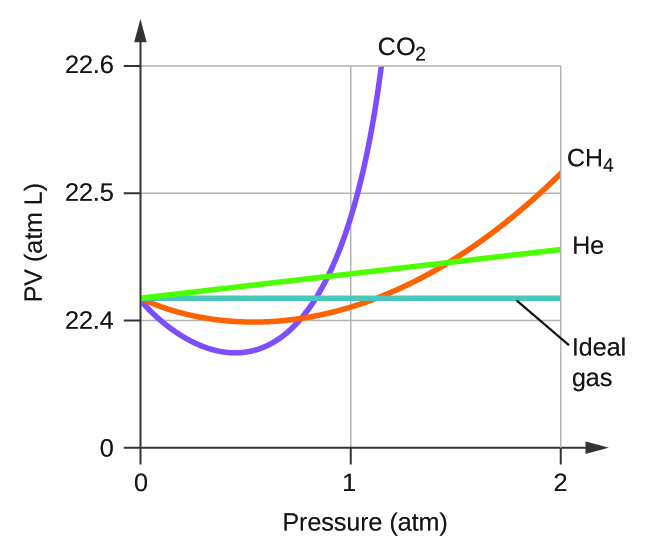
Explique por que o gráfico de PV para CO ₂ difere daquele de um gás ideal.

Q9.6.3

Sob qual dos seguintes conjuntos de condições um gás real se comporta mais como um gás ideal e para quais condições se espera que um gás real se desvie do comportamento ideal? Explique.

alta pressão, pequeno volume
alta temperatura, baixa pressão
baixa temperatura, alta pressão

9.6.3

O comportamento do gás mais parecido com um gás ideal ocorrerá nas condições em (b). As moléculas têm altas velocidades e se movem por distâncias maiores entre as colisões; elas também têm tempos de contato mais curtos e as interações são menos prováveis. Os desvios ocorrem com as condições descritas em (a) e (c). Sob as condições de (a), alguns gases podem se liquefazer. Sob as condições de (c), a maioria dos gases se liquefaz.

Q9.6.4

Descreva os fatores responsáveis pelo desvio do comportamento dos gases reais em relação ao de um gás ideal.

Q9.6.5

Para qual dos seguintes gases a correção do volume molecular deve ser maior: CO, CO _{2, H ₂}, He, NH ₃, SF ₆?

9.6.6

SF ₆

Q9.6.7

Um frasco de 0,245 L contém 0,467 mol de CO ₂ a 159 °C. Calcule a pressão:

usando a lei do gás ideal
usando a equação de van der Waals
Explique o motivo da diferença.
Identifique qual correção (aquela para P ou V) é dominante e por quê.

Q9.6.8

Responda às seguintes perguntas:

Se XX se comportasse como um gás ideal, como seria seu gráfico de Z versus P?
Na maior parte deste capítulo, realizamos cálculos tratando os gases como ideais. Isso foi justificado?
Qual é o efeito do volume das moléculas de gás em Z? Em que condições esse efeito é pequeno? Quando é grande? Explique usando um diagrama apropriado.
Qual é o efeito das atrações intermoleculares no valor de Z? Em que condições esse efeito é pequeno? Quando é grande? Explique usando um diagrama apropriado.
Em geral, sob quais condições de temperatura você esperaria que Z tivesse os maiores desvios do Z para um gás ideal?

9.6.8

(a) Uma linha horizontal reta em 1,0; (b) Quando os gases reais estão em baixas pressões e altas temperaturas, eles se comportam perto o suficiente dos gases ideais para serem aproximados como tal, no entanto, em alguns casos, vemos que em alta pressão e temperatura, a aproximação ideal do gás se rompe e é significativamente diferente da pressão calculada pela equação de van der Waals (c) Quanto maior a compressibilidade, mais o volume importa. Em baixas pressões, o fator de correção para atrações intermoleculares é mais significativo, e o efeito do volume das moléculas de gás em Z seria uma pequena redução da compressibilidade. Em pressões mais altas, o efeito do volume das próprias moléculas de gás em Z aumentaria a compressibilidade (veja a Figura) (d) Mais uma vez, em baixas pressões, o efeito das atrações intermoleculares em Z seria mais importante do que o fator de correção para o volume das moléculas de gás eles mesmos, embora talvez ainda sejam pequenos. Em pressões mais altas e baixas temperaturas, o efeito das atrações intermoleculares seria maior. Veja a Figura. (e) baixas temperaturas

9.6: Comportamento não ideal do gás

Exercícios

Seguem gráficos mostrando o comportamento de vários gases diferentes. Quais desses gases apresentam um comportamento significativamente diferente do esperado para gases ideais?

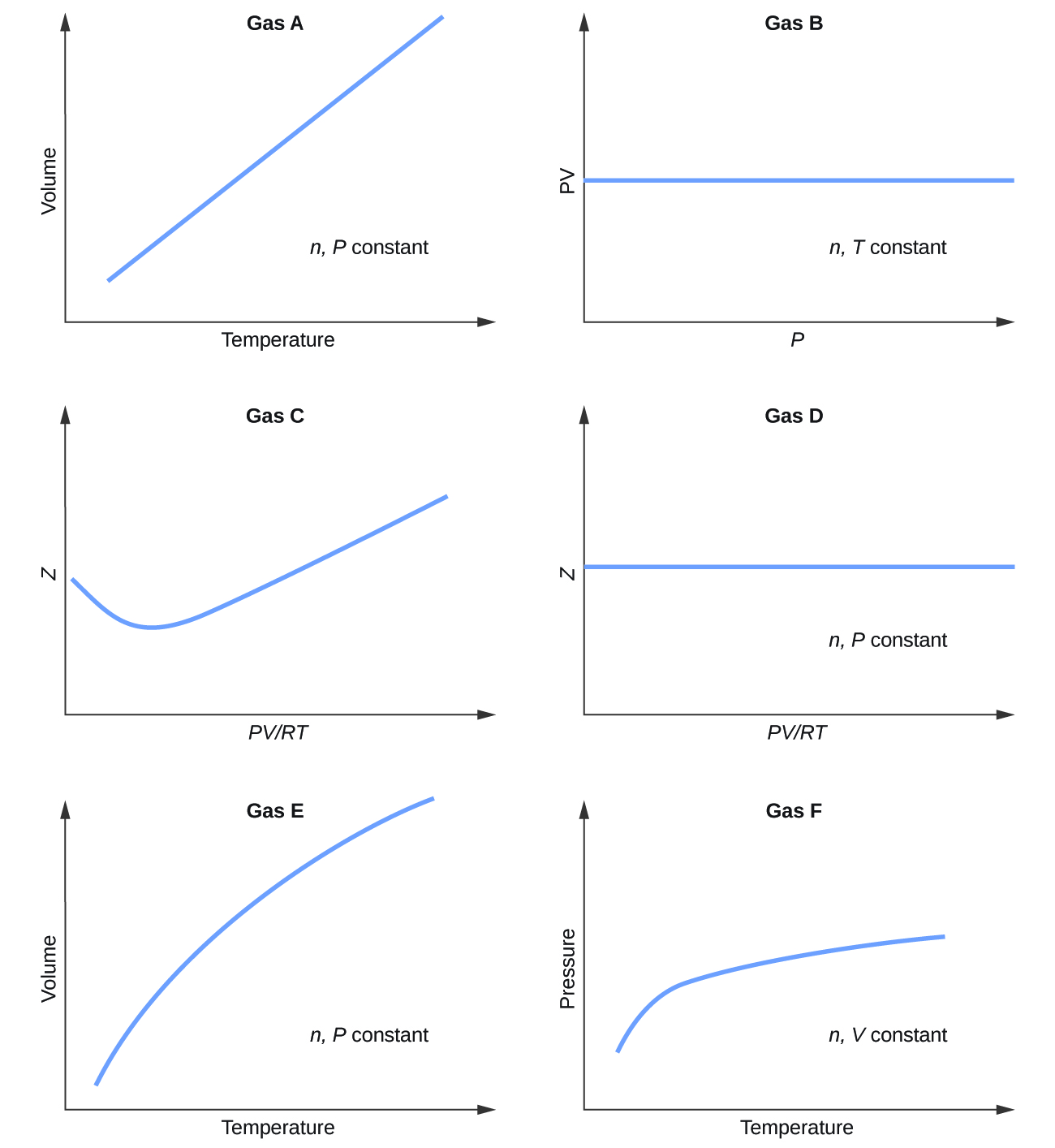
Gases C, E e F

Explique por que o gráfico de PV para CO ₂ difere daquele de um gás ideal.

Sob qual dos seguintes conjuntos de condições um gás real se comporta mais como um gás ideal e para quais condições se espera que um gás real se desvie do comportamento ideal? Explique.

(a) alta pressão, pequeno volume

(b) alta temperatura, baixa pressão

Descreva os fatores responsáveis pelo desvio do comportamento dos gases reais em relação ao de um

gás ideal.

Para qual dos seguintes gases a correção do volume molecular deve ser maior:

CO, CO ₂, H ₂, He, NH ₃, SF ₆?

SF ₆

Um frasco de 0,245 L contém 0,467 mol de CO ₂ a 159 °C. Calcule a pressão:

(a) usando a lei do gás ideal

(b) usando a equação de van der Waals

(d) Identifique qual correção (aquela para P ou V) é dominante e por quê.

Responda às seguintes perguntas:

(a) Se XX se comportasse como um gás ideal, como seria seu gráfico de Z versus P?

(b) Na maior parte deste capítulo, realizamos cálculos tratando os gases como ideais. Isso foi justificado?

(c) Qual é o efeito do volume de moléculas de gás em Z? Em que condições esse efeito é pequeno? Quando é grande? Explique usando um diagrama apropriado.

(d) Qual é o efeito das atrações intermoleculares no valor de Z? Em que condições esse efeito é pequeno? Quando é grande? Explique usando um diagrama apropriado.

(e) Em geral, sob quais condições de temperatura você esperaria que Z tivesse os maiores desvios do Z para um gás ideal?