9.5: A Teoria Cinético-Molecular

Objetivos de

• Declare os postulados da teoria cinético-molecular
• Use os postulados dessa teoria para explicar as leis do gás

As leis dos gases que vimos até agora, assim como a equação ideal do gás, são empíricas, ou seja, foram derivadas de observações experimentais. As formas matemáticas dessas leis descrevem de perto o comportamento macroscópico da maioria dos gases em pressões menores que cerca de 1 ou 2 atm. Embora as leis dos gases descrevam relações que foram verificadas por muitos experimentos, elas não nos dizem por que os gases seguem essas relações.

A teoria molecular cinética (KMT) é um modelo microscópico simples que explica efetivamente as leis dos gases descritas nos módulos anteriores deste capítulo. Essa teoria é baseada nos seguintes cinco postulados descritos aqui. (Nota: O termo “molécula” será usado para se referir às espécies químicas individuais que compõem o gás, embora alguns gases sejam compostos por espécies atômicas, por exemplo, os gases nobres.)

1. Os gases são compostos por moléculas que estão em movimento contínuo, viajando em linhas retas e mudando de direção somente quando colidem com outras moléculas ou com as paredes de um recipiente.
2. As moléculas que compõem o gás são insignificantemente pequenas em comparação com as distâncias entre elas.
3. A pressão exercida por um gás em um recipiente resulta de colisões entre as moléculas do gás e as paredes do recipiente.
4. As moléculas de gás não exercem forças atrativas ou repulsivas umas sobre as outras ou sobre as paredes do recipiente; portanto, suas colisões são elásticas (não envolvem perda de energia).
5. A energia cinética média das moléculas de gás é proporcional à temperatura kelvin do gás.

O teste do KMT e seus postulados é sua capacidade de explicar e descrever o comportamento de um gás. As várias leis dos gases podem ser derivadas das suposições do KMT, que levaram os químicos a acreditar que as suposições da teoria representam com precisão as propriedades das moléculas de gás. Primeiro, examinaremos conceitualmente as leis individuais do gás (leis de Boyle, Charles, Amontons, Avogadro e Dalton) para ver como o KMT as explica. Em seguida, consideraremos com mais cuidado as relações entre massas moleculares, velocidades e energias cinéticas com a temperatura e explicaremos a lei de Graham.

A teoria cinético-molecular explica o comportamento dos gases, parte I

Lembrando que a pressão do gás é exercida por moléculas de gás que se movem rapidamente e depende diretamente do número de moléculas que atingem uma unidade de área da parede por unidade de tempo, vemos que o KMT explica conceitualmente o comportamento de um gás da seguinte forma:

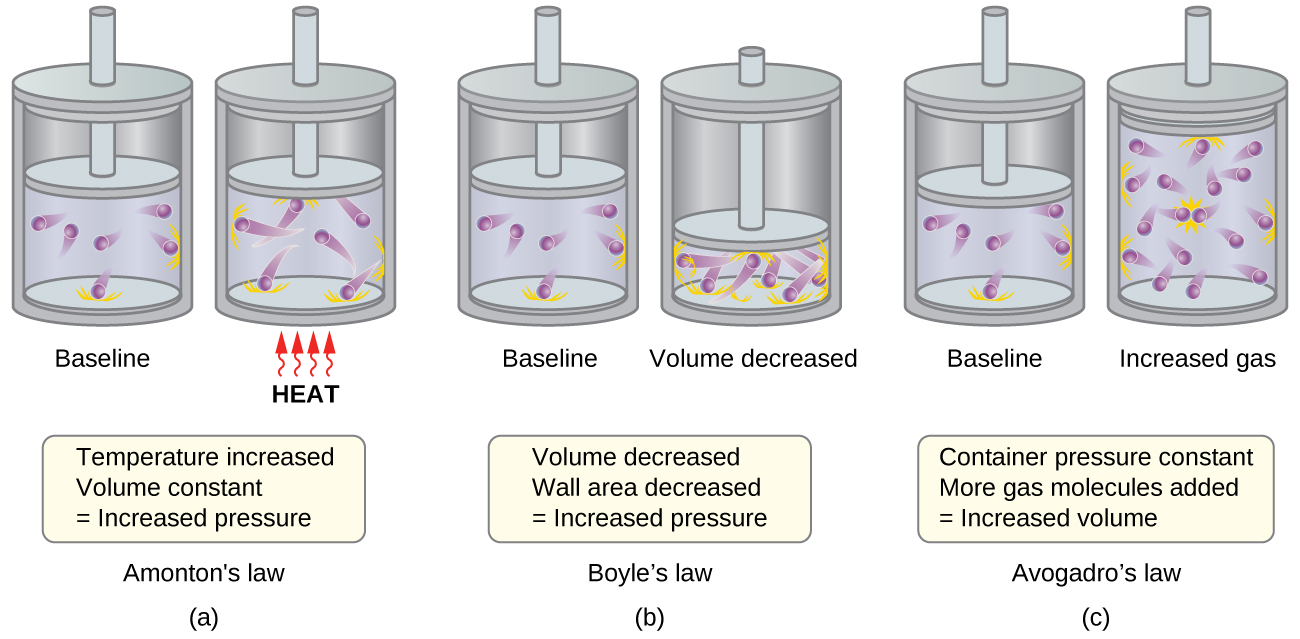
• Lei de Amontons. Se a temperatura for aumentada, a velocidade média e a energia cinética das moléculas de gás aumentam. Se o volume for mantido constante, o aumento da velocidade das moléculas de gás resulta em colisões mais frequentes e mais fortes com as paredes do recipiente, aumentando assim a pressão (Figura\(\PageIndex{1a}\)).
• A lei de Charles. Se a temperatura de um gás for aumentada, uma pressão constante só pode ser mantida se o volume ocupado pelo gás aumentar. Isso resultará em maiores distâncias médias percorridas pelas moléculas para alcançar as paredes do recipiente, bem como em uma maior área de superfície da parede. Essas condições diminuirão a frequência das colisões da parede molecular e o número de colisões por unidade de área, cujos efeitos combinados equilibram o efeito do aumento das forças de colisão devido à maior energia cinética na temperatura mais alta.
• Lei de Boyle. Se o volume do gás diminuir, a área da parede do recipiente diminui e a frequência de colisão da parede da molécula aumenta, o que aumenta a pressão exercida pelo gás (Figura\(\PageIndex{1b}\)).
• Lei de Avogadro. Em pressão e temperatura constantes, a frequência e a força das colisões da parede molecular são constantes. Sob tais condições, aumentar o número de moléculas gasosas exigirá um aumento proporcional no volume do recipiente para reduzir o número de colisões por unidade de área para compensar o aumento da frequência de colisões (Figura\(\PageIndex{1c}\)).
• Lei de Dalton. Devido às grandes distâncias entre eles, as moléculas de um gás em uma mistura bombardeiam as paredes do recipiente com a mesma frequência, independentemente de outros gases estarem presentes ou não, e a pressão total de uma mistura gasosa é igual à soma das pressões (parciais) dos gases individuais.

Figura\(\PageIndex{1}\): (a) Quando a temperatura do gás aumenta, a pressão do gás aumenta devido ao aumento da força e frequência das colisões moleculares. (b) Quando o volume diminui, a pressão do gás aumenta devido ao aumento da frequência de colisões moleculares. (c) Quando a quantidade de gás aumenta a uma pressão constante, o volume aumenta para produzir um número constante de colisões por unidade de área de parede por unidade de tempo.

Esta figura mostra 3 pares de pistões e cilindros. Em uma, que é chamada de “Lei de Charles”, o pistão é posicionado para o primeiro cilindro de forma que pouco mais da metade do volume disponível contenha 6 esferas roxas com trilhas atrás delas. As trilhas indicam movimento. Traços alaranjados se estendem da superfície interna do cilindro, onde as esferas colidiram. Esse cilindro é rotulado como “Linha de base”. No segundo cilindro, o pistão está na mesma posição e a etiqueta “Calor” é indicada em texto em letras maiúsculas em vermelho. Quatro flechas vermelhas com hastes onduladas estão apontando para cima, em direção à base do cilindro. As seis esferas roxas têm trilhas mais longas atrás delas e o número de traços alaranjados indicando pontos de colisão com as paredes do contêiner aumentou. Um retângulo abaixo do diagrama afirma: “Temperatura aumentada, constante de volume é igual a aumento de pressão”. Em b, que é rotulado como “Lei de Boyle”, o primeiro cilindro de linha de base mostrado é idêntico ao primeiro cilindro de a. No segundo cilindro, o pistão foi movido, diminuindo o volume disponível para as 6 esferas roxas para metade do volume inicial. As seis esferas roxas têm trilhas mais longas atrás delas e o número de traços alaranjados indicando pontos de colisão com as paredes do contêiner aumentou. Esse segundo cilindro é rotulado como “Diminuição do volume”. Um retângulo abaixo do diagrama afirma: “O volume diminuiu, a área da parede diminuída é igual ao aumento da pressão”. Em c, que é chamada de “Lei de Avogadro”, o primeiro cilindro de linha de base mostrado é idêntico ao primeiro cilindro de a. No segundo cilindro, o número de esferas roxas mudou de 6 para 12 e o volume dobrou. Esse segundo cilindro é rotulado como “Aumento de gás”. Um retângulo abaixo do diagrama afirma: “Em pressão constante, mais moléculas de gás adicionadas são iguais a aumento de volume”.

Velocidades moleculares e energia cinética

A discussão anterior mostrou que o KMT explica qualitativamente os comportamentos descritos pelas várias leis do gás. Os postulados dessa teoria podem ser aplicados de uma forma mais quantitativa para derivar essas leis individuais. Para fazer isso, devemos primeiro observar as velocidades e energias cinéticas das moléculas de gás e a temperatura de uma amostra de gás.

Em uma amostra de gás, moléculas individuais têm velocidades amplamente variadas; no entanto, devido ao grande número de moléculas e colisões envolvidas, a distribuição da velocidade molecular e a velocidade média são constantes. Essa distribuição de velocidade molecular é conhecida como distribuição Maxwell-Boltzmann e representa o número relativo de moléculas em uma amostra a granel de gás que possui uma determinada velocidade (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): A distribuição da velocidade molecular do gás oxigênio a 300 K é mostrada aqui. Muito poucas moléculas se movem em velocidades muito baixas ou muito altas. O número de moléculas com velocidades intermediárias aumenta rapidamente até o máximo, que é a velocidade mais provável, e depois cai rapidamente. Observe que a velocidade mais provável, ¾ _p, é um pouco menor que 400 m/s, enquanto a velocidade quadrada média raiz, u _rms, está mais próxima de 500 m/s.

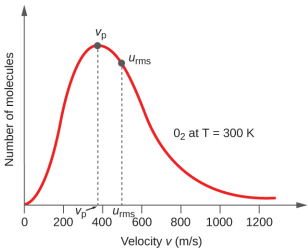
A energia cinética (KE) de uma partícula de massa (m) e velocidade (u) é dada por:

\[\ce{KE}=\dfrac{1}{2}mu^2 \nonumber \]

Expressar massa em quilogramas e velocidade em metros por segundo produzirá valores de energia em unidades de joules (J = kg m ² s ^—2). Para lidar com um grande número de moléculas de gás, usamos médias de velocidade e energia cinética. No KMT, a raiz da velocidade quadrada média de uma partícula, u _rms, é definida como a raiz quadrada da média dos quadrados das velocidades com n = o número de partículas:

\[u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}} \nonumber \]

A energia cinética média, KE _avg, é então igual a:

\[\mathrm{KE_{avg}}=\dfrac{1}{2}mu^2_\ce{rms} \nonumber \]

A _média KE de uma coleção de moléculas de gás também é diretamente proporcional à temperatura do gás e pode ser descrita pela equação:

\[\mathrm{KE_{avg}}=\dfrac{3}{2}RT \nonumber \]

onde R é a constante do gás e T é a temperatura kelvin. Quando usada nessa equação, a forma apropriada da constante do gás é 8,314 J mol ^-1 K ^-1 (8,314 kg m ² s ^{— 2} mol ^-1 K ^—1). Essas duas equações separadas para a _média KE podem ser combinadas e reorganizadas para produzir uma relação entre velocidade molecular e temperatura:

\[\dfrac{1}{2}mu^2_\ce{rms}=\dfrac{3}{2}RT \nonumber \]

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \label{RMS} \]

Exemplo\(\PageIndex{1}\): Calculation of u_rms

Calcule a velocidade quadrada média de uma molécula de nitrogênio a 30 °C.

Solução

Converta a temperatura em Kelvin:

\[30°C+273=303\: K \nonumber \]

Determine a massa de uma molécula de nitrogênio em quilogramas:

\[\mathrm{\dfrac{28.0\cancel{g}}{1\: mol}×\dfrac{1\: kg}{1000\cancel{g}}=0.028\:kg/mol} \nonumber \]

Substitua as variáveis e constantes na fórmula da velocidade quadrada média (Equação\ ref {RMS}), substituindo Joules pelo equivalente kg m ² s ^—2:

\[ \begin{align*} u_\ce{rms} &= \sqrt{\dfrac{3RT}{m}} \\ u_\ce{rms} &=\sqrt{\dfrac{3(8.314\:J/mol\: K)(303\: K)}{(0.028\:kg/mol)}} \\ &=\sqrt{2.70 \times 10^5\:m^2s^{−2}} \\ &= 519\:m/s \end{align*} \nonumber \]

Exercício\(\PageIndex{1}\)

Calcule a velocidade quadrada média de uma molécula de oxigênio a —23 °C.

Resposta

441 m/s

Se a temperatura de um gás aumenta, sua _média de KE aumenta, mais moléculas têm velocidades mais altas e menos moléculas têm velocidades mais baixas, e a distribuição muda para velocidades mais altas em geral, ou seja, para a direita. Se a temperatura diminuir, a _média KE diminui, mais moléculas têm velocidades mais baixas e menos moléculas têm velocidades mais altas, e a distribuição muda para velocidades mais baixas em geral, ou seja, para a esquerda. Esse comportamento é ilustrado para o gás nitrogênio na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): A distribuição da velocidade molecular do gás nitrogênio (N ₂) muda para a direita e se achata à medida que a temperatura aumenta; ela muda para a esquerda e aumenta à medida que a temperatura diminui.

Um gráfico com quatro curvas inclinadas positivamente ou à direita de alturas variadas é mostrado. O eixo horizontal é rotulado como “Velocidade v (m dividida por s)”. Esse eixo é marcado por incrementos de 500 começando em 0 e se estendendo até 1500. O eixo vertical é rotulado como “Fração de moléculas”. O rótulo “N subscrito 2" aparece no espaço aberto na área superior direita do gráfico. A mais alta e mais estreita dessas curvas é rotulada como “100 K”. Sua extremidade direita parece tocar o eixo horizontal em torno de 700 m por s. É seguida por uma curva um pouco mais larga chamada “200 K”, que é cerca de três quartos da altura da curva inicial. Sua extremidade direita parece tocar o eixo horizontal em torno de 850 m por s. A terceira curva é significativamente mais larga e tem apenas cerca de metade da altura da curva inicial. É rotulado como “500 K.” Sua extremidade direita parece tocar o eixo horizontal em torno de 1450 m por s. A curva final tem apenas cerca de um terço da altura da curva inicial. É muito mais largo que os outros, tanto que sua extremidade direita ainda não atingiu o eixo horizontal. Essa curva é rotulada como “1000 K”.

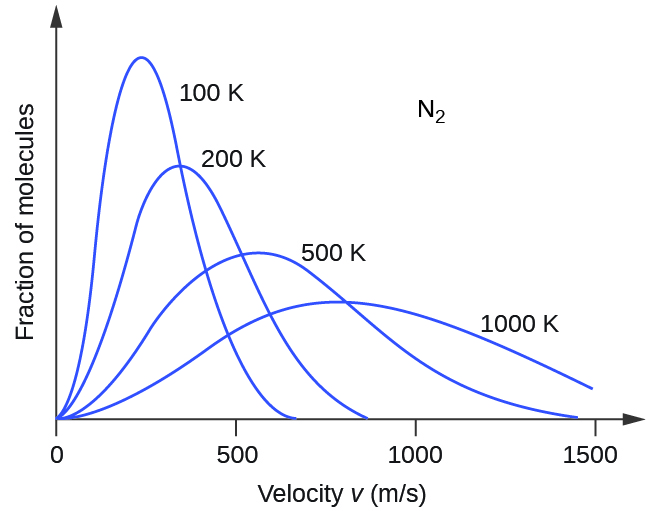
Em uma determinada temperatura, todos os gases têm a mesma _média de KE para suas moléculas. Gases compostos por moléculas mais leves têm mais partículas de alta velocidade e um u _rms mais alto, com uma distribuição de velocidade que atinge o pico em velocidades relativamente mais altas. Gases que consistem em moléculas mais pesadas têm mais partículas de baixa velocidade, u _rms mais baixos e uma distribuição de velocidade que atinge o pico em velocidades relativamente mais baixas. Essa tendência é demonstrada pelos dados de uma série de gases nobres mostrados na Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): A velocidade molecular está diretamente relacionada à massa molecular. Em uma determinada temperatura, moléculas mais leves se movem mais rápido, em média, do que moléculas mais pesadas.

Um gráfico é mostrado com quatro curvas inclinadas positivamente ou à direita de alturas variadas. O eixo horizontal é rotulado como “Velocidade v (m dividida por s)”. Esse eixo é marcado por incrementos de 500 começando em 0 e se estendendo até 3000. O eixo vertical é rotulado como “Fração de moléculas”. A mais alta e mais estreita dessas curvas é rotulada como “X e”. Sua extremidade direita parece tocar o eixo horizontal em torno de 600 m por s. É seguida por uma curva um pouco mais larga chamada “A r”, que tem cerca de metade da altura da curva inicial. Sua extremidade direita parece tocar o eixo horizontal em torno de 900 m por s. A terceira curva é significativamente mais larga e pouco mais de um terço da altura da curva inicial. É rotulado como “N e”. Sua extremidade direita parece tocar o eixo horizontal em torno de 1200 m por s. A curva final tem apenas cerca de um quarto da altura da curva inicial. É muito mais largo que os outros, tanto que sua direita atinge o eixo horizontal em torno de 2500 m por s. Essa curva é rotulada como “H e”.

O simulador de gás pode ser usado para examinar o efeito da temperatura nas velocidades moleculares. Examine os “histogramas de energia” (distribuições de velocidade molecular) e as “informações de espécies” do simulador (que fornecem valores médios de velocidade) para moléculas de diferentes massas em várias temperaturas.

A teoria cinético-molecular explica o comportamento dos gases, parte II

De acordo com a lei de Graham, as moléculas de um gás estão em movimento rápido e as próprias moléculas são pequenas. A distância média entre as moléculas de um gás é grande em comparação com o tamanho das moléculas. Como consequência, as moléculas de gás podem se mover umas sobre as outras facilmente e se difundir a taxas relativamente rápidas.

A taxa de efusão de um gás depende diretamente da velocidade (média) de suas moléculas:

\[\textrm{effusion rate} ∝ u_\ce{rms} \nonumber \]

Usando essa relação e a equação que relaciona a velocidade molecular à massa, a lei de Graham pode ser facilmente derivada conforme mostrado aqui:

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \nonumber \]

\[m=\dfrac{3RT}{u^2_\ce{rms}}=\dfrac{3RT}{\overline{u}^2} \nonumber \]

\[\mathrm{\dfrac{effusion\: rate\: A}{effusion\: rate\: B}}=\dfrac{u_\mathrm{rms\:A}}{u_\mathrm{rms\:B}}=\dfrac{\sqrt{\dfrac{3RT}{m_\ce{A}}}}{\sqrt{\dfrac{3RT}{m_\ce{B}}}}=\sqrt{\dfrac{m_\ce{B}}{m_\ce{A}}} \nonumber \]

A razão das taxas de efusão é, portanto, derivada para ser inversamente proporcional à proporção das raízes quadradas de suas massas. Essa é a mesma relação observada experimentalmente e expressa como a lei de Graham.

Resumo

A teoria molecular cinética é um modelo simples, mas muito eficaz, que explica efetivamente o comportamento ideal do gás. A teoria pressupõe que os gases consistem em moléculas amplamente separadas de volume insignificante que estão em constante movimento, colidindo elasticamente umas com as outras e as paredes de seu recipiente com velocidades médias determinadas por suas temperaturas absolutas. As moléculas individuais de um gás exibem uma faixa de velocidades, sendo a distribuição dessas velocidades dependente da temperatura do gás e da massa de suas moléculas.

Equações-chave

• \(u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}}\)
• \(\mathrm{KE_{avg}}=\dfrac{3}{2}RT\)
• \(u_\ce{rms}=\sqrt{\dfrac{3RT}{m}}\)

Resumo

teoria molecular cinética

teoria baseada em princípios e suposições simples que efetivamente explica o comportamento ideal do gás

velocidade quadrada média (u _rms)

medida da velocidade média para um grupo de partículas calculada como a raiz quadrada da velocidade média quadrada