9.4: Efusão e difusão de gases

Last updated
Save as PDF

Page ID: 185458

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

⇨

Objetivos de

Definir e explicar efusão e difusão
Declare a lei de Graham e use-a para calcular propriedades relevantes do gás

Se você já esteve em uma sala quando uma pizza bem quente foi entregue, ficou ciente do fato de que moléculas gasosas podem se espalhar rapidamente por uma sala, como evidenciado pelo aroma agradável que logo chega ao nariz. Embora as moléculas gasosas viajem a velocidades tremendas (centenas de metros por segundo), elas colidem com outras moléculas gasosas e viajam em muitas direções diferentes antes de atingir o alvo desejado. Em temperatura ambiente, uma molécula gasosa sofrerá bilhões de colisões por segundo. O caminho livre médio é a distância média que uma molécula percorre entre as colisões. O caminho livre médio aumenta com a diminuição da pressão; em geral, o caminho livre médio para uma molécula gasosa será centenas de vezes o diâmetro da molécula

Em geral, sabemos que quando uma amostra de gás é introduzida em uma parte de um recipiente fechado, suas moléculas se dispersam muito rapidamente pelo recipiente; esse processo pelo qual as moléculas se dispersam no espaço em resposta às diferenças de concentração é chamado de difusão (mostrado na Figura\(\PageIndex{1}\)) . Os átomos ou moléculas gasosas, é claro, desconhecem qualquer gradiente de concentração, eles simplesmente se movem aleatoriamente - regiões de maior concentração têm mais partículas do que regiões de concentrações mais baixas e, portanto, ocorre um movimento líquido de espécies de áreas de alta para baixa concentração. Em um ambiente fechado, a difusão acabará resultando em concentrações iguais de gás por toda parte, conforme mostrado na Figura\(\PageIndex{1}\). Os átomos e moléculas gasosos continuam se movendo, mas como suas concentrações são as mesmas em ambos os bulbos, as taxas de transferência entre os bulbos são iguais (nenhuma transferência líquida de moléculas ocorre).

Figura\(\PageIndex{1}\): (a) Dois gases, H ₂ e O ₂, são inicialmente separados. (b) Quando a torneira é aberta, elas se misturam. O gás mais leve, H ₂, passa pela abertura mais rápido do que O ₂, então, logo após a abertura da torneira, mais moléculas de H ₂ se movem para o lado O ₂ do que moléculas de O ₂ se movem para o lado H ₂. (c) Após um curto período de tempo, tanto as moléculas de O ₂ de movimento mais lento quanto as moléculas de H ₂ de movimento mais rápido se distribuíram uniformemente em ambos os lados do vaso.

Muitas vezes estamos interessados na taxa de difusão, na quantidade de gás que passa por alguma área por unidade de tempo:

\[\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}} \nonumber \]

A taxa de difusão depende de vários fatores: o gradiente de concentração (o aumento ou diminuição da concentração de um ponto a outro); a quantidade de área de superfície disponível para difusão; e a distância que as partículas de gás devem percorrer. Observe também que o tempo necessário para que a difusão ocorra é inversamente proporcional à taxa de difusão, conforme mostrado na equação da taxa de difusão.

Um processo que envolve o movimento de espécies gasosas semelhante à difusão é o derrame, a fuga de moléculas de gás através de um pequeno orifício, como um orifício em um balão, para o vácuo (Figura\(\PageIndex{1}\)). Embora as taxas de difusão e efusão dependam da massa molar do gás envolvido, suas taxas não são iguais; no entanto, as proporções de suas taxas são as mesmas.

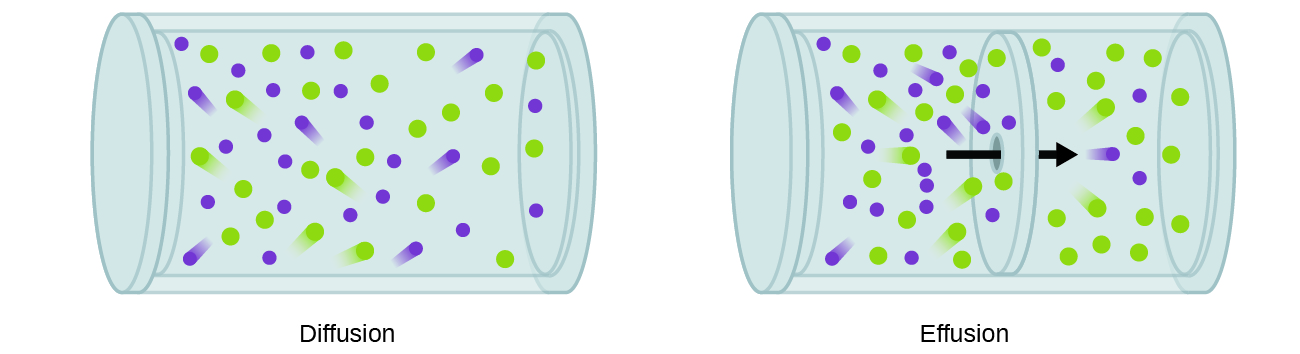
Figura\(\PageIndex{2}\): A difusão ocorre quando as moléculas de gás se dispersam por um recipiente. A efusão ocorre quando um gás passa por uma abertura menor que o caminho livre médio das partículas, ou seja, a distância média percorrida entre as colisões. Efetivamente, isso significa que apenas uma partícula passa por cada vez.

Se uma mistura de gases for colocada em um recipiente com paredes porosas, os gases fluem pelas pequenas aberturas nas paredes. Os gases mais leves passam pelas aberturas pequenas mais rapidamente (a uma taxa maior) do que os mais pesados (Figura\(\PageIndex{2}\)). Em 1832, Thomas Graham estudou as taxas de efusão de diferentes gases e formulou a lei de efusão de Graham: A taxa de efusão de um gás é inversamente proporcional à raiz quadrada da massa de suas partículas:

\[\textrm{rate of effusion}∝\dfrac{1}{\sqrt{ℳ}} \nonumber \]

Isso significa que se dois gases A e B estiverem na mesma temperatura e pressão, a razão de suas taxas de efusão é inversamente proporcional à proporção das raízes quadradas das massas de suas partículas:

\[\dfrac{\textrm{rate of effusion of B}}{\textrm{rate of effusion of A}}=\dfrac{\sqrt{ℳ_\ce{A}}}{\sqrt{ℳ_\ce{B}}} \nonumber \]

Figura\(\PageIndex{3}\): Um balão cheio de ar (o azul) permanece cheio durante a noite. Um balão cheio de hélio (o verde) esvazia parcialmente porque os átomos menores e leves de hélio se espalham por pequenos orifícios na borracha com muito mais facilidade do que as moléculas mais pesadas de nitrogênio e oxigênio encontradas no ar. (crédito: modificação do trabalho de Mark Ott)

Exemplo\(\PageIndex{1}\): Applying Graham’s Law to Rates of Effusion

Calcule a razão entre a taxa de efusão de hidrogênio e a taxa de efusão de oxigênio.

Solução

Da lei de Graham, temos:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{\sqrt{1.43\cancel{g\: L^{−1}}}}{\sqrt{0.0899\cancel{g\: L^{−1}}}}=\dfrac{1.20}{0.300}=\dfrac{4}{1}} \nonumber \]

Usando massas molares:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{32\cancel{g\: mol^{−1}}}{2\cancel{g\: mol^{−1}}}=\dfrac{\sqrt{16}}{\sqrt{1}}=\dfrac{4}{1}} \nonumber \]

O hidrogênio é liberado quatro vezes mais rápido que o oxigênio.

Exercício\(\PageIndex{1}\)

Em uma pressão e temperatura específicas, o gás nitrogênio é liberado à taxa de 79 mL/s. Usando o mesmo aparelho na mesma temperatura e pressão, em que taxa o dióxido de enxofre será expelido?

Responda: 52 mL/s

Aqui está outro exemplo, explicando como determinar os tempos difere da determinação das taxas.

Exemplo\(\PageIndex{2}\): Effusion Time Calculations

São necessários 243 s para que 4,46 × 10 ⁻⁵ mol Xe escorra por um pequeno orifício. Sob as mesmas condições, quanto tempo demorará 4,46 × 10 ⁻⁵ mol Ne para efusar?

Solução

É importante resistir à tentação de usar os tempos diretamente e lembrar como a taxa se relaciona com o tempo e como ela se relaciona com a massa. Lembre-se da definição de taxa de efusão:

\[\textrm{rate of effusion}=\dfrac{\textrm{amount of gas transferred}}{\textrm{time}}\nonumber \]

e combine-a com a lei de Graham:

\[\dfrac{\textrm{rate of effusion of gas Xe}}{\textrm{rate of effusion of gas Ne}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Para obter:

\[\dfrac{\dfrac{\textrm{amount of Xe transferred}}{\textrm{time for Xe}}}{\dfrac{\textrm{amount of Ne transferred}}{\textrm{time for Ne}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Observando essa quantidade de A = quantidade de B e resolvendo o tempo para Ne:

\[\dfrac{\dfrac{\cancel{\textrm{amount of Xe}}}{\textrm{time for Xe}}}{\dfrac{\cancel{\textrm{amount of Ne}}}{\textrm{time for Ne}}}=\dfrac{\textrm{time for Ne}}{\textrm{time for Xe}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}} \nonumber \]

e valores substitutos:

\[\mathrm{\dfrac{time\: for\: Ne}{243\:s}=\sqrt{\dfrac{20.2\cancel{g\: mol}}{131.3\cancel{g\: mol}}}=0.392}\nonumber \]

Por fim, resolva a quantidade desejada:

\[\mathrm{time\: for\: Ne=0.392×243\:s=95.3\:s}\nonumber \]

Observe que esta resposta é razoável: Como Ne é mais leve que Xe, a taxa de efusão para Ne será maior do que aquela para\(\ce{Xe}\), o que significa que o tempo de efusão para Ne será menor do que para Xe.

Exercício\(\PageIndex{2}\)

Um balão de festa cheio de hélio esvazia até\(\dfrac{2}{3}\) seu volume original em 8,0 horas. Quanto tempo demorará um balão idêntico cheio com o mesmo número de moles de ar (= 28,2 g/mol) para esvaziar até\(\dfrac{1}{2}\) o volume original?

Responda: 32 h

Finalmente, aqui está mais um exemplo que mostra como calcular a massa molar a partir de dados da taxa de efusão.

Exemplo\(\PageIndex{3}\): Determining Molar Mass Using Graham’s Law

Um gás desconhecido é eliminado 1,66 vezes mais rapidamente do que o CO ₂. Qual é a massa molar do gás desconhecido? Você pode fazer uma suposição razoável sobre sua identidade?

Solução

Da lei de Graham, temos:

\[\mathrm{\dfrac{rate\: of\: effusion\: of\: Unknown}{rate\: of\: effusion\: of\: CO_2}}=\dfrac{\sqrt{ℳ_\mathrm{CO_2}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Conecte dados conhecidos:

\[\dfrac{1.66}{1}=\dfrac{\sqrt{44.0\:\ce{g/mol}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Resolver:

\[ℳ_{Unknown}=\mathrm{\dfrac{44.0\:g/mol}{(1.66)^2}=16.0\:g/mol} \nonumber \]

O gás poderia muito bem ser CH ₄, o único gás com essa massa molar.

Exercício

O gás hidrogênio é liberado por um recipiente poroso 8,97 vezes mais rápido do que um gás desconhecido. Estime a massa molar do gás desconhecido.

Responda: 163 g/mol

Aplicação: Uso de difusão para enriquecimento de urânio

A difusão gasosa tem sido usada para produzir urânio enriquecido para uso em usinas nucleares e armas. O urânio natural contém apenas 0,72% de ²³⁵ U, o tipo de urânio que é “fóssil”, ou seja, capaz de sustentar uma reação em cadeia de fissão nuclear. Os reatores nucleares precisam de combustível de 2 a 5% ²³⁵ U, e as bombas nucleares precisam de concentrações ainda maiores. Uma forma de enriquecer o urânio até os níveis desejados é aproveitar a lei de Graham. Em uma planta de enriquecimento por difusão gasosa, o hexafluoreto de urânio (UF ₆, o único composto de urânio volátil o suficiente para funcionar) é bombeado lentamente através de grandes vasos cilíndricos chamados difusores, que contêm barreiras porosas com aberturas microscópicas. O processo é de difusão porque o outro lado da barreira não é evacuado. As ²³⁵ moléculas de UF ₆ têm uma velocidade média mais alta e se difundem pela barreira um pouco mais rápido do que as ²³⁸ moléculas UF ₆ mais pesadas. O gás que passou pela barreira é ligeiramente enriquecido em ²³⁵ UF ₆ e o gás residual está ligeiramente esgotado. A pequena diferença nos pesos moleculares entre ²³⁵ UF ₆ e ²³⁸ UF ₆, apenas cerca de 0,4% de enriquecimento, é alcançada em um difusor (Figura\(\PageIndex{4}\)). Mas ao conectar muitos difusores em uma sequência de estágios (chamada de cascata), o nível de enriquecimento desejado pode ser alcançado.

Figura\(\PageIndex{4}\): Em um difusor, o UF ₆ gasoso é bombeado através de uma barreira porosa, que separa parcialmente ²³⁵ UF ₆ de ²³⁸ UF ₆. O UF ₆ deve passar por muitas unidades difusoras grandes para obter enriquecimento suficiente em ²³⁵U.

A separação em grande escala dos gases ²³⁵ UF ₆ dos ²³⁸ UF ₆ foi feita pela primeira vez durante a Segunda Guerra Mundial, na instalação de energia atômica em Oak Ridge, Tennessee, como parte do Projeto Manhattan (o desenvolvimento da primeira bomba atômica). Embora a teoria seja simples, isso exigiu superar muitos desafios técnicos assustadores para fazê-la funcionar na prática. A barreira deve ter orifícios minúsculos e uniformes (cerca de 10 a ⁶ cm de diâmetro) e ser porosa o suficiente para produzir altas taxas de fluxo. Todos os materiais (barreira, tubulação, revestimentos de superfície, lubrificantes e juntas) precisam ser capazes de conter, mas não reagir com, o UF ₆ altamente reativo e corrosivo.

Como as usinas de difusão gasosa requerem quantidades muito grandes de energia (para comprimir o gás até as altas pressões necessárias e conduzi-lo pela cascata do difusor, para remover o calor produzido durante a compressão, etc.), ele agora está sendo substituído pela tecnologia de centrífuga a gás, que requer muito menos energia. Uma questão política atual é como negar essa tecnologia ao Irã, para evitar que ele produza urânio enriquecido suficiente para ser usado na fabricação de armas nucleares.

Resumo

Átomos e moléculas gasosas se movem livre e aleatoriamente pelo espaço. A difusão é o processo pelo qual átomos e moléculas gasosas são transferidos de regiões de concentração relativamente alta para regiões de concentração relativamente baixa. A efusão é um processo similar no qual espécies gasosas passam de um recipiente para o vácuo através de orifícios muito pequenos. As taxas de efusão de gases são inversamente proporcionais às raízes quadradas de suas densidades ou às raízes quadradas das massas de seus átomos/moléculas (lei de Graham).

Equações-chave

\(\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}}\)
\(\dfrac{\textrm{rate of effusion of gas A}}{\textrm{rate of effusion of gas B}}=\dfrac{\sqrt{m_B}}{\sqrt{m_A}}=\dfrac{\sqrt{ℳ_B}}{\sqrt{ℳ_A}}\)

Resumo

difusão: movimento de um átomo ou molécula de uma região de concentração relativamente alta para uma de concentração relativamente baixa (discutido neste capítulo com relação a espécies gasosas, mas aplicável a espécies em qualquer fase)

efusão: transferência de átomos ou moléculas gasosas de um recipiente para o vácuo através de aberturas muito pequenas

Lei da efusão de Graham: as taxas de difusão e efusão de gases são inversamente proporcionais às raízes quadradas de suas massas moleculares

significa caminho livre: distância média que uma molécula percorre entre colisões

taxa de difusão: quantidade de gás difundindo por uma determinada área ao longo de um determinado tempo