13.R: Funções trigonométricas (Revisão)

Last updated
Save as PDF

Page ID: 189238

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

5.1: Exercícios de revisão

Para os exercícios 1-2, converta as medidas do ângulo em graus.

1)$\dfrac{π}{4}$

Responda: $45°$

2)$−\dfrac{5π}{3}$

Para os exercícios 3-6, converta as medidas do ângulo em radianos.

3)$-210°$

Responda: $−\dfrac{7π}{6}$

4)$180°$

5) Encontre o comprimento de um arco em um círculo de$7$ metros de raio subtendido pelo ângulo central de$85°$.

Responda: $10.385$metros

6) Encontre a área do setor de um círculo com$32$ pés de diâmetro e um ângulo de$\dfrac{3π}{5}$ radianos.

Para os exercícios 7-8, determine o ângulo entre$0°$ e$360°$ que é coterminal com o ângulo dado.

7)$420°$

Responda: $60°$

8)$−80°$

Para os exercícios 9-10, determine o ângulo entre$0$ e$2π$ em radianos que é coterminal com o ângulo dado.

9)$− \dfrac{20π}{11}$

Responda: $\dfrac{2π}{11}$

10)$\dfrac{14π}{5}$

Para os exercícios 11-, desenhe o ângulo fornecido na posição padrão no plano cartesiano.

11)$-210°$

Responda: $alt$

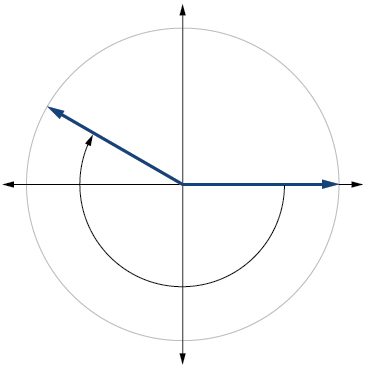
12)$75°$

13)$\dfrac{5π}{4}$

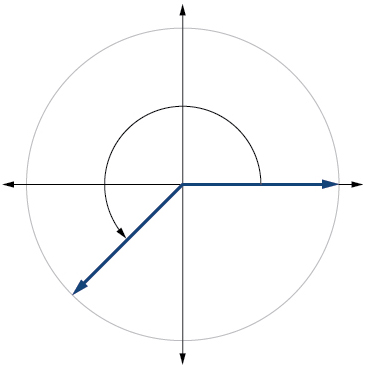
Responda: $CNX_Precalc_Figure_05_04_219.jpg$

14)$−\dfrac{π}{3}$

15) Encontre a velocidade linear de um ponto no equador da Terra se a Terra tiver um raio de$3,960$ milhas e a Terra girar em seu eixo a cada$24$ hora. Resposta expressa em milhas por hora.

Resposta: $1036.73$milhas por hora

16) Uma roda de carro com um diâmetro de$18$ polegadas gira na taxa de$10$ rotações por segundo. Qual é a velocidade do carro em milhas por hora?

5.2: Exercícios de revisão

1) Encontre o valor exato de$ \sin \dfrac{π}{3}$.

Responda: $\dfrac{\sqrt{3}}{2}$

2) Encontre o valor exato de$ \cos \dfrac{π}{4}$.

3) Encontre o valor exato de$ \cos π $.

Responda: $-1$

4) Indique o ângulo de referência para$300°$.

5) Indique o ângulo de referência para$ \dfrac{3π}{4}$.

Responda: $ \dfrac{π}{4}$

6) Calcule o cosseno de$330°$.

7) Calcule um seno de$\dfrac{5π}{4}$.

Responda: $−\dfrac{\sqrt{2}}{2}$

8) Declare o domínio das funções seno e cosseno.

9) Indique o intervalo das funções seno e cosseno.

Responda: $[–1,1]$

5.3: Exercícios de revisão

Para os exercícios 1-4, encontre o valor exato da expressão dada.

1)$ \cos \dfrac{π}{6} $

2)$ \tan \dfrac{π}{4} $

Responda: $1$

3)$ \csc \dfrac{π}{3}$

4)$ \sec \dfrac{π}{4} $

Responda: $\sqrt{2}$

Para os exercícios 4-12, use ângulos de referência para avaliar a expressão dada.

5)$ \sec \dfrac{11π}{3}$

6)$ \sec 315°$

Responda: $ \sqrt{2}$

7) Se$ \sec (t)=−2.5$, qual é o$ \sec (−t)$?

8) Se$ \tan (t)=−0.6 $, qual é o$ \tan (−t)$?

Responda: $0.6$

9) Se$ \tan (t)=\dfrac{1}{3}$, encontre$ \tan (t−π)$.

10) Se$ \cos (t)= \dfrac{\sqrt{2}}{2}$, encontre$ \sin (t+2π)$.

Responda: $\dfrac{\sqrt{2}}{2}$ou$−\dfrac{\sqrt{2}}{2}$

11) Quais funções trigonométricas são pares?

12) Quais funções trigonométricas são ímpares?

Responda: seno, cossecante, tangente, cotangente

5.4: Exercícios de revisão

Para os exercícios 1-5, use comprimentos laterais para avaliar.

1)$ \cos \dfrac{π}{4}$

2)$ \cot \dfrac{π}{3}$

Responda: $\dfrac{\sqrt{3}}{3}$

3)$ \tan \dfrac{π}{6}$

4)$ \cos (\dfrac{π}{2}) = \sin ( \_\_°)$

Responda: $0$

5)$ \csc (18°)= \sec (\_\_°)$

Para os exercícios 6-7, use as informações fornecidas para encontrar os comprimentos dos outros dois lados do triângulo reto.

6)$ \cos B= \dfrac{3}{5}, a=6$

Responda: $ b=8,c=10$

7)$ \tan A = \dfrac{5}{9},b=6 $

Para os exercícios 8-9, use a Figura abaixo para avaliar cada função trigonométrica.

$alt$

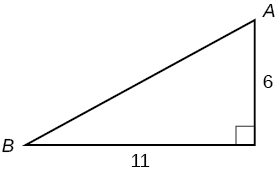
8)$ \sin A $

Responda: $ \dfrac{11\sqrt{157}}{157}$

9)$ \tan B $

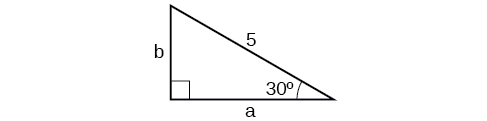
Para os exercícios 10-11, resolva os lados desconhecidos de um determinado triângulo.

10)

$alt$

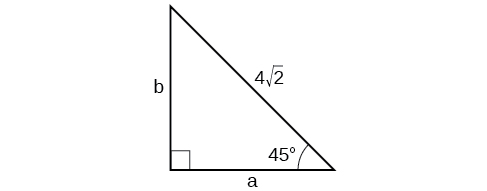
Responda: $a=4, b=4 $

11)

$alt$

12) Uma escada$15$ de pés se inclina contra um prédio de forma que o ângulo entre o solo e a escada seja$70°$. Qual a altura da escada até a lateral do prédio?

Responda: $14.0954$pés

13) O ângulo de elevação até o topo de um edifício em Baltimore é encontrado em$4$ graus do solo, a uma distância de um$1$ quilômetro da base do edifício. Usando essas informações, encontre a altura do prédio.

Teste prático

1) Converta$ \dfrac{5π}{6}$ radianos em graus.

Responda: $150°$

2)$−620°$ Converta em radianos.

3) Encontre o comprimento de um arco circular com um raio de$12$ centímetros subtendido pelo ângulo central de$30°$.

Responda: $6.283$centímetros

4) Encontre a área do setor com raio de$8$ pés e um ângulo de$\dfrac{5π}{4}$ radianos.

5) Encontre o ângulo entre$0°$ e$360°$ que é coterminal com$375°$.

Responda: $15°$

6) Encontre o ângulo entre$0$ e$2π$ em radianos que é coterminal com$−\dfrac{4π}{7}$.

7) Desenhe o ângulo$315°$ na posição padrão no plano cartesiano.

Responda: $alt$

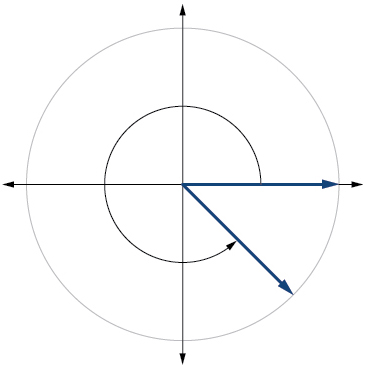
8) Desenhe o ângulo$−\dfrac{π}{6}$ na posição padrão no plano cartesiano.

9) Um carnaval tem uma roda gigante com um diâmetro de$80$ pés. O tempo para a roda gigante fazer uma revolução é de$75$ segundos. Qual é a velocidade linear em pés por segundo de um ponto na roda gigante? Qual é a velocidade angular em radianos por segundo?

Responda: $3.351$pés por segundo,$ \dfrac{2π}{75}$ radianos por segundo

10) Encontre o valor exato de$ \sin \dfrac{π}{6}$.

11) Calcule um seno de$240°$.

Responda: $−\dfrac{\sqrt{3}}{2}$

12) Declare o domínio das funções seno e cosseno.

13) Indique o intervalo das funções seno e cosseno.

Responda: $[ –1,1 ]$

14) Encontre o valor exato de$ \cot \dfrac{π}{4}$.

15) Encontre o valor exato de$ \tan \dfrac{π}{3}$.

Responda: $ \sqrt{3}$

16) Use ângulos de referência para avaliar$ \csc \dfrac{7π}{4}$.

17) Use ângulos de referência para avaliar$ \tan 210°$.

Responda: $\dfrac{\sqrt{3}}{3}$

18) Se$ \csc t=0.68$, qual é o$ \csc (−t)$?

19) Se$ \cos t= \dfrac{\sqrt{3}}{2}$, encontre$ \cos (t−2π)$.

Responda: $\dfrac{\sqrt{3}}{2}$

20) Quais funções trigonométricas são pares?

21) Encontre o ângulo que falta:$\cos \left(\dfrac{\pi }{6} \right)= \sin (\;)$

Responda: $\dfrac{π}{3}$

22) Encontre os lados faltantes do triângulo$ ABC: \sin B= \dfrac{3}{4},c=12$

23) Encontre os lados que faltam no triângulo.

$alt$

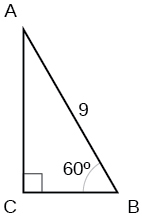
Responda: $a=\dfrac{9}{2},b=\dfrac{9\sqrt{3}}{2}$

24) O ângulo de elevação até o topo de um edifício em Chicago é encontrado em$9$ graus do solo, a uma distância de$2000$ pés da base do edifício. Usando essas informações, encontre a altura do prédio.