13.E: Funções trigonométricas (exercícios)

5.1: Ângulos

Nesta seção, examinaremos as propriedades dos ângulos.

Verbal

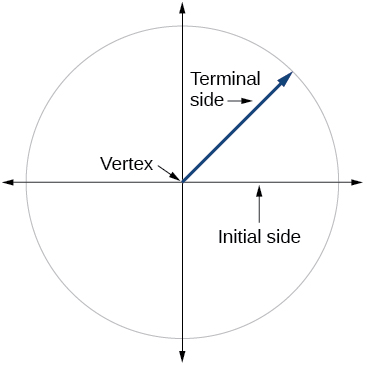
1) Desenhe um ângulo na posição padrão. Identifique o vértice, o lado inicial e o lado terminal.

Resposta

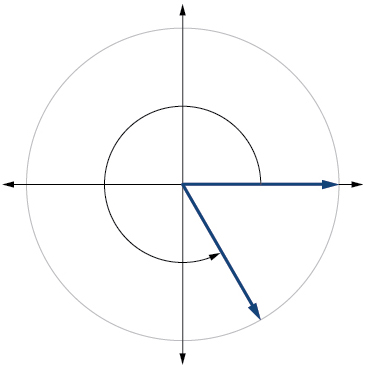
2) Explique por que há um número infinito de ângulos que são coterminais a um determinado ângulo.

3) Declare o que significa um ângulo positivo ou negativo e explique como desenhar cada um.

Resposta

Se o ângulo é positivo ou negativo determina a direção. Um ângulo positivo é desenhado no sentido anti-horário e um ângulo negativo é desenhado no sentido horário.

4) Como a medida radiana de um ângulo se compara à medida do grau? Inclua uma explicação dos\(1\) radianos em seu parágrafo.

5) Explique as diferenças entre a velocidade linear e a velocidade angular ao descrever o movimento ao longo de um caminho circular.

Responda

A velocidade linear é uma medida encontrada pelo cálculo da distância de um arco em comparação com o tempo. A velocidade angular é uma medida encontrada pelo cálculo do ângulo de um arco em comparação com o tempo.

Gráfica

Para os exercícios 6-21, desenhe um ângulo na posição padrão com a medida dada.

6)\(30^{\circ}\)

7)\(300^{\circ}\)

Responda

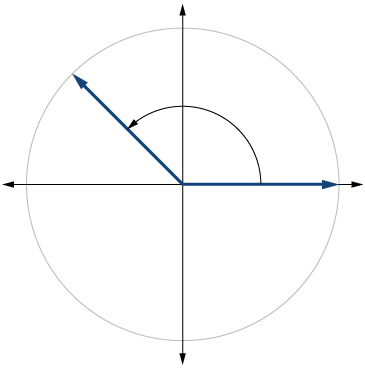
8)\(-80^{\circ}\)

9)\(135^{\circ}\)

Responda

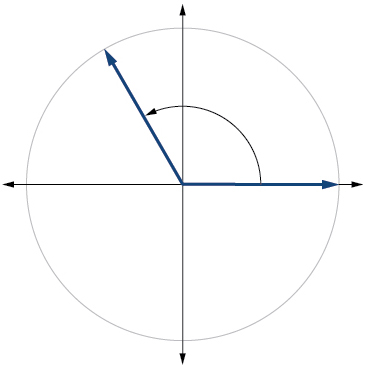
10)\(-150^{\circ}\)

11)\(\dfrac{2π}{3}\)

Responda

12)\(\dfrac{7π}{4}\)

13)\(\dfrac{5π}{6}\)

Responda

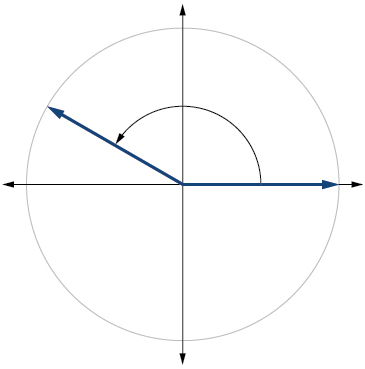
14)\(\dfrac{π}{2}\)

15)\(−\dfrac{π}{10}\)

Responda

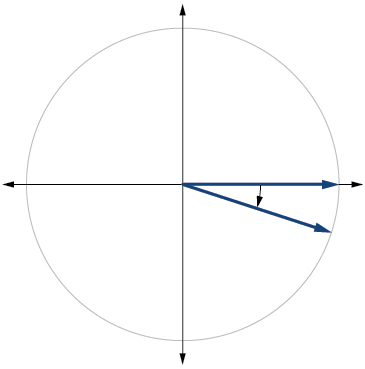
16)\(415^{\circ}\)

17)\(-120^{\circ}\)

Responda

\(240^{\circ}\)

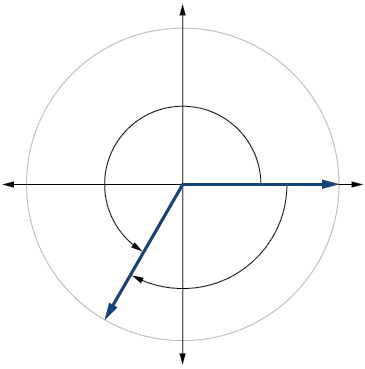
18)\(-315^{\circ}\)

19)\(\dfrac{22π}{3}\)

Responda

\(\dfrac{4π}{3}\)

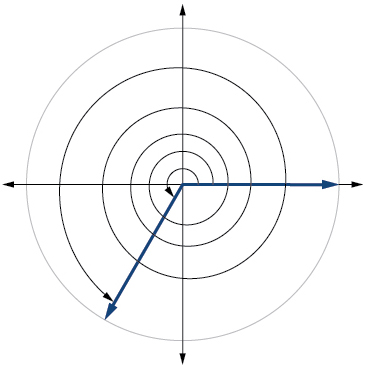
20)\(−\dfrac{π}{6}\)

21)\(−\dfrac{4π}{3}\)

Responda

\(\dfrac{2π}{3}\)

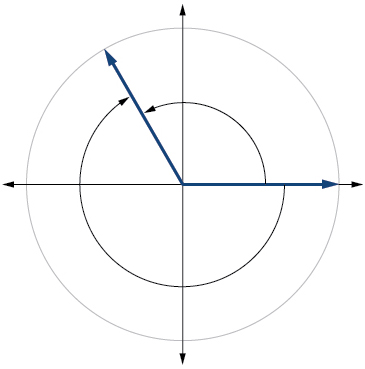
Para os exercícios 22-23, consulte a Figura abaixo. Arredonde para duas casas decimais.

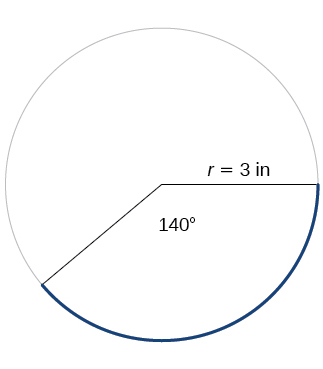
22) Encontre o comprimento do arco.

23) Encontre a área do setor.

Responda

\(\dfrac{27π}{2}≈11.00 \text{ in}^2\)

Para os exercícios 24-25, consulte a Figura abaixo. Arredonde para duas casas decimais.

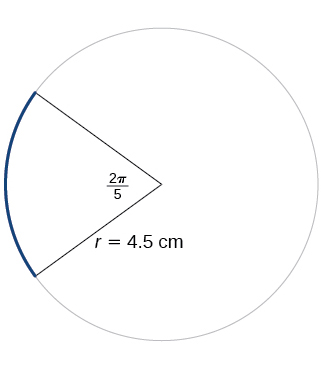
24) Encontre o comprimento do arco.

25) Encontre a área do setor.

Responda

\(\dfrac{81π}{20}≈12.72\text{ cm}^2\)

Algébrico

Para os exercícios 26-32, converta ângulos em radianos em graus.

26)\(\dfrac{3π}{4}\) radianos

27)\(\dfrac{π}{9}\) radianos

Responda

\(20^{\circ}\)

28)\(−\dfrac{5π}{4}\) radianos

29)\(\dfrac{π}{3}\) radianos

Responda

\(60^{\circ}\)

30)\(−\dfrac{7π}{3}\) radianos

31)\(−\dfrac{5π}{12}\) radianos

Responda

\(-75^{\circ}\)

32)\(\dfrac{11π}{6}\) radianos

Para os exercícios 33-39, converta ângulos em graus em radianos.

33)\(90^{\circ}\)

Responda

\(\dfrac{π}{2}\)radianos

34)\(100^{\circ}\)

(35)\(-540^{\circ}\)

Responda

\(−3π\)radianos

36)\(-120^{\circ}\)

37)\(180^{\circ}\)

Responda

\(π\)radianos

38)\(-315^{\circ}\)

39)\(150^{\circ}\)

Responda

\(\dfrac{5π}{6}\)radianos

Para os exercícios 40-45, use as informações fornecidas para encontrar o comprimento de um arco circular. Arredonde para duas casas decimais.

40) Encontre o comprimento do arco de um círculo de\(12\) polegadas de raio subtendido por um ângulo central de\(\dfrac{π}{4}\) radianos.

41) Encontre o comprimento do arco de um círculo de\(5.02\) milhas de raio subtendido pelo ângulo central de\(\dfrac{π}{3}\).

Responda

\(\dfrac{5.02π}{3}≈5.26\)milhas

42) Encontre o comprimento do arco de um círculo de\(14\) metros de diâmetro subtendido pelo ângulo central de\(\dfrac{5\pi }{6}\).

43) Encontre o comprimento do arco de um círculo de\(10\) centímetros de raio subtendido pelo ângulo central de\(50^{\circ}\).

Responda

\(\dfrac{25π}{9}≈8.73\)centímetros

44) Encontre o comprimento do arco de um círculo de\(5\) polegadas de raio subtendido pelo ângulo central de\(220^{circ}\).

45) Determine o comprimento do arco de um círculo de\(12\) metros de diâmetro subtendido pelo ângulo central é\(63^{circ}\).

Responda

\(\dfrac{21π}{10}≈6.60\)metros

Para os exercícios 46-49, use as informações fornecidas para encontrar a área do setor. Arredonde para quatro casas decimais.

46) Um setor de um círculo tem um ângulo central de\(45^{\circ}\) e um raio\(6\) cm.

47) Um setor de um círculo tem um ângulo central de\(30^{\circ}\) e um raio de\(20\) cm.

Responda

\(104.7198\; cm^2\)

48) Um setor de um círculo com\(10\) pés de diâmetro e um ângulo de\(\dfrac{π}{2}\) radianos.

49) Um setor de um círculo com raio de\(0.7\) polegadas e um ângulo de\(π\) radianos.

Responda

\(0.7697\; in^2\)

Para os exercícios 50-53, determine o ângulo entre\(0^{\circ}\) e\(360^{\circ}\) que é coterminal ao ângulo dado.

50)\(-40^{\circ}\)

51)\(-110^{\circ}\)

Responda

\(250^{\circ}\)

52)\(700^{\circ}\)

53)\(1400^{\circ}\)

Responda

\(320^{\circ}\)

Para os exercícios 54-57, determine o ângulo entre\(0\) e\(2\pi \) em radianos que é coterminal ao ângulo dado.

54)\(−\dfrac{π}{9}\)

55)\(\dfrac{10π}{3}\)

Responda

\(\dfrac{4π}{3}\)

(56)\(\dfrac{13π}{6}\)

57)\(\dfrac{44π}{9}\)

Responda

\(\dfrac{8π}{9}\)

Aplicativos do mundo real

58) Um caminhão com rodas de\(32\) -polegadas de diâmetro está viajando a\(60\) mi/h. Encontre a velocidade angular das rodas em rad/min. Quantas rotações por minuto as rodas fazem?

59) Uma bicicleta com rodas\(24\) de 5 polegadas de diâmetro está viajando a\(15\) mi/h. Encontre a velocidade angular das rodas em rad/min. Quantas rotações por minuto as rodas fazem?

Responda

\(1320\)\(210.085\)RPM de leitura

60) Uma roda de\(8\) polegadas de raio está girando\(15^{\circ}/s\). Qual é a velocidade linear\(v\), a velocidade angular em RPM e a velocidade angular em rad/s?

61) Uma roda de\(14\) polegadas de raio está girando\(0.5 \text{rad/s}\). Qual é a velocidade linear\(v\), a velocidade angular em RPM e a velocidade angular em graus/s?

Responda

\(7\)em. /s,\(4.77\) RPM,\(28.65\) graus/s

62) Um CD tem diâmetro de\(120\) milímetros. Ao reproduzir áudio, a velocidade angular varia para manter a velocidade linear constante onde o disco está sendo lido. Ao ler ao longo da borda externa do disco, a velocidade angular é de cerca de\(200\) RPM (rotações por minuto). Encontre a velocidade linear.

63) Ao ser gravado em uma unidade de CD-R gravável, a velocidade angular de um CD geralmente é muito mais rápida do que ao reproduzir áudio, mas a velocidade angular ainda varia para manter a velocidade linear constante onde o disco está sendo gravado. Ao escrever ao longo da borda externa do disco, a velocidade angular de uma unidade é de aproximadamente\(4800\) RPM (rotações por minuto). Determine a velocidade linear se o CD tiver um diâmetro de\(120\) milímetros.

Responda

\(1,809,557.37 \text{ mm/min}=30.16 \text{ m/s}\)

64) Uma pessoa está no equador da Terra (raio de\(3960\) milhas). Quais são suas velocidades lineares e angulares?

65) Encontre a distância ao longo de um arco na superfície da Terra que subtende um ângulo central de\(5\) minutos\((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). O raio da Terra é de\(3960\) milhas.

Responda

\(5.76\)milhas

66) Encontre a distância ao longo de um arco na superfície da Terra que subtende um ângulo central de\(7\) minutos\((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). O raio da Terra é de\(3960\) milhas.

67) Considere um relógio com um ponteiro das horas e dos minutos. Qual é a medida do ângulo que o ponteiro dos minutos traça em\(20\) minutos?

Responda

\(120°\)

Extensões

68) Duas cidades têm a mesma longitude. A latitude da cidade A é\(9.00\) graus norte e a latitude da cidade B é\(30.00\) grau norte. Suponha que o raio da Terra seja de\(3960\) milhas. Encontre a distância entre as duas cidades.

69) Uma cidade está localizada em\(40\) graus de latitude norte. Suponha que o raio da Terra seja de\(3960\) milhas e que a Terra gire uma vez a cada\(24\) hora. Encontre a velocidade linear de uma pessoa que reside nesta cidade.

Responda

\(794\)milhas por hora

70) Uma cidade está localizada em\(75\) graus de latitude norte. Suponha que o raio da Terra seja de\(3960\) milhas e que a Terra gire uma vez a cada\(24\) hora. Encontre a velocidade linear de uma pessoa que reside nesta cidade.

71) Encontre a velocidade linear da lua se a distância média entre a Terra e a lua for de\(239,000\) milhas, assumindo que a órbita da lua é circular e requer cerca de\(28\) dias. Resposta expressa em milhas por hora.

Responda

\(2,234\)milhas por hora

72) Uma bicicleta tem rodas em\(28\) polegadas de diâmetro. Um tacômetro determina que as rodas estão girando em\(180\) RPM (rotações por minuto). Descubra a velocidade em que a bicicleta está percorrendo a estrada.

73) Um carro viaja\(3\) milhas. Seus pneus fazem\(2640\) revoluções. Qual é o raio de um pneu em polegadas?

Responda

\(11.5\)polegadas

74) Uma roda em um trator tem um diâmetro\(24\) de -polegadas. Quantas rotações a roda faz se o trator viajar\(4\) quilômetros?

5.2: Círculo unitário - Funções de seno e cosseno

Verbal

1) Descreva o círculo unitário.

Responda

O círculo unitário é um círculo de raio\(1\) centrado na origem.

2) O que representam as\(y\) coordenadas\(x\) - e -dos pontos no círculo unitário?

3) Discuta a diferença entre um ângulo coterminal e um ângulo de referência.

Responda

Ângulos coterminais são ângulos que compartilham o mesmo lado terminal. Um ângulo de referência é o tamanho do menor ângulo agudo\(t\), formado pelo lado terminal do ângulo\(t\) e pelo eixo horizontal.

4) Explique como o cosseno de um ângulo no segundo quadrante difere do cosseno de seu ângulo de referência no círculo unitário.

5) Explique como o seno de um ângulo no segundo quadrante difere do seno de seu ângulo de referência no círculo unitário.

Responda

Os valores senoidais são iguais.

Algébrico

Para os exercícios 6-9, use o sinal dado das funções seno e cosseno para encontrar o quadrante no qual o ponto terminal determinado por\(t\) está.

6)\( \sin (t)<0\) e\( \cos (t)<0\)

7)\( \sin (t)>0\) e\( \cos (t)>0\)

Responda

\(\textrm{I}\)

8)\( \sin (t)>0 \) e\( \cos (t)<0\)

9)\( \sin (t)<0 \) e\( \cos (t)>0\)

Responda

\(\textrm{IV}\)

Para os exercícios 10-22, encontre o valor exato de cada função trigonométrica.

10)\(\sin \dfrac{π}{2}\)

11)\(\sin \dfrac{π}{3}\)

Responda

\(\dfrac{\sqrt{3}}{2}\)

12)\( \cos \dfrac{π}{2}\)

13)\( \cos \dfrac{π}{3}\)

Responda

\(\dfrac{1}{2}\)

14)\( \sin \dfrac{π}{4}\)

15)\( \cos \dfrac{π}{4}\)

Responda

\(\dfrac{\sqrt{2}}{2}\)

16)\( \sin \dfrac{π}{6}\)

17)\( \sin π\)

Responda

\(0\)

18)\( \sin \dfrac{3π}{2}\)

19)\( \cos π\)

Responda

\(−1\)

20)\( \cos 0\)

21)\(cos \dfrac{π}{6}\)

Responda

\(\dfrac{\sqrt{3}}{2}\)

22)\( \sin 0\)

Numérico

Para os exercícios 23-33, indique o ângulo de referência para o ângulo dado.

23)\(240°\)

Responda

\(60°\)

24)\(−170°\)

25)\(100°\)

Responda

\(80°\)

26)\(−315°\)

27)\(135°\)

Responda

\(45°\)

28)\(\dfrac{5π}{4}\)

29)\(\dfrac{2π}{3}\)

Responda

\(\dfrac{π}{3}\)

30)\(\dfrac{5π}{6}\)

31)\(−\dfrac{11π}{3}\)

Responda

\(\dfrac{π}{3}\)

32)\(\dfrac{−7π}{4}\)

33)\(\dfrac{−π}{8}\)

Responda

\(\dfrac{π}{8}\)

Para os exercícios 34-49, determine o ângulo de referência, o quadrante do lado terminal e o seno e o cosseno de cada ângulo. Se o ângulo não for um dos ângulos do círculo unitário, use uma calculadora e arredonde para três casas decimais.

34)\(225°\)

(35)\(300°\)

Responda

\(60°\), Quadrante IV,\( \sin (300°)=−\dfrac{\sqrt{3}}{2}, \cos (300°)=\dfrac{1}{2}\)

36)\(320°\)

37)\(135°\)

Responda

\(45°\), Quadrante II,\( \sin (135°)=\dfrac{\sqrt{2}}{2}, \cos (135°)=−\dfrac{\sqrt{2}}{2}\)

38)\(210°\)

39)\(120°\)

Responda

\(60°\), Quadrante II,\(\sin (120°)=\dfrac{\sqrt{3}}{2}\),\(\cos (120°)=−\dfrac{1}{2}\)

40)\(250°\)

41)\(150°\)

Responda

\(30°\), Quadrante II,\( \sin (150°)=\frac{1}{2}\),\(\cos(150°)=−\dfrac{\sqrt{3}}{2}\)

(42)\(\dfrac{5π}{4}\)

43)\(\dfrac{7π}{6}\)

Responda

\(\dfrac{π}{6}\), Quadrante III\(\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}\),\(\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}\)

44)\(\dfrac{5π}{3}\)

45)\(\dfrac{3π}{4}\)

Responda

\(\dfrac{π}{4}\), Quadrante II,\(\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}\),\(\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}\)

(46)\(\dfrac{4π}{3}\)

47)\(\dfrac{2π}{3}\)

Responda

\(\dfrac{π}{3}\), Quadrante II,\( \sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}\),\( \cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}\)

48)\(\dfrac{5π}{6}\)

49)\(\dfrac{7π}{4}\)

Resposta

\(\dfrac{π}{4}\), Quadrante IV,\( \sin \left(\dfrac{7π}{4}\right)=−\dfrac{\sqrt{2}}{2}\),\( \cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}\)

Para os exercícios 50-59, encontre o valor solicitado.

50) Se\(\cos (t)=\dfrac{1}{7}\) e\(t\) estiver no\(4^{th}\) quadrante, encontre\( \sin (t)\).

51) Se\( \cos (t)=\dfrac{2}{9}\) e\(t\) estiver no\(1^{st}\) quadrante, encontre\(\sin (t)\).

Responda

\(\dfrac{\sqrt{77}}{9}\)

52) Se\(\sin (t)=\dfrac{3}{8}\) e\(t\) estiver no\(2^{nd}\) quadrante, encontre\( \cos (t)\).

53) Se\( \sin (t)=−\dfrac{1}{4}\) e\(t\) estiver no\(3^{rd}\) quadrante, encontre\(\cos (t)\).

Responda

\(−\dfrac{\sqrt{15}}{4}\)

54) Encontre as coordenadas do ponto em um círculo com raio\(15\) correspondente a um ângulo de\(220°\).

55) Encontre as coordenadas do ponto em um círculo com raio\(20\) correspondente a um ângulo de\(120°\).

Responda

\((−10,10\sqrt{3})\)

56) Encontre as coordenadas do ponto em um círculo com raio\(8\) correspondente a um ângulo de\(\dfrac{7π}{4}\).

57) Encontre as coordenadas do ponto em um círculo com raio\(16\) correspondente a um ângulo de\(\dfrac{5π}{9}\).

Responda

\((–2.778,15.757)\)

58) Declare o domínio das funções seno e cosseno.

59) Declare a faixa das funções seno e cosseno.

Responda

\([–1,1]\)

Gráfica

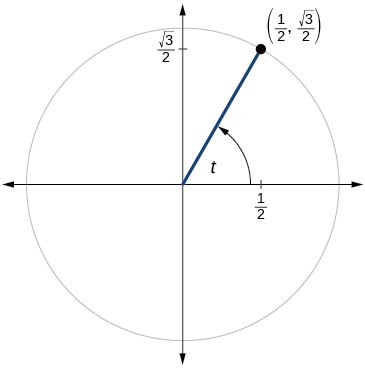
Para os exercícios 60-79, use o ponto dado no círculo unitário para encontrar o valor do seno e do cosseno de\(t\).

60)

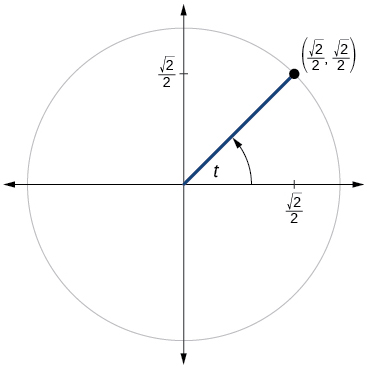
61)

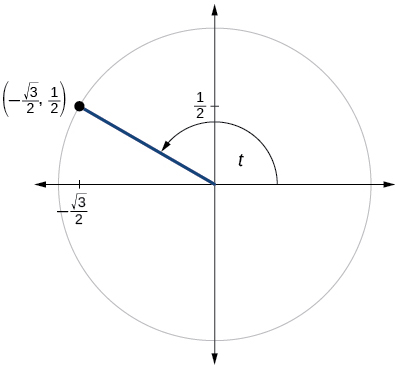
Responda

\( \sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}\)

62)

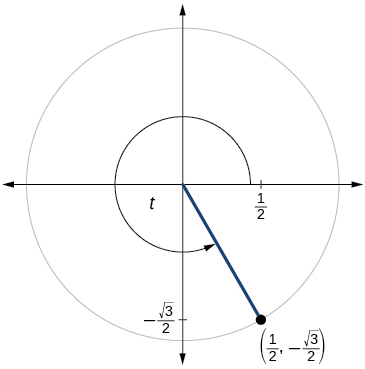
63)

Responda

\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}\)

64)

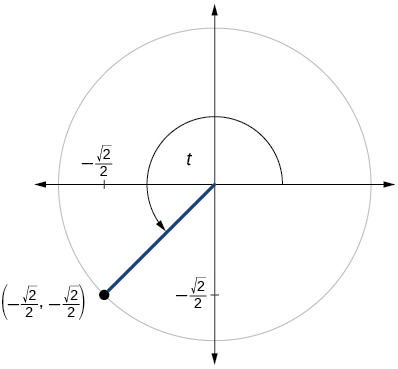
65)

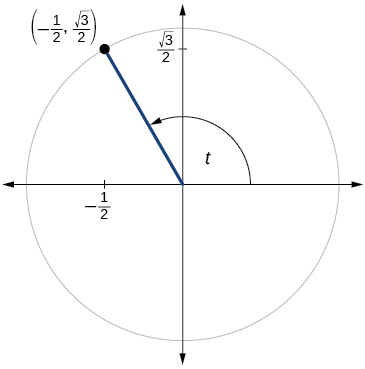
Responda

\( \sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}\)

66)

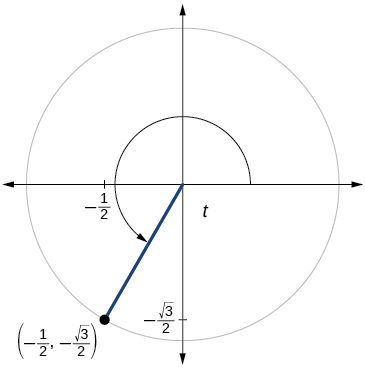
67)

Responda

\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}\)

68)

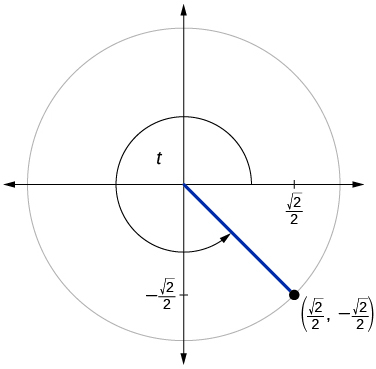
69)

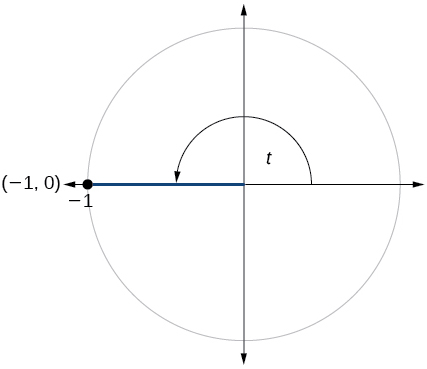
Responda

\( \sin t=0, \cos t=−1\)

70)

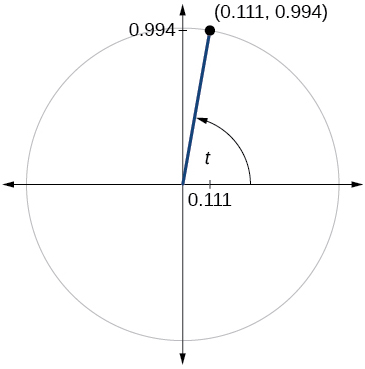
71)

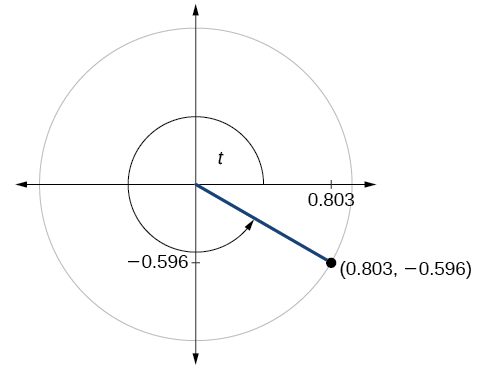
Responda

\( \sin t=−0.596, \cos t=0.803\)

72)

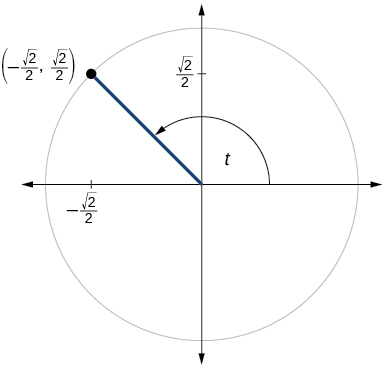
73)

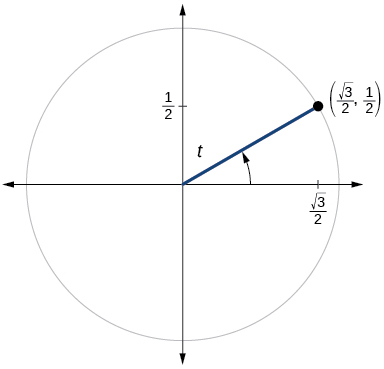
Responda

\(\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}\)

74)

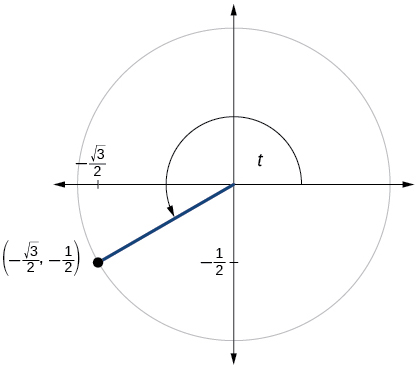
75)

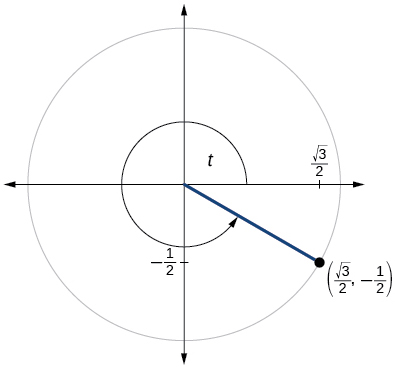
Responda

\( \sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2} \)

76)

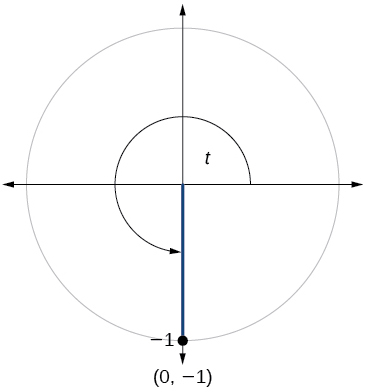
77)

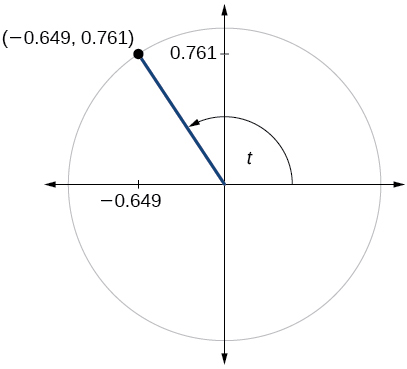
Responda

\( \sin t=0.761, \cos t=−0.649 \)

78)

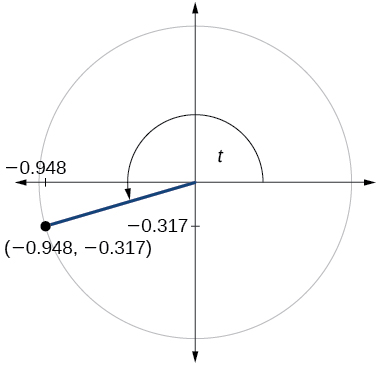
79)

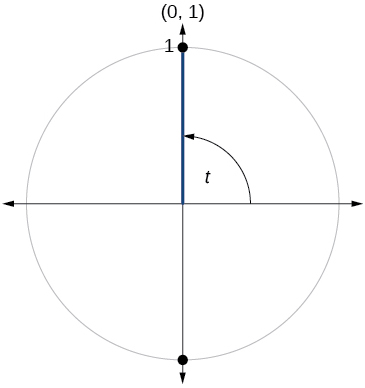
Responda

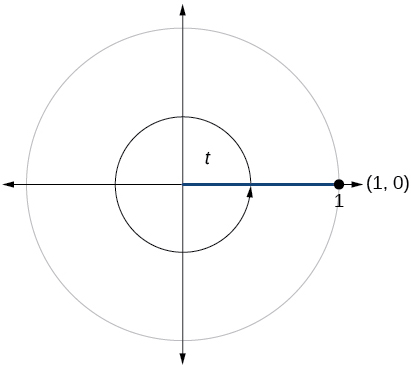
\( \sin t=1, \cos t=0\)

Tecnologia

Para os exercícios 80-89, use uma calculadora gráfica para avaliar.

80)\( \sin \dfrac{5π}{9}\)

81)\(cos \dfrac{5π}{9}\)

Responda

\(−0.1736\)

(82)\( \sin \dfrac{π}{10}\)

83)\( \cos \dfrac{π}{10}\)

Responda

\(0.9511\)

84)\( \sin \dfrac{3π}{4}\)

85)\(\cos \dfrac{3π}{4}\)

Responda

\(−0.7071\)

86)\( \sin 98° \)

87)\( \cos 98° \)

Responda

\(−0.1392\)

88)\( \cos 310° \)

89)\( \sin 310° \)

Responda

\(−0.7660\)

Extensões

Para os exercícios 90-99, avalie.

90)\( \sin \left(\dfrac{11π}{3}\right) \cos \left(\dfrac{−5π}{6}\right)\)

91)\( \sin \left(\dfrac{3π}{4}\right) \cos \left(\dfrac{5π}{3}\right) \)

Responda

\(\dfrac{\sqrt{2}}{4}\)

(92)\( \sin \left(− \dfrac{4π}{3}\right) \cos \left(\dfrac{π}{2}\right)\)

93)\( \sin \left(\dfrac{−9π}{4}\right) \cos \left(\dfrac{−π}{6}\right)\)

Responda

\(−\dfrac{\sqrt{6}}{4}\)

94)\( \sin \left(\dfrac{π}{6}\right) \cos \left(\dfrac{−π}{3}\right) \)

95)\( \sin \left(\dfrac{7π}{4}\right) \cos \left(\dfrac{−2π}{3}\right) \)

Responda

\(\dfrac{\sqrt{2}}{4}\)

96)\( \cos \left(\dfrac{5π}{6}\right) \cos \left(\dfrac{2π}{3}\right)\)

(97)\( \cos \left(\dfrac{−π}{3}\right) \cos \left(\dfrac{π}{4}\right) \)

Responda

\(\dfrac{\sqrt{2}}{4}\)

98)\( \sin \left(\dfrac{−5π}{4}\right) \sin \left(\dfrac{11π}{6}\right)\)

99)\( \sin (π) \sin \left(\dfrac{π}{6}\right) \)

Responda

\(0\)

Aplicativos do mundo real

Para os exercícios 100-104, use este cenário: uma criança entra em um carrossel que leva um minuto para girar uma vez. A criança entra no ponto\((0,1)\), ou seja, na posição norte devida. Suponha que o carrossel gire no sentido anti-horário.

100) Quais são as coordenadas da criança após\(45\) alguns segundos?

101) Quais são as coordenadas da criança após\(90\) alguns segundos?

Responda

\((0,–1)\)

102) Quais são as coordenadas da criança após\(125\) alguns segundos?

103) Quando a criança terá as coordenadas\((0.707,–0.707)\) se a viagem durar\(6\) minutos? (Há várias respostas.)

Responda

\(37.5\)segundos,\(97.5\) segundos,\(157.5\) segundos,\(217.5\) segundos,\(277.5\) segundos,\(337.5\) segundos

104) Quando a criança terá as coordenadas\((−0.866,−0.5)\) se a viagem durar\(6\) minutos?

5.3: As outras funções trigonométricas

Verbal

1) Em um intervalo de\([ 0,2π )\), os valores de seno e cosseno de uma medida em radianos podem ser iguais? Em caso afirmativo, onde?

Responda

Sim, quando o ângulo de referência é\(\dfrac{π}{4}\) e o lado terminal do ângulo está nos quadrantes I e III. Assim, em\(x=\dfrac{π}{4},\dfrac{5π}{4}\), os valores de seno e cosseno são iguais.

2) O que você estimaria o cosseno de\(\pi \) graus? Explique seu raciocínio.

3) Para qualquer ângulo no quadrante II, se você soubesse o seno do ângulo, como você poderia determinar o cosseno do ângulo?

Responda

Substitua o seno do ângulo por\(y\) no Teorema de Pitágoras\(x^2+y^2=1\). Resolva\(x\) e pegue a solução negativa.

4) Descreva a função secante.

5) A tangente e a cotangente têm um período de\(π\). O que isso nos diz sobre a saída dessas funções?

Responda

As saídas de tangente e cotangente se repetirão a cada\(π\) unidade.

Algébrico

Para os exercícios 6-17, encontre o valor exato de cada expressão.

6)\( \tan \dfrac{π}{6}\)

7)\(\sec \dfrac{π}{6}\)

Responda

\(\dfrac{2\sqrt{3}}{3}\)

8)\( \csc \dfrac{π}{6}\)

9)\( \cot \dfrac{π}{6}\)

Responda

\(\sqrt{3}\)

10)\( \tan \dfrac{π}{4}\)

11)\( \sec \dfrac{π}{4}\)

Responda

\(\sqrt{2}\)

12)\( \csc \dfrac{π}{4}\)

13)\( \cot \dfrac{π}{4}\)

Responda

\(1\)

14)\( \tan \dfrac{π}{3}\)

15)\( \sec \dfrac{π}{3}\)

Responda

\(2\)

16)\( \csc \dfrac{π}{3}\)

17)\( \cot \dfrac{π}{3}\)

Responda

\(\dfrac{\sqrt{3}}{3}\)

Para os exercícios 18-48, use ângulos de referência para avaliar a expressão.

18)\( \tan \dfrac{5π}{6}\)

19)\( \sec \dfrac{7π}{6}\)

Responda

\(−\dfrac{2\sqrt{3}}{3}\)

20)\( \csc \dfrac{11π}{6}\)

21)\( \cot \dfrac{13π}{6}\)

Responda

\(\sqrt{3}\)

22)\( \tan \dfrac{7π}{4}\)

23)\( \sec \dfrac{3π}{4}\)

Responda

\(−\sqrt{2}\)

24)\( \csc \dfrac{5π}{4}\)

25)\( \cot \dfrac{11π}{4}\)

Responda

\(−1\)

26)\( \tan \dfrac{8π}{3}\)

27)\( \sec \dfrac{4π}{3}\)

Responda

\(−2\)

28)\( \csc \dfrac{2π}{3}\)

29)\( \cot \dfrac{5π}{3}\)

Responda

\(−\dfrac{\sqrt{3}}{3}\)

30)\( \tan 225°\)

31)\( \sec 300°\)

Responda

\(2\)

32)\( \csc 150°\)

33)\( \cot 240°\)

Responda

\(\dfrac{\sqrt{3}}{3}\)

34)\( \tan 330°\)

(35)\( \sec 120°\)

Responda

\(−2\)

36)\( \csc 210°\)

37)\( \cot 315°\)

Responda

\(−1\)

38) Se\( \sin t= \dfrac{3}{4}\), e\(t\) estiver no quadrante II, encontre\( \cos t, \sec t, \csc t, \tan t, \cot t \).

39) Se\( \cos t=−\dfrac{1}{3},\) e\(t\) estiver no quadrante III, encontre\( \sin t, \sec t, \csc t, \tan t, \cot t\).

Responda

E se\(\sin t=−\dfrac{2\sqrt{2}}{3}, \sec t=−3, \csc t=−\csc t=−\dfrac{3\sqrt{2}}{4},\tan t=2\sqrt{2}, \cot t= \dfrac{\sqrt{2}}{4}\)

40) Se\(\tan t=\dfrac{12}{5},\) e\(0≤t< \dfrac{π}{2}\), encontre\( \sin t, \cos t, \sec t, \csc t,\)\(\cot t\) e.

41) Se\( \sin t= \dfrac{\sqrt{3}}{2}\)\( \sec t, \csc t, \tan t,\) e\( \cos t=\dfrac{1}{2},\) encontre\( \cot t\) e.

Responda

\( \sec t=2, \csc t=\csc t=\dfrac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}\)

42) Se\( \sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°\).

43) Se\( \sin t= \dfrac{\sqrt{2}}{2},\) o que é o\( \sin (−t)\)?

Responda

\(−\dfrac{\sqrt{2}}{2}\)

44) Se\( \cos t= \dfrac{1}{2},\) o que é o\( \cos (−t)\)?

45) Se\( \sec t=3.1,\) o que é o\( \sec (−t)\)?

Responda

\(3.1\)

46) Se\( \csc t=0.34,\) o que é o\( \csc (−t)\)?

47) Se\( \tan t=−1.4,\) o que é o\( \tan (−t)\)?

Responda

\(1.4\)

48) Se\( \cot t=9.23,\) o que é o\( \cot (−t)\)?

Gráfica

Para os exercícios 49-51, use o ângulo no círculo unitário para encontrar o valor de cada uma das seis funções trigonométricas.

49)

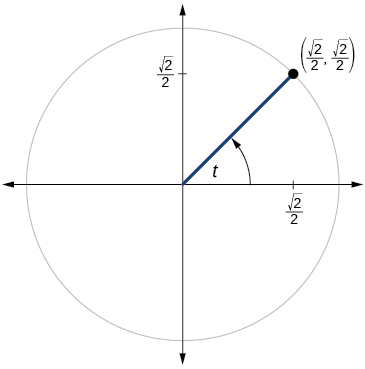
Responda

\( \sin t= \dfrac{\sqrt{2}}{2}, \cos t= \dfrac{\sqrt{2}}{2}, \tan t=1,\cot t=1,\sec t= \sqrt{2}, \csc t= \csc t= \sqrt{2} \)

50)

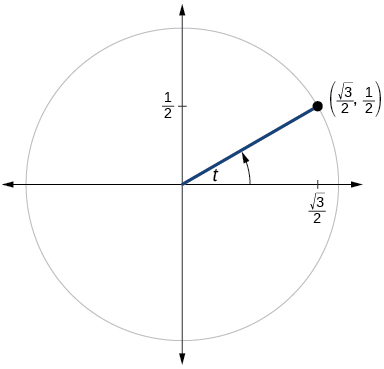
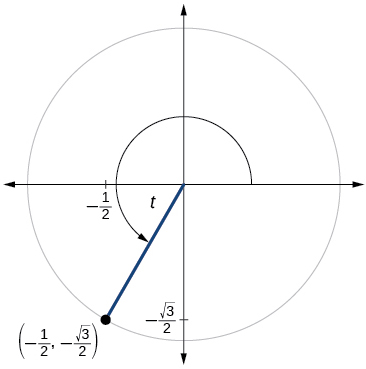
51)

Responda

\( \sin t=−\dfrac{\sqrt{3}}{2}, \cos t=−\dfrac{1}{2}, \tan t=\sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}, \sec t=−2, \csc t=−\csc t=−\dfrac{2\sqrt{3}}{3} \)

Tecnologia

Para os exercícios 52-61, use uma calculadora gráfica para avaliar.

52)\( \csc \dfrac{5π}{9}\)

53)\( \cot \dfrac{4π}{7}\)

Responda

\(–0.228\)

54)\( \sec \dfrac{π}{10}\)

55)\( \tan \dfrac{5π}{8}\)

Responda

\(–2.414\)

56)\( \sec \dfrac{3π}{4}\)

57)\( \csc \dfrac{π}{4}\)

Responda

\(1.414\)

(58)\( \tan 98°\)

(59)\( \cot 33°\)

Responda

\(1.540\)

60)\( \cot 140°\)

61)\( \sec 310° \)

Responda

\(1.556\)

Extensões

Para os exercícios 62-69, use identidades para avaliar a expressão.

62) Se\(\tan (t)≈2.7,\) e\( \sin (t)≈0.94,\) encontrar\( \cos (t)\).

63) Se\( \tan (t)≈1.3,\) e\( \cos (t)≈0.61\), encontre\( \sin (t)\).

Responda

\( \sin (t)≈0.79 \)

64) Se\( \csc (t)≈3.2,\)\( \csc (t)≈3.2,\) e\( \cos (t)≈0.95,\) encontrar\( \tan (t)\).

65) Se\( \cot (t)≈0.58,\) e\( \cos (t)≈0.5,\) encontrar\( \csc (t)\).

Responda

\( \csc (t)≈1.16\)

66) Determine se a função\(f(x)=2 \sin x \cos x\) é par, ímpar ou nenhuma.

67) Determine se a função\(f(x)=3 \sin ^2 x \cos x + \sec x\) é par, ímpar ou nenhuma.

Responda

uniforme

68) Determine se a função\(f(x)= \sin x −2 \cos ^2 x \) é par, ímpar ou nenhuma.

69) Determine se a função\(f(x)= \csc ^2 x+ \sec x\) é par, ímpar ou nenhuma.

Responda

uniforme

Para os exercícios 70-71, use identidades para simplificar a expressão.

70)\( \csc t \tan t\)

71)\( \dfrac{\sec t}{ \csc t}\)

Responda

\( \dfrac{ \sin t}{ \cos t}= \tan t\)

Aplicativos do mundo real

72) A quantidade de luz solar em uma determinada cidade pode ser modelada pela função\(h=15 \cos \left(\dfrac{1}{600}d\right),\) onde\(h\) representa as horas de luz solar e\(d\) é o dia do ano. Use a equação para descobrir quantas horas de luz solar existem em 10 de fevereiro, o\(42^{nd}\) dia do ano. Indique o período da função.

73) A quantidade de luz solar em uma determinada cidade pode ser modelada pela função\(h=16 \cos \left(\dfrac{1}{500}d\right)\), onde\(h\) representa as horas de luz solar e\(d\) é o dia do ano. Use a equação para descobrir quantas horas de luz solar existem em 24 de setembro, o\(267^{th}\) dia do ano. Indique o período da função.

Responda

\(13.77\)horas, período:\(1000π\)

74) A equação\(P=20 \sin (2πt)+100\) modela a pressão arterial,\(P\), onde\(t\) representa o tempo em segundos.

1. Encontre a pressão arterial após\(15\) alguns segundos.
2. Quais são as pressões arterial máxima e mínima?

75) A altura de um pistão\(h\), em polegadas, pode ser modelada pela equação em\(y=2 \cos x+6,\) que\(x\) representa o ângulo da manivela. Encontre a altura do pistão quando o ângulo da manivela estiver\(55°\).

Responda

\(7.73\)polegadas

76) A altura de um pistão\(h\), em polegadas, pode ser modelada pela equação em\(y=2 \cos x+5,\) que\(x\) representa o ângulo da manivela. Encontre a altura do pistão quando o ângulo da manivela estiver\(55°\).

5.4: Trigonometria do triângulo reto

Verbal

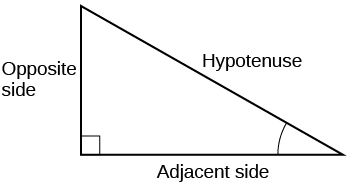
1) Para o triângulo direito fornecido, identifique o lado adjacente, o lado oposto e a hipotenusa para o ângulo indicado.

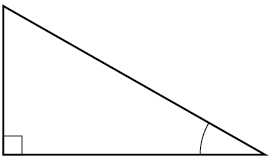
Responda

2) Quando um triângulo reto com uma hipotenusa de\(1\) é colocado no círculo unitário, quais lados do triângulo correspondem às\(y\) coordenadas\(x\) - e -?

3) A tangente de um ângulo compara quais lados do triângulo reto?

Resposta

A tangente de um ângulo é a razão entre o lado oposto e o lado adjacente.

4) Qual é a relação entre os dois ângulos agudos em um triângulo reto?

5) Explique a identidade da cofunção.

Resposta

Por exemplo, o seno de um ângulo é igual ao cosseno de seu complemento; o cosseno de um ângulo é igual ao seno de seu complemento.

Algébrico

Para os exercícios 6-9, use cofunções de ângulos complementares.

6)\( \cos (34°)= \sin (\_\_°)\)

7)\( \cos (\dfrac{π}{3})= \sin (\_\_\_) \)

Resposta

\(\dfrac{π}{6}\)

8)\( \csc (21°) = \sec (\_\_\_°)\)

9)\( \tan (\dfrac{π}{4})= \cot (\_\_)\)

Resposta

\(\dfrac{π}{4}\)

Para os exercícios 10-16, determine o comprimento dos lados faltantes se o lado\(a\) for o ângulo oposto\(A\), o lado\(b\) for o ângulo\(B\) oposto e o lado\(c\) for a hipotenusa.

10)\( \cos B= \dfrac{4}{5},a=10\)

11)\( \sin B= \dfrac{1}{2}, a=20\)

Resposta

\(b= \dfrac{20\sqrt{3}}{3},c= \dfrac{40\sqrt{3}}{3}\)

12)\( \tan A= \dfrac{5}{12},b=6\)

13)\( \tan A=100,b=100\)

Resposta

\(a=10,000,c=10,000.5\)

14)\(\sin B=\dfrac{1}{\sqrt{3}}, a=2 \)

15)\(a=5, ∡ A=60^∘\)

Resposta

\(b=\dfrac{5\sqrt{3}}{3},c=\dfrac{10\sqrt{3}}{3}\)

16)\(c=12, ∡ A=45^∘\)

Gráfica

Para os exercícios 17-22, use a Figura abaixo para avaliar cada função trigonométrica do ângulo\(A\).

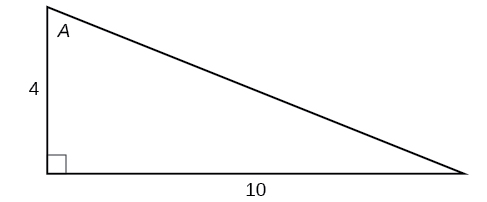
17)\(\sin A\)

Resposta

\(\dfrac{5\sqrt{29}}{29}\)

18)\( \cos A \)

19)\( \tan A \)

Resposta

\(\dfrac{5}{2}\)

20)\(\csc A \)

21)\( \sec A \)

Resposta

\(\dfrac{\sqrt{29}}{2}\)

22)\( \cot A \)

Para os exercícios 23-,28 use a Figura abaixo para avaliar cada função trigonométrica do ângulo\(A\).

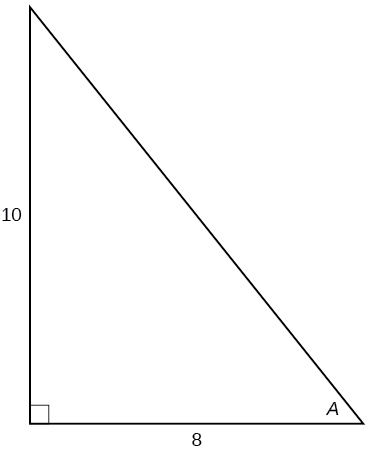
23)\( \sin A\)

Resposta

\(\dfrac{5\sqrt{41}}{41}\)

24)\( \cos A\)

25)\( \tan A \)

Resposta

\(\dfrac{5}{4}\)

26)\( \csc A\)

27)\( \sec A\)

Resposta

\(\dfrac{\sqrt{41}}{4}\)

28)\(\cot A\)

Para os exercícios 29-31, resolva os lados desconhecidos de um determinado triângulo.

29)

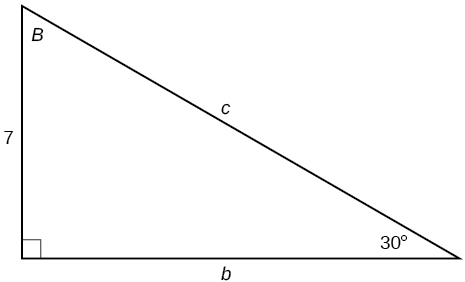
Resposta

\(c=14, b=7\sqrt{3}\)

30)

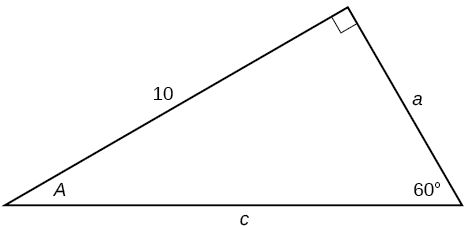
31)

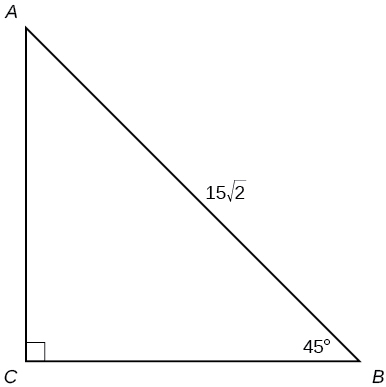
Resposta

\(a=15, b=15 \)

Tecnologia

Para os exercícios 32-41, use uma calculadora para encontrar o comprimento de cada lado com quatro casas decimais.

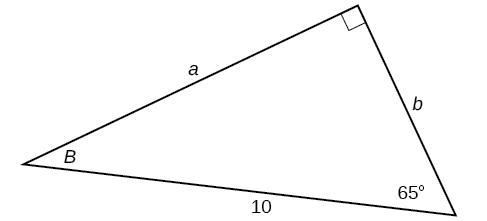
32)

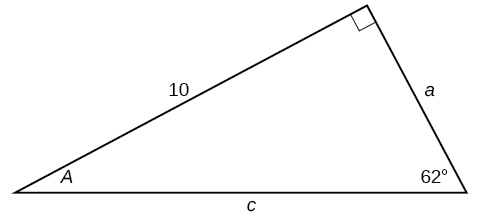
33)

Resposta

\(b=9.9970, c=12.2041\)

34)

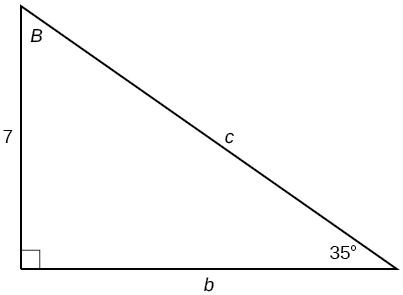
35)

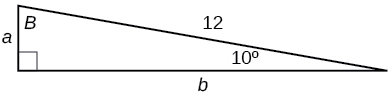
Resposta

\(a=2.0838, b=11.8177\)

36)

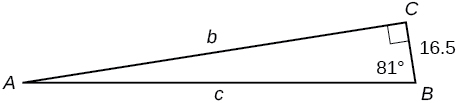
37)\(b=15, ∡B=15^∘\)

Resposta

\(a=55.9808,c=57.9555\)

38)\(c=200, ∡B=5^∘\)

39)\(c=50, ∡B=21^∘\)

Resposta

\(a=46.6790,b=17.9184\)

40)\(a=30, ∡A=27^∘\)

41)\(b=3.5, ∡A=78^∘\)

Resposta

\(a=16.4662,c=16.8341\)

Extensões

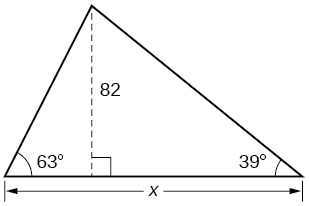
42) Encontrar\(x\).

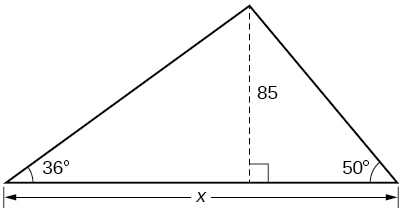
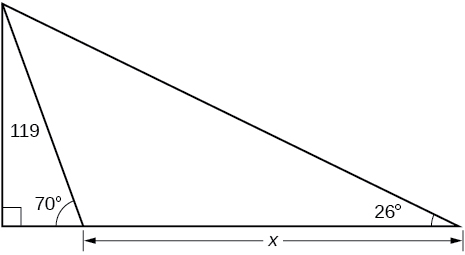
43) Encontrar\(x\).

Resposta

\(188.3159\)

44) Encontre\(x\).

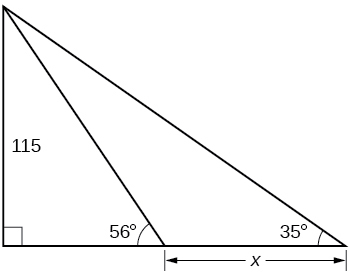
45) Encontrar\(x\).

Resposta

\(200.6737\)

46) Uma torre de rádio está localizada a\(400\) poucos metros de um prédio. De uma janela do prédio, uma pessoa determina que o ângulo de elevação até o topo da torre é\(36°\) e que o ângulo de depressão em relação à parte inferior da torre é\(23°\). Qual é a altura da torre?

47) Uma torre de rádio está localizada a\(325\) poucos metros de um prédio. De uma janela do prédio, uma pessoa determina que o ângulo de elevação até o topo da torre é\(43°\) e que o ângulo de depressão em relação à parte inferior da torre é\(31°\). Qual é a altura da torre?

Resposta

\(498.3471\)pés

48) Um monumento\(200\) de um metro de altura está localizado à distância. De uma janela de um prédio, uma pessoa determina que o ângulo de elevação até o topo do monumento é\(15°\) e que o ângulo de depressão em relação ao fundo da torre é\(2°\). A que distância a pessoa está do monumento?

49) Um monumento\(400\) de um metro de altura está localizado à distância. De uma janela de um prédio, uma pessoa determina que o ângulo de elevação até o topo do monumento é\(18°\) e que o ângulo de depressão em relação à parte inferior do monumento é\(3°\). A que distância a pessoa está do monumento?

Resposta

\(1060.09\)pés

50) Há uma antena no topo de um prédio. De um local a\(300\) pés da base do edifício, o ângulo de elevação até o topo do edifício é medido como sendo\(40°\). Do mesmo local, o ângulo de elevação até o topo da antena é medido como sendo\(43°\). Encontre a altura da antena.

51) Há um pára-raios no topo de um prédio. De um local a\(500\) pés da base do edifício, o ângulo de elevação até o topo do edifício é medido como sendo\(36°\). Do mesmo local, o ângulo de elevação até o topo do pára-raios é medido como sendo\(38°\). Encontre a altura do pára-raios.

Resposta

\(27.372\)pés

Aplicativos do mundo real

52) Uma escada\(33\) de pés se inclina contra um prédio de forma que o ângulo entre o solo e a escada seja\(80°\). Qual a altura da escada até a lateral do prédio?

53) Uma escada\(23\) de pés se inclina contra um prédio de forma que o ângulo entre o solo e a escada seja\(80°\). Qual a altura da escada até a lateral do prédio?

Resposta

\(22.6506\)pés

54) O ângulo de elevação até o topo de um edifício em Nova York é encontrado em\(9\) graus do solo a uma distância de um\(1\) quilômetro da base do edifício. Usando essas informações, encontre a altura do prédio.

55) O ângulo de elevação até o topo de um edifício em Seattle é encontrado em\(2\) graus do solo a uma distância de\(2\) quilômetros da base do edifício. Usando essas informações, encontre a altura do prédio.

Resposta

\(368.7633\)pés

56) Supondo que uma sequóia gigante de um\(370\) metro de altura cresça verticalmente, se eu andar uma certa distância da árvore e medir o ângulo de elevação até o topo da árvore\(60°\), a que distância estou da base da árvore?