6.R: Funções periódicas (revisão)

Last updated
Save as PDF

Page ID: 189176

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

6.1: Gráficos das funções seno e cosseno

Para os exercícios 1-8, represente graficamente as funções por dois períodos e determine a amplitude ou o fator de alongamento, o período, a equação da linha média e as assíntotas.

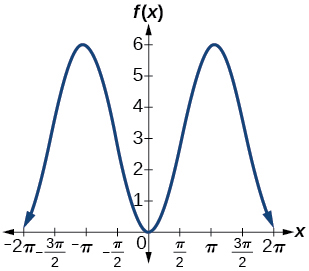
1)$f(x)=-3\cos x+3$

Responda

amplitude:$3$; período:$2\pi $; linha média:$y=3$; sem assíntotas

$6R6.1.1.png$

2)$f(x)=\dfrac{1}{4}\sin x$

3)$f(x)=3\cos\left ( x+\dfrac{\pi }{6} \right )$

Responda

amplitude:$3$; período:$2\pi $; linha média:$y=0$; sem assíntotas

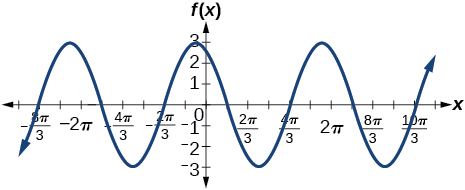
$6R6.1.3.png$

4)$f(x)=-2\sin\left ( x-\dfrac{2\pi }{3} \right )$

5)$f(x)=3\sin\left ( x-\dfrac{\pi }{4} \right )-4$

Responda

amplitude:$3$; período:$2\pi $; linha média:$y=-4$; sem assíntotas

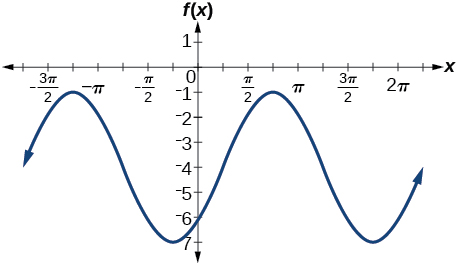
$6R6.1.5.png$

6)$f(x)=2\left (\cos\left ( x-\dfrac{4\pi }{3} \right )+1 \right )$

7)$f(x)=6\sin\left ( 3x-\dfrac{\pi }{6} \right )-1$

Responda

amplitude:$6$; período:$dfrac{2\pi }{3}$; linha média:$y=-1$; sem assíntotas

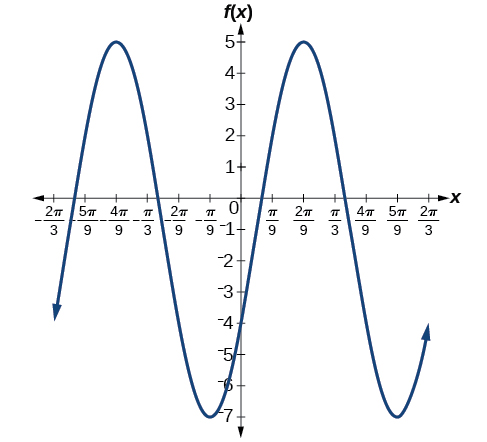
$6R6.1.7.png$

8)$f(x)=-100\sin(50x-20)$

6.2: Gráficos das outras funções trigonométricas

Para os exercícios 1-4, represente graficamente as funções por dois períodos e determine a amplitude ou o fator de alongamento, o período, a equação da linha média e as assíntotas.

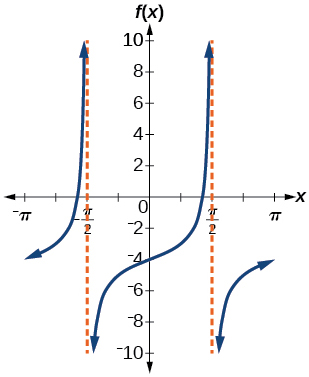
1)$f(x)=\tan x-4$

Responda

fator de alongamento: nenhum; ponto final:$\pi $; linha média:$y=-4$; assíntotas:$x=\dfrac{\pi }{2}+\pi k$, onde$k$ é um número inteiro

$6R6.2.1.png$

2)$f(x)=2\tan \left ( x-\dfrac{\pi }{6} \right )$

3)$f(x)=-3\tan (4x)-2$

Responda

fator de alongamento:$3$; período:$\dfrac{\pi }{4}$; linha média:$y=-2$; assíntotas:$x=\dfrac{\pi }{8}+\dfrac{\pi }{4}k$, onde$k$ é um número inteiro

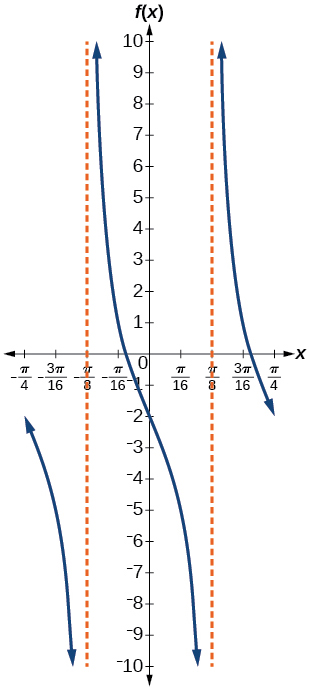
$6R6.2.3.png$

4)$f(x)=0.2\cos(0.1x)+0.3$

Para os exercícios de 5 a 10, faça um gráfico de dois períodos completos. Identifique o período, a mudança de fase, a amplitude e as assíntotas.

5)$f(x)=\dfrac{1}{3}\sec x$

Responda

amplitude: nenhuma; período:$2\pi $; sem mudança de fase; assíntotas:$x=\dfrac{\pi }{2}k$, onde$k$ é um número inteiro

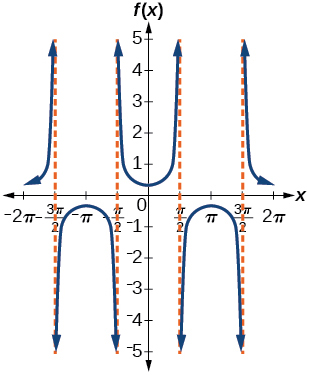
$6R6.2.5.png$

6)$f(x)=3\cot x$

7)$f(x)=4\csc (5x)$

Responda

amplitude: nenhuma; período:$\dfrac{2\pi }{5}$; sem mudança de fase; assíntotas:$x=\dfrac{\pi }{5}k$, onde$k$ é um número inteiro

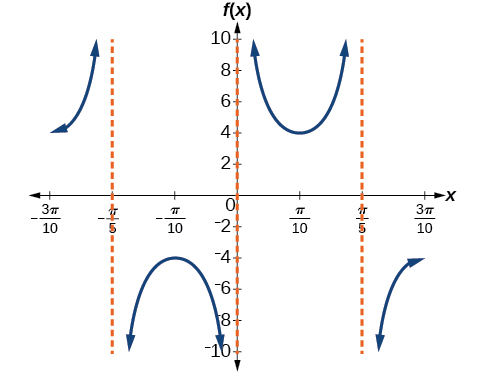
$6R6.2.7.png$

8)$f(x)=8\sec \left (\dfrac{1}{4}x \right )$

9)$f(x)=\dfrac{2}{3}\csc \left (\dfrac{1}{2}x \right )$

Responda

amplitude: nenhuma; período:$4\pi $; sem mudança de fase; assíntotas:$x=2\pi k$, onde$k$ é um número inteiro

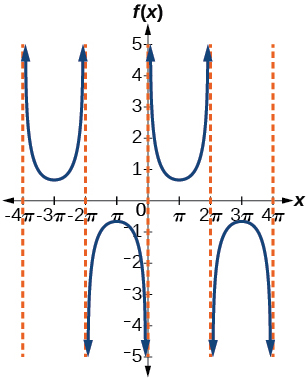
$6R6.2.9.png$

10)$f(x)=-\csc (2x+\pi)$

Para os exercícios 11-15, use este cenário: A população de uma cidade aumentou e diminuiu em um intervalo$20$ de um ano. Sua população pode ser modelada pela seguinte função:$y=12,000+8,000\sin(0.628x)$, onde o domínio são os anos desde 1980 e o alcance é a população da cidade.

11) Qual é a maior e menor população que a cidade pode ter?

Responda: maior:$20,000$; menor:$4,000$

12) Representar graficamente a função no domínio de$[0,40]$.

13) Quais são a amplitude, o período e a mudança de fase da função?

Responda: amplitude:$8,000$; período:$10$; mudança de fase:$0$

14) Sobre esse domínio, quando a população chega$18,000$? $13,000$?

15) Qual é a população prevista em 2007? 2010?

Responda: Em 2007, a população prevista é$4,413$. Em 2010, a população será$11,924$.

Para os exercícios 16a-16d, suponha que um peso esteja preso a uma mola e oscile para cima e para baixo, exibindo simetria.

16) Suponha que o gráfico da função de deslocamento seja mostrado na Figura abaixo, onde os valores no$x$ eixo -representam o tempo em segundos e o$y$ eixo -representa o deslocamento em polegadas.

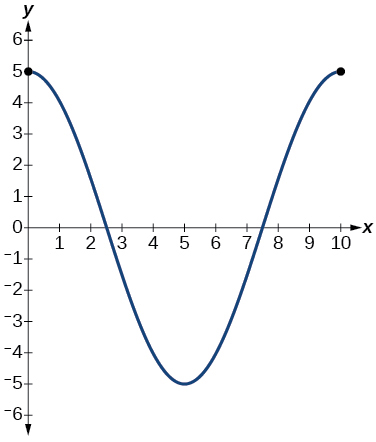
$6R6.2.16.png$

Dê a equação que modela o deslocamento vertical do peso na mola.
Em$\text{time} = 0$, qual é o deslocamento do peso?

Responda: $5$em.

Em que momento o deslocamento do ponto de equilíbrio é igual a zero?
Qual é o tempo necessário para que o peso retorne à sua altura inicial de$5$ polegadas? Em outras palavras, qual é o período da função de deslocamento?

Responda: $10$segundos

6.3: Funções trigonométricas inversas

Para os exercícios 1-11, encontre o valor exato sem o auxílio de uma calculadora.

1)$\sin ^{-1}(1)$

2)$\cos ^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )$

Responda: $\dfrac{\pi }{6}$

3)$\tan ^{-1}(-1)$

4)$\cos ^{-1}\left ( \dfrac{1}{\sqrt{2}} \right )$

Responda: $\dfrac{\pi }{4}$

5)$\sin ^{-1}\left ( \dfrac{-\sqrt{3}}{2} \right )$

6)$\sin ^{-1}\left (\cos \left (\dfrac{\pi }{6} \right ) \right )$

Responda: $\dfrac{\pi }{3}$

7)$\cos ^{-1}\left (\tan \left (\dfrac{3\pi }{4} \right ) \right )$

8)$\sin \left (\sec^{-1} \left (\dfrac{3}{5} \right ) \right )$

Responda: Sem solução

9)$\cot \left (\sin^{-1} \left (\dfrac{3}{5} \right ) \right )$

10)$\tan \left (\cos^{-1} \left (\dfrac{5}{13} \right ) \right )$

Responda: $\dfrac{12}{5}$

11)$\sin \left (\cos^{-1} \left (\dfrac{x}{x+1} \right ) \right )$

12) Faça um gráfico$f(x)=\cos x$ e$f(x)=\sec x$ descreva o intervalo$[0,2\pi )$ e explique quaisquer observações.

Responda

Os gráficos não são simétricos em relação à linha$y=x$. Eles são simétricos em relação ao$y$ eixo y.

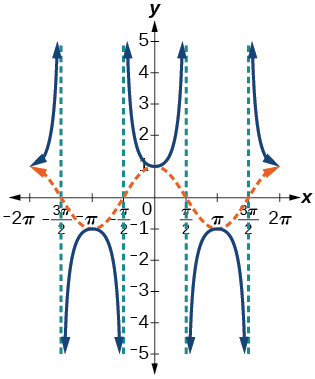
$6R6.3.12.png$

13) Representar graficamente$f(x)=\sin x$$f(x)=\csc x$ e explicar quaisquer observações.

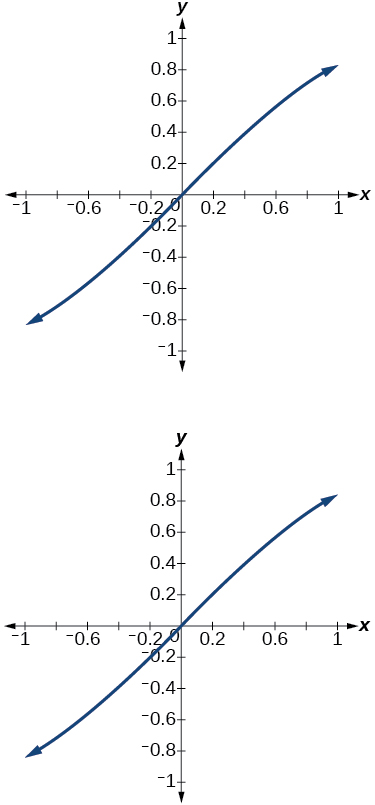
14) Representar graficamente a função$f(x)=\dfrac{x}{1}-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}$ no intervalo$[-1,1]$ e comparar o gráfico com o gráfico de$f(x)=\sin x$ no mesmo intervalo. Descreva todas as observações.

Responda

Os gráficos parecem ser idênticos.

$6R6.3.14.png$

Teste prático

Para os exercícios 1-13, esboce o gráfico de cada função por dois períodos completos. Determine a amplitude, o período e a equação da linha média.

1)$f(x)=0.5\sin x$

Responda

amplitude:$0.5$; período:$2\pi $; linha média$y=0$

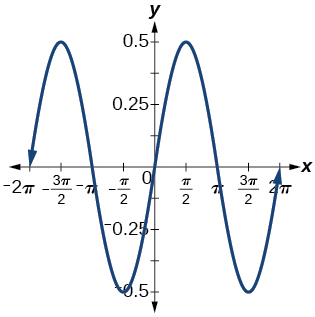
$6RP 1.png$ $  y = 0   " role="presentation" style="background-color:transparent;border-bottom-color:rgb(85, 85, 85);border-bottom-style:none;border-bottom-width:0px;border-image-outset:0;border-image-repeat:stretch;border-image-slice:100%;border-image-source:none;border-image-width:1;border-left-color:rgb(85, 85, 85);border-left-style:none;border-left-width:0px;border-right-color:rgb(85, 85, 85);border-right-style:none;border-right-width:0px;border-top-color:rgb(85, 85, 85);border-top-style:none;border-top-width:0px;box-sizing:border-box;direction:ltr;display:inline;float:none;font-family:Helvetica Neue,Helvetica,Arial,sans-serif;font-size-adjust:none;font-style:normal;font-variant:normal;font-weight:400;letter-spacing:normal;line-height:normal;margin-bottom:0px;margin-left:0px;margin-right:0px;margin-top:0px;max-height:none;max-width:none;min-height:0px;min-width:0px;orphans:2;padding-bottom:0px;padding-left:0px;padding-right:0px;padding-top:0px;position:relative;text-align:left;text-decoration:none;text-indent:0px;text-transform:none;-webkit-text-stroke-width:0px;white-space:nowrap;word-spacing:0px;word-wrap:normal;" tabindex="0">$ y = 0 y=0 y=0

2)$f(x)=5\cos x$

3)$f(x)=5\sin x$

Responda

amplitude:$0.5$; período:$2\pi $; linha média$y=0$

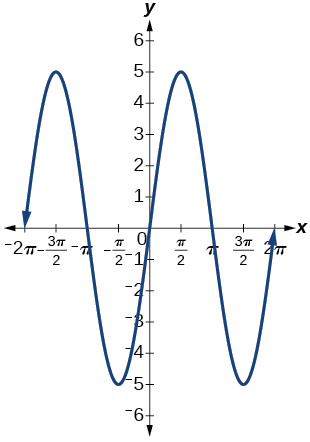
$6RP 3.png$

4)$f(x)=\sin (3x)$

5)$f(x)=-\cos \left ( x+\dfrac{\pi }{3} \right )+1$

Responda

amplitude:$1$; período:$2\pi $; linha média$y=1$

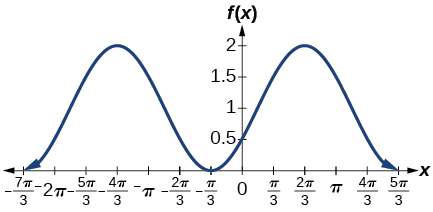
$6RP 5.png$

6)$f(x)=5\sin \left (3\left ( x-\dfrac{\pi }{6} \right ) \right )+4$

7)$f(x)=3\cos \left ( \dfrac{1}{3}x-\dfrac{5\pi }{6} \right )$

Responda

amplitude:$3$; período:$6\pi $; linha média$y=0$

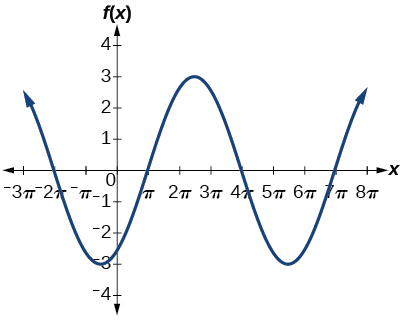
$6RP 7.png$

8)$f(x)=\tan (4x)$

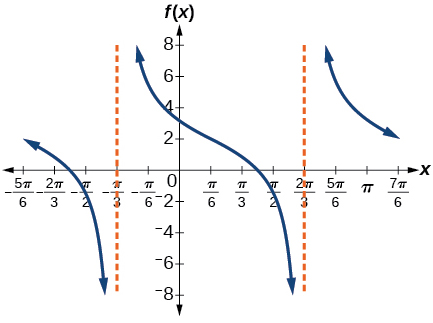
9)$f(x)=-2\tan \left ( x-\dfrac{7\pi }{6} \right )+2$

Responda

amplitude: nenhuma; período:$\pi $; linha média$y=0$, assíntotas:$x=\dfrac{2\pi }{3}+\pi k$,onde$k$ é um número inteiro

$6RP 9.png$

10)$f(x)=\pi \cos(3x+\pi)$

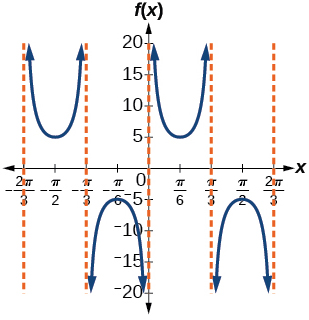
11)$f(x)=5\csc(3x)$

Responda

amplitude: nenhuma; período:$\dfrac{2\pi }{3}$; linha média$y=0$, assíntotas:$x=\dfrac{\pi }{3}k$,onde$k$ é um número inteiro

$6RP 11.png$

12)$f(x)=\pi \sec \left ( \dfrac{\pi }{2}x \right )$

13)$f(x)=2\csc \left ( x+\dfrac{\pi }{4} \right )-3$

Resposta

amplitude: nenhuma; período:$2\pi $; linha média$y=-3$

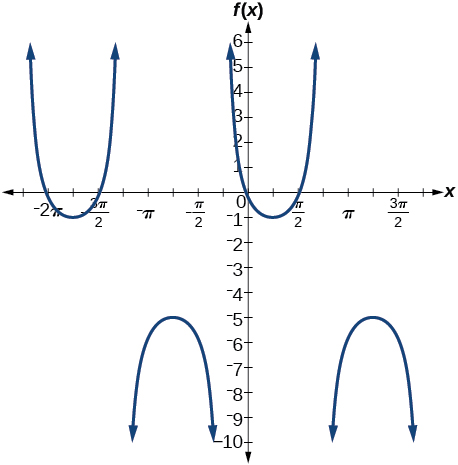
$6RP 13.png$

Para os exercícios 14-16, determine a amplitude, o período e a linha média do gráfico e, em seguida, encontre uma fórmula para a função.

14) Dê em termos de uma função senoidal.

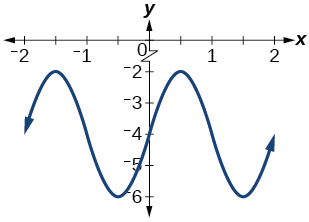
$6RP 14.png$

15) Dê em termos de uma função senoidal.

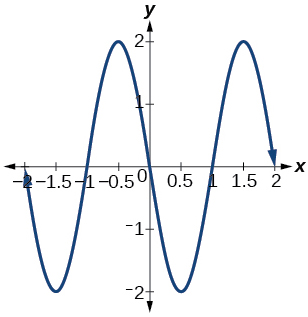
$6RP 15.png$

Resposta: amplitude:$2$; período:$2$; linha média:$y=0$;$f(x)=2\sin(\pi (x-1))$

16) Dê em termos de uma função tangente.

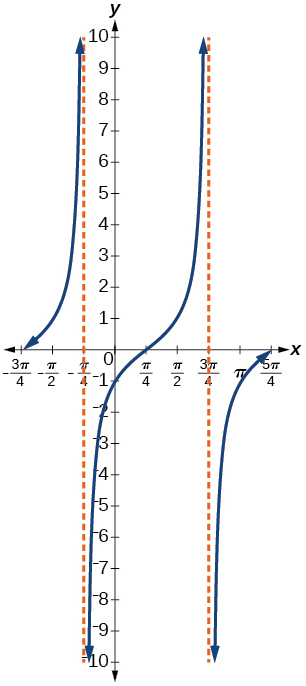
$6RP 16.png$

Para os exercícios 17-20, determine a amplitude, o período, a mudança de fase e a linha média.

17)$y=\sin\left(\dfrac{\pi}{6}x+\pi \right)-3$

Resposta: amplitude:$1$; período:$12$; mudança de fase:$-6$; linha média:$y=-3$

18)$y=8\sin\left(\dfrac{7\pi}{6}x+\dfrac{7\pi}{2} \right)+6$

19) A temperatura externa ao longo de um dia pode ser modelada como uma função senoidal. Suponha que você saiba que a temperatura é$68^{\circ}$ F à meia-noite e as temperaturas altas e baixas durante o dia são$80^{\circ}$ F e$56^{\circ}$ F, respectivamente. Supondo que$t$ seja o número de horas desde a meia-noite, encontre uma função para a temperatura$D$,, em termos de$t$.

Resposta: $D(t)=68-12\sin\left(\dfrac{\pi}{12}x \right)$

20) A água é bombeada para uma caixa de armazenamento e esvaziada de acordo com uma taxa periódica. A profundidade da água é de$3$ pés no nível mais baixo às 2:00 da manhã e$71$ pés no ponto mais alto, o que ocorre a cada$5$ hora. Escreva uma função de cosseno que modela a profundidade da água em função do tempo e, em seguida, represente graficamente a função por um período.

Para os exercícios 21-25, encontre o período e o deslocamento horizontal de cada função.

21)$g(x)=3\tan(6x+42)$

Resposta: período:$\dfrac{\pi}{6}$; deslocamento horizontal:$-7$

22)$n(x)=4\csc \left(\dfrac{5\pi }{3}x-\dfrac{20\pi }{3} \right)$

23) Escreva a equação para o gráfico na Figura abaixo em termos da função secante e forneça o período e a mudança de fase.

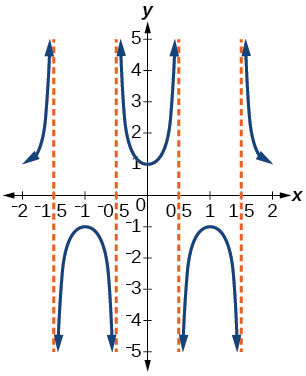
$6RP 23.png$

Resposta: $f(x)=\sec(\pi x)$; período:$2$; mudança de fase:$0$

24) Se$\tan x=3$, achar$\tan (-x)$.

25) Se$\sec x=4$, encontre$\sec (-x)$.

Resposta: $4$

Para os exercícios 26-28, faça um gráfico das funções na janela especificada e responda às perguntas.

26) Gráfico$m(x)=\sin(2x)+\cos(3x)$ na janela de visualização$[-10,10]$ por$[-3,3]$. Aproxime o período do gráfico.

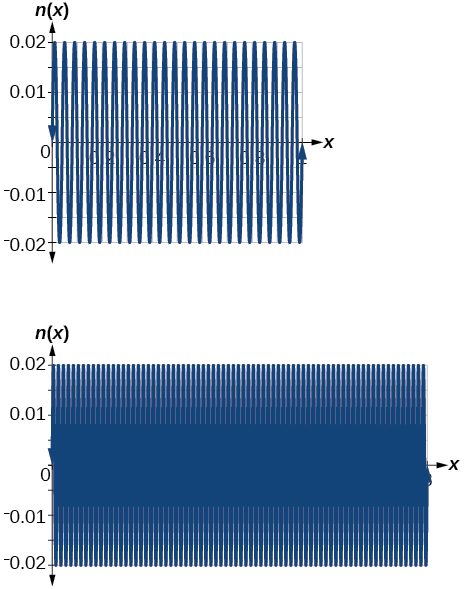
27) Gráfico$n(x)=0.02\sin(50\pi x)$ dos seguintes domínios em$x:[0,1]$ e$[0,3]$. Suponha que essa função modela ondas sonoras. Por que essas visões seriam tão diferentes?

Resposta

As vistas são diferentes porque o período da onda é$125$. Em um domínio maior, haverá mais ciclos do gráfico.

$6RP 27.png$

28) Faça um$f(x)=\dfrac{\sin x}{x}$ gráfico$[-0.5,0.5]$ e explique quaisquer observações.

Para os exercícios 29-31, deixe$f(x)=\dfrac{3}{5}\cos(6x)$.

29) Qual é o maior valor possível$f(x)$?

Resposta: $\dfrac{3}{5}$

30) Qual é o menor valor possível$f(x)$?

31) Onde a função está aumentando no intervalo$[0,2\pi ]$?

Resposta: Nos intervalos aproximados$(0.5,1),(1.6,2.1),(2.6,3.1),(3.7,4.2),(4.7,5.2),(5.6,6.28)$

Para os exercícios 32-33, encontre e represente graficamente um período da função periódica com a amplitude, o período e a mudança de fase fornecidos.

32) Curva senoidal com amplitude$3$, período$\dfrac{\pi }{3}$, e mudança de fase$(h,k)=\left(\dfrac{\pi }{4},2\right)$

33) Curva de cosseno com amplitude$2$, período$\dfrac{\pi }{6}$, e mudança de fase$(h,k)=\left(-\dfrac{\pi }{4},3\right)$

Resposta

$f(x)=2\cos\left ( 12\left ( x+\dfrac{\pi }{4} \right ) \right )+3$

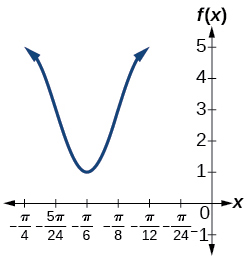
$6RP 33.png$

Para os exercícios 34-35, represente graficamente a função. Descreva o gráfico e, sempre que aplicável, qualquer comportamento periódico, amplitude, assíntotas ou pontos indefinidos.

34)$f(x)=5\cos(3x)+4\sin(2x)$

(35)$f(x)=e^{(sint)}$

Resposta

Este gráfico é periódico com um período de$2\pi $

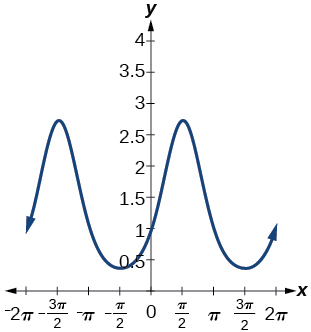
$6RP 35.png$

Para os exercícios 36-43, encontre o valor exato.

36)$\sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )$

37)$\tan^{-1}\left ( \sqrt{3} \right )$

Resposta: $\dfrac{\pi }{3}$

38)$\cos^{-1}\left ( -\dfrac{\sqrt{3}}{2} \right )$

39)$\cos^{-1}\left ( \sin(\pi) \right )$

Resposta: $\dfrac{\pi }{2}$

40)$\cos^{-1}\left ( \tan \left (\dfrac{7\pi}{4} \right ) \right )$

41)$\cos(\sin^{-1}(1-2x))$

Resposta: $\sqrt{1-(1-2x)^2}$

(42)$\cos^{-1}(-0.4)$

43)$\cos \left (\tan^{-1}\left(x^2\right) \right )$

Resposta: $\dfrac{1}{\sqrt{1+x^4}}$

Para os exercícios 44-46, suponha$\sin t=\dfrac{x}{x+1}$. Avalie as seguintes expressões.

44)$\tan t$

45)$csc t$

Resposta: $\dfrac{x+1}{x}$

46) Dada a Figura, determine a medida do ângulo$\theta $ com três casas decimais. Resposta em radianos.

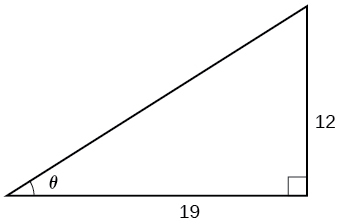
$6RP 46.png$

Para os exercícios 47-49, determine se a equação é verdadeira ou falsa.

47)$\arcsin\left(\sin\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}$

Resposta: Falso

48)$\arccos\left(\cos\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}$

49) O nível de uma estrada é$7\%$. Isso significa que para cada distância horizontal de$100$ pés na estrada, a elevação vertical é de$7$ pés. Encontre o ângulo que a estrada faz com a horizontal em radianos.

Resposta: aproximadamente$0.07$ radianos