5.4: Trigonometria do triângulo reto
- Page ID
- 189311
Objetivos de
- Use triângulos retos para avaliar funções trigonométricas.
- Encontre valores de função para 30° (\(\dfrac{\pi}{6}\)), 45° (\(\dfrac{\pi}{4}\)) e 60° (\(\dfrac{\pi}{3}\)).
- Use cofunções iguais de ângulos complementares.
- Use as definições de funções trigonométricas de qualquer ângulo.
- Use a trigonometria do triângulo reto para resolver os problemas aplicados.
Monte. O Everest, que fica na fronteira entre a China e o Nepal, é a montanha mais alta do mundo. Medir sua altura não é uma tarefa fácil e, de fato, a medição real tem sido uma fonte de controvérsia por centenas de anos. O processo de medição envolve o uso de triângulos e um ramo da matemática conhecido como trigonometria. Nesta seção, definiremos um novo grupo de funções conhecidas como funções trigonométricas e descobriremos como elas podem ser usadas para medir alturas, como as das montanhas mais altas.
Definimos anteriormente o seno e o cosseno de um ângulo em termos das coordenadas de um ponto no círculo unitário cruzado pelo lado terminal do ângulo:
\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]
Nesta seção, veremos outra maneira de definir funções trigonométricas usando propriedades de triângulos retos.
Usando triângulos retos para avaliar funções trigonométricas
Nas seções anteriores, usamos um círculo unitário para definir as funções trigonométricas. Nesta seção, estenderemos essas definições para que possamos aplicá-las aos triângulos retos. O valor da função seno ou cosseno de\(t\) é seu valor em\(t\) radianos. Primeiro, precisamos criar nosso triângulo reto. A figura\(\PageIndex{1}\) mostra um ponto em um círculo unitário de raio 1. Se derrubarmos um segmento de linha vertical do ponto\((x,y)\) para o eixo x, teremos um triângulo reto cujo lado vertical tem comprimento\(y\) e cujo lado horizontal tem comprimento\(x\). Podemos usar esse triângulo reto para redefinir seno, cosseno e outras funções trigonométricas como proporções dos lados de um triângulo reto.
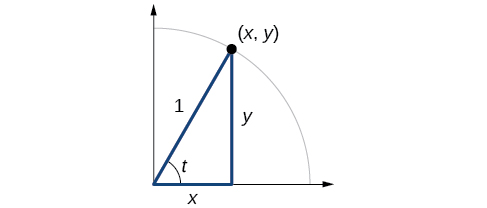
Nós sabemos
\[ \cos t= \frac{x}{1}=x \]
Da mesma forma, nós sabemos
\[ \sin t= \frac{y}{1}=y \]
Essas proporções ainda se aplicam aos lados de um triângulo reto quando nenhum círculo unitário está envolvido e quando o triângulo não está na posição padrão e não está sendo representado graficamente usando\((x,y)\) coordenadas. Para poder usar essas proporções livremente, daremos aos lados nomes mais gerais: Em vez de\(x\), chamaremos o lado entre o ângulo dado e o ângulo reto de lado adjacente ao ângulo\(t\). (Adjacente significa “próximo a”.) Em vez disso\(y\), chamaremos o lado mais distante do ângulo dado de lado oposto do ângulo\(t\). E, em vez disso\(1\), chamaremos o lado de um triângulo reto oposto ao ângulo reto de hipotenusa. Esses lados estão identificados na Figura\(\PageIndex{2}\).
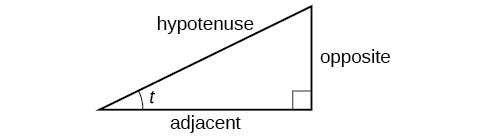
Compreendendo os relacionamentos do triângulo reto
Dado um triângulo reto com um ângulo agudo de\(t\),
\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]
Um mnemônico comum para lembrar essas relações é SohCahtoA, formado a partir das primeiras letras de “S”, a linha não é o oposto da hipotenusa, a cosena C é adjacente à hipotenusa, a tangente T é o oposto um adjacente.”
como: Dados os comprimentos laterais de um triângulo reto e um dos ângulos agudos, encontre o seno, o cosseno e a tangente desse ângulo
- Determine o seno como a razão entre o lado oposto e a hipotenusa.
- Determine o cosseno como a razão entre o lado adjacente e a hipotenusa.
- Determine a tangente é a razão entre o lado oposto e o lado adjacente.
Exemplo\(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle
Dado o triângulo mostrado na Figura\(\PageIndex{3}\), encontre o valor de\(\cos α\).
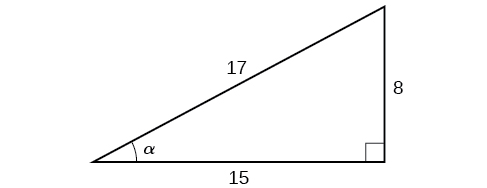
Solução
O lado adjacente ao ângulo é 15 e a hipotenusa do triângulo é 17, então via Equation\ ref {cosdef}:
\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]
Exercício\(\PageIndex{1}\)
Dado o triângulo mostrado na Figura\(\PageIndex{4}\), encontre o valor de\(\sin t\).
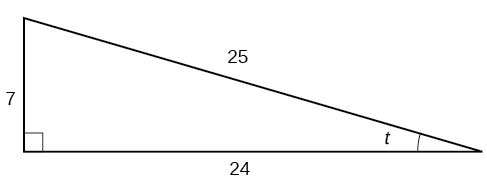
- Responda
-
\(\frac{7}{25}\)
Relacionando ângulos e suas funções
Ao trabalhar com triângulos retos, as mesmas regras se aplicam independentemente da orientação do triângulo. De fato, podemos avaliar as seis funções trigonométricas de qualquer um dos dois ângulos agudos no triângulo na Figura\(\PageIndex{5}\). O lado oposto a um ângulo agudo é o lado adjacente ao outro ângulo agudo e vice-versa.
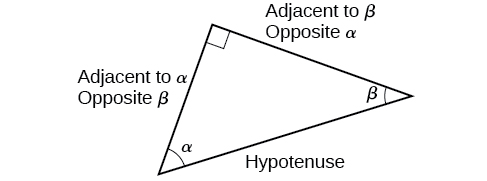
Seremos solicitados a encontrar todas as seis funções trigonométricas para um determinado ângulo em um triângulo. Nossa estratégia é encontrar primeiro o seno, o cosseno e a tangente dos ângulos. Então, podemos encontrar as outras funções trigonométricas facilmente porque sabemos que o recíproco do seno é cossecante, o recíproco do cosseno é secante e o recíproco da tangente é cotangente.
como: Dados os comprimentos laterais de um triângulo reto, avalie as seis funções trigonométricas de um dos ângulos agudos
- Se necessário, desenhe o triângulo direito e identifique o ângulo fornecido.
- Identifique o ângulo, o lado adjacente, o lado oposto ao ângulo e a hipotenusa do triângulo reto.
- Encontre a função necessária:
- seno como a proporção do lado oposto à hipotenusa
- cosseno como a proporção do lado adjacente à hipotenusa
- tangente como a razão entre o lado oposto e o lado adjacente
- secante como a proporção da hipotenusa para o lado adjacente
- cossecante como a proporção da hipotenusa para o lado oposto
- cotangente como a razão entre o lado adjacente e o lado oposto
Exemplo\(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position
Usando o triângulo mostrado na Figura\(\PageIndex{6}\),\( \sin α, \cos α, \tan α, \sec α, \csc α,\) avalie\( \cot α\) e.
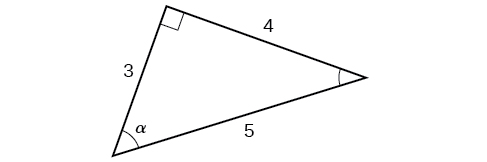
Solução
\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]
Exercício\(\PageIndex{2}\)
Usando o triângulo mostrado na Figura\(\PageIndex{7}\),\( \sin t, \cos t,\tan t, \sec t, \csc t,\) avalie\(\cot t\) e.
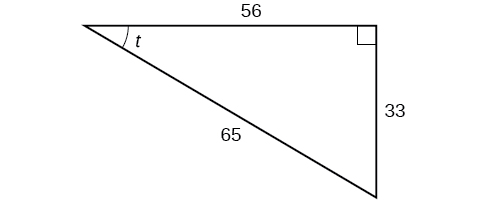
- Resposta
-
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]
Encontrando funções trigonométricas de ângulos especiais usando comprimentos laterais
Já discutimos as funções trigonométricas relacionadas aos ângulos especiais no círculo unitário. Agora, podemos usar essas relações para avaliar triângulos que contêm esses ângulos especiais. Fazemos isso porque, quando avaliamos os ângulos especiais em funções trigonométricas, eles têm valores relativamente amigáveis, valores que contêm nenhuma raiz quadrada ou apenas uma raiz quadrada na proporção. Portanto, esses são os ângulos frequentemente usados em problemas de matemática e ciências. Usaremos múltiplos de\(30°, 60°,\) e\(45°\), no entanto, lembremos que, ao lidar com triângulos retos, estamos limitados a ângulos entre eles\(0° \text{ and } 90°\).
Suponha que tenhamos um\(30°,60°,90°\) triângulo, que também pode ser descrito como um\(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triângulo. Os lados têm comprimentos na relação\(s,\sqrt{3}s,2s.\) Os lados de um\(45°,45°,90° \) triângulo, que também podem ser descritos como um\(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triângulo, têm comprimentos na relação.\(s,s,\sqrt{2}s.\) Essas relações são mostradas na Figura\(\PageIndex{8}\).
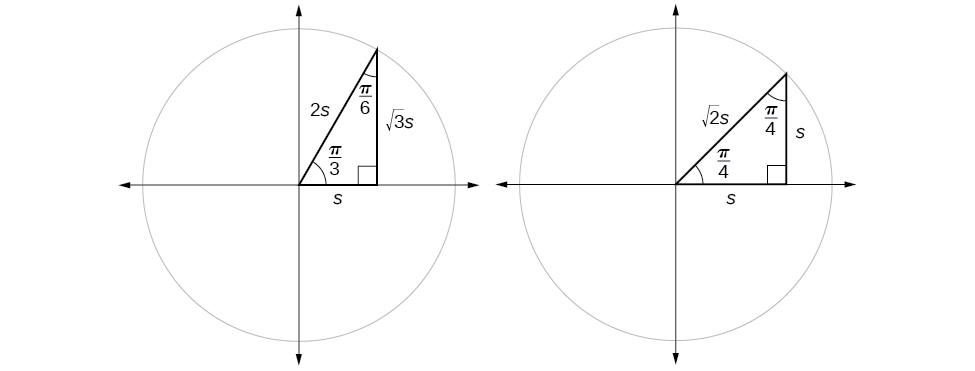
Podemos então usar as proporções dos comprimentos dos lados para avaliar as funções trigonométricas de ângulos especiais.
Dadas as funções trigonométricas de um ângulo especial, avalie usando comprimentos laterais.
- Use os comprimentos laterais mostrados na Figura\(\PageIndex{8}\) para o ângulo especial que você deseja avaliar.
- Use a proporção de comprimentos laterais apropriada para a função que você deseja avaliar.
Exemplo\(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths
Encontre o valor exato das funções trigonométricas de\(\frac{π}{3}\), usando comprimentos laterais.
Solução
\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]
Exercício\(\PageIndex{3}\)
Encontre o valor exato das funções trigonométricas do\(\frac{π}{4}\) uso de comprimentos laterais.
- Resposta
-
\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)
\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)
Usando a mesma função de complementos
Se observarmos mais de perto a relação entre o seno e o cosseno dos ângulos especiais em relação ao círculo unitário, notaremos um padrão. Em um triângulo reto com ângulos de\(\frac{π}{6}\) e\(\frac{π}{3}\), vemos que o seno de\(\frac{π}{3}\), ou seja\(\frac{\sqrt{3}}{2}\), também é o cosseno de\(\frac{π}{6}\), enquanto o seno de\(\frac{π}{6}\), ou seja, também\(\frac{1}{2},\) é o cosseno de\(\frac{π}{3}\) (Figura\(\PageIndex{9}\)).
\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]
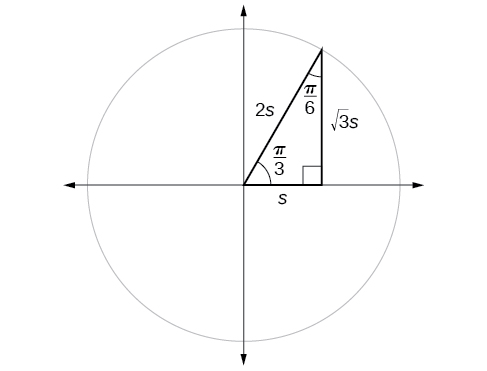
Esse resultado não deve ser surpreendente porque, como vemos na Figura\(\PageIndex{9}\), o lado oposto ao ângulo de também\(\frac{π}{3}\) é o lado adjacente a\(\frac{π}{6}\), então\(\sin (\frac{π}{3})\) e\(\cos (\frac{π}{6})\) são exatamente a mesma proporção dos mesmos dois lados,\(\sqrt{3} s\) e\(2s.\) similarmente,\( \cos (\frac{π}{3})\) e\( \sin (\frac{π}{6})\) também são a mesma proporção usando os mesmos dois lados,\(s\)\(2s\) e.
A inter-relação entre os senos e os cossenos de\(\frac{π}{6}\) e\(\frac{π}{3}\) também vale para os dois ângulos agudos em qualquer triângulo reto, pois em todos os casos, a proporção dos mesmos dois lados constituiria o seno de um ângulo e o cosseno do outro. Como os três ângulos de um triângulo se somam a π, e o ângulo reto é\(\frac{π}{2}\), os dois ângulos restantes também devem ser somados\(\frac{π}{2}\). Isso significa que um triângulo reto pode ser formado com quaisquer dois ângulos que se somam a\(\frac{π}{2}\) — em outras palavras, quaisquer dois ângulos complementares. Portanto, podemos declarar uma identidade cofuncional: se dois ângulos forem complementares, o seno de um é o cosseno do outro e vice-versa. Essa identidade é ilustrada na Figura\(\PageIndex{10}\).
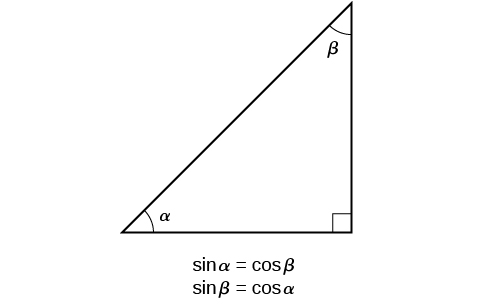
Usando essa identidade, podemos afirmar sem calcular, por exemplo, que o seno de\(\frac{π}{12}\) é igual ao cosseno de\(\frac{5π}{12}\), e que o seno de\(\frac{5π}{12}\) é igual ao cosseno de\(\frac{π}{12}\). Também podemos afirmar que se, para um determinado ângulo\(t, \cos t= \frac{5}{13},\), então\( \sin (\frac{π}{2}−t)=\frac{5}{13}\) também.
IDENTIDADES DE COFUNÇÃO
As identidades de cofunção em radianos estão listadas na Tabela\(\PageIndex{1}\).
| \( \cos t= \sin (\frac{π}{2}−t)\) | \( \sin t= \cos (\dfrac{π}{2}−t)\) |
| \( \tan t= \cot (\dfrac{π}{2}−t) \) | \( \cot t= \tan (\dfrac{π}{2}−t)\) |
| \( \sec t= \csc (\dfrac{π}{2}−t) \) | \( \csc t= \sec (\dfrac{π}{2}−t)\) |
como: Dado o seno e o cosseno de um ângulo, encontre o seno ou cosseno de seu complemento.
- Para encontrar o seno do ângulo complementar, encontre o cosseno do ângulo original.
- Para encontrar o cosseno do ângulo complementar, encontre o seno do ângulo original.
Exemplo\(\PageIndex{4}\): Using Cofunction Identities
Se\( \sin t = \frac{5}{12},\) encontrar\(( \cos \frac{π}{2}−t)\).
Solução
De acordo com as identidades de cofunção para seno e cosseno,
\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]
Então
\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]
Exercício\(\PageIndex{4}\)
Se\(\csc (\frac{π}{6})=2,\) encontrar\( \sec (\frac{π}{3}).\)
Solução
2
Usando funções trigonométricas
Em exemplos anteriores, avaliamos o seno e o cosseno em triângulos onde conhecíamos os três lados. Mas o verdadeiro poder da trigonometria do triângulo reto surge quando observamos triângulos nos quais conhecemos um ângulo, mas não conhecemos todos os lados.
como: Dado um triângulo reto, o comprimento de um lado e a medida de um ângulo agudo, encontre os lados restantes
- Para cada lado, selecione a função trigonométrica que tem o lado desconhecido como numerador ou denominador. O lado conhecido, por sua vez, será o denominador ou o numerador.
- Escreva uma equação definindo o valor da função do ângulo conhecido igual à razão dos lados correspondentes.
- Usando o valor da função trigonométrica e o comprimento do lado conhecido, resolva o comprimento do lado ausente.
Exemplo\(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios
Encontre os lados desconhecidos do triângulo na Figura\(\PageIndex{11}\).
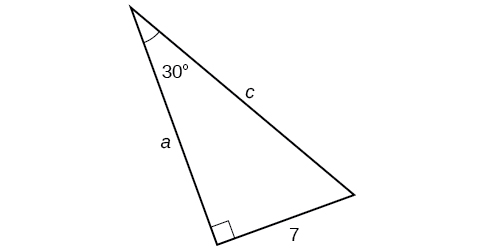
Solução
Conhecemos o ângulo e o lado oposto, então podemos usar a tangente para encontrar o lado adjacente.
\[ \tan (30°)= \dfrac{7}{a} \nonumber\]
Nós nos reorganizamos para resolver\(a\).
\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]
Podemos usar o seno para encontrar a hipotenusa.
\[ \sin (30°)= \dfrac{7}{c} \nonumber\]
Novamente, nós nos reorganizamos para resolver\(c\).
\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]
Exercício\(\PageIndex{5}\):
Um triângulo reto tem um ângulo\(\frac{π}{3}\) e uma hipotenusa de 20. Encontre os lados e o ângulo desconhecidos do triângulo.
- Resposta
-
\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\)o ângulo ausente é\(\frac{π}{6}\)
Usando trigonometria de triângulo reto para resolver problemas aplicados
A trigonometria do triângulo reto tem muitas aplicações práticas. Por exemplo, a capacidade de calcular os comprimentos dos lados de um triângulo torna possível encontrar a altura de um objeto alto sem subir até o topo ou precisar estender uma fita métrica ao longo de sua altura. Fazemos isso medindo a distância da base do objeto até um ponto no solo a alguma distância, onde podemos olhar para o topo do objeto alto em um ângulo. O ângulo de elevação de um objeto acima de um observador em relação ao observador é o ângulo entre a horizontal e a linha do objeto até o olho do observador. O triângulo reto que essa posição cria tem lados que representam a altura desconhecida, a distância medida da base e a linha de visão angular do solo até o topo do objeto. Sabendo a distância medida até a base do objeto e o ângulo da linha de visão, podemos usar funções trigonométricas para calcular a altura desconhecida. Da mesma forma, podemos formar um triângulo a partir do topo de um objeto alto olhando para baixo. O ângulo de depressão de um objeto abaixo de um observador em relação ao observador é o ângulo entre a horizontal e a linha do objeto até o olho do observador. Veja a Figura\(\PageIndex{12}\).
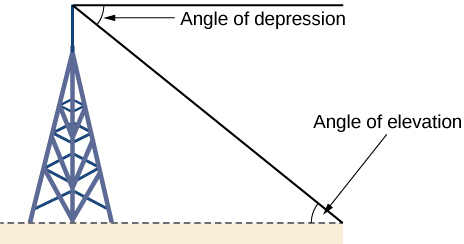
como: Dado um objeto alto, meça sua altura indiretamente
- Faça um esboço da situação do problema para acompanhar as informações conhecidas e desconhecidas.
- Estabeleça uma distância medida da base do objeto até um ponto em que a parte superior do objeto esteja claramente visível.
- Na outra extremidade da distância medida, olhe para a parte superior do objeto. Meça o ângulo que a linha de visão faz com a horizontal.
- Escreva uma equação relacionando a altura desconhecida, a distância medida e a tangente do ângulo da linha de visão.
- Resolva a equação para a altura desconhecida.
Exemplo\(\PageIndex{6}\): Measuring a Distance Indirectly
Para encontrar a altura de uma árvore, uma pessoa caminha até um ponto a 30 pés da base da árvore. Ela mede um ângulo de 57° 57° entre uma linha de visão até o topo da árvore e o solo, conforme mostrado na Figura\(\PageIndex{13}\). Encontre a altura da árvore.
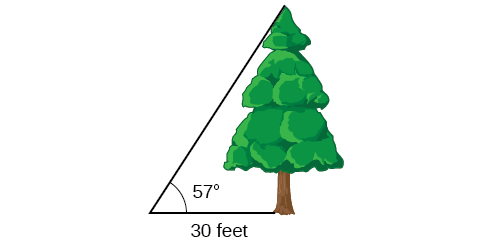
Solução
Sabemos que o ângulo de elevação é\(57°\) e o lado adjacente tem 30 pés de comprimento. O lado oposto é a altura desconhecida.
A função trigonométrica que relaciona o lado oposto a um ângulo e o lado adjacente ao ângulo é a tangente. Então, declararemos nossas informações em termos da tangente de\(57°\), deixando\(h\) ser a altura desconhecida.
\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]
A árvore tem aproximadamente 46 pés de altura.
Exercício\(\PageIndex{6}\):
Quanto tempo uma escada é necessária para alcançar o parapeito de uma janela 50 pés acima do solo se a escada estiver encostada no prédio fazendo um ângulo\(\frac{5π}{12}\) com o solo? Arredonde até o pé mais próximo.
- Resposta
-
Cerca de 52 pés
mídia:
Acesse esses recursos on-line para obter instruções e práticas adicionais com trigonometria do triângulo reto.
Visite este site para obter mais perguntas práticas do Learningpod.
Equações-chave
Identidades de cofunção
\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]
Conceitos-chave
- Podemos definir funções trigonométricas como proporções dos comprimentos laterais de um triângulo reto. Veja o exemplo.
- Os mesmos comprimentos laterais podem ser usados para avaliar as funções trigonométricas de qualquer ângulo agudo em um triângulo reto. Veja o exemplo.
- Podemos avaliar as funções trigonométricas de ângulos especiais, conhecendo os comprimentos laterais dos triângulos nos quais eles ocorrem. Veja o exemplo.
- Quaisquer dois ângulos complementares podem ser os dois ângulos agudos de um triângulo reto.
- Se dois ângulos são complementares, as identidades da cofunção afirmam que o seno de um é igual ao cosseno do outro e vice-versa. Veja o exemplo.
- Podemos usar funções trigonométricas de um ângulo para encontrar comprimentos laterais desconhecidos.
- Selecione a função trigonométrica que representa a razão entre o lado desconhecido e o lado conhecido. Veja o exemplo.
- A trigonometria do triângulo reto permite a medição de alturas e distâncias inacessíveis.
- A altura ou distância desconhecidas pode ser encontrada criando um triângulo reto no qual a altura ou distância desconhecida é um dos lados e outro lado e ângulo são conhecidos. Veja o exemplo.
Glossário
- lado adjacente
- em um triângulo reto, o lado entre um determinado ângulo e o ângulo reto
- ângulo de depressão
- o ângulo entre a horizontal e a linha do objeto até o olho do observador, supondo que o objeto esteja posicionado abaixo do observador
- ângulo de elevação
- o ângulo entre a horizontal e a linha do objeto até o olho do observador, supondo que o objeto esteja posicionado acima do observador
- lado oposto
- em um triângulo reto, o lado mais distante de um determinado ângulo
- hipotenusa
- o lado de um triângulo reto oposto ao ângulo reto


